Mathematica 在高等数学课程教学中的应用分析*

李守金

（潍坊科技学院 通识学院，山东 潍坊 262700）

引言

高等数学是高等院校许多专业开设的重要基础课程，是对学生的数学思想、数学文化、数学方法、数学素养以及数学能力进行综合培养和提高的关键课程，是学生学习后继数学课程和专业课程以及现代科学技术知识的基础。高等数学教学改革经过多年的探索和实践，取得了许多成效，但是在有的高等院校，高等数学作为一门重要的基础理论课程，基本上是沿用和继承固有体系，人才培养目标难以实现[1]。刘熙娟利用Mathematica 符号演算、数值计算、图形处理三种功能解决高等数学教学中遇到的实际问题，以改善高等数学课堂教学[2]。刘雄伟阐述了将Mathematica 融入高等数学教学，丰富高等数学的教学手段[3]。王绍恒提出将Mathematica 软件与大学数学整合可以改善课程教学硬件，提高课堂教学效率[4]。

一、Mathematica 软件简介

1988 年，由美国物理学家、数学家Stephen Wolfram 领导的团队开发了一款数学软件Mathematica。Mathematica 软件和 Wolfram 语言集成了科学计算领域先进的技术，Mathematica 很好地结合了数值和符号计算引擎、图形系统、编程语言、文本系统、和与其他应用程序的高级连接[5]，充分展示了科学计算的强大能力，在全球范围内推动着科技创新。Mathematica 软件从1988 年发布的 Mathematica1.0 到 2021 年 的 Mathematica 12.3，系统功能不断完善和增强，其应用更加快速、流畅和便捷。Mathematica 软件是数学和物理学领域的主要科研工具，在计算机科学、生命科学、信息科学、工程计算和金融等诸多领域，Mathematica软件也得到了广泛应用[6]1。Mathematica 作为高等数学实验教学重要软件之一，被广泛应用于高等数学实验教学中，用户创建并编辑笔记本文档，可以进行数值计算、符号或代数运算、图像处理、表格制作和编程等。高等数学大部分计算和作图都可以使用Mathematica 辅助完成，也可以直接使用wolfarm公司的专业数学计算网站[7]41。例如求，可以直接输入表达式，然后按Enter 键或点击“=”便会得到结果。如果不会输入命令，可以单击命令输入框下方的Examples 查看示例输入，或者直接输入Sin（x）2，网站自动提供求导结果及过程，还会得到与之相关的数学运算及其运算过程。

二、Mathematica 数值计算功能

在近二十年的算法开发中，Wolfram 语言建立一个数值计算的新层次。特别是它的许多高效原算法，自动算法选择的方法论，系统范围支持自动误差追踪和任意精度算法。Mathematica 中的数值分为整数、有理数、实数和复数四种类型。利用Mathematica 符号计算功能可以求出数学表达式的精确解，如果需要其近似解，可以使用数值计算N 命令计算任意指定精度的近似值，相反也可以对求得的近似值进行有理近似。N 命令格式如表1 所示[7]67。

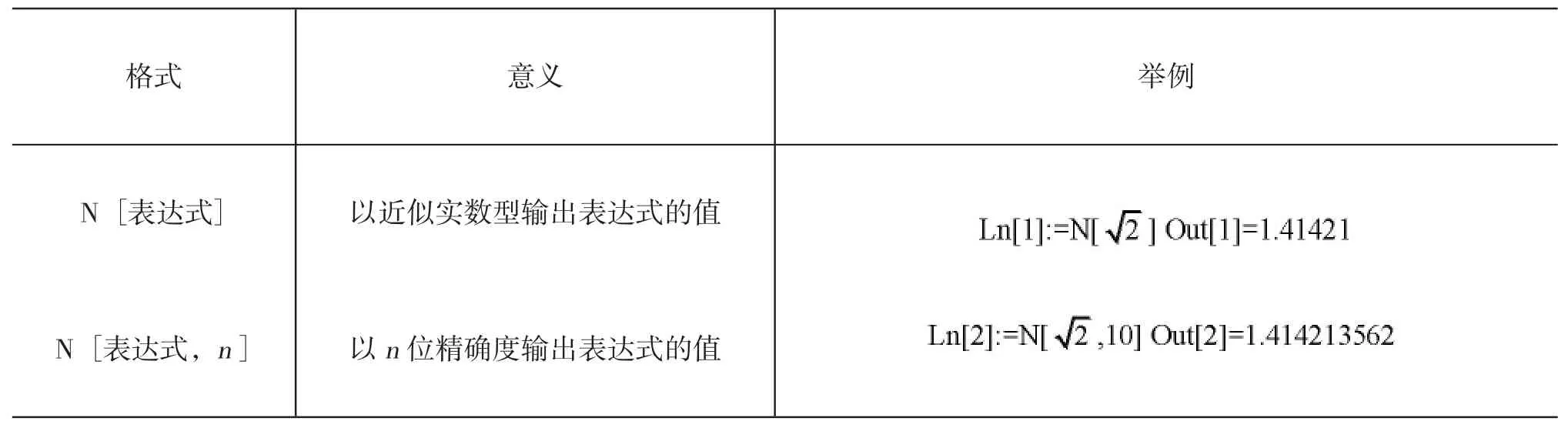
表1 Mathematica 数值计算的命令格式表

三、Mathematica 符号计算功能

微积分是学习高等数学的重点和难点内容，其中蕴含着各种变换和运算技巧。在微积分的学习过程中，学生只要掌握微积分的本质及其数学思想方法，对于微积分的许多问题都可以借助于Mathematica 的符号计算功能来实现。

（一） 求函数的极限

利用Mathematica 可以求解一元或多元函数极限，求一元函数极限的Mathematica 计算命令格式：Limit [f[x]，x→x0（或 x→∞）]，求多元函数极限的Mathematica 命令格式：Limit[f[x1，…，xn]，{x1→x1*，…，xn→xn*}]。

此例极限求解较为复杂，计算量较大，利用Mathematica 软件可以辅助计算。在Mathematica 笔记本文档输入极限计算命令：，同时按下Shift+Enter 运行便得出结果为。

也可以使用专业数学计算网站http://www.wolframalpha.com/，在输入框内输入上述极限计算命令后，按Enter 健或单击输入框右边的“=”按钮，即可显示出计算结果。点击网页上的“Step-bystep solution”按钮，会显示详细的解题步骤，核查计算步骤存在的问题，便于学习者自学。

（二） 求函数的导数或微分

利用Mathematica 可以求一元显函数的n阶导数或微分、隐函数及由参数方程所确定的函数的导数、多元显函数的n阶偏导数或偏微分、多元函数的全微分、符号函数的导数以及方向导数与梯度等。Mathematica 求函数导数或微分的计算命令格式，如表2 所示[7]106-108。

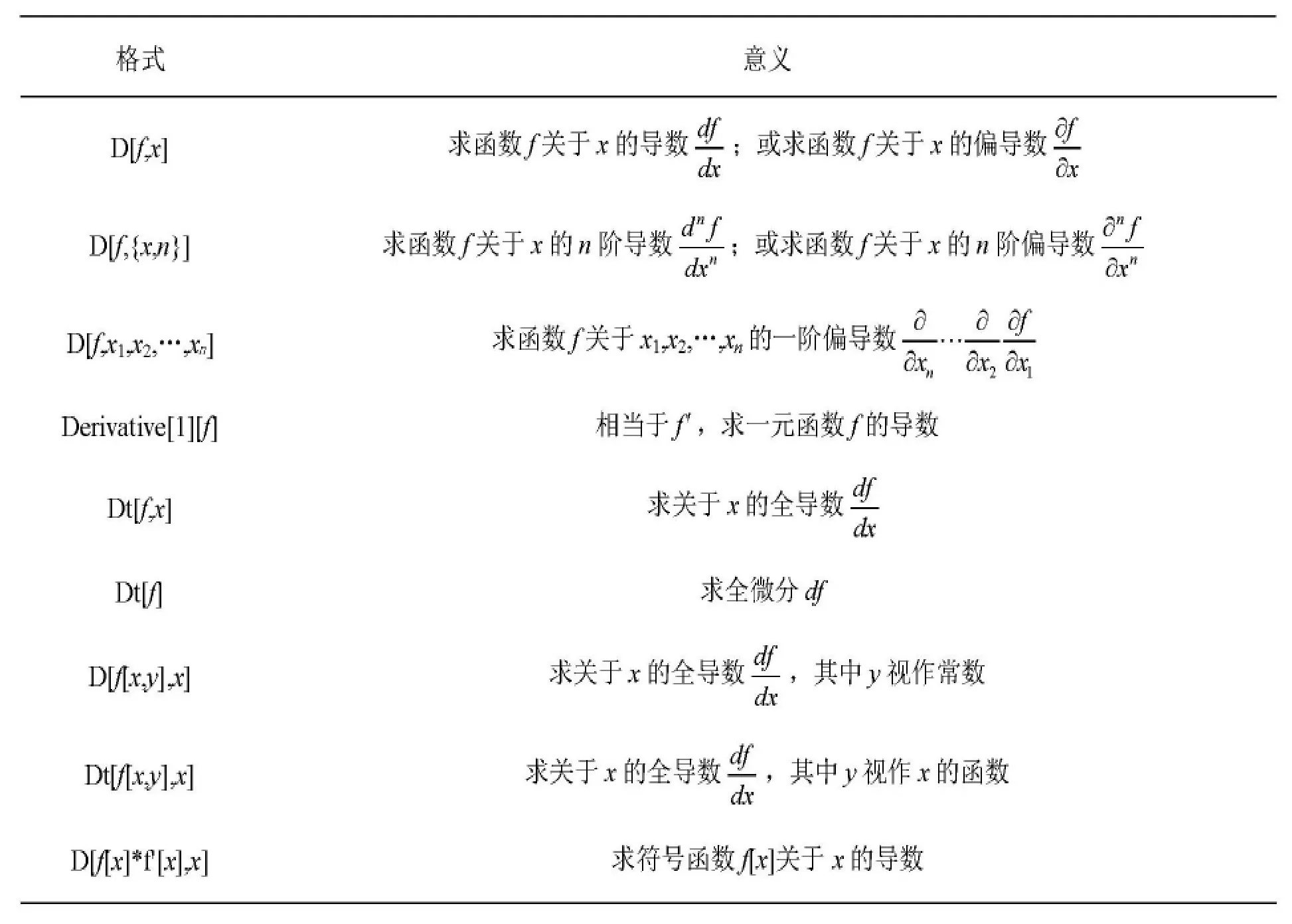
表2 Mathematica 中求函数的导数或微分的计算表

用 D[f[x，y]，x]求导时，若 y 是 x 的函数，要使用选择项NonConstants→{y}说明y 是非常量，若不注明，Mathematica 默认 y 为常量；用 Dt [f[x，y]，x]求导时，若y 是常量，要使用选择项Constants→{y}说明y 是常量，若不注明，Mathematica 默认y为非常量。

在Mathematica 笔记本输入命令：Dt[x+Sin[y/2]+Exp[yz]]，执行命令得到计算结果：Dt[x]+1/2Cos[y/2]Dt[y]+eyzDt[yz]，即。

（三） 求函数的积分

利用Mathematica 可以计算函数的不定积分、定积分、重积分；计算无穷区间上的广义积和无界函数的广义积分；计算曲线积分和曲面积分；进行积分变换；还可以求符号函数或抽象函数的不定积分。部分计算命令格式如下页表3 所示。

表3 Mathematica 中与积分相关的部分计算命令格式表

利用Mathematica 作出围成的闭区域，如图1所示。

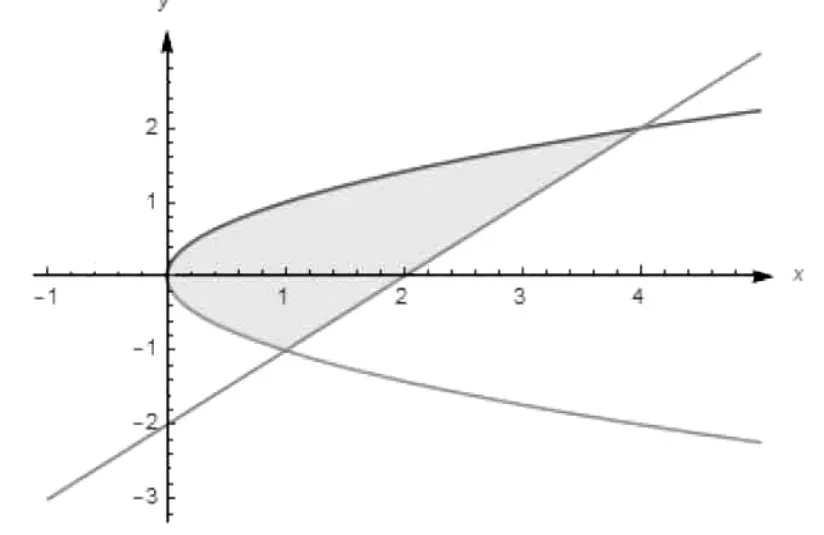
图1 抛物线y2=x 及直线y=x-2 围成的闭区域图

上图围成的闭区域可以看作Y 型区域：

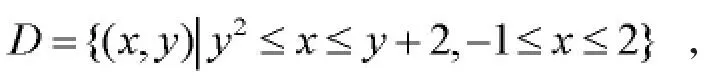
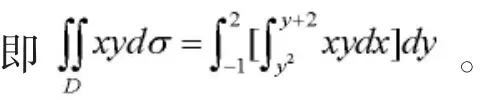
在Mathematica 笔记本输入命令：Integrate[x y，{y，-1，2}，{x，y^2，y+2}]，或者直接输入：，执行命令可以直接得到二重积分的结果为。注意命令中x 与y 的关系是乘积关系，x 与y 之间要么加空格，要么用“*”表示x 与y 的乘积。

该二重积分计算量较大，运用Mathematica 软件进行计算可以做到省时省力。

（四） 求解微分方程

利用Mathematica 可以求解常微分方程、偏微分方程、微分方程组、微分方程数值求解和微分方程组数值求解等，主要用到DSolve（求解微分方程）、NDSolve（数值求解微分方程组）、DSolve-Value（微分方程解） 三个命令，部分命令格式如下页表 4 所示[7]179-182。

表4 Mathematica 中DSolve 与NDSolve 的部分计算命令格式表

例4 微分方程y''-2y'+5y=0 的通解[8]341。

利用Mathematica 的DSolve 命令输入：DSolve[y''[x]-2y'[x]+5y[x]==0，y[x]，x]，执行命令输出运算结果：{{y[x]→exC2Cos[2 x]+exC1Sin[2 x]}}，即：y=ex（C2cos2x+C1sin2x）。

（五） 函数展成幂级数

利用Mathematica 可以进行级数的相关计算。利用Sum 可以求级数的和，利用Product 可以求级数的积，利用Series 可以将函数展成幂级数，利用FourierTrigSeries 可以将周期函数展成傅立叶级数，利用D 可以对幂级数进行逐项求导运算，利用Intergrate 可以对幂级数进行逐项积分运算等。

用Series 将函数f（x）在点x0展成幂级数命令格式：Series[f，{x，x0，n}]。

例5 将函数f（x）=ex展开成x的幂级数。

在Mathematica 笔记本输入命令：Series[Exp[x]，{x，0，7}]，执行命令后得到f（x）=ex在x=0 点直到 7次的幂级数展开式：。

利用Mathematica 还可以进行函数极值的搜索、向量的相关计算等。

四、Mathematica 图像处理功能

数学图像最早采用的是列表、描点、连线的方式作图，这样的手工作图仅能制作比较简单的、有规律可循的函数图像，对于比较复杂的函数图像，即使学习了高等数学中函数图形的描绘，在作图时也很困难，甚至无法实现。Mathematica 具有强大的图像处理功能，利用Mathematica 几乎可以实现所有高等数学的作图问题。Mathematica 可以绘制出精确精美的二维或三维彩色图像，可以绘制连续函数图像、离散函数图像、点图，可以绘制函数直角坐标方程、极坐标方程、参数方程所对应的图像，可以实现动画演示等。在高等数学教学中利用Mathematica 作图功能进行辅助教学，可以增强学生对抽象的数学概念和数学思想方法的直观认识。

（一） 二维图像作图

利用Mathematica 作出二维图像进行高等数学的直观教学，比如函数的性质、函数的连续性、函数的极限、函数的极值、微分方程的解等。

Mathematica 中绘制二维图像的内置函数有许多，其中 Plot 的格式为：Plot[f[x]，{x，a，b}，图形选项，表示的意义是画出函数f（x）在区间[a，b]上的图像。利用Plot 可以作出一个或者多个函数的二维图像。

在函数的极值的教学中，可以利用Mathematica 中Plot 作处函数的二维图形，根据函数极值的第二充分条件，利用Mathematica 相关命令可以标记函数的局部极值点。

输入以下命令：

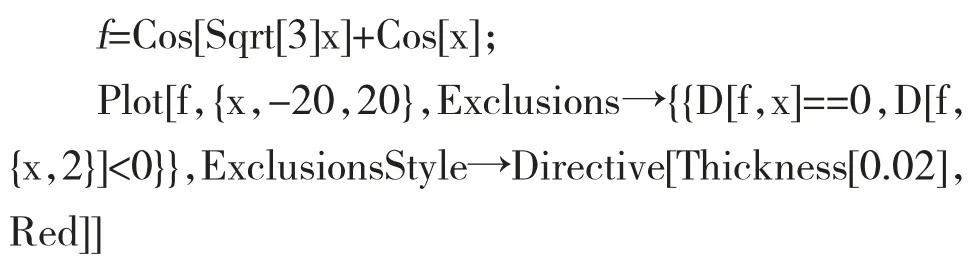
执行命令后得到所求函数的图像，如下页图2所示。

（二） 三维图像作图

利用Mathematica 可以作出既精美又直观的三维函数图像。在空间解析几何和重积分教学中，由于部分学生的空间思维能力的不强导致其难以掌握三维函数知识，因此，利用Mathematica 作出三维图像辅助教学就显得尤为重要。

使用Plot3D 绘制三维图像的基本命令格式：Plot3D[f，{x，a，b}，{y，c，d}，图像选项]或 Plot3D[{f1，f2…}，{x，a，b}，{y，c，d}，图像选项]。

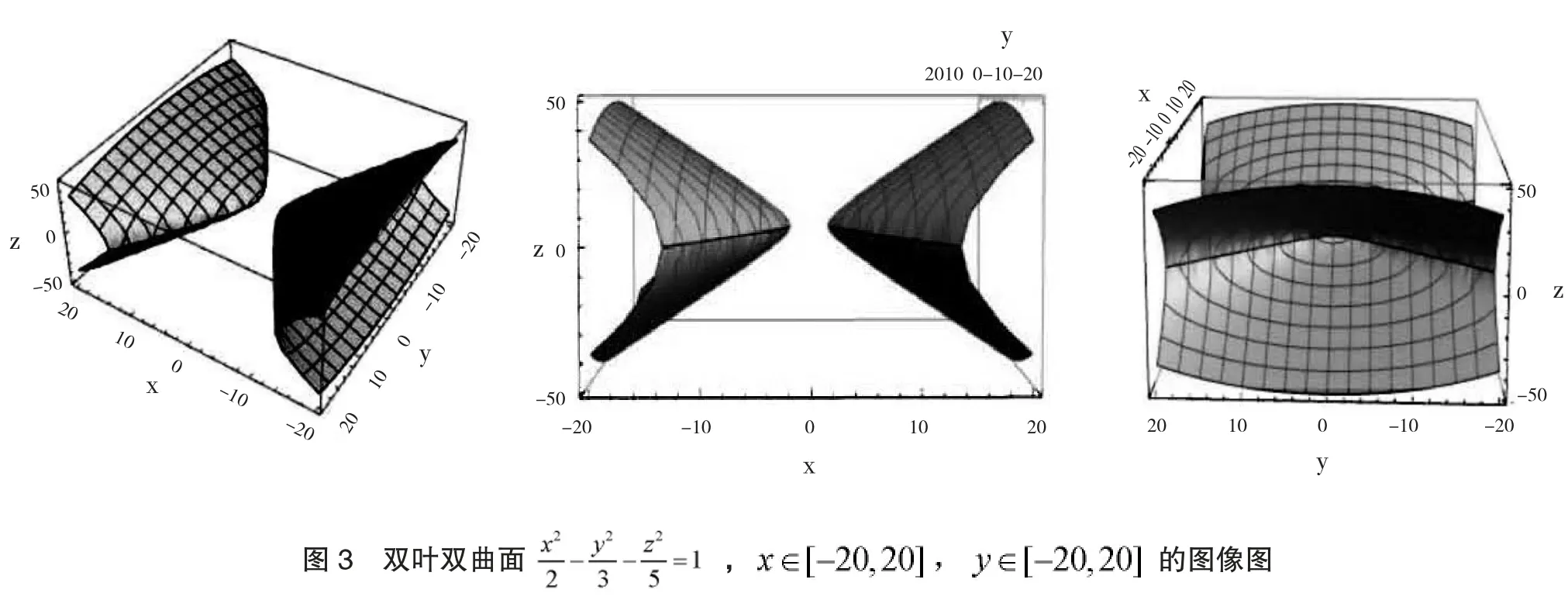
在Mathematica 笔记本输入命令：

Plot3D [{5*Sqrt [x^2/2^2-y^2/3^2-1]，-5*Sqrt[x^2/2^2-y^2/3^2-1]}， {x，-20，20}， {y，-20，20}，AxesLabel→{x，y，z}]

执行命令后得到双叶双曲面的三维图像，在Mathematica 笔记本文档中可以拖动进行旋转，从任意角度对三维图像进行观察，图3 所示即为其中的三幅图像。

五、Mathematica 表格制作功能

利用Mathematica 软件制作表格功能可以制作精美的表格，可以用于编写高质量的教材、设计精美的教案、进行高等数学辅助教学。利用Mathematica 创建一个函数，可以将表达式列表转换为格式良好的导数表。执行以下命令：

makeDerivativeTable[funs_List，x_]:=Grid[Prepend[Transpose [{funs，D [funs，x]}]，Style [#，FontWeight →Bold]&/@{HoldForm[f[x]]，HoldForm[f'[x]]}]，Grid options+//TraditionalForm;

makeDerivativeTable[{Sin[x]，Cos[x]，Tan[x]，Arc-Sin[x]，ArcCos[x]，ArcTan[x]}，x]，可以制作出三角函数导数表，如表5 所示。

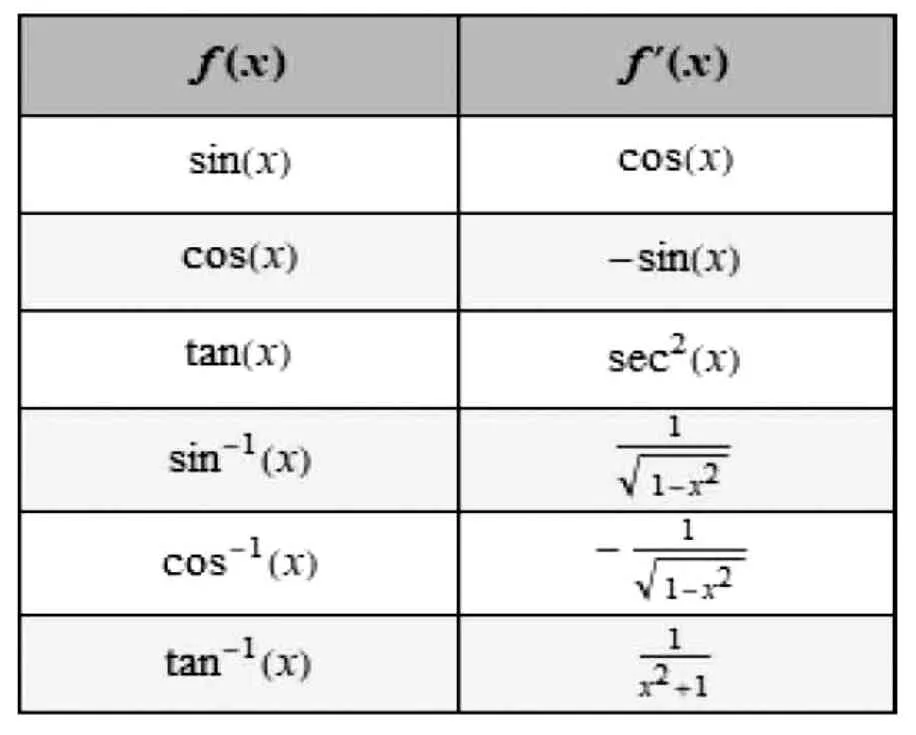
表5 利用Mathematica 制作的三角函数导数表

六、结语

Mathematica 作为被广泛运用的数学软件[9]，具有内容丰富、功能强大、界面友好、使用简单等优点。Mathematica 所处理的内容十分丰富，涵盖了数学应用的许多分支，如微积分、微分方程、线性代数、复变函数、概率与统计等，是进行数学研究及计算的有力工具[10]。利用Mathematica 数值计算功能可以进行众多数学表达式的精确值求解，也可以计算任意指定精度的近似值，可以弥补人类计算能力的不足。利用Mathematica 符号演算功能可以进行逻辑严密的数学推导，适合于进行课堂教学，因此，其为高等数学教学提供了强有力的支撑。Mathematica 具有强大的绘图功能，可以绘制出各种精美的平面或空间彩色图形，还可以实现图像的动画效果，弥补了学生空间想象能力和图像动态想象能力的不足，提高了图形的视觉效果，增加了学生对有关数学概念或方法的感性认识。鉴于Mathematica 精美图与表的制作功能，可以用于编写教材。基于Mathematica 软件学数学、做数学，能够把数学学习变得更有趣，可以提高学生学习数学的兴趣，培养学生的创新精神和数学素养。利用Mathematica 辅助高等数学的教与学，可以弥补传统教学方法的不足，从而提高教学质量。