三轴微振动实时测量技术研究
2022-02-05余才志孙长库
余才志,李 岳,王 鹏,孙长库
(天津大学精密仪器与光电子工程学院,天津 300072)
目前各个领域的加工生产过程均向着高、精、尖方向发展,微振动对生产环节的干扰成为滞约产业精密化发展的重要问题[1]。尤其是各类微电子、半导体、精密仪器等电子工业厂房中的精密设备对微振动的要求极为严苛,如在国标文件GB51076-2015 中规定:5 nm 制程生产线中的光刻设备和刻蚀设备在1 Hz~100 Hz 频段内的容许振动速度值仅为1.60 μm/s[2]。国内微振动测量与评估大多使用国外进口设备,如高广运等使用Micromed 公司的TROMINO 地脉动仪实现厂房微振动特性评估[3];刘维宁等使用朗斯公司的LC0130T 加速度传感器和LC0205-8 信号处理单元评估交通振动对古建筑的影响[4]。
电子工业厂房的环境微振动评价中,振动位移和速度是关键指标之一,如广泛应用于微电子生产领域的环境微振动评价标准——VC 振动标准采用振动速度的均方根值(RMS)作为评价指标[5]。在振动测试中,考虑到传感器参数指标、安装等实际问题,通常采用加速度传感器直接获取振动加速度信号,而后通过加速度和速度、位移之间的微分积分关系求解振动速度和位移。但由于原始加速度信号往往混叠有多种类型的噪声,导致经过积分得到的速度和位移包含严重的漂移和趋势项误差[6-7]。如何在提取并抑制趋势项误差的同时克服积分后信号漂移问题是积分算法的一个重要研究方向。
包含去噪算法的积分方法可分为两类:时域法和频域法。通过曲线拟合的方法对基线漂移曲线进行预测和补偿是时域法中抑制噪声干扰的一个重要技术手段[8]。同理,还可通过联立动力学方程构建误差最小化模型,达到抑制噪声的目的,如基于反问题求解的显式差分法[9]、基于Taylor 展开的显式积分法[10]等方法。但在进一步研究中发现,当加速度信号中混叠复杂噪声时,采用时域去噪方法效果并不理想[11],因此在工程实际中主要采用的是频域去噪算法,其中以频率截止算法、低频衰减算法和有效频段算法较为典型。
由于趋势项误差多呈现为低频、缓慢变化的信号,频率截止算法[12]和低频衰减算法[13]均是通过选定趋势项误差上限频率,进而将零频率到该上限频率之间的频率信息进行置零(频率截止)或衰减抑制(低频衰减)。这两种算法针对趋势项误差均有显著去噪效果,但对随机分布在其他频段的噪声处理效果并不理想,有效频段算法可以较好地解决这一问题。有效频段算法[14]假设频谱曲线中主频附近频段的频谱曲线符合高斯分布,进而利用高斯曲线拟合该部分频谱曲线,根据三倍标准差原则确定主频有效频段范围,从而达到去噪效果。
本文针对电子工业厂房中振动敏感区域微振动测量问题,设计并研制了三轴微振动实时测量系统,对振动敏感区域的微振动进行准确测量,指导隔振设计;针对趋势项误差和随机噪声干扰微振动测量的问题,提出一种非对称广义高斯曲线拟合分频段积分算法,有效抑制趋势项误差和随机噪声的干扰,对非对称加速度频谱有更好的积分精度和抗噪性能。
1 三轴微振动实时测量系统设计
三轴微振动实时测量系统示意图如图1 所示。针对微振动幅值较低且主要能量集中于低频段的特点,选用三个单轴向的731A 加速度传感器组成三轴向传感模块,传感器主要参数如表1 所示。

图1 微振动测量系统

表1 加速度传感器主要参数
由于微振动信号幅值较低,其加速度峰峰值一般在200 μgn左右,参考表1 提供的传感器灵敏度可知,传感器的输出电压峰峰值在毫伏左右。因此本文设计了由滤波电路、有源放大电路和继电器等部分组成的信号调理模块,其中继电器可由AD 芯片的IO 管脚控制开闭,用于在外部环境振动过大时切断与后续数字电路部分的连接,防止电路损坏。数字电路部分使用FPGA 完成三通道AD 转换控制,实现各通道同步采集,提高测量系统实时性。测量系统可以对0.5 Hz~200 Hz 频率范围内的微振动信号实现准确测量。
但在使用激光多普勒测振仪对测量系统进行校准实验时发现,测量信号受到放大电路及外部电源引入的噪声干扰,呈现为随机分布于测量频段范围内的噪声,如图2 所示。为了解决原始加速度信号受噪声干扰的问题,本文提出了一种非对称广义高斯曲线拟合分频段积分算法,应用于微振动测量系统中,完成对微振动信号的准确测量和等级评估。

图2 受噪声干扰的微振动原始信号
2 非对称广义高斯曲线拟合分频段积分算法
2.1 加速度频谱峰值区域分割
为了满足测量系统的实时性,在对加速度频谱峰值区域进行曲线拟合之前,首先要完成对峰值区域的自适应识别与分割。峰值区域识别有很多种方法,如基于K-S 检验的寻峰算法[15]、曲线拟合算法[16]等。本文考虑环境微振动信号所含的噪声特性,综合已有寻峰算法思路和测量系统实时性需求,采用基于希尔伯特变换的峰值区域分割算法。
希尔伯特变换能够有效抑制低幅值波动噪声的干扰,可以避免原始加速度频谱曲线中“毛刺”和“假峰”对寻峰算法的影响[17]。假设加速度时域信号经过FFT 得到加速度频谱信号,其希尔伯特变换为:

该变换还可表示为卷积形式:

上式可联立傅里叶变换进行简化计算,降低了算法复杂度,使其更适用于实时测量系统。

图3 加速度频谱希尔伯特变换效果图
设一帧实测加速度时域信号a(t)对应频谱为A(f),经由希尔伯特变换可知其包含n个峰值,其对应频率依次为f1,f2,…,fn。如此可将加速度频谱分割为如公式(3)所示的n段峰值区域。

式中:Δfi为希尔伯特变换后每个峰值所对应的两个突变极点之间的频率差;γ为区域占比系数,用于划分峰值区域的宽度。
为了便于后续分析,将n段峰值区域的振动幅值和频段分别进行归一化处理得到归一化后的峰值区域,其中
2.2 加速度频谱峰值区域曲线形态假设
为了更好的对非对称峰值频谱形态进行拟合,引入非对称广义高斯曲线(Asymmetric Generalized Gaussian Distribution,AGGD)[18],对n段峰值区域的归一化频谱分别进行形态假设:

式中:i=1,2,…,n;为每个峰值区域频段内的归一化频率;α为控制曲线“形状”的形状参数;li和ri分别为控制曲线左右扩散程度的左半径尺度参数和右半径尺度参数;max()表示归一化频谱中的峰值。其在不同参数设置下的曲线形式如图4 所示。
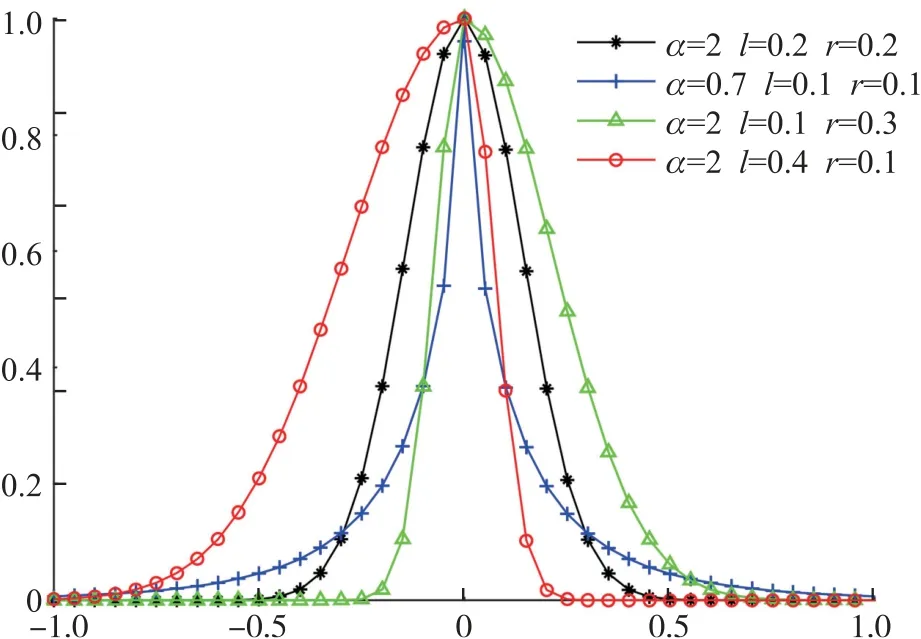
图4 不同参数设置下非对称广义高斯曲线
在非对称广义高斯曲线(式(4))中,形状参数控制着曲线的“形态”。左、右半径尺度参数与左、右瓣样本的标准差的关系如式(5)所示。

式中:Nl和Nr分别为左、右瓣样本对应的样本数量。频率修正标准差是将归一化峰值频段的频率定义为样本,其对应的归一化幅值定义为频率在整个频段中所占权重。
2.3 非对称广义高斯曲线拟合参数估计
非对称广义高斯曲线三个参数的取值直接决定了本文所提出的积分算法的去噪效果。采用二阶统计量估计法来确定参数取值。定义样本的一阶绝对值矩为,定义样本的二阶原点矩为
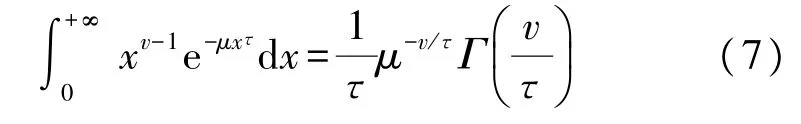
通过式(7)所示的积分关系可推导出一阶绝对值矩、二阶原点矩与参数αi,li,ri之间的关系。



观察函数q(αi)的形式可知其反函数的解析式较难求解,故可采用双曲线函数进行数值拟合的方法来简化估计其解析式。由最小二乘法求得用于拟合反函数的双曲线函数解析式为:

故由式(5)、式(6)和式(13)可得左、右半径尺度参数的估计值如式(15)所示。
2.4 积分频段确定
依据本文2.3 节中提出的非对称广义高斯曲线拟合参数估计方法,其操作实例例如图5 所示。图5显示了经过自适应加速度频谱峰值区域分割得到的某段归一化频段带噪加速度离散信号和拟合得到的非对称广义高斯频谱曲线。
积分频段的确定方法如图5 所示,定义积分频段求解公式为:


图5 归一化频段内的频谱曲线拟合示意图
式中:c为积分频段抑制系数,一般根据主频信号形态在0.05~0.5%的范围内选取。该式经过整理可得积分频段的上下限频率为:
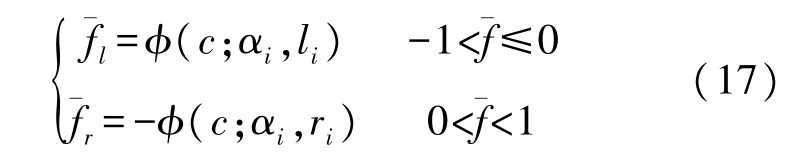
式中:ϕ(·)为包含参数li、ri和αi的关于参数c单调递减的函数。因此参数c取值越大,积分频段范围越小。
与之对应的实际积分频段为:

本文提出的非对称广义高斯曲线拟合分频段积分算法的滤噪流程如图6 所示。本文提出的算法利用非对称广义高斯曲线拟合自动识别划分最佳积分频段,抑制了主要频率之外的测量噪声干扰。相比于采用对称高斯曲线拟合去噪算法,本文提出的算法针对非对称加速度频谱进行优化,适用性更强。

图6 积分算法流程图
3 实验
3.1 数值算例仿真实验
如图7 所示为电子工业厂房中洁净室常见建筑结构——格构梁结构的有限元仿真模型。

图7 格构梁结构模型
考虑工程实际情况,选取筏板中心位置作为振源位置,在振源位置处施加竖直方向的多频简谐激励和白噪声激励。电子工业厂房中能够影响高精密设备正常运行的振动主要有0~1 Hz 的地面振动、4 Hz~10 Hz 由空调房、电梯房引起的微振动和15 Hz~25 Hz 的房屋骨架、底板振动[19],因此为了模拟电子厂房实际振动响应,选取对应频段的激励组成多频简谐振动激励。选取格构梁中心位置作为测点位置,利用有限元分析仿真振源对测点位置振动情况影响,求解出测点位置的加速度、速度作为真实值参考。在真实加速度中添加1%、5%、10%…35%的白噪声作为测量加速度。利用本文提出的非对称广义高斯曲线拟合分频段积分算法对测量加速度进行积分求解。作为对比,同时采用频率截止法和对称高斯曲线拟合去噪算法对测量加速度进行积分求解,考察不同算法的去噪效果和积分精度。采用式(19)定义的平均相对误差δErs作为积分精度的评估指标。

式中:vreal是由有限元分析得到的测点位置处的振动速度真实值参考;v是由各个算法得到的重建振动速度。
本文算法与对称高斯曲线拟合法、频率截止法的积分精度对比如图8 所示。从图中可以看出,本文提出的算法在对不同噪声能量水平下的测量加速度进行积分得到的振动速度平均相对误差较低,积分精度更高;在噪声相对能量占比30%以下时,对称高斯曲线拟合法和本文算法的平均误差均在1%~2%之间,积分精度较好;在噪声相对能量占比为30%时,对称高斯曲线拟合法的平均相对误差上升到2%以上,而本文算法的平均相对误差在2%以下,依然有较好的积分精度。

图8 不同噪声能量下各算法误差
图9 和图10 分别给出了在噪声相对能量占比为30%时,利用三种算法去噪后的加速度频谱对比,积分后的振动速度时程对比。

图9 30%噪声能量下各算法去噪后加速度频谱对比

图10 30%噪声能量下各算法积分后速度时程对比
从图中可以看出:
①频率截止法并不适用于本文设计的数值仿真算例。为了模拟建筑结构实际微振动响应,本文采用的数值仿真算例低频目标频率较低,因此频率截止法设置的截止频率较低导致大部分噪声没有得到有效抑制,去噪效果较差。
②采用对称高斯曲线拟合的去噪算法完成了对主频信号与噪声信号的分离,但是由于其拟合曲线是对称的,在对非对称主频信号进行拟合时不可避免的导致拟合高斯曲线半径变大,从而引入更多的主频外噪声影响。本文提出的算法在应对非对称主频信号时采用同样非对称的广义高斯拟合曲线,根据主频信号的形态自动调整拟合曲线的左右半径,从而达到更好的去噪效果。
图11 给出了本文算法的积分误差在不同噪声能量下受抑制系数c取值的影响。在不同的噪声水平下,算法的计算精度基本上与抑制系数c满足单调关系;同时,抑制系数c取值为0.01~0.05 时,对算法的计算精度影响几乎相同。因此为了尽可能多的保留原有信息,仿真实验过程中抑制系数的取值均为0.05。除此之外,图11 的结果也表明:不同的噪声水平对抑制系数的取值没有影响。

图11 不同噪声能量下抑制系数取值对积分误差的影响
3.2 校准实验
为了验证测量系统和算法能否解决在校准实验中振动信号受噪声干扰的问题,利用标准振动台对测量系统中的传感模块进行激振使其输出标准正弦振动信号,并与激光多普勒测振仪的输出信号进行对比。实验实施图如图12 所示,标准振动台和激光多普勒测振仪主要参数如表2 和表3 所示。

表2 标准振动台主要参数

表3 激光多普勒测振仪主要参数(量程最小档位)

图12 校准实验实施图
由于激光多普勒测振仪输出信号采样频率与本文搭建的测量系统的信号采样频率不同,因此采用振动速度峰峰值平均误差作为去噪效果评判标准。由图13 和表4 显示的结果可以看出:

表4 去噪前后信号对比
①去噪前加速度频谱中除了主频信号之外还夹杂着随机分布于整个频谱范围内的噪声;尤其分布于主频信号附近的噪声幅值随着临近主频噪声频率而不断增大,如图13 所示。由原始信号加速度时域波形明显叠加着多种频率噪声干扰,速度峰峰值相对误差达到35.11%,严重影响测量系统的校准。

图13 去噪前后效果对比图
②通过对称高斯拟合算法和本文提出的算法进行去噪处理后的加速度频谱仅保留主频有效信号,噪声得到有效抑制。去噪前后经过积分得到的速度信号与激光多普勒测振仪得到的标准速度信号进行比对,使用本文算法进行去噪后的振动速度峰峰值误差相较于去噪前从35.11%下降至3.43%。
因此,将本文提出的非对称广义高斯曲线拟合分频段积分算法应用于微振动测量系统,很好地解决了测量噪声对校准实验的干扰问题。
4 总结
本文设计了用于电子工业厂房中振动敏感区域微振动测量的三轴微振动实时测量系统。针对微振动测量中低频趋势项误差和测量噪声干扰等问题,本文提出了一种非对称广义高斯曲线拟合分频段积分算法。该算法通过峰值区域分割自动定位频谱峰值区域,并利用非对称广义高斯曲线对峰值区域进行拟合,实现主频信息与次频信息及其上的测量噪声的分离,从而提高了积分精度和去噪性能。通过数值仿真算例,与频率截止法和对称高斯曲线拟合法进行对比分析,验证了本文提出的算法在应对非对称加速度频谱时的优越性;在测量系统校准实验中应用本文提出的算法,振动速度峰峰值误差从35.11%降低到了3.43%,解决了噪声干扰问题。该系统和算法可以实现对环境微振动进行实时准确的等级评估,指导隔振设计,对半导体生产线的科学设计和半导体产品的安全生产有重要意义。
