偏心率对颗粒介质次生各向异性的影响

周小文 许衍彬 赵仕威 陈昊 张昌辉

（华南理工大学亚热带建筑科学国家重点实验室∥华南岩土研究院，广东 广州 510640）

颗粒介质于岩土水利工程中应用较为广泛，常见于尾矿砂蓄积、大砂袋吹填、路基碎石铺设等［1-3］。然而，颗粒介质在细观上呈现出较宏观尺度更为明显的不连续性与组构各向异性，而其宏观层面物理力学特性的各向异性与其细观组构各向异性密不可分［4-5］，因此对各向异性的细观尺度研究具有重要意义。Casagrande［6］依据各向异性成因将其划分为原生各向异性和次生各向异性，原生各向异性源于颗粒集合体在天然沉积过程中因颗粒级配及颗粒形状导致的颗粒排列及接触的空间差异，而次生各向异性则源于颗粒在外部荷载扰动下的原生组构重新排列。Oda等［7］进一步地基于颗粒集合体的接触法向与接触力等细观组构张量给出了各向异性的定量表征，为从细观尺度解析颗粒介质诸多典型宏观力学现象（例如，挤压膨胀效应［8］、粮仓效应［9］、拱效应［10］、剪切带［11-12］及液化［13-14］等）的机理提供了可能；Rothenburg等［15］提出的应力-力-组构（SFF）关系即是从细观尺度出发研究颗粒介质宏观力学特性的典型代表，相关研究表明了颗粒介质宏观抗剪强度与细观组构各向异性之间密切的跨尺度联系。因此，为进一步揭示颗粒介质宏观力学现象的细观机理，基于组构各向异性的SFF关系进行跨尺度研究即为一条重要途径。

对颗粒形状特征进行准确描述是进行细观尺度研究的基础。然而由于建模方便及计算效率限制，既有颗粒材料组构各向异性的研究多基于二维模拟或形状规则颗粒（如理想的圆盘或球颗粒［16-19］）。但是，理想球颗粒与自然界中真实复杂颗粒形状相差甚远，前者不仅颗粒间接触形式单一，且由于法向接触力指向颗粒质心而无法考虑真实颗粒间的转动阻抗与咬合互锁等作用。导致外部荷载驱动下颗粒旋转自由度增大，进而颗粒定向排列现象减弱且组构空间分布趋向均匀，颗粒分布随机性增强，所以细观组构各向异性及其影响下的力学特性无法被真实地揭示［20］。基于此，为考虑颗粒形状特征的影响并保证计算效率，有学者［21-22］尝试在球颗粒中引入转动阻抗模型来间接考虑颗粒形状特征的影响，但此类折中表征方式在模拟组构各向异性演化方面尚有不足［23-24］。因此，直接采用趋真非球颗粒来反映颗粒形状特征的影响并结合更为丰富的非球颗粒组构各向异性表征方式进行研究是一条更具科学意义的途径。非球颗粒往往具有颗粒长轴并存在长轴排列优先性，因此有学者［25］通过颗粒长轴分布方向性来额外表征组构各向异性。此外，由于非球颗粒间接触法向与支向量不相重合，且二者夹角随颗粒不规则性增大而增大［26］（此种不重合也产生了额外力矩［27］），因此非球颗粒集合体中支向量对几何各向异性奉献较大，Ouadfel等［28］针对椭球颗粒额外引进支向量表征组构各向异性。

鉴于上文所述，颗粒形状特征对颗粒介质组构各向异性的演化起着重要作用，趋真非球颗粒组构各向异性的研究也逐渐增多。比如，由细观组构各向异性引起的典型宏观力学现象受颗粒形状的影响逐渐被关注，诸如拱效应［29］、剪切带［30］、液化［31-32］等；应力-力-组构（SFF）关系理论的适用性也先后被多种趋真非球颗粒所验证，如椭球［28］、超级球［33］、超级椭球［24］、多面体［31］及球簇［34］等。同时较多学者基于上述组构各向异性的表征方式，致力于颗粒形状特征对次生细观各向异性的影响研究。譬如，有学者采用准球多面体［35-36］、准球球簇［37］以及超级球［33］来探究棱角度、球度对次生细观各向异性演化的影响。亦有学者探究长细比对次生细观各向异性演化的影响，此方面不乏椭球［26，38］、超级椭球［24，39］、延长多面体［40］、RCR颗粒［41］、球簇［42-43］等非球颗粒。但作者注意到，以上研究将长细比与棱角度等指标糅合起来，以致于难以精准探究单一形态指标对组构各向异性的影响。并且，在已有的相关文献中，未能找到有学者对颗粒偏心不对称进行量化与研究。而实际上偏心率越大，法向接触力偏离质心愈发显著，产生了额外的绕质心转动阻抗。继而，颗粒之间互锁咬合效应随之增大，颗粒旋转自由度也随之减小。因此，组构各向异性和宏观抗剪强度受到影响。对此，本研究提出偏心率量化颗粒主轴不对称的程度，一定程度上完善了颗粒形态特征的量化指标体系。并继而尝试基于非对称扩展超级椭球进行了不同偏心率的颗粒介质趋真建模，以期探究偏心率对颗粒介质次生细观各向异性演化的影响，为进一步揭示众多力学现象的细观机理并建立考虑颗粒形状特征的颗粒材料各向异性细观本构提供参考。

1 离散元模型建立

1.1 趋真颗粒形状模型

超椭球在局部笛卡尔坐标系下方程［44］为

式中：rx、ry、rz分别代表x、y、z轴的半主轴长；ε1、ε2衡量颗粒表面棱角度。

超椭球虽可刻画自然界中80%的颗粒形态特征，但仍不能定量刻画现实颗粒的偏心现象。为对颗粒偏心率的变化进行定量描述，笔者所在团队在超级椭球模型的基础上开发了扩展超级椭球［45］趋真颗粒模型，如图1所示。其由8个不同形状超级椭球的八分体在保证表面连续、光滑的前提下组成，在表征颗粒形状特征上相比其他非球颗粒具有更高广度，且其接触检测算法的鲁棒性和效率性也已通过堆积试验（动态）和三轴试验（准静态）得以验证［45］。

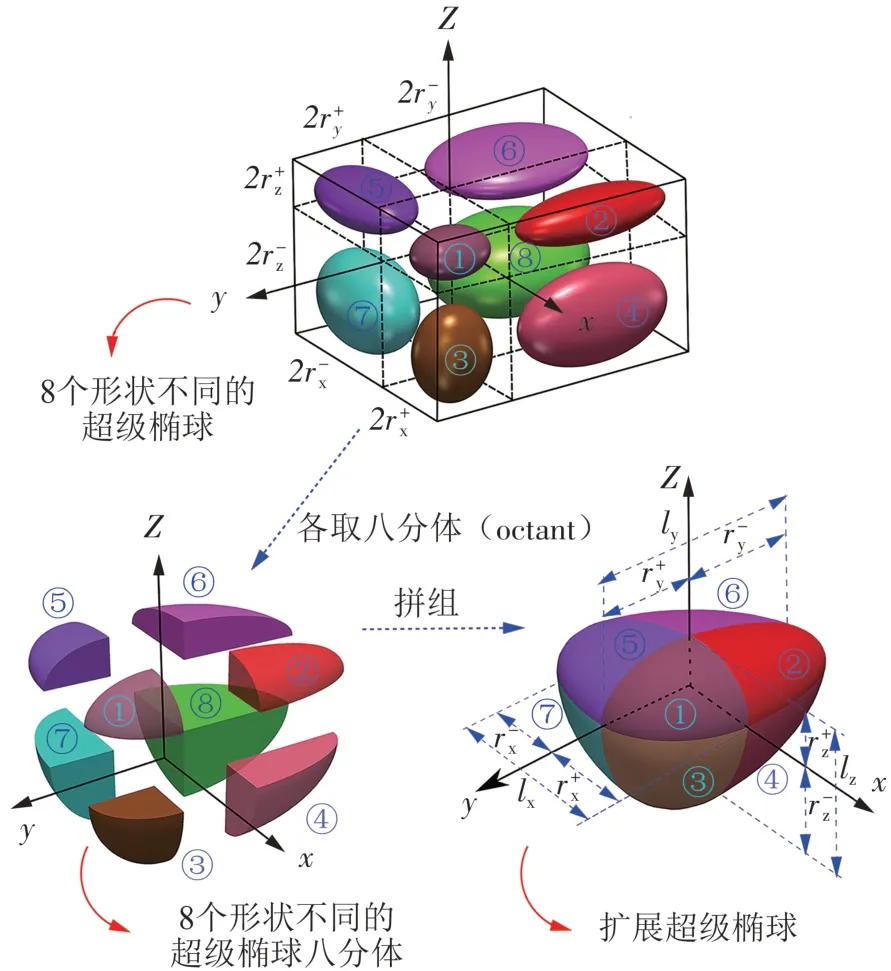
图1 扩展超级椭球的构建原理Fig.1 building principle of poly-superellipsoid

扩展超级椭球表面方程及相关参数为

式中：rix、riy、riz代表第i个八分体在x、y、z主轴的半主轴长；八分体的序号i如图1所示；r+x、r-x分别代表扩展超级椭球在x主轴正负方向上的半主轴长，其他同理；εi1、εi2衡量第i个八分体的表面棱角度。

偏心率具体定义如下

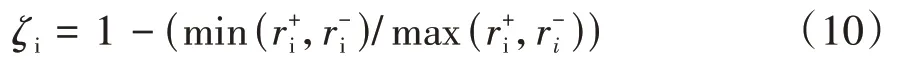
式中：i遍历x、y、z轴；ζi为i轴的偏心率；r+i、r-i分别为i轴在正负方向上的长度。

特别地，本研究独立于颗粒形态棱角度与长细比展开研究，即令ε1=ε2=1.0以及lx=ly=lz。同时将x、y、z轴三个方向的偏心率统一起来，即令ζ=ζx=ζy=ζz并在保证体积一致的情况下将统一后的偏心率ζ设置为0、0.2、0.4、0.6、0.8，以S1-S5分别代之。

数值模拟基于笔者所在团队开发的非球颗粒开源离散元程序SudoDEM［25，46］。颗粒接触模型采用线性弹簧模型及库伦滑移模型。扩展超椭球接触检测及计算的详细信息参见https：//sudodem.github.io。

1.2 数值模拟流程

1.2.1 试样制备

参考Zhou等［47］采用的半径扩大法生成如图2所示的试样，其中颗粒等效直径即等体积球直径。试样尺寸为11.36 mm×11.36 mm×11.36 mm，其与最大颗粒直径之比为13.36，满足Jamiolkowski等［48］为减小尺寸效应和应变局部化而提出的标准。颗粒数目为6000个（预试验证明此颗粒数目已达基本要求）。模拟不考虑重力以避免原生各向异性影响。

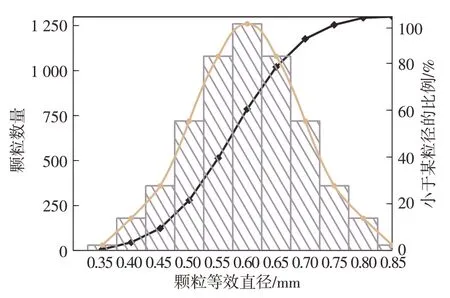
图2 离散元试样生成Fig.2 Generations of DEM specimens

模拟细观参数如表1所示。保证模拟稳定的前提下采取密度放大法将颗粒材料密度放大106倍［18，49］后可将时步提升至5×10-5s。接触刚度采用100MPa×r［18，50］，其中r为颗粒等效半径均值。进行准静态模拟时，系统惯性系数Iinertia不超过0.001［51-52］，即

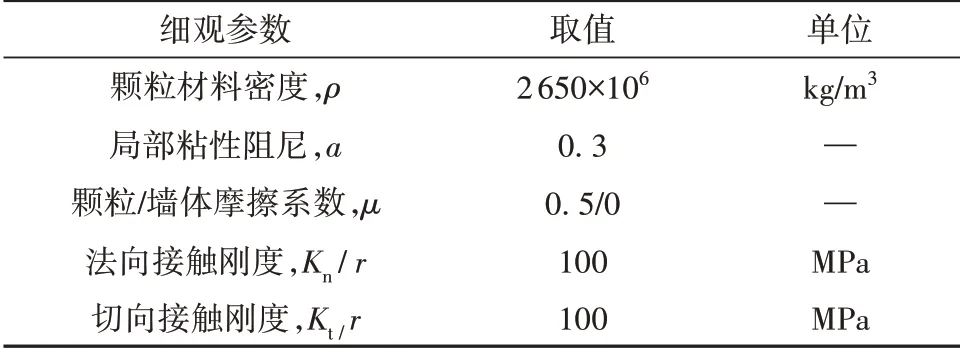
表1 DEM数值模拟细观参数Table 1 Meso-parameters used in the DEM simulations

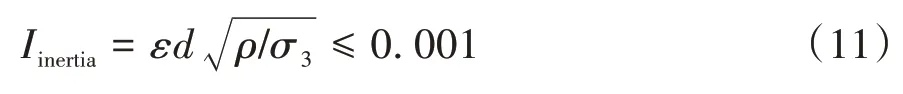
式中：ε为轴向加载应变率，控制为0.01/s；d为颗粒等效直径的均值（0.6 mm）；ρ为颗粒材料密度（2 650×106kg/m3）；σ3为围压（100 kPa）。经计算Iinertia为0.000 976，满足准静态模拟标准要求。

1.2.2 模拟方案

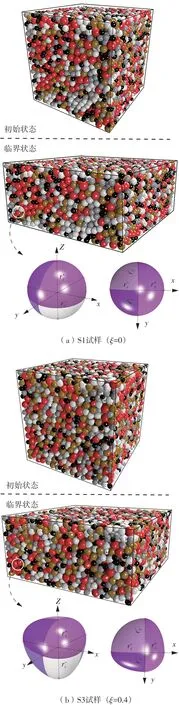
数值模拟分固结与剪切两个阶段，如图3所示。固结过程生成初始各向同性试样，而剪切过程研究次生各向异性的演化。固结开始前，固定边界墙位置不动的同时周期性施加人工阻尼使系统快速稳定，然后按应力控制伺服机制，让颗粒在100kPa围压下固结，此过程调控摩擦系数［18］来保证不同颗粒形状试样的初始孔隙比一致为0.626［24，33，53］。固结完成后开展真三轴剪切，即顶底两面墙以0.01/s的恒定应变加载速率相向移动，侧壁四面墙按应力控制伺服机制独立移动，维持围压100 kPa。为将颗粒间叠合量控制于平均粒径（d50）的0.7%内，最终剪切应变为50%。

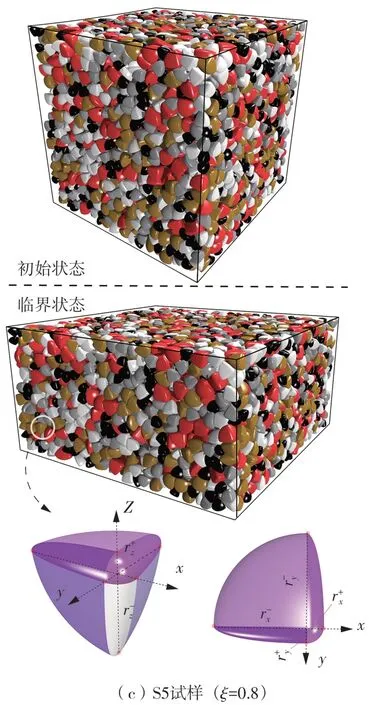
图3 不同偏心率试样的真三轴剪切Fig.3 True triaxial shear of varying eccentricity samples

2 结果分析

2.1 宏观力学响应

参考Christoffersen等［54］基于细观层面颗粒间接触力与支向量来计算应力张量σij。

式中：V为试样体积（包括孔隙体积）；Nc为总接触数；f和l为颗粒间接触力（包含法向与切向）和支向量；i、j∈{ }1，2，3，代表笛卡尔坐标系下x、y、z方向。由于边界光滑，因此试样边界剪应力均为零，即σij为对角矩阵。

平均主应力p和偏应力张量σ′ij采用下式计算：

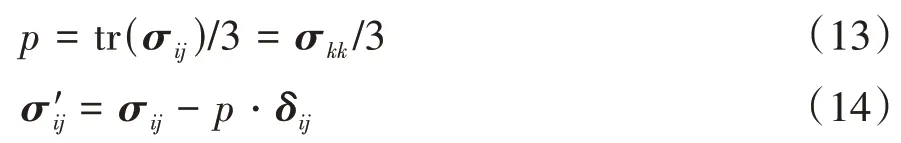
式中，tr(σij)为σij的迹，δij为科罗内多张量。

采用广义剪应力q量化偏应力张量［18］：

式中，σ′ijσ′ij根据爱因斯坦求和约定计算。

由于本研究采用刚性边界墙进行真三轴剪切，可从宏观层面根据边界墙的位移来计算对数轴向应变［18］。

式中，H0、H分别为剪切前和剪切过程的试样高度。

不同偏心率试样的偏应力比q/p随轴向应变的演化曲线如图4所示。可观察到偏心率的小偏差导致了显著不同的宏观抗剪强度演化形态。显然，试样临界强度随着偏心率增大而单调增大，偏心颗粒有着显著增强的临界抗剪强度。这是因为：随偏心率增大，颗粒间法向接触力偏离质心愈明显，产生了更大的绕质心额外力矩［27］，增大了转动阻抗，进而增强了颗粒互锁和咬合牢固性，使得试样可承担更大的剪应力。Kozicki等［55］、Zhao等［36］也有过类似报道。另外，虽试样的初始孔隙比一致，但试样的相对密实度随颗粒偏心率改变而不同。具体地，偏心率较大的试样相对密实度较小，偏心率较小的试样相对密实度较大。因此，随偏心率增大试样逐渐由应变软化转向应变硬化。

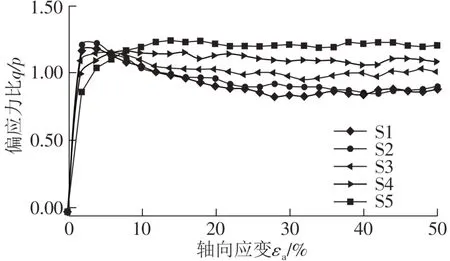
图4 偏应力比-轴向应变曲线Fig.4 Deviatoric stress ratio-axial strain

2.2 细观组构演化

2.2.1 配位数

配位数为表征颗粒材料内部组构的细观标量，某颗粒的配位数即与此颗粒相接触的颗粒数。鉴于配位数为0或者1的颗粒对组构稳定无贡献，本文通过力学平均配位数M描述内部组构稳定性［57］，即

式中：N1表示配位数为1的颗粒数目；N0表示配位数为0的颗粒数目；Nc表示总接触数目（包括颗粒—墙接触）；N表示总的颗粒数目。

力学平均配位数M随轴向应变的演化曲线如图5所示。可见各试样力学平均配位数随应变发展呈指数衰减并最终达临界值，即力学稳定jamming态。根据Rothenburg等［58］和Zhao等［59］的相关研究，配位数的减小主要为密实的试样在剪切过程中体积剪胀所带来的塑性变形所致。另外，随偏心率的增大，配位数下降幅度减小。所以，临界配位数随偏心率单调增加，对应前文所述较高的临界抗剪强度。可能原因为：偏心率愈大，颗粒间接触面积更大，内嵌愈加缜密，因此试样配位数愈大，内部组构愈稳定，为其拥有更高强度作出细观解释。Santamarina等［60］也指出非球颗粒需要更大的配位数来维持稳定。

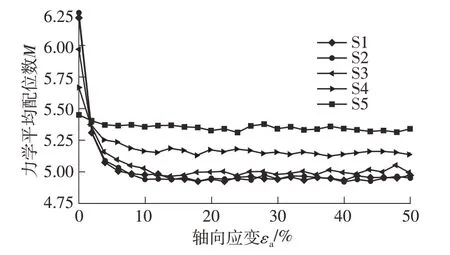
图5 力学平均配位数-轴向应变曲线Fig.5 Mechanical average coordination number-axial strain

2.2.2 接触力传递

接触间承担着或大或小的接触力，当给定接触的法向接触力小于试样的平均法向接触力，此接触即定义为弱接触，反之为强接触。弱接触比例ξw即为弱接触与总接触的数量之比。

颗粒材料在变形过程中往往伴随着颗粒相互滑动。Alonso等［61］认为滑动接触的各向异性为颗粒材料塑性变形的主要原因。滑动接触比例ξs即为滑动接触与总接触的数量之比。

摩擦发挥系数I用于衡量接触间摩擦发挥程度，其定义如式（18）［62］所示。由于切向接触力的计算采用了库伦滑移模型，摩擦发挥系数I不大于1。当I为1时表明接触发生相互滑动，颗粒集合体重新排列。

式中：fn和ft分别为法、切向接触力；μ为摩擦系数。

弱接触比例ξw、滑动接触比例ξs随轴向应变演化以及临界状态（εa=50%）的摩擦发挥系数概率分布（PDF）曲线分别如图6、图7所示。

由图6可见，弱接触比例超过60%并始终大于强接触比例，说明弱接触网格始终比强接触网格承担着更大的作用。Zhao等［33］也曾有过相关报道；弱接触比例及滑动接触比例均随偏心率增大而增大，但后者较前者对偏心率更为敏感。

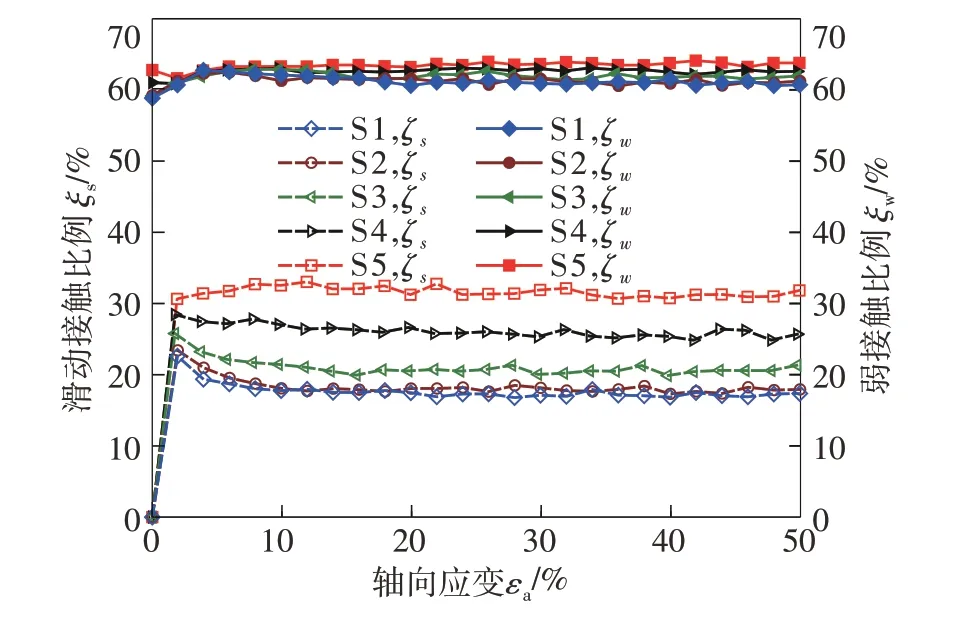
图6 弱接触、滑动接触比例-轴向应变曲线Fig.6 Weak and slide contacts proportion-axial strain

由图7可见，增大的偏心率减小了低摩擦发挥接触的比例并增大了高摩擦发挥接触的比例，当I小于0.75时随偏心率的增大I的PDF逐渐减小，而当I大于0.80时随偏心率增大I的PDF逐渐增大，Nie等［34］也曾得到类似结论。对此，Estrada等［63］曾作相关解释：颗粒的偏心不规则性加剧了接触互锁现象，提高了颗粒抗旋转能力，进而导致颗粒间接触需通过相互滑动来抵抗外荷载。最终，滑动接触比例和高摩擦发挥接触的比例均增大。而从另一角度，根据Zhao等人［24，33］以及Radjai等人［64］的相关研究，绝大部分滑动接触发生在弱接触。换言之，较小法向接触力致最大静摩擦力较易被打破。所以弱接触比例的提升间接导致了滑动接触比例和高摩擦发挥比例的增大。

图7 临界状态摩擦发挥系数PDF分布Fig.7 PDF of friction mobilized index at critical states

通过力链图可将颗粒间法向接触力可视化，进而直观展现各向异性，如图8所示。法向接触力方向由颗粒质心连线（即支向量）代表，而大小则由连线粗细与颜色代表。

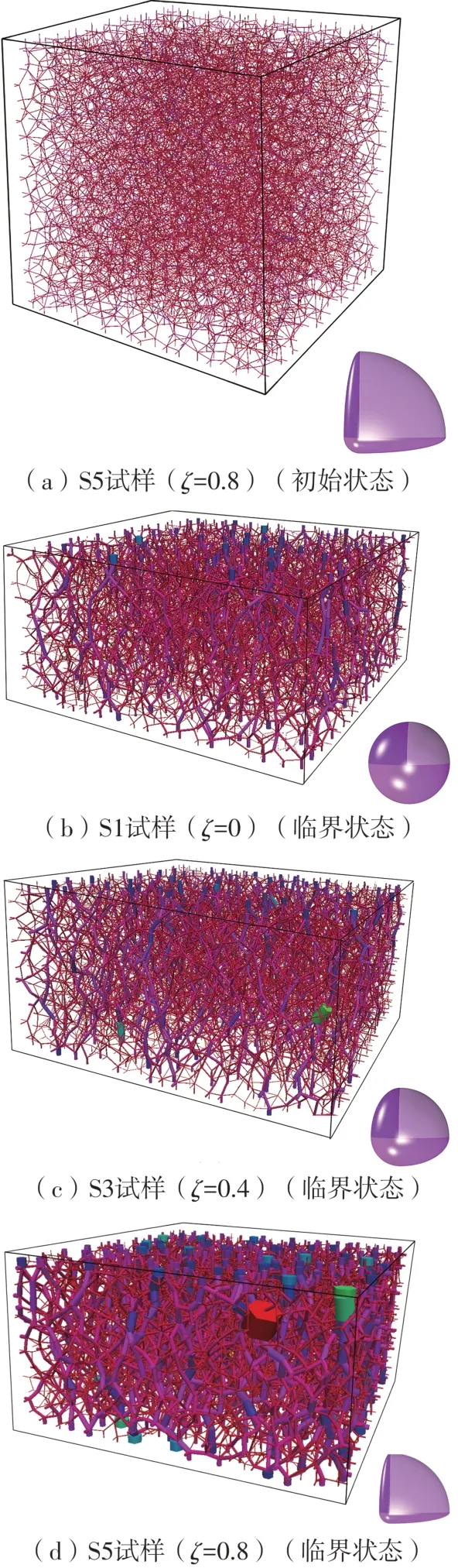
图8 初始及临界状态接触力链图Fig.8 Contact force chains at initial and critical states

各试样在剪切前的力链分布相近，因此仅针对S5试样进行展示，如图8（a）所示。随剪切的进行，稀疏的强力链似柱子般承担着外部竖向荷载并形成有效的传力路径，而密集且始终占据主导地位的弱力链则维持着强力链的稳定。值得注意的是，弱力链几乎呈各向同性分布，而强力链却仅沿竖直加载方向分布，呈现出显著的各向异性，表明强力链主导了法向接触力的组构各向异性，Foroutan等［65］有着类似结论。随偏心率增大，强力链数量上虽无明显变化，但其管径膨胀，加剧了竖直向与水平向法向接触力的各向异性。虽高偏心率试样对应更高的强度（见图4），但其剪应力的承担却更加不均匀。此外如前文所述，随偏心率增大，接触数增大的同时弱接触比例也增大，因此弱力链更密集，保证了强力链的稳定，进而使其可承受更大的外部荷载。

2.2.3 组构各向异性

诸多学者［18，24，28，47，65］通过接触法向、接触力和支向量的组构张量对组构各向异性进行定量描述。

接触法向c指接触的外法线方向，其各向异性可用组构张量φij定量描述［7］，

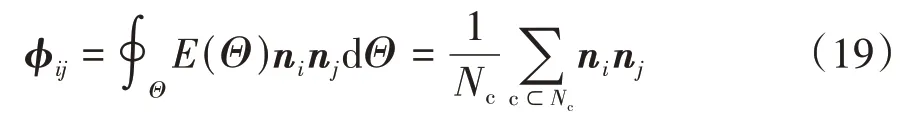
式中：φij为3×3二阶对称张量；Nc为总接触数；n为接触法向单位向量，ni（i∈{1，2，3}）代表n在笛卡尔坐标系下x、y、z3个方向的分量；上式连续空间积分向离散求和形式的转化详见文献［66］。

法向接触力fn、切向接触力ft的组构张量为

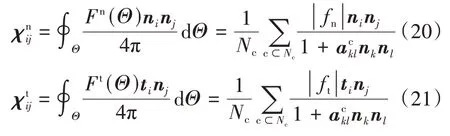
式中：acij为接触法向偏组构张量，详见后文；根据爱因斯坦求和约定计算；|fn|为法向接触力大小；|ft|为切向接触力大小；t为接触切向单位向量，t（ii∈{1，2，3}）代表t在笛卡尔坐标系下x、y、z3个方向的分量。

支向量指颗粒间质心连线。由于颗粒形状的影响，非球颗粒的支向量与接触法向不重合。对此，以接触法向为参考系将支向量分解为法向分量和切向分量，法向支向量dn与切向支向量dt的组构张量分别为

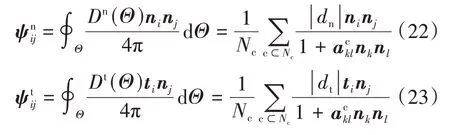
式中：|dn|为支向量在接触法向方向的分量；|dt|为支向量在接触法向的垂直分量。

基于上述认识，5类组构的偏组构张量a*ij分别为

求得偏组构张量后便可通过第二不变量A*来量化各向异性［18］。

式中：a（*ij*代表c、fn、ft、dn、d）t为偏组构张量；σ′ij为偏应力张量；当二者共轴时A*为正，反之为负；5类组构各向异性的第二不变量A*随应变εa的演化曲线如图9所示，随偏心率ζ的演化曲线（在εa为50%的状态下）如图10所示。

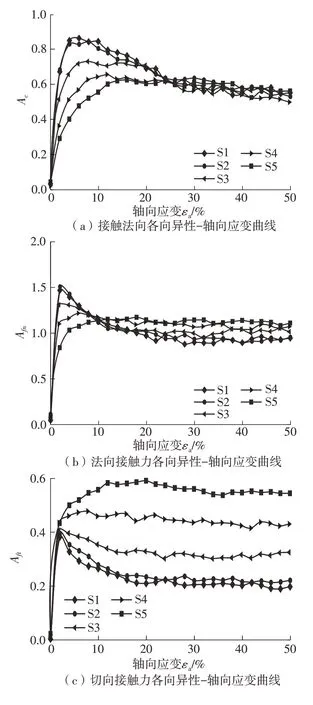
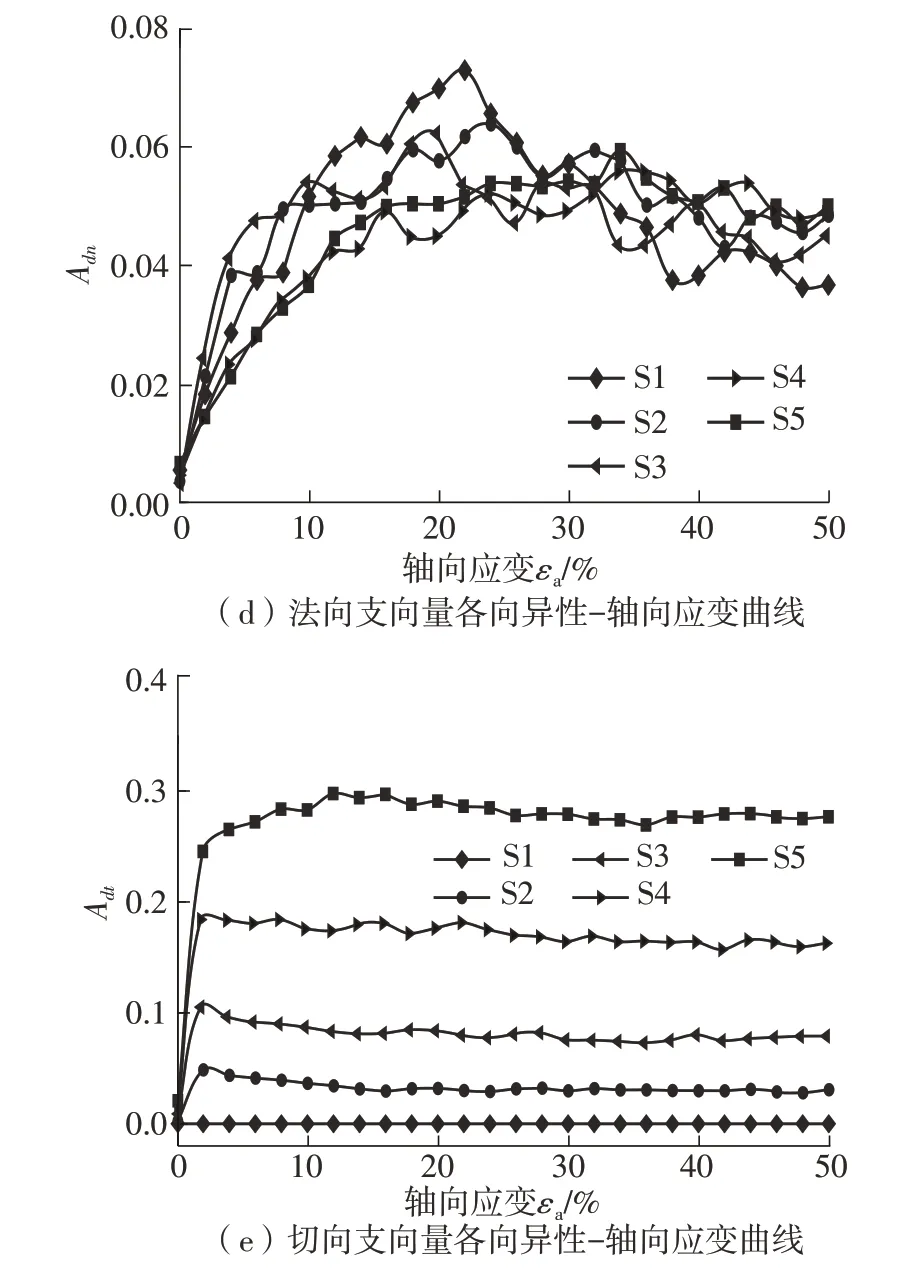
图9 组构各向异性-轴向应变曲线Fig.9 Fabric anisotropy-axial strain

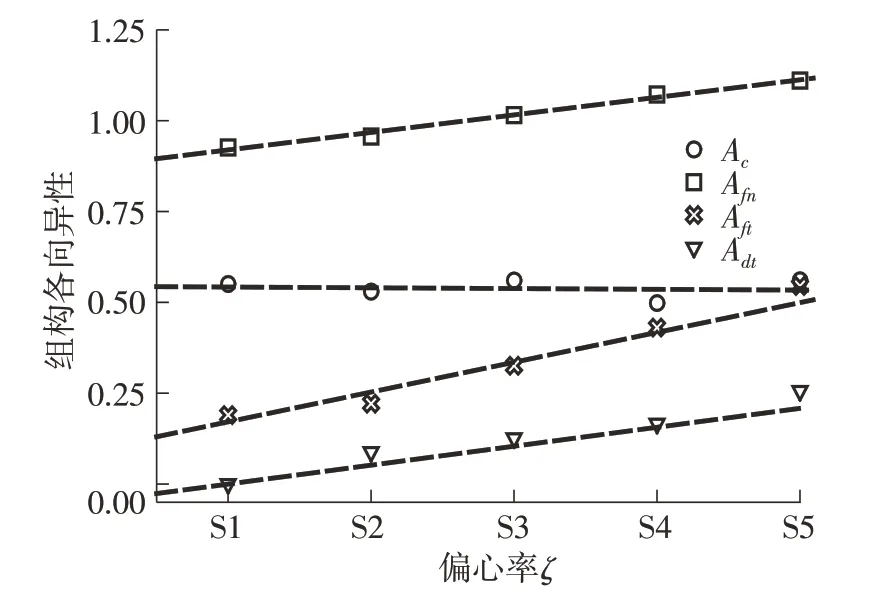
图10 组构各向异性-偏心率曲线Fig.10 Fabric anisotropy-eccentricity

接触法向在单位球面下的概率密度函数E(Θ)为

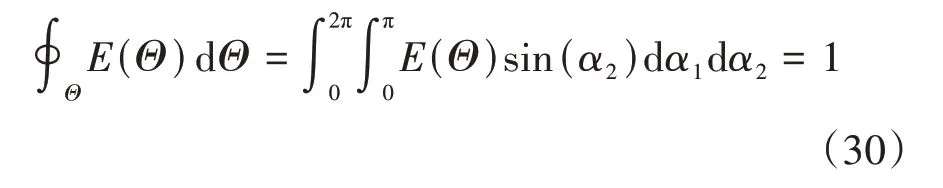
式中：a1∈［0，2π］，a2∈［0，π］。

5类组构在单位球面下的概率密度函数可以用傅里叶级数展开。考虑到方向量的对称性，奇数阶张量对级数解无贡献［67］，可采用二阶傅里叶级数展开［15，65］。

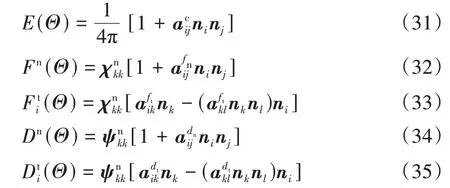
式中：E(Θ)、Fn(Θ)、Fit(Θ)、Dn(Θ)、Dti(Θ)分别为接触法向c、法向接触力fn、切向接触力ft、法向支向量dn、切向支向量dt的概率密度函数。

为将组构各向异性可视化，可基于式（31）-（35）对5类组构的拓扑分布图进行傅里叶拟合。

由于剪切前试样处于各向同性应力状态，5类组构在剪切前也均处于初始各向同性状态。图8（a）中各向同性的弱力链以及图9中5类组构各向异性第二不变量的初始值均为零便作了证明，因此鉴于篇幅有限不对初始状态的组构分布图进行展示。

图9中5类组构各向异性第二不变量A*在剪切过程中的演化各有不同，但均从各向同性状态随剪切发展出次生各向异性，并在不同的应变水平达到不同的各向异性临界状态。其中Ac演化形态最接近图4的强度演化形态。

在试样的临界状态，5类组构的拓扑分布各有不同。从图11可观察到，接触法向c和法向接触力fn的拓扑分布呈“葫芦”状（其中，法向接触力fn的“葫芦”更高且更细）。这是因为，接触法向c和法向接触力fn均在竖直方向（大主应力方向）上一定程度地增长。然而，水平向则不然，甚至出现了收缩现象。这导致了c与fn次生各向异性的产生。另一方面，切向接触力ft与切向支向量dt的拓扑分布呈“双叶草”状。这是因为，ft与dt均在45°+n×90°(n=0，1，2，3)的方向上出现较大幅度的增长。但同时，二者在0°+n×90°(n=0，1，2，3)的方向上却基本保持为零。特别地，ft与dt“双叶草”状的拓扑分布与现实中砂土试样常见的剪切带形态较为相像。这表明，切向接触力ft与切向支向量dt的各向异性与砂土的剪切带有着密不可分的联系。值得注意的是，法向支向量dn的拓扑分布为圆形。这表明，法向支向量dn为各向同性分布或其各向异性可忽略不计。这也是图9（d）中Adn在整个剪切过程中始终很小且其演化曲线崎岖不平的原因所在。

在试样的临界状态，偏心率对组构各向异性的影响也各不相同。偏心率对接触法向c的各向异性影响很小。图9（a）、图11（a）和Zhao等［33］均证明了此结论。另一方面，在图9（b）当中，Afn随偏心率的增大而小幅度地增大；在图11（b）当中，随偏心率的增大，法向接触力的拓扑分布变得更加“高瘦”；在图8中，随偏心率增大，强力链的管径出现了膨胀。这三个现象均表明，偏心率增大了法向接触力fn的各向异性。切向接触力ft的各向异性随偏心率增大而大幅度增长。此观点可从图9（c）中随偏心率增大而大幅增大的Aft、图11（c）中随偏心率增大而整体变大的“双叶草”得出。最后，图9（e）和图11（e）均可表明切向支向量dt各向异性则随偏心率增大而不等幅度增大。这是因为，由接触法向与支向量的不相重合产生的切向支向量随颗粒形态特征偏离球体而逐渐增大［26］。

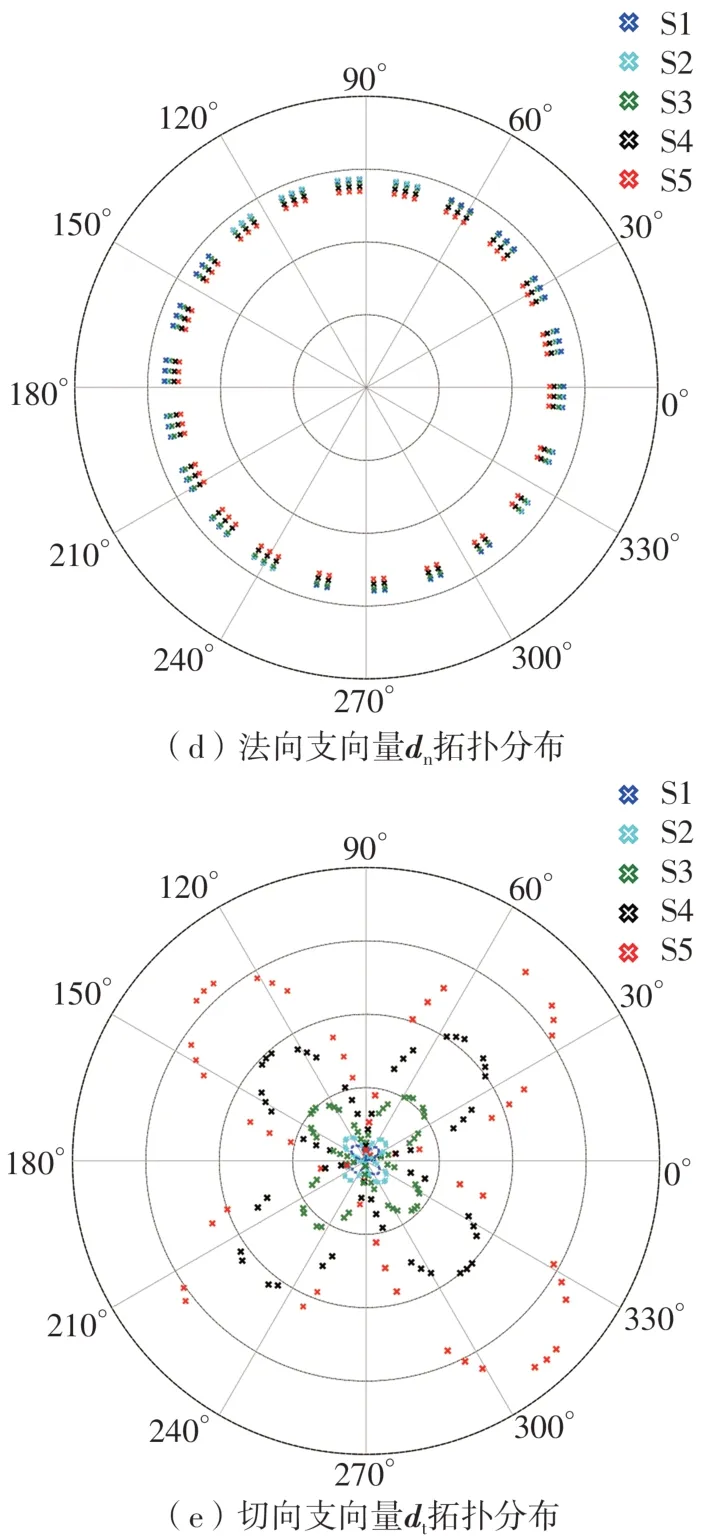
图11 临界状态组构分布图Fig.11 Distribution of fabric at critical state

从图10可见，切向接触力ft、切向支向量dt的各向异性与偏心率的关系线的斜率较高，表明偏心率对二者的影响较大。可以认为，在偏心颗粒试样中，切向接触力ft、切向支向量dt对几何各向异性奉献较大，不应忽视，这与其他学者的结论有所偏差［33］。

5类组构各向异性对剪应力比（宏观抗剪强度）的贡献各不相同。图12展示了5类组构各向异性的贡献比重随轴向应变的演化。从中可见，Afn权重始终最大。这表明，法向接触力fn的各向异性对抗剪强度的贡献最大。同时，在图9（b）中，Afn的演化形态与宏观强度的演化形态始终最为接近，此现象也对上述观点作出了佐证。文献［18，24，31］也曾报道过类似的观点。法向接触力fn及接触法向c各向异性总占比约80%，而其余三者权重均较小。这表明接触法向c与法向接触力fn各向异性对强度的贡献较大。

图12 组构各向异性比重-轴向应变曲线Fig.12 Weights of fabric anisotropy-axial strain

随轴向应变的发展，Ac的贡献比重呈现出先增加后减小的趋势，Afn的贡献比重则呈现出先减小后增大的趋势。它们分别在约15%的轴向应变处达到峰值与谷值。这说明，剪切过程中Ac的权重和Afn相互转移。这意味着，剪切过程中几何各向异性与力学各向异性相互转化。其原因正如Zhao等［33］所述：剪切过程中因剪胀而不断减小的平均配位数使得接触分散性降低。

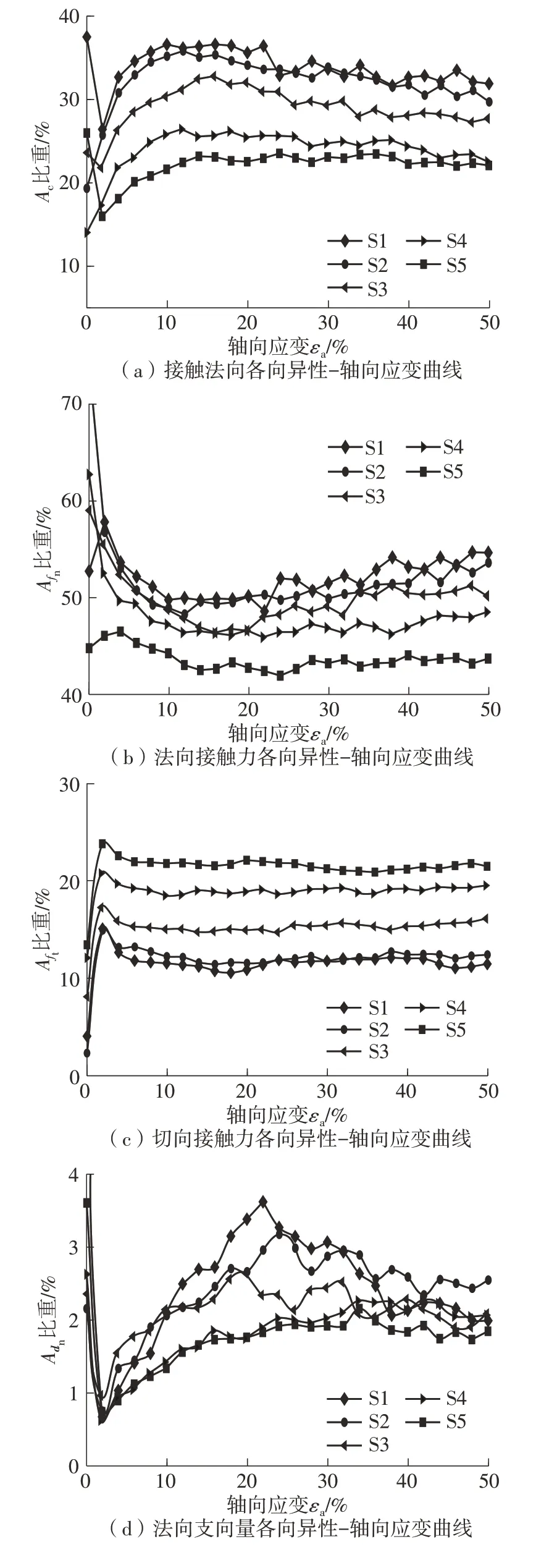
在偏心率的影响方面，从图12得知，随偏心率增大，Ac、Afn的相对权重减小，Aft的相对权重增大。这表明，偏心率的增大会让法向接触力的各向异性向切向接触力的各向异性转化。此观点解释如下：一方面，如前文所述，弱力链呈各向同性，强力链才为法向接触力各向异性的主导。Guo等［18］也曾指出，强接触网格中法向接触力各向异性比弱接触网格大得多。因此，随偏心率增大，弱力链比例的提高、强力链比例的减小导致了法向接触力各向异性比重的减小；另一方面，Sufian等［68］认为：滑动接触网格中切向接触力的各向异性相比法向接触力各向异性更大。也即，较高偏心率带来的滑动接触比例的增大会导致切向接触力各向异性比重增大。综合两方面原因，偏心率的增大会让法向接触力各向异性向切向接触力各向异性转化。

3 结论

基于笔者所在团队开发的非球颗粒开源离散元程序SudoDEM，开展了扩展超级椭球的颗粒趋真建模，进行了不同偏心率试样的真三轴剪切。基于组构张量表征各向异性，并通过二阶傅里叶拓扑拟合图和力链图将各向异性可视化，着重分析了颗粒偏心率对颗粒介质细观次生各向异性演化的影响，得到以下主要结论：

（1）随偏心率增大，细观组构各向异性不同程度地发展，共同承担着宏观抗剪强度的提升。同时，临界配位数更大，滑动接触比例更高，接触力网格的空间非均匀性也愈加显著。这主要因为颗粒偏心增强了颗粒间的互锁与咬合。

（2）三轴剪切发展了次生各向异性。五种组构各向异性表现各不相同，并在不同的应变水平达到各向异性临界状态。其中，法向接触力与接触法向的空间分布呈“葫芦”状，前者的各向异性演化形态最接近强度演化形态，并始终占据最大权重；后者的各向异性权重次之（二者总占比约80%）；法向支向量空间分布为圆形，其各向异性可忽略不计；切向接触力及切向支向量的空间分布呈颇似剪切带的“双叶草”状。特别地，二者受偏心率影响较为敏感，在偏心颗粒试样中二者对强度的贡献不可忽略。

（3）剪切过程中几何各向异性和力学各向异性相互转化；随偏心率增大，法向接触力各向异性逐渐向切向接触力各向异性转化。