改进的指数函数方法求时空分数阶混合(1+1)维KdV方程的新精确解

陈兆蕙，阳平华*

(广州城市理工学院计算机工程学院，广东 广州 510800)

受“孤立波”现象的启发，荷兰数学家Korteweg和deVries在研究关于浅水问题中的小振幅长波运动时合作发现了KdV方程。这是一种典型的非线性色散波动方程，物理学中的很多现象如：固态物理、冷等离子的磁流波、声波的传播、量子场、离子-声子波、非谐振晶格振动等都可以用这种方程来解释[1]。研究这类方程的精确解能给物理学提供可靠依据，也能加强数学和其他学科之间的紧密联系，所以研究它的精确解很重要。由于对分数阶偏微分的研究比整数解偏微分方程应用范围更为广泛、也更能准确表述物理和其他学科的特性，因此目前有(G'/G)-展开法和一般的tanh方法[2-6]、首次积分法[7-8]、改进的Riccati方法[9]、拟设法[10]、改进的Kudryashov方法[11-12]、Hirota方法[13-14]等研究分数阶偏微分方程，并且得到了多种不同类型的解。

本文在其他作者研究工作[1-17]的基础上，探讨一类时空分数阶混合(1+1)维KdV方程

(1)

其中a0,a1,a2是非线性系数，β是色散系数，这些系数都不为零且α满0<α≤1.当a0=a2=0，方程(1)变成了时空分数阶KdV方程[15]，张志惠[15]使用指数展开法求解出了该方程的精确解；当a0=0，方程(1)变成了时空分数阶KdV-mKdV方程[16]，赖晓霞[16]采用改进后的指数展开法研究了该方程的精确解，并采用符号计算软件给出了解的三维立体图形。本论文同文献[15-16]相比，方程项数增加，难度增大；同文献[17]相比，虽然研究的是同一个方程，但是文献[17]采用的是首次积分法，本文采用改进的指数函数方法[15-16]。研究方法不同，本论文拓展了方程(1)的新精确解，且新精确解更加丰富。

Jumarie的修正Riemann-Liouville分数阶导数[15-16]按照如下定义：

定义1

定理1[15]

Jumarie的修正Riemann-Liouville分数阶导数具有以下性质：

1 时空-分数阶混合(1+1)维KDV方程

首先对方程(1)作分数阶变换，令

(2)

这里的w是待定常数。将(2)式代入(1)式，有-wu′+a0u′+a1uu′+a2u2u′+βu‴=0，对上式积分一次，并且令积分常数为零，得到

(3)

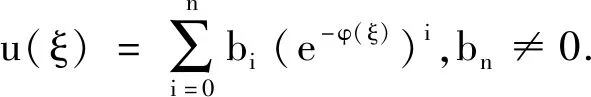
综合考虑式(3)中u″和u3最高阶次数须达到平衡，即3n=n+2，得出n=1，从而

(4)

且φ(ξ)满足下列常微分方程

φ′(ξ)=pe-φ(ξ)+μeφ(ξ)+λ

(5)

其中p,μ,λ为待定常数。

将式(4)和式(5)代入式(3)，有

合并(e-φ)i(i=0,1,2,3)的相同幂次项，有

令(e-φ)i(i=0,1,2,3)的各个系数等于零，得到一个关于b0,b1,w的代数方程组：

由上述方程组，得到b0,b1和w满足如下方程

由于约束条件不一样，得到的解也不相同。下面分情况讨论方程的新精确解。

2 时空-分数阶混合(1+1)维KdV方程的新精确解

第一种情形：

p=1,λ2-4μ>0,λ≠0,μ≠0,得到参数值如下：

此时

φ1(ξ)=

有新精确解

(6)

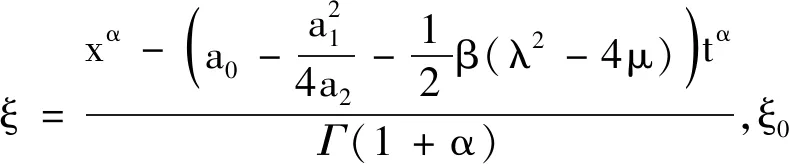
第二种情形：

p=1,λ2-4μ<0,λ≠0,μ≠0,得到

参数值如下：

此时

φ2(ξ)=

得新精确解

(7)

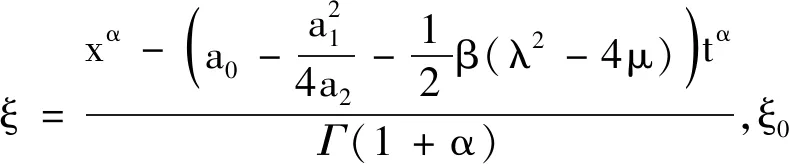
第三种情形：

p=1,λ2-4μ>0,λ≠0,μ=0,得到参数值如下：

(8)

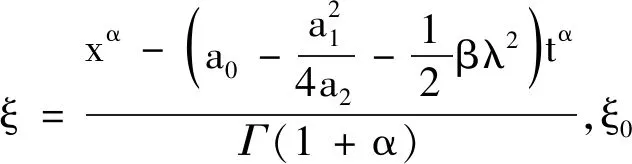
第四种情形：

p=1,λ2-4μ=0,μ≠0,λ≠0，得到参数值如下：

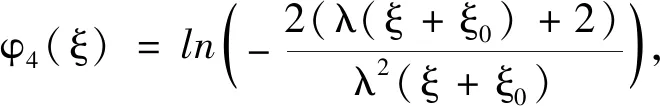
(9)

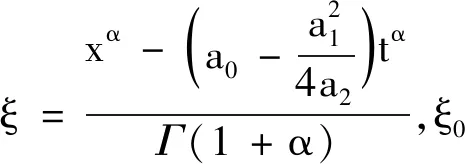
第五种情形：

λ=0,p>0,μ>0,得到参数值如下：

此时

或

得新精确解

(10-1)

或

u5-2(ξ)=b0+b1e-φ5-2(ξ)

(10-2)

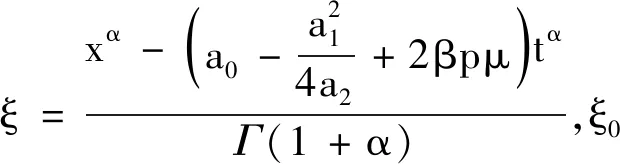
第六种情形：

λ=0,p>0,μ<0,得到参数值如下：

此时

φ6-1(ξ)=

或

φ6-2(ξ)=

得新精确解

或

(11-2)

第七种情形：

λ=0,p<0,μ>0,得到参数值如下：

此时

φ7-1(ξ)=

或

φ7-2(ξ)=

得新精确解

(12-1)

或

(12-2)

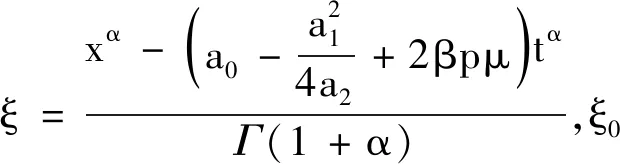
第八种情形：

p=1,μ=0,λ=0,λ2-4μ=0，得到参数值如下：

此时

φ8(ξ)=ln(ξ+ξ0)

得新精确解

(13)

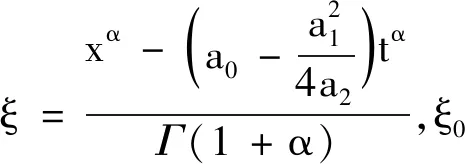
3 图形绘制

为了更直观表示图形，这里对具有代表性的第一种情形下的精确解进行计算机仿真.取

限制0≤t≤6,0≤x≤8,得到图形如下：

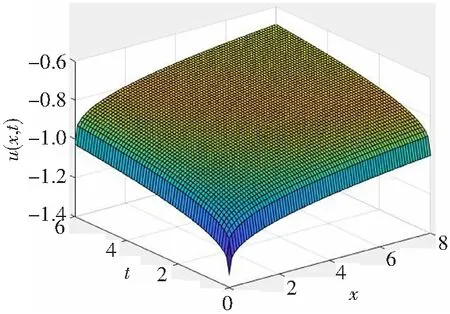
图1 α=0.3时第一种情形下的精确解图形Figure 1 The exact solution of the graph in the first case with α=0.3

图2 α=0.9时第一种情形下的精确解图形Figure 2 The exact solution of the graph in the first case with α=0.9

4 结论

本文使用改进的指数函数展开法扩充了时空分数阶混合(1+1)维KdV方程的新精确解。说明改进的指数函数方法对于求解分数阶方程有实用性和优越性。但是文中这类时间分数阶方程可否使用其他方法如：不变子空间方法、动力系统分支法等方法来研究它的新的精确解呢？这是后续研究的方向。