广义连续框架的参数型不等式
2022-02-04相中启陈裕先
相中启,陈裕先
(新余学院数学与计算机学院,江西 新余 338004 )
1952年,Duffin和Schaeffer[1]在深入研究非调和Fourier级数时引入(经典)框架的概念,他们借鉴了Gabor关于信号处理的基本思想。1986年,Daubechies等[2]重新引入并进一步发展了框架理论,他们的突破性研究开启了小波飞速发展的新时代。自此,框架作为一个重要工具已被工程师和应用数学家广泛应用于信号处理、图像处理和抽样理论等方面[3-6]。
受量子光学理论中的一个重要分支—相干态理论的启发,Kaiser[7]、Ali等[8]分别独立地利用测度空间将框架概念进行推广,由此产生了连续框架的概念。目前连续框架已被广泛用于短时Fourier变换和连续小波变换等方面[9-12]。
基于算子理论的观点,孙文昌教授将框架进行离散推广,提出了广义框架(或简称为g-框架)的概念,他将Hilbert空间中的几种已知框架的推广形式做统一讨论,得到了一些重要成果[13-14]。广义连续框架(或简称为g-连续框架)的概念由Dehghan和HasankhaniFard[15]引入,它是广义框架和连续框架的自然拓广。
在研究信号重构的有效算法时,Balan等[16]建立了Parseval框架的新等式,在进一步讨论此等式时他们发现了Parseval框架的一个有趣的不等式,随后Gavruta[17]将其推广到一般框架的情形。最近,Xiao等[18]证明了前述Parseval框架和一般框架的不等式对广义连续框架依然成立。本文利用算子理论方法构建了广义连续框架的包含参数λ∈[0,1]的新型不等式,该结果包含了文[18]中的相应结果,另外得到了广义连续框架的在结构上不同于已有不等式的参数型双向不等式。
1 准备工作
为了方便起见,先约定一些记号。本文中H和K是复的Hilbert空间,(Ω,μ)是赋有正测度μ的测度空间,{Kω}ω∈Ω是K的闭子空间族。任意ω∈Ω,用记号L(H,Kω)表示由H到Kω的有界算子的全体。记号L表示复数集,IdH表示H上的恒等算子。
定义1[15]算子族Γ={Λω∈L(H,Kω)}ω∈Ω称为H关于(Ω,μ)的广义连续框架,如果下面两个条件满足:
(1)Γ是弱可测的,即任意f∈H,ω→Λω(f)是Ω上的可测函数;
(2) 存在常数0 如果C=D=1,则称{Λω}ω∈Ω是H关于(Ω,μ)的Parseval广义连续框架。 注1如果Ω是可数集,μ是计数测度,则广义连续框架即为文[13]中的广义框架。任意Λ∈L(H,),由Riesz表示定理知存在g∈H使得任意f∈H,Λ(f)=〈f,g〉。所以,如果任意ω∈Ω,取Kω=,则广义连续框架等价于连续框架。 设{Λω∈L(H,Kω)}ω∈Ω是H关于(Ω,μ)的广义连续框架,其框架算子定义为: (1) (2) (3) (4) 所以 〈S-1SΩ1f,Sf〉+〈S-1SΩ1f,SΩ1f〉+〈SΩ1f,f〉=〈S-1SΩ1f,SΩ1f〉+〈f,Sf〉-〈f,SΩ1f〉= (5) 注意到 所以由(5)式可得 设{Λω∈L(H,Kω)}ω∈Ω是H关于(Ω,μ)的Parseval广义连续框架,则其框架算子S=IdH。于是任意Ω1⊂Ω,f∈H有 (6) 类似地有 (7) 于是由定理1立即可得: 推论1设{Λω∈L(H,Kω)}ω∈Ω是H关于(Ω,μ)的Parseval广义连续框架,则对任意的Ω1⊂Ω,λ∈[0,1]以及f∈H有 下面给出在结构上不同于文[18]中和定理2.1中的不等式的广义连续框架的新型参数不等式。 (8) 和 (9) 由此可知SΩ1-SΩ1S-1SΩ1≥0。于是任意f∈H可知 0≤〈SΩ1f,f〉-〈SΩ1S-1SΩ1f,f〉=〈SΩ1f,f〉-〈S-1SΩ1f,SΩ1f〉= (10) 另一方面,任意f∈H,由(4)式可得 (11) 联合(10)和(11)就证明了不等式(8)。下面证明不等式(9)。任意f∈H,由(5)式得 (12) (13) 联合(12)和(13)即得(9)。 由(6),(7)和定理2立即可得: 推论2设{Λω∈L(H,Kω)}ω∈Ω是H关于(Ω,μ)的Parseval广义连续框架,则对任意的Ω1⊂Ω,λ∈[0,1]以及f∈H有 和 本文从算子理论的视角建立了广义连续框架的与参数λ∈[0,1]相关的新的不等式,事实表明,当选择合适的λ时,已有的一些结果可以作为其特例而得到。此外,借助参数λ∈[0,1]构建了广义连续框架的双向不等式,其在结构上不同于已有的不等式。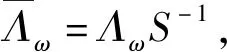
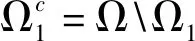
2 主要结果及其证明
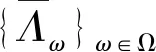

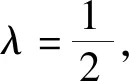
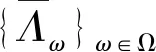


3 结语
