一般树型线条件下的列车开行方案优化研究

魏润斌 贾顺平，2† 童瑞咏 张书婧

（1.北京交通大学交通运输学院，北京 100044；2.北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

国内外各大城市的轨道交通系统均已成网运行，随着复杂方向上客流出行带来的交通供给与需求不匹配问题的日益严重，网络化运营组织技术应运而生并取得了良好的效果，共线运营、直通运营、多交路运营成为了常见的方法［1］。与单线运营不同，网络化运营组织技术需要线路之间的互联互通作为基础条件，从而推动了复杂线路形态的出现，如Y型线［2］、X型线［3］。

Y型线是指由一个干线和一个支线组成的轨道交通线路，干线服务于高客流密度地区，支线服务于低客流密度地区［4］。国内外学者对Y型线条件下的列车开行方案展开了大量研究，Riejos等［5］优化了径向骨干网络中的干线和支线设计，Fioole等［6］研究了铁路机车的车辆周转问题。近年来，国内学者也针对Y型线开行方案进行了大量研究，如表1所示。由表1可见，现有研究大多以交路方案、发车频率为决策变量，以乘客出行时间和企业运营成本最小为目标，采用站站停的停站模式和固定编组的编组方案。

表1 近年来国内学者针对Y型线开行方案的研究Table 1 Researches on train planning for Y-type rail transit by Chinese scholars in recent years

本研究借鉴既有的Y型线的研究成果，提出了一种全新的线路形式——树型线。树型线是Y型线的进阶形式，同样只拥有一条主干线路，但是拥有更多的分支形成了树的形态，从而具有更复杂的客流空间特征和更多的交路组织形式。投入实际运营的树型线的线路是真实存在的，如巴黎的RER A和RER B、东京私铁线路组合等均为一般树型线的表现形式，如图1所示。

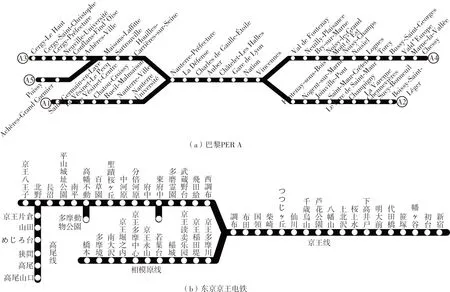
图1 一般树型线线路图Fig.1 Route maps of general Tree-type line

从图1（a）和1（b）中可以发现，树型线的线路往往在城市（远）郊区通过低频次的支线运营提高线路覆盖率，在城市近郊和核心区通过高频次的干线运营提供大通道的通勤服务。树型线可分为直径型和半径型，直径型的如RER A线，干线贯穿城市中心，干线两端均布置多条支线；半径型的如京王电铁线，干线一端深入城市中心，另一端布置多条支线。

现有关于网络化运营组织技术的研究主要针对多交路运行和共线运营，线路形态一般比较简单，而针对树型线这种复杂线网结构条件下的列车开行方案的研究尚不多见。因此，本研究根据树型线定义，设计了一般树型线的线路拓扑形态，以发车频率和运行交路为决策变量，以乘客出行时间与企业运营成本最小为目标函数，构建了一般树型线条件的列车开行方案优化模型，并设计了NSGA-Ⅱ算法求解了开行方案的帕累托前沿解。最后，以RER A线为例对模型和算法的合理性和高效性进行了验证。

1 问题描述

为便于问题描述，并且不失一般性，文中构建了一般树型线的线路示意图，如图2所示。

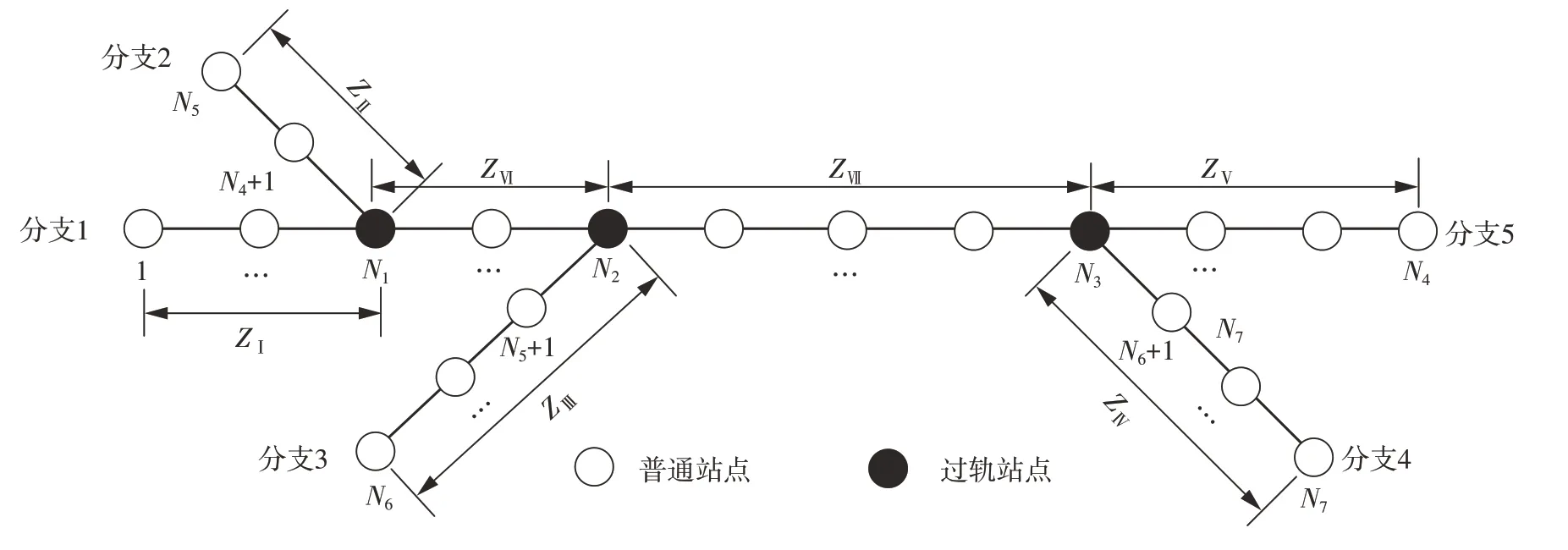
图2 一般树型线示意图Fig.2 Schematic diagram of general Tree-type line

图中，车站1至车站N4为干线，为便于模型建立，干线两端分别设为分支1和5；分支2、3、4为支线，N1、N2、N3分别为各支线的过轨站。根据线路拓扑结构，全线可分为多个区段，由ZⅠ、ZⅡ等表示。由于多交路共线运行情况下增加小交路折返会造成线路通过能力的损失，为了简化处理，本研究假设所有的列车都需要往返于干线或支线的尽端，并都通过核心城区。

2 模型建立

2.1 模型假设

一般树型线条件下的轨道交通开行方案的编制受多种因素影响，根据建模及算法求解形式要求，结合既有研究做出以下假设：

（1）所有列车均采用站站停模式，不存在跨站及越行情况；

（2）研究时段内乘客到达强度均匀，不存在留乘情况且平均候车时间为发车间隔的一半；

（3）乘客选择搭乘到达车站后的第一辆车，因此客流在各列车中的分配比例，由不同类型列车的发车频率等特征决定；

（4）不考虑不同线路列车在过轨车站的互相干扰。

2.2 参数及变量定义

文中模型所用参数、中间变量及决策变量见表2。

表2 参数及变量Table 2 Parameters and variables

为便于理解，文中对部分中间变量进行说明和数学定义。

（1）断面客流pupn

文中设定分支1至分支5方向为上行方向，通过OD客流可以求得各区间断面客流，以属于区段ZⅥ的区间为例，断面客流可由下式求得：

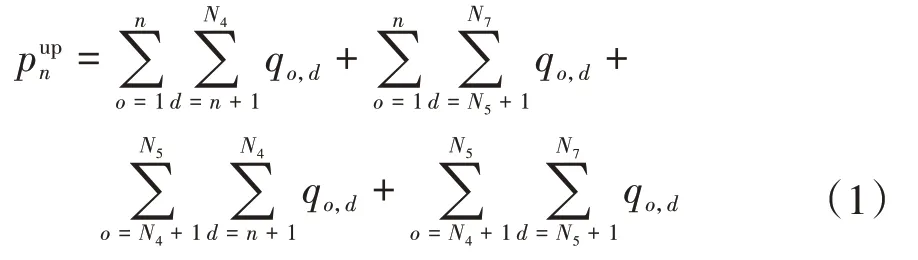
式中，n∈[N1，N2-1]。

同理可以求得其他区间的上下行断面客流。

（2）交路长度Li，j

文中构建的一般树型线条件下的交路备选集共有6种，以分支3和分支5的交路为例，交路长度可由下式求得：

同理可以求得其他交路的长度。

（3）满载率ηupn

根据断面客流与该区间内运行的列车可以求得各区间满载率，以上行方向属于区段ZⅥ的区间为例，满载率可由下式求得：

式中，n∈[N1，N2-1]。

同理可以求得其他区间的上下行满载率。

2.3 目标函数

列车开行方案的编制需要同时考虑乘客出行时间与企业运营成本。

2.3.1 最小化乘客出行时间

由于不同的交路组织形式几乎不改变乘客的在车时间，所以文中的乘客总出行时间只包括乘客总候车时间与总换乘时间。由于树型线条件下具有多种交路形式，导致部分交路列车的发车频率很低，如果所有乘客只选择直达列车的话会导致候车时间大量增加。因此，本研究假设乘客会选择候车时到达的第一辆列车乘坐，这导致了可供乘客选择的列车组合是极其复杂的，以ZⅠ区段出发的乘客为例进行分析。由ZⅠ区段出发，前往ZⅠ、ZⅥ、ZⅦ的乘客只能选择由分支1出发的列车；前往ZⅡ、ZⅢ的乘客必须选择由分支1出发的列车后再换乘到达分支2或者分支3的列车；前往ZⅣ、ZⅤ的乘客既可以选择直达列车，也可以选择搭乘由分支1出发前往其他分支的列车后再换乘前往该区间所在分支的任一列车。综上，乘客选择列车的决定因素是不同交路列车的发车频率，发车频率更高的列车会被更多的乘客选择。基于此，可以计算乘客总换乘时间和候车时间，限于篇幅，同样以ZⅠ区段出发的乘客为例，候车时间可由下式得到：

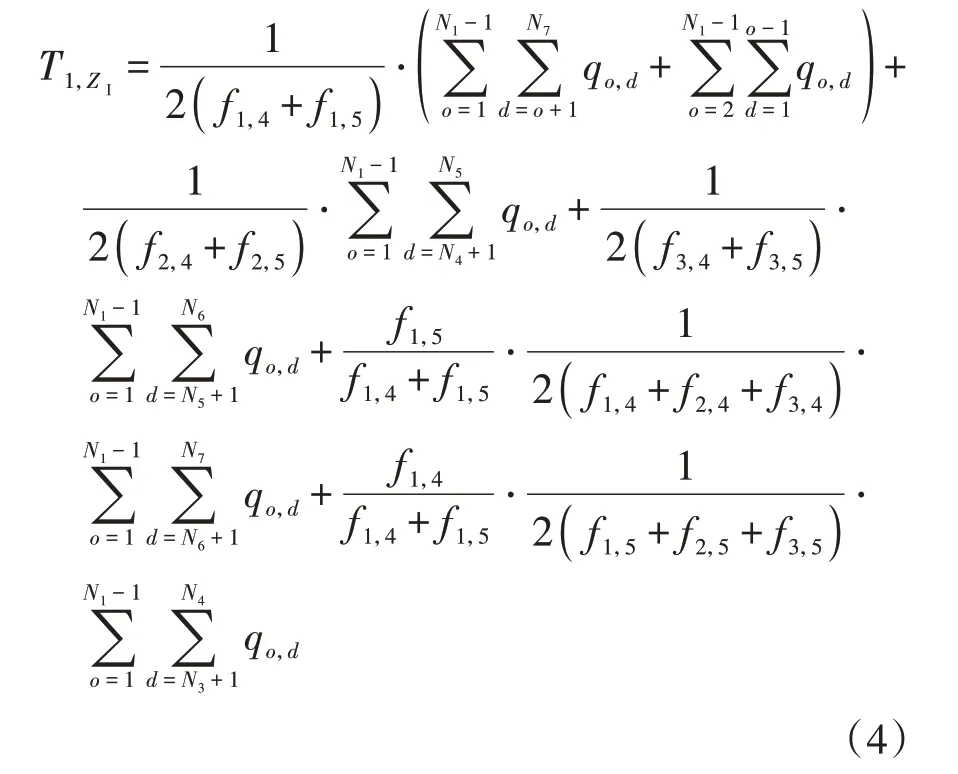
以ZⅠ区段出发的乘客为例，换乘时间可由下式得到：

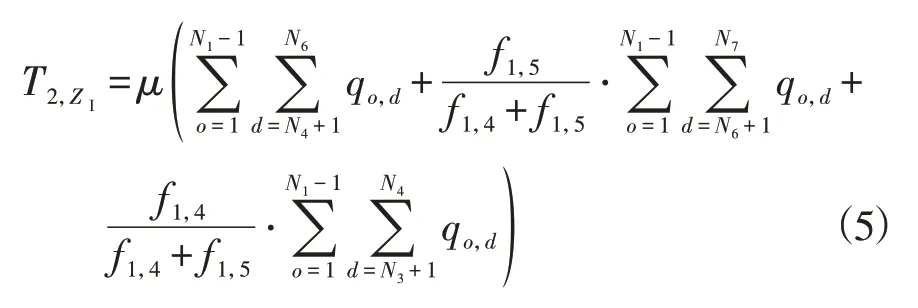
同理可以求得所有乘客的候车时间和换乘时间，最小化乘客出行时间为

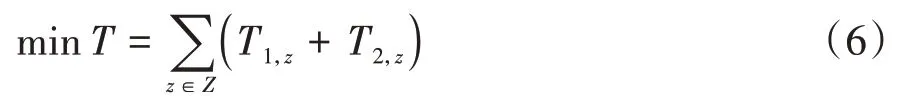
2.3.2 最小化企业运营成本

企业运营成本包含范围较广，针对文中的一般树型线条件下的列车开行方案编制问题，选用车辆运营成本和车辆使用成本作为代表。车辆运营成本由列车总走行里程和每公里的运营成本表示，最小化车辆运营成本为

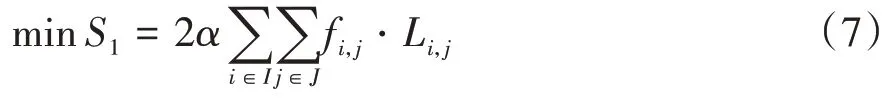
车辆使用成本，指车辆使用过程中产生的损耗费、折旧费等。参考文献［12］中的计算方法，考虑到车辆备用的需要，所需列车数量取运用车数的1.2倍，最小化车辆使用成本为

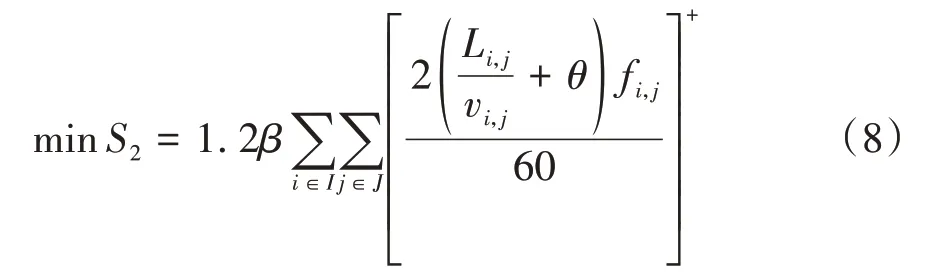
因此，最小化企业运营成本为

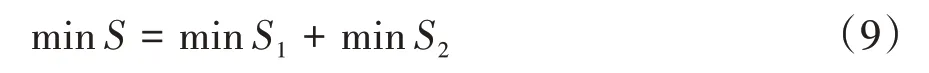
2.4 约束条件

模型中部分变量需要满足相应的约束条件，如式（10）-（14）所示。

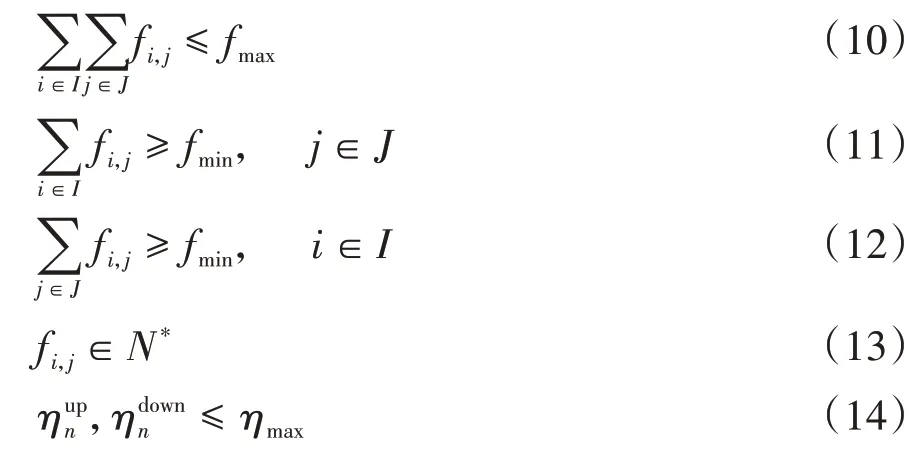
式（10）表示共线运营区段内的发车频率需要满足列车最大发车频率的约束，列车最大发车频率由线路条件限制；式（11）和式（12）表示各支线内的列车发车频率需要满足列车最小发车频率的约束，列车最小发车频率由最低乘客服务水平限制；式（13）保证发车频率为正整数；式（14）为列车满载率约束。

3 算法求解

前文所建模型为非线性整数规划模型，且目标函数和约束条件中均存在非线性项，难以进行线性化处理和精确求解。其次，模型中包含乘客出行时间和企业运营成本两个目标，属于多目标优化问题。因此，本研究设计了NSGA-Ⅱ求解开行方案的帕累托前沿解，供决策者参考。

文中求解流程如图3所示，具体步骤如下。

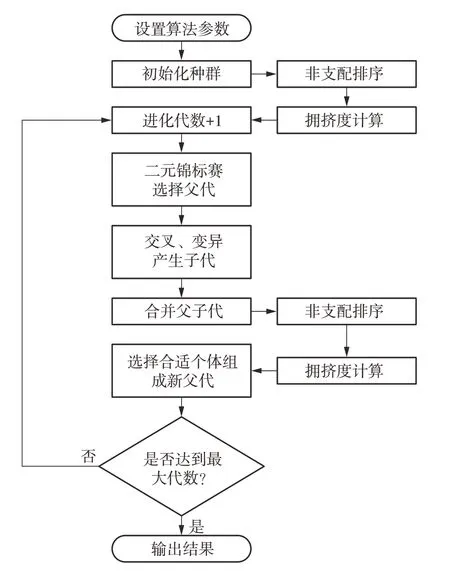
图3 NSGA-Ⅱ算法流程Fig.3 Process of NSGA-II algorithm

步骤1设置算法参数。种群规模Ps、进化代数G、交叉概率Pc、变异概率Pm。

步骤2初始化种群。随机生成符合约束的可行解，重复该过程Ps次。

步骤3非支配排序。计算初始种群的个体目标值，对初始化种群进行快速非支配排序和拥挤度计算。

步骤4二元锦标赛。通过二元锦标赛的方式选择适合繁殖的父代。

步骤5交叉、变异。对步骤4得到的父代分别以Pc和Pm的概率进行交叉和变异操作，获得子代后与父代合并形成新种群。

步骤6非支配排序。对步骤5得到的新种群进行快速非支配排序和拥挤度计算，选择前Ps个体形成新父代种群。

步骤7判断迭代次数。若到达最大代数则输出结果；否则G=G+1，返回步骤4。

4 案例分析

为探究所建的模型与算法的有效性，文中以巴黎RER A线为例进行了验证。RER A是一条东西贯通巴黎市区的铁路，线路图如图1（a）所示，该线具有5个分支，由法国国营铁路公司和巴黎大众运输公司共同经营，整体线路呈现一般树型线的形态，抽象出的拓扑网络如图4所示。文中以由西向东方向，即由分支A1、A2、A3开往分支A4、A5方向为上行方向，反之为下行方向。由于保密限制，难以获得实际的乘客OD信息。因此，文中以每小时0～200的随机数随机生成全线OD需求，用来进行理论分析［13］。结果中的上行方向最大断面客流量为52 396人/h，出现在Auber与Chatelet-Les Halles之间，下行方向最大断面客流量为38147人/h，出现在Nation与Gare de Lyon之间，与实际断面客流量情况基本一致［14］。

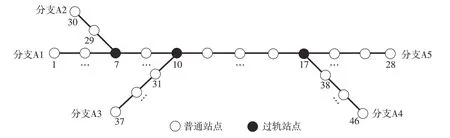
图4 RER A线拓扑结构Fig.4 Topological structure of RER A

4.1 参数选取

结合巴黎RER A线实际情况与相关文献的研究，本研究设置最小发车频率fmin=6列/h，最大发车频率fmax=30列/h。以RER A线大量使用的MI 09型双层列车为参照，设置列车定员C=2 582人［15］，列车平均旅行速度v=15 m/s，折返时间θ=5 min，换乘时间μ=2 min，最大满载率ηmax=100%，列车每公里运营费用α=30元［12］，列车单位时间的折旧费β=240元［12］。参考文献［16］，根据多次试验，NSGA-Ⅱ算法的参数设置为：Ps=100，进化代数G=200，交叉概率Pc=0.9，变异概率Pm=0.1。

4.2 求解结果

确定参数后利用NSGA-II算法求解一般树型线条件的列车开行方案优化模型，得到的帕累托前沿解如图5所示。

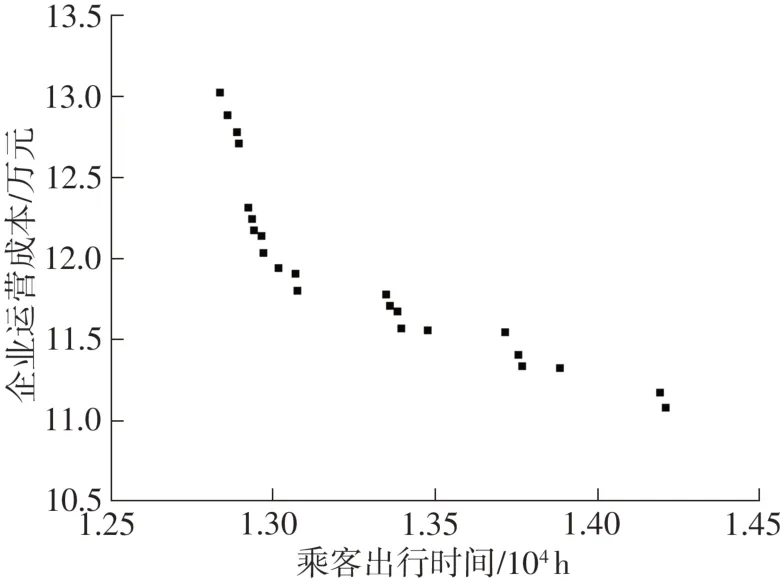
图5 帕累托前沿解Fig.5 Pareto frontier of NSGA-II

由图5可以发现，乘客出行时间与企业运营成本呈现明显的负相关性，且在帕累托前沿解之间，不存在乘客出行时间更小的同时企业运营成本更小的方案。

为了验证文中NSGA-II算法的收敛性，进化过程中各代的平均企业运营成本变化如图6所示。

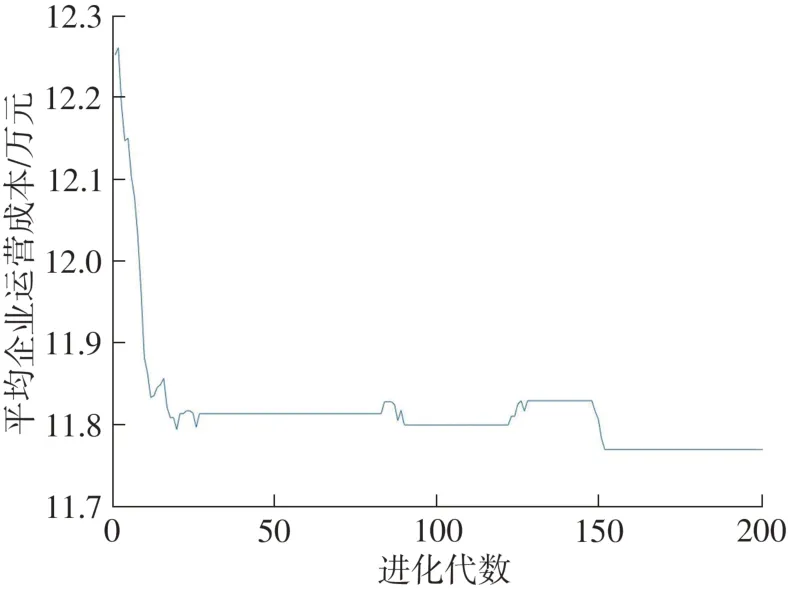
图6 企业运营成本迭代趋势Fig.6 Iterative trend for the operation cost of enterprises

由图6可以看出，平均企业运营成本在前30次迭代时快速下降，迭代150次后趋于稳定，证明算法的收敛性较好。部分帕累托前沿解的优化方案和优化结果如表3所示。

从表3可以发现，优化方案1为乘客出行时间最小的方案，优化方案9为企业运营成本最小的方案。从优化方案1到优化方案9，乘客出行时间逐渐变大，企业运营成本逐渐变小，总列车发车频率逐渐变小，从30对/h降低至27对/h。

同时可以发现，在所有的帕累托前沿解中，有些方案虽然可以满足帕累托最优的条件，但是在实际的运营组织中难以实现，比如表3中优化方案2、5、8。这些优化方案中部分列车的发车频率为7或者11，在多交路列车共线的条件下不能均衡发车，难以进行周期性运行图的编制，会造成极大的能力损失［17］。因此剔除掉这些方案后，得到剩余的6组优化方案，分别为优化方案1、3、4、6、7、9。

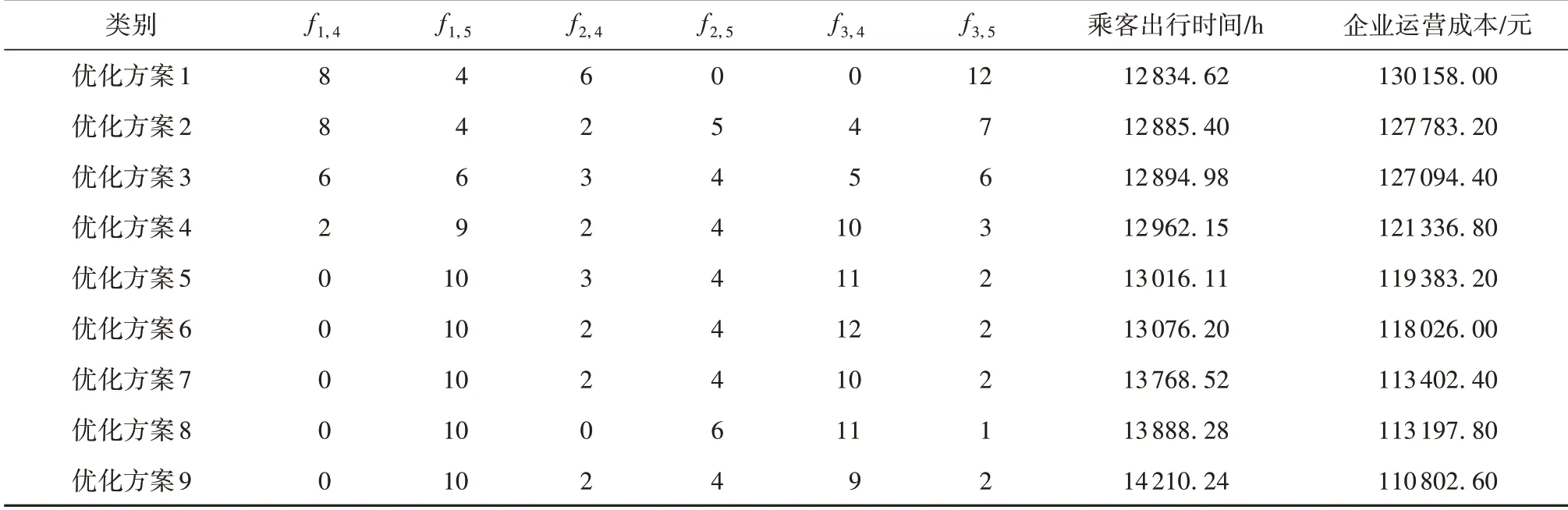
表3 优化方案Table 3 Optimization schemes

由于既有列车开行方案无法获取，难以验证文中开行方案对实际开行方案的改进。因此为体现本研究构建的一般树型线条件下列车开行方案模型的优化效果，将优化方案与分线方案（即干线与支线不过轨运营的方案）进行对比，对比结果如表4所示。

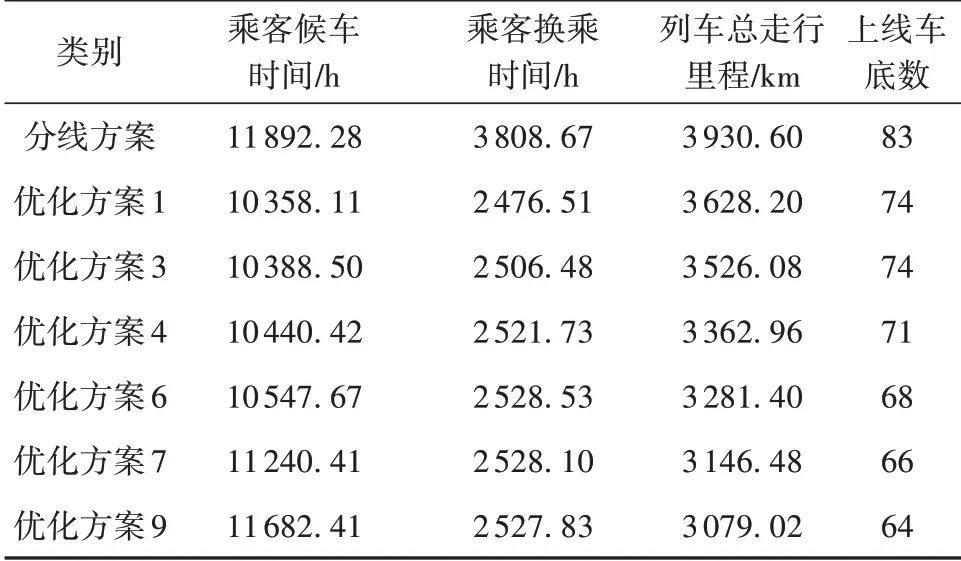
表4 分线方案与优化方案对比Table 4 Comparison of split-line scheme and optimization schemes

由表4可知，所有的帕累托前沿解的方案在各项目标中均显著优于分线方案，乘客候车时间减少了1.76%～12.90%，乘客换乘时间减少了33.63%～34.98%，列车总走行里程减少了7.69%～21.67%，上线车底数减少了9～19列。

5 结语

本研究借鉴既有的Y型线的研究成果，提出了一种全新的线路形式——树型线。树型线是Y型线的进阶形式，同样只拥有一条主干线路，但拥有多条分支从而形成了树的形态。

文中首先设计了一般树型线的线路拓扑形态，并以乘客出行时间与企业运营成本最小为目标函数，构建了一般树型线条件下的列车开行方案优化模型。然后根据所建的多目标非线性整数规划模型，设计了NSGA-Ⅱ算法进行求解，并以巴黎RER A线为例对模型与算法进行了验证。结果表明，算法可求得多个开行方案的帕累托前沿解，乘客出行时间与企业运营成本呈现明显的负相关性。最后，将优化方案与分线运营的方案进行了对比，得到的6个优化方案可使乘客候车时间减少1.76%～12.90%、乘客换乘时间减少33.63%～34.98%，列车总走行里程减少7.69%～21.67%，上线车底数减少9～19列。

文中所构建的一般树型线条件下的列车开行方案假设所有列车都往返于线路末端，后续研究的重点将考虑中间站折返情况，制定更复杂的开行方案应对多样化的客流需求。