考虑出行焦虑的异质小汽车通勤者早高峰出发时刻选择研究

胡郁葱 骆明明 潘雷 凌美宁 卢晓珊

（1.华南理工大学土木与交通学院，广东 广州 510640；2.现代城市交通技术江苏高校协同创新中心，江苏 南京，211189；3.广州市交通运输研究院有限公司，广东 广州 510627；4.广州市城市规划勘测设计研究院，广东 广州 510060；5.合肥工业大学汽车与交通工程学院，安徽 合肥 230009）

早高峰拥堵常发生在道路的瓶颈路段，Vickrey［1］于1969年首次提出著名的“瓶颈模型”，系统性地计算了瓶颈路段的出发率、高峰期起止时刻等指标。在此基础上，众多学者进行了拓展，如戴庆等［2］构造了单一瓶颈的家庭通勤网络，精准地刻画了家庭出行者在活动效用作用下早高峰期间的出发时间选择行为；李超婷等［3］将单一瓶颈拓展为双瓶颈，探讨了模型中双瓶颈需要满足的条件，并分析了家庭出行者的出行行为。但现有研究多是从宏观角度根据实际需要对标准瓶颈模型的固有属性或应用场景进行拓展，并未考虑到通勤者出行心理的影响。根据西蒙［4］提出的有限理性学说，情感、态度及其他非理性因素都会对出行行为产生影响。据此，Eleanor等［5］在出行方式选择中引入情感因素，确定了人们在使用不同出行方式时的情感差异以及这些差异如何影响出行决策；卢珂［6］从感知收益和损失两个角度构建了网约车出行模型，证实了出行者在形成网约车使用意愿过程中社会心理变量的重要作用；Malichova等［7］侧重探究了小汽车通勤者对时间价值和乘车价值的感知如何影响日常通勤时的乘车选择，结果发现满足感在出行感知成本中充当了重要作用。这些成果均从不同角度证明了情感、偏好等非理性因素对出行行为存在影响，都可能是导致出行行为选择差异的重要原因之一。

在众多非理性因素中，焦虑被定义为对预期产生的不良后果或个体感受到威胁时所产生的一种不愉快的情绪体验［8］。在交通领域，频发且持续的道路拥堵易使驾驶员感到烦躁，甚至转变为愤怒情绪［9］。郭峘等［10］发现驾驶时间与焦虑水平呈现正相关，交通堵塞时间越长，焦虑程度就越高；Huang［11］指出不同群体对上班早到和迟到的心理感知也存在差异，且通勤者每日的出行心理并不固定，例如连续多日的瓶颈处拥堵可能会使部分出行者产生不适，进而宁愿选择早到或迟到也要避免遭遇拥堵。这些因素都可能导致部分通勤者对出发时刻进行重新选择。将瓶颈模型应用于缓解拥堵的实践中时，若忽略上述因素，不仅会影响对通勤者出行规律的判断，而且可能会使制定的缓堵政策不能对所有通勤者发挥相同效用，最终导致对政策效果的错误评估。现阶段，城市交通正从强调增加设施供应的发展阶段进入更关注出行者体验的品质提升新阶段［12］，迫切需要在缓堵政策研究中更精细化地考虑非理性因素的影响。

当前已有学者开始探讨这类问题，如吴文祥等［13］讨论了公交车厢拥挤的负面心理感知对早高峰出发率的影响，郭晓［14］基于瓶颈模型探讨了积极出行者和消极出行者对于早到与迟到的不同心理感知。但是当前研究多为间接讨论焦虑情绪，并未将焦虑情绪直接反映到通勤者的出发时刻选择当中，其中的关键问题是如何将驾驶员的焦虑情绪进行量化并融合到瓶颈模型中。

基于此，本研究尝试对标准瓶颈模型进行拓展，首先根据不同小汽车驾驶员群体的出行焦虑偏好，将早高峰通勤者进行分类，然后对焦虑情绪进行量化，并融入到瓶颈模型的出行成本中，分别在单一线路和混行线路下，对两类通勤者的出发率、高峰期起止时刻和数量构成等关键指标进行计算，最后与标准瓶颈模型进行对比，以揭示出行焦虑对小汽车驾驶员出发时刻选择行为的影响。

1 基本假设

为了与标准瓶颈模型［1］进行对比，文中主要研究以上班为目的、有规律的在早高峰出行的私人小汽车通勤者，研究对象分为I类堵车焦虑型和Ⅱ类准点焦虑型：I类通勤者对应现实中收入较高的群体，工作时间灵活，对于能否准点到达并不敏感，而道路上的长时间拥堵更容易使其焦虑；Ⅱ类通勤者对应于蓝白领等工薪阶层，工作时间固定，对道路上的拥堵时长并不关心，而能否准点到达则是该类群体关注的重点。

实际上，通勤者可能同时兼具拥堵焦虑和准点焦虑两种特征，但同一通勤者两种焦虑特征完全对等的情形较为少见，大部分通勤者都存在对某一类焦虑的侧重，本研究将其归入到侧重该类型的焦虑群体中，即假设任一通勤者仅具有一类焦虑特征。

考虑两种连接住宅区O与工作地D，并仅由小汽车提供出行的简易线路（见图1）。图1（a）中单一线路在现实中并不存在，设置该情形是为了分别探究两类通勤者自身的出行特征，此时道路上仅存在某一类通勤者；图1（b）的混行线路更接近实际，此时两类通勤者在道路上同时存在。设早高峰总通勤人数为N，由I类、Ⅱ类通勤者人数N1、N2组成，高峰期内瓶颈路段满负荷运行。

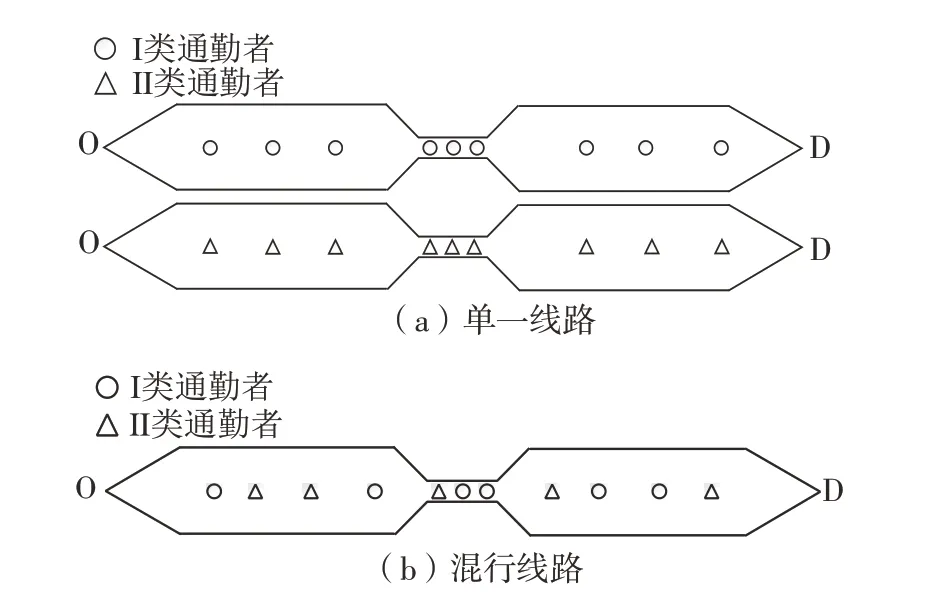
图1 两种简化线路Fig.1 Two types of simplified lines

定义文中相应的量符号及其含义如表1所示。

表1 符号定义Table 1 Mathematical symbol definition

两类通勤者的特征定义如表2所示。

表2 异质通勤者特征Table 2 Attributes of heterogeneous commuters

在构建两类通勤者的出行成本函数之前，给出以下假设：

（1）通勤者属于I类或Ⅱ类未定，这取决于其当日的出行焦虑偏好，偏好决定后，就被归入该类通勤者，不再考虑另一种焦虑偏好；

（2）为简化分析，设通勤者从住宅区O出发后就开始经历瓶颈拥堵并在离开瓶颈后直接到达工作地D，即自由行驶时间为0；

（3）文献［14］中对于早到与晚到通勤者的感知效应系数取值范围为0＜k2＜β，文中沿用以上假设，文献［1］指出γ＞α＞β，表明迟到代价高于道路拥堵代价，因此假设对于通勤者整体而言，由不准点到达所导致的单位焦虑时间成本相对要大于由道路拥堵延误所造成的单位焦虑时间成本，即k2＞k1；

（4）两类通勤者的工作开始时刻t*相同。

2 考虑心理焦虑的出行成本函数

I类通勤者出行成本由瓶颈拥堵延误成本、不准点（早到或迟到）延误成本、实际瓶颈拥堵时间ω(t)超出（低于）心理预期拥堵时间μω(t^)的出行焦虑（满足）成本组成，ω(t)-μω(t^)＞0时产生出行焦虑，ω(t)-μω(t^)＜0时产生心理满足，t时刻出发的I类通勤者出行成本为

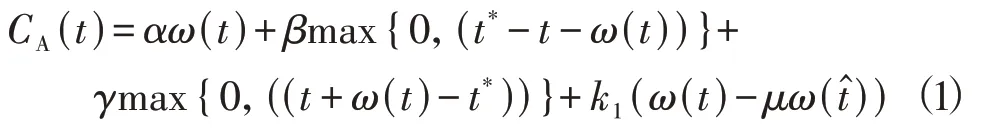
式中，t*＞t+ω(t)表示I类通勤者早到，反之表示迟到，以下类似。

Ⅱ类通勤者出行成本由瓶颈拥堵延误成本、不准点延误成本、迟到（早到）所产生的心理焦虑（满足）成本组成，t+ω(t)-t*＞0时产生心理焦虑，反之产生心理满足，t时刻出发的Ⅱ类通勤者出行成本为

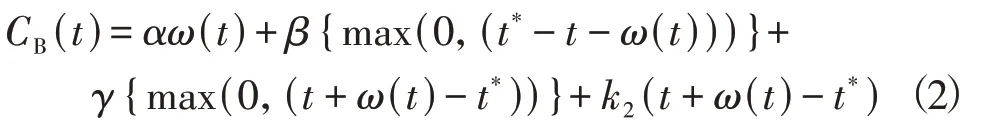
利用效用值问卷调查可得到某一城市或区域的堵车焦虑系数k1、准点焦虑系数k2及瓶颈忍耐系数μ的具体数值，然后可计算通勤者不同出发时刻下的成本并进行类型划分，如图2所示。

图2 通勤者划分Fig.2 Division of commuters

3 模型

3.1 通勤者处于单一线路时

（1）道路上仅有I类通勤者时，高峰期瓶颈满负荷运行，因此I类通勤者的高峰期长度为

根据标准瓶颈模型［1］，最早与最迟出发的通勤者无需排队，且交通流平衡时，所有I类通勤者的出行成本相同，有CA(tAs)=CA(tAe)，化简为

定义在t^A时刻出发的通勤者刚好能在工作开始时刻t*到达工作地，故：

联立式（3）-（5），解得：

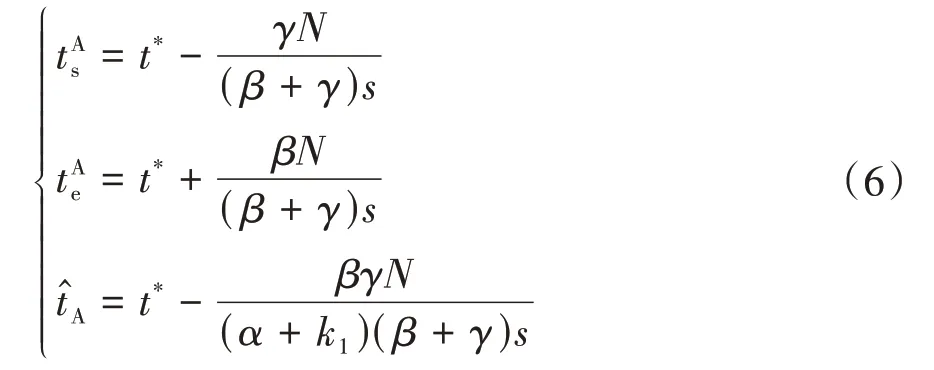
将式（6）代入式（1），得到I类通勤者的平衡出行成本CA为

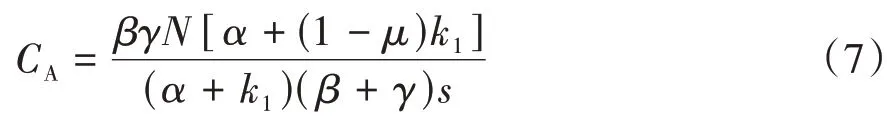
（2）道路上仅有Ⅱ类通勤者且交通流平衡时，所有通勤者的出行成本相同，最早与最迟出发的通勤者不经历排队；t^B时刻出发的通勤者刚好能在时刻t*到达工作地；高峰期瓶颈处满负荷运行，根据以上条件求得：

将式（8）的结果代入式（2），则Ⅱ类通勤者的平衡出行成本CB为

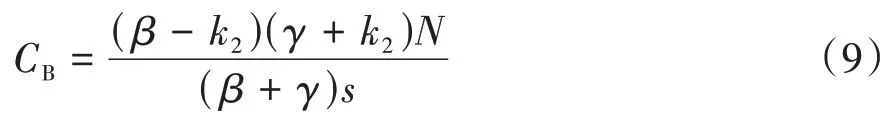
图3给出了单一线路中不同类型通勤者的拥堵延误时间，X轴是通勤者出发时刻，Y轴是通勤者经历的拥堵延误时间，t^A时刻或t^B时刻出发的通勤者会遭遇最长拥堵时间［1］。

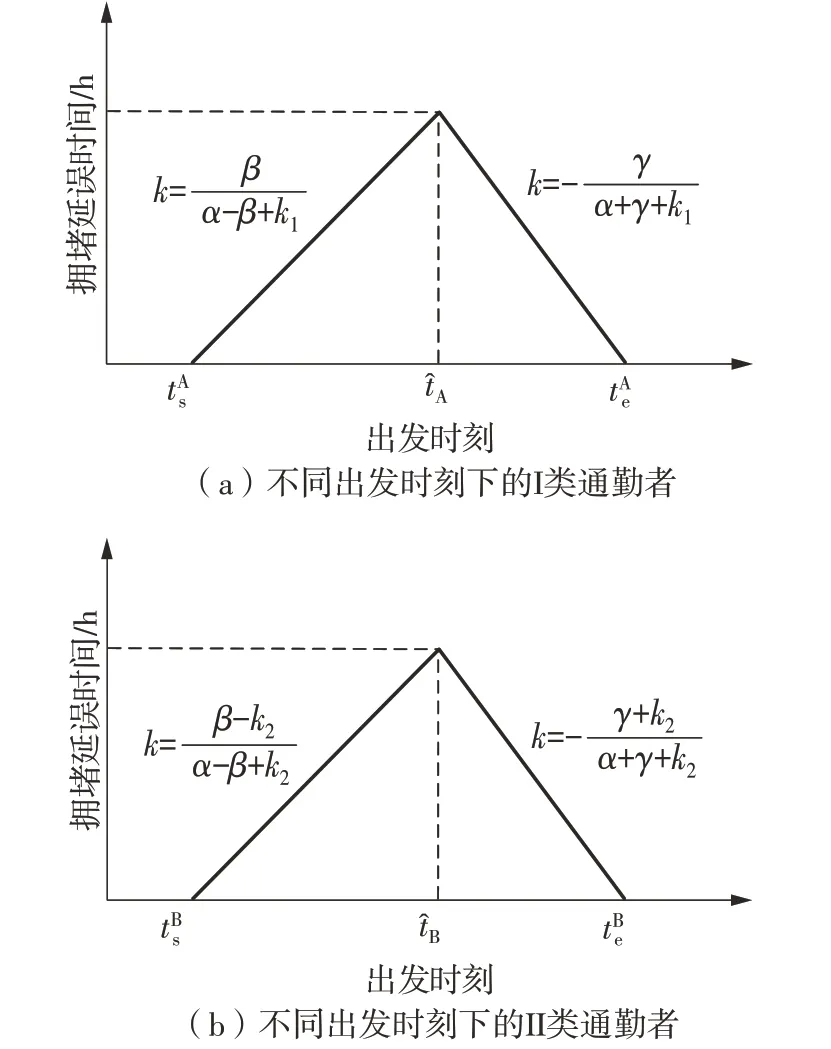
图3 单一线路的通勤者拥堵延误时间Fig.3 Congestion delay of commuters on a single line

3.2 通勤者处于混行线路时

3.2.1 混行线路下的模型性质

对于两类通勤者混合出行的情形，可得到以下性质。

性质1Ⅱ类通勤者总比I类通勤者先出发，即

证明：利用反证法，首先假设tBs≥tAs（见图4），时刻混行线路上只存在I类通勤者（极端点处tAs、重合），满足条件CA(tAs)≤CB(tAs)，即k2(t*-tAs)-另外至少存在一个时刻t′处于[tBs，tAe]（极端点处t′=tBs=tAe），此时道路上同时存在两类通勤者，因此有CA(t′)=CB(t′)，得到k2(t*-tAs)-根 据 前 述 假设k2＞k1和条件产生矛盾，性质1得证。

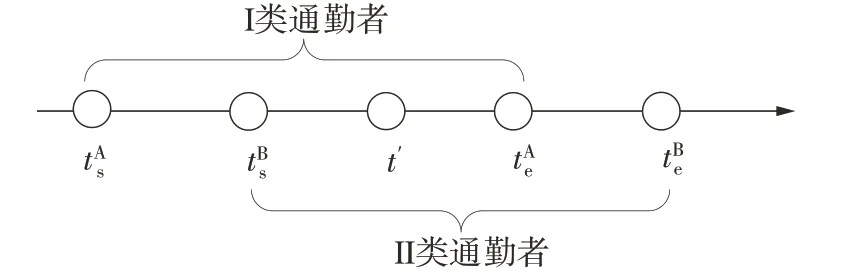
图4 I类通勤者比Ⅱ类通勤者先出发的假设情形Fig.4 Hypothetical situation where commuters of group I depart earlier than commuters of groupⅡ

性质2两类通勤者出行高峰期不重叠。

证明：利用反证法（见图5），时刻t^左侧为早到区间，右侧为迟到区间，假设灰色重叠区域位于早到区间，重叠区域内任取时刻t1、t2且t2＞t1。

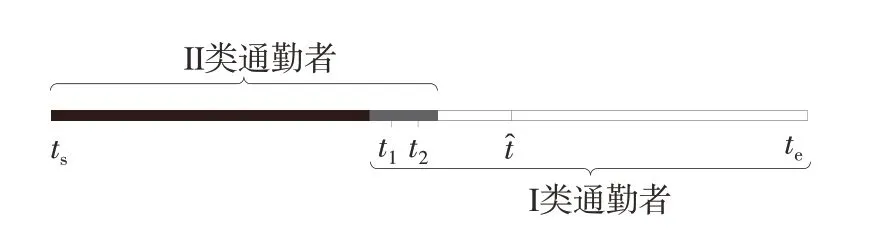
图5 重叠区域位于早到区间Fig.5 Overlapping area is in the early period

重叠若存在则必然满足CB(t1)=CB(t2)=CA(t1)=CA(t2)，t1、t2时刻出发的通勤者成本经计算并化简后可表示为

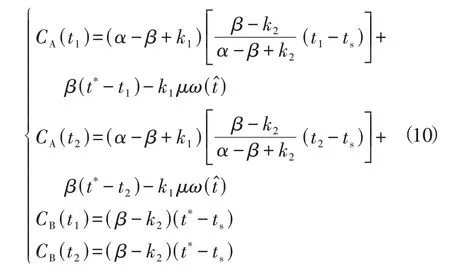
CB(t1)=CB(t2)显然成立，若CA(t1)=CA(t2)，则化简后有k2α=k1(β-k2)，而根据条件0＜k1＜k2＜β＜α，显然有k2α＞k1(β-k2)，矛盾，因此重叠区域不会位于早到区间，类似可证明重叠区域也不会位于迟到区间，性质2得证。

3.2.2 混行线路情景

由上述性质可知混行线路中Ⅱ类通勤者总比I类通勤者先出发，且高峰期不重叠，故讨论以下两种混行情景。

（1）混行情景1

Ⅱ类通勤者全部位于早到区间，I类通勤者全部位于迟到区间，最大延误时刻t^1刚好与两类通勤者的高峰期分割点t1d重合，如图6所示。

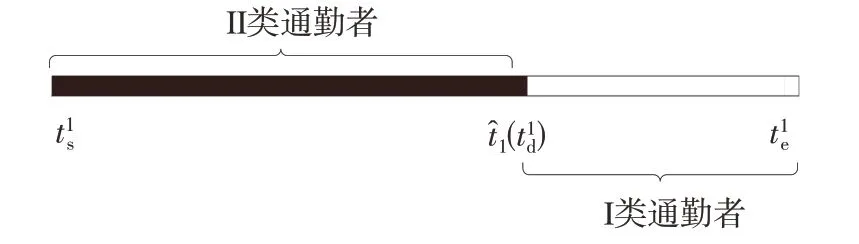
图6 混行情景1Fig.6 Mixed situation 1

对混行情景1的广义出行成本函数求偏导［1］，求得早高峰出发率为

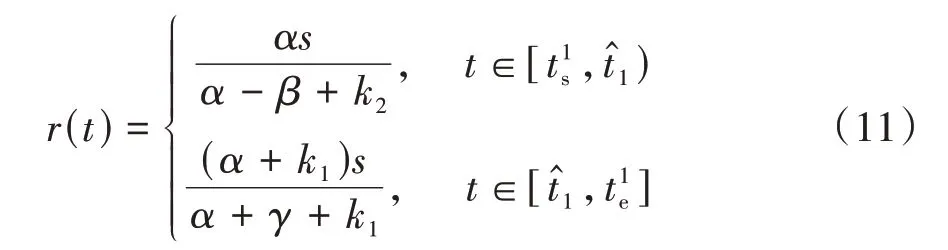
设Ⅱ类通勤者的数量占比为θ2，其数量也可用上述出发率表示为

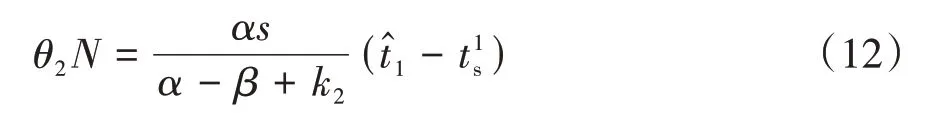
交通流达到平衡时，两类通勤者在时刻的瓶颈等待时间相同，且所有通勤者出行成本相同，有CB(t1s)=CA(t1e)；定义时刻出发的通勤者刚好能在工作开始时刻t*到达工作地，以上条件结合式（12），解得：

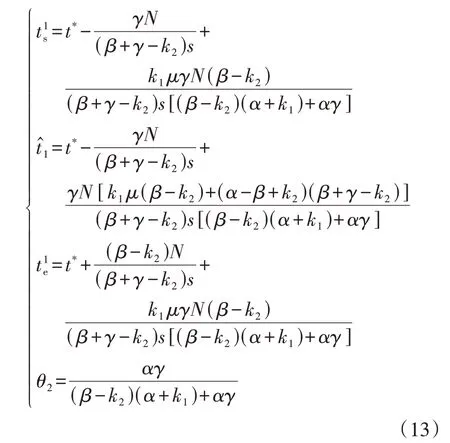
根据式（13）求得混行情景1下的通勤者平衡出行成本为

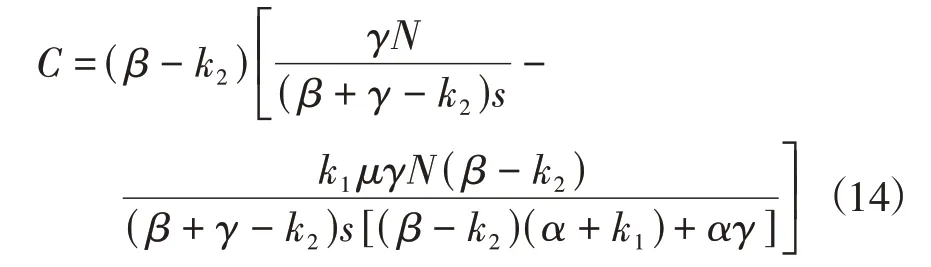
（2）混行情景2

Ⅱ类通勤者跨早到与迟到区间，I类通勤者仅位于迟到区间，两类通勤者高峰期分割点为，此时＞，如图7所示。

图7 混行情景2Fig.7 Mixed situation 2

类似求得混行情景2下的出发率为

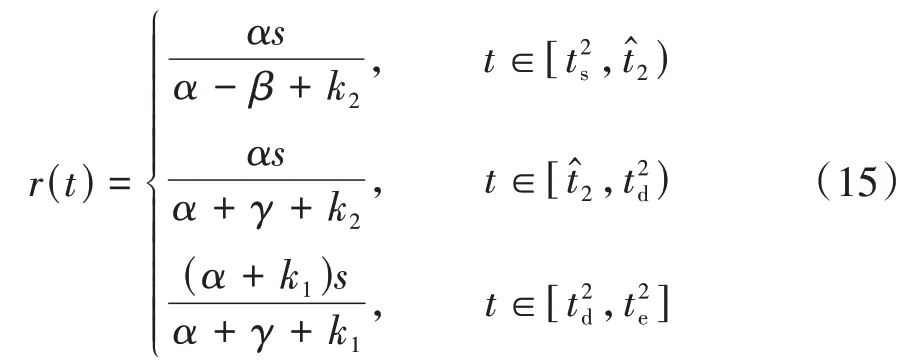
设混行情景2下的Ⅱ类通勤者占比为θ′2，则I类通勤者数量用出发率表示为

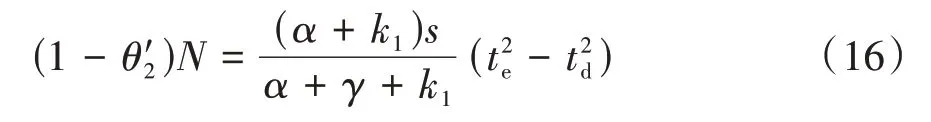
早高峰长度与总通勤人数N有关；定义时刻出发的通勤者刚好在时刻t*到达工作地；平衡时所有通勤者出行成本相同，有CB(t2s)=CB(t2d)，解得：

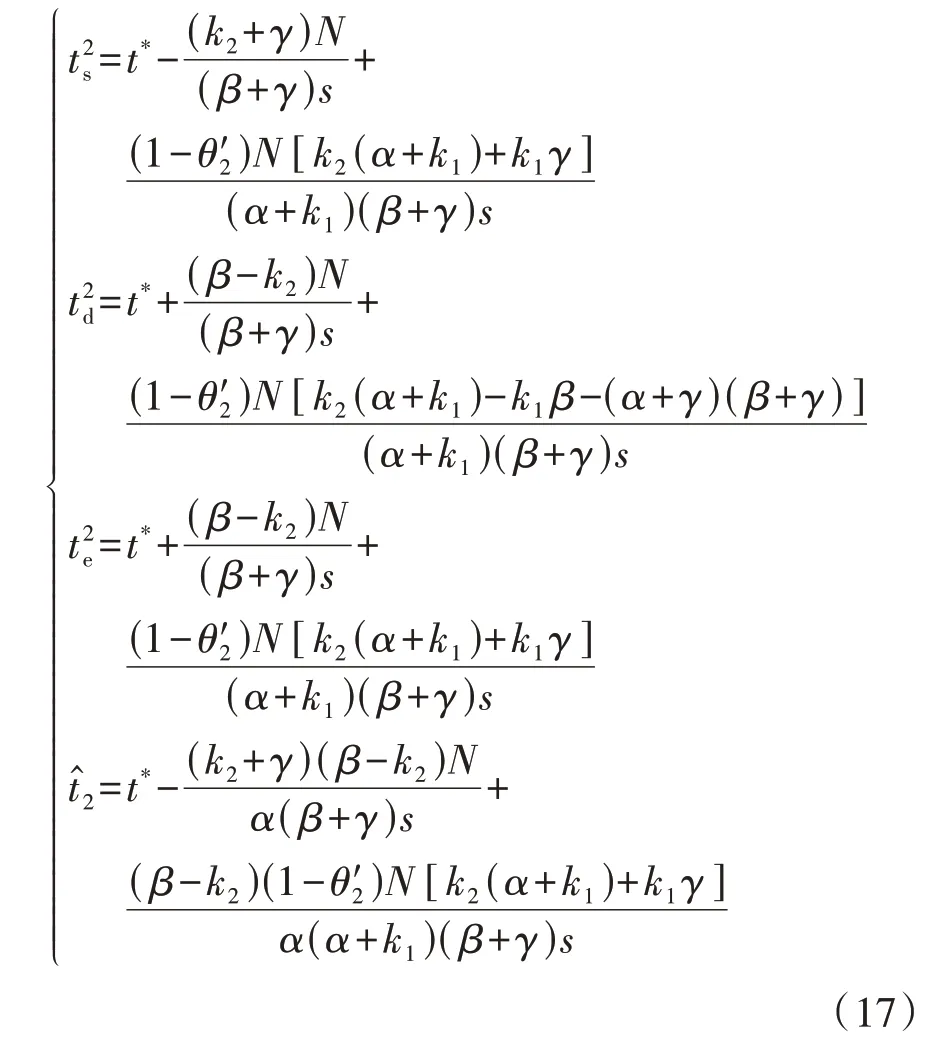
根据式（17）求得含参数θ′2的I类通勤者的平衡出行成本C1为

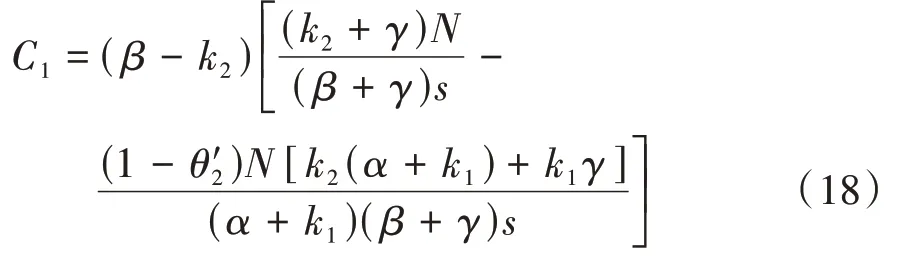
同理，可求得含参数θ′2的Ⅱ类通勤者的平衡出行成本C2为

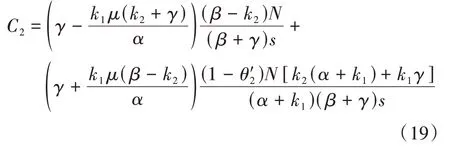
显然，交通流平衡时通勤者出行成本相同，有C1=C2，解得参数θ′2为

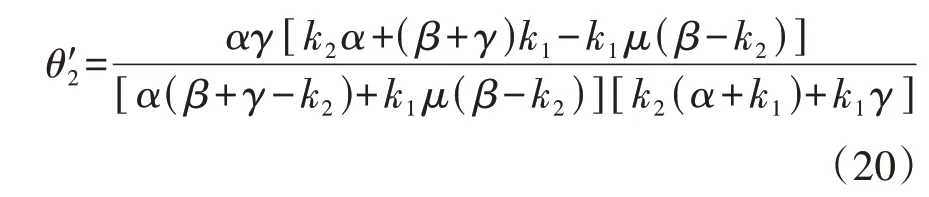
图8展示了两种混行情景下的通勤者拥堵延误时间与出发时刻的关系，或时刻出发的通勤者有最长拥堵延误时间。

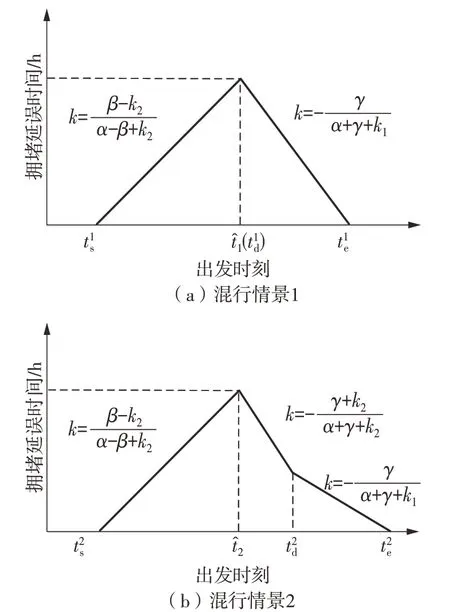
图8 两种混行情景下的通勤者拥堵延误时间Fig.8 Congestion delay of commuters under two mixed situations

3.2.3 与标准瓶颈模型（SBM）的对比

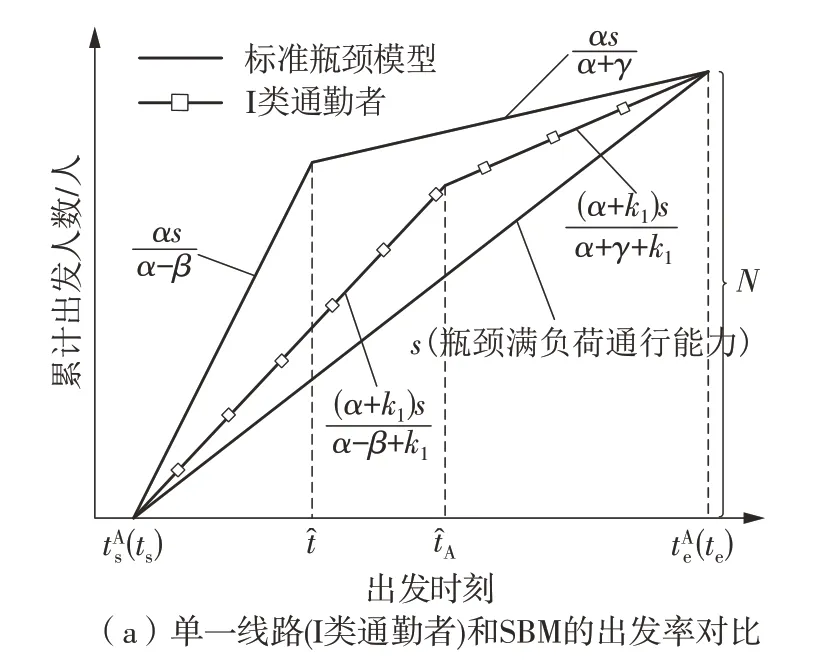
图9给出了两类通勤者在单一线路和混行线路中与标准瓶颈模型（SBM）的出发率对比的结果，Y轴表示累计出发的通勤者人数，斜率指通勤者出发率。

图9（a）、9（b）说明，道路上仅有I类通勤者时，高峰期对比SBM并未提前或延后；仅有Ⅱ类通勤者时，高峰期相较于SBM更早发生（前移），符合Ⅱ类通勤者倾向于早出发的特征。

由图9（c）可以看出，混行情景1与SBM相比，高峰期更早发生（前移），说明考虑了焦虑情绪后，通勤者整体趋向于早出发。

混行情景2高峰期也同样发生前移，见图9（d），与混行情景1不同的是，其出发率被划分成三部分。相较于SBM，混行情景2的通勤者在时段的出发率更大。

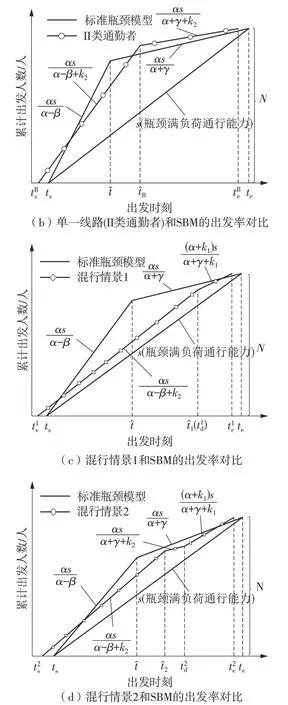
图9 不同出行场景与标准瓶颈模型的出发率对比Fig.9 Comparison of departure rates between different travel situations and standard bottleneck model

4 关键参数的获取方式

对参数k1、k2和μ，拟采用效用值问卷调查确定不同城市或区域的参数取值，n1为划分的预留拥堵时间的等级，例如划分为0～5min、5～10min等若干个等级，ωi为问卷调查中不同划分等级下的I类通勤者的预留拥堵时间期望值，q(ωi)为不同划分等级下的通勤者比例，瓶颈忍耐系数μ可表示为

令n2、n3分别为两类通勤者下划分的焦虑成本占比早通勤总出行成本的若干个等级，mi、pi指的是I类、Ⅱ类通勤者的通勤焦虑成本在早通勤总成本上的占比期望值，q(mi)、q(pi)为不同类型的通勤者比例，例如对于I类通勤者而言，认可堵车焦虑成本在早通勤总成本的期望占比为mi的通勤者比例为q(mi)，ccommuter为该城市或区域的小汽车平均早通勤成本，通过下列公式计算的系数k1、k2即为某一城市或区域的平均水平。

实际上，通过设计不同形式的调查问卷可以对以上参数不断进行修正，最终得到适合该城市或区域的更为精确的参数值。

5 数值算例

根据前述假设以及郭晓［14］、Small［15］等的参数设置，表3给出主要参数的取值。

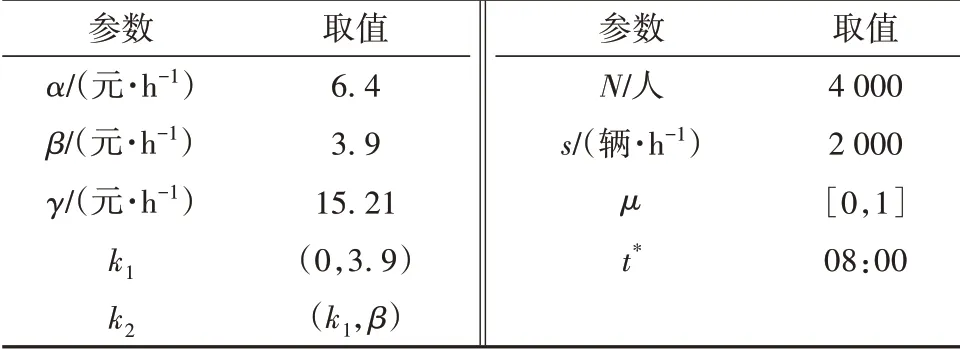
表3 参数取值Table 3 Parameter values

5.1 单一线路结果分析

单一线路的系统总感知出行成本随参数变化的结果如图10所示。

图10（a）中，道路上仅有I类通勤者，堵车焦虑系数k1越大，系统总感知出行成本就越小，且随着瓶颈忍耐系数μ的增加，出行感知成本进一步减小，这是因为当通勤者对瓶颈拥堵延误的焦虑程度提高时，通勤者会选择更有利的出发时刻以进一步降低自己的出行感知成本，同时随着通勤者对于瓶颈处预留的拥堵时间越来越充足，拥堵对于通勤者造成的负面感知成本也会进一步降低。

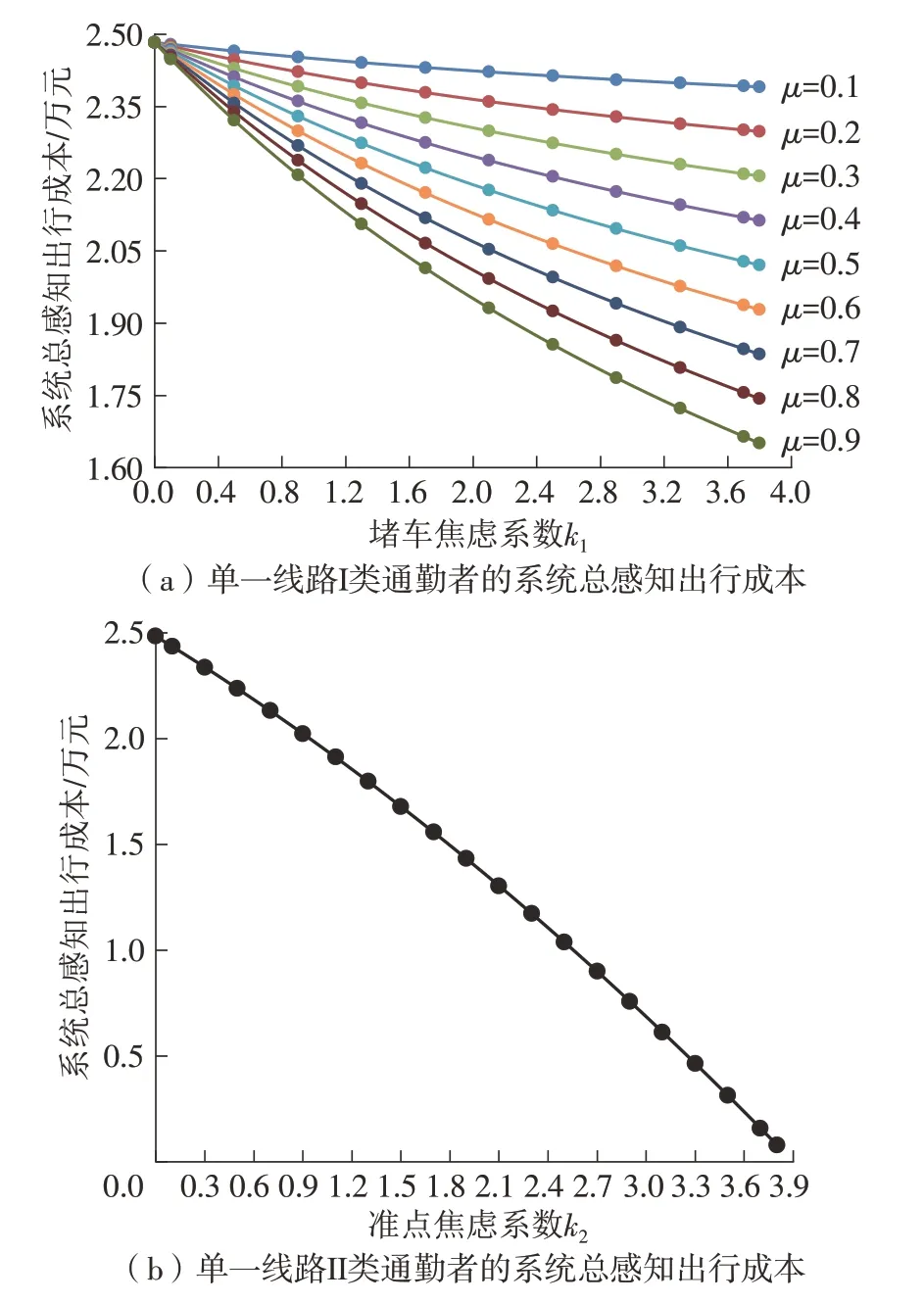
图10 单一线路系数改变时的系统总感知出行成本Fig.10 Total perceived travel cost of system when coefficients changes under a single line

图10（b）中，道路上仅有Ⅱ类通勤者，准点焦虑系数越大，通勤者同样会选择更有利的出发时刻，导致系统总感知出行成本的进一步降低。

5.2 混行线路结果分析

5.2.1 系统总感知出行成本

两种混行情景的系统总感知出行成本随参数变化的结果如图11所示。

由图11可见，准点焦虑系数k2对于系统总感知出行成本的影响较大，k2越大，出行成本就越低。

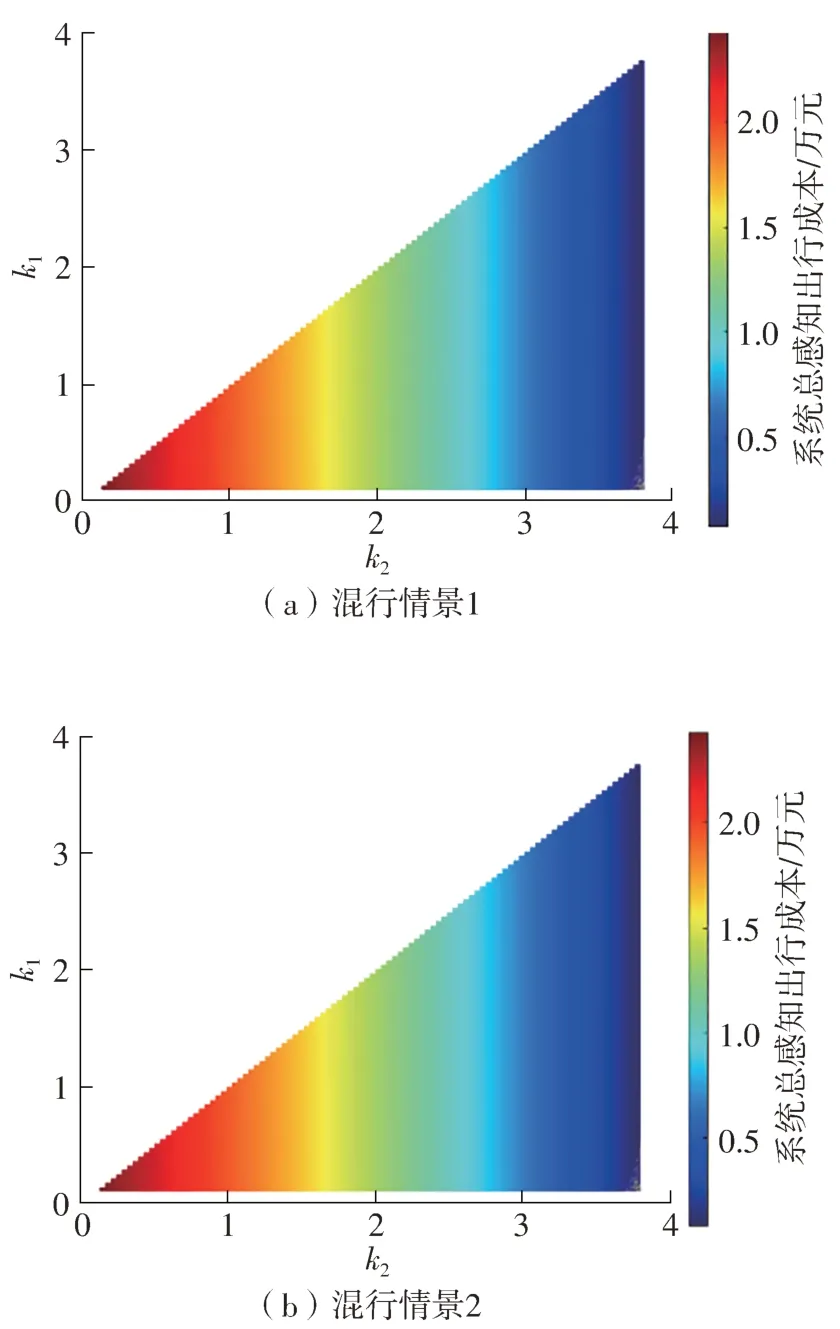
图11 两种混行情景的总感知出行成本Fig.11 Total perceived travel cost of two mixed situations

5.2.2 通勤者分布

图12（a）描述了混行情景1的通勤者分布，根据式（13）可知通勤者分布与μ无关，仅与系数k1、k2有关。显然，k2越大，通勤者对不准点延误越重视，Ⅱ类通勤者群体数量就越多；k1越大时，通勤者对拥堵延误就越焦虑，I类通勤者群体数量也会少量增加。单位转移数量的不同说明系数k2在通勤者分布中的影响更大。

图12（b）显示混行情形2中k2越大，Ⅱ类通勤者数量同样越多。图12（c）则进一步说明混行情形2中系数k1和μ对通勤者分布的影响有两面性，如取k2=2.2，μ取较小值（如μ=0.1）时，随着k1的增加，I类通勤者数量反而单调减少，在μ较大时（如μ=1.0），随着k1的增加，I类通勤者数量单调增加，图中“转折线”由不同忍耐系数（μ）下的“先减后增”曲线的拐点组成，“转折线”下方递减，上方递增，原因是μ较大时I类通勤者心理预留的瓶颈拥堵时间较充足，此时若k1增大，通勤者收益进一步提高，所以会提升I类通勤者群体的吸引力，而μ较小时通勤者心理预留的瓶颈拥堵时间不足，k1增大时，损失进一步加剧，反而会降低I类通勤者群体的吸引力。不同μ与k1的组合下，该类群体的吸引力呈现单调减小、先减后增和单调增加三种趋势。

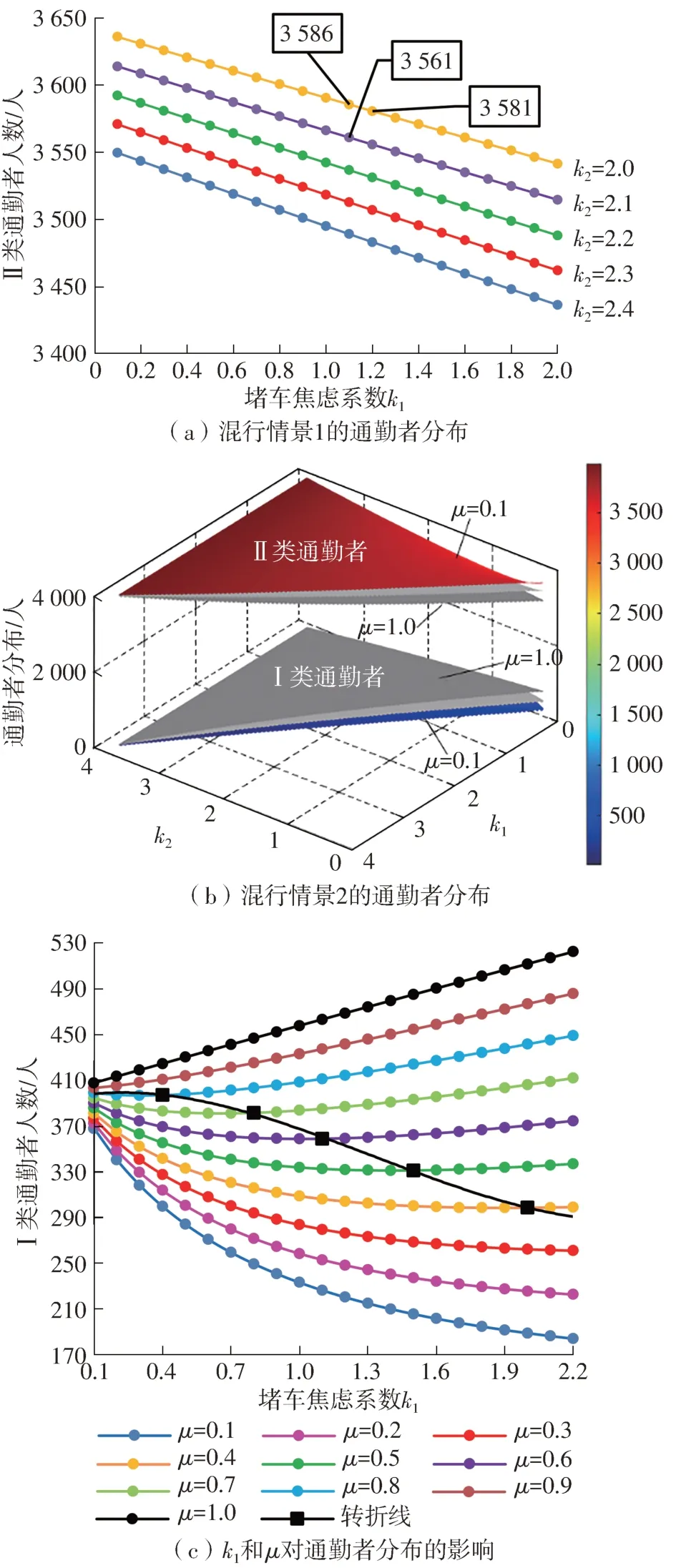
图12 两种混行情景的通勤者分布Fig.12 Distribution of commuters in the two mixed situations

5.2.3 高峰期移动趋势

两种混行情景的最早出发时刻如图13所示。由于混行线路中高峰期长度固定，图13（a）、13（b）中最早出发时刻的变化即代表高峰期整体移动的趋势，明显看出其主要取决于系数k2与μ，k2越大，Ⅱ类通勤者数量越多，该类群体早到获得出行收益，而迟到遭受焦虑损失，因此Ⅱ类通勤者会尽量早出行以避免产生负面成本，使得高峰期更早发生（前移）；μ越大时，通勤者预留的瓶颈拥堵时间越多，I类通勤者趋向于更晚出发以获得最大收益，导致早高峰延后发生（后移）。

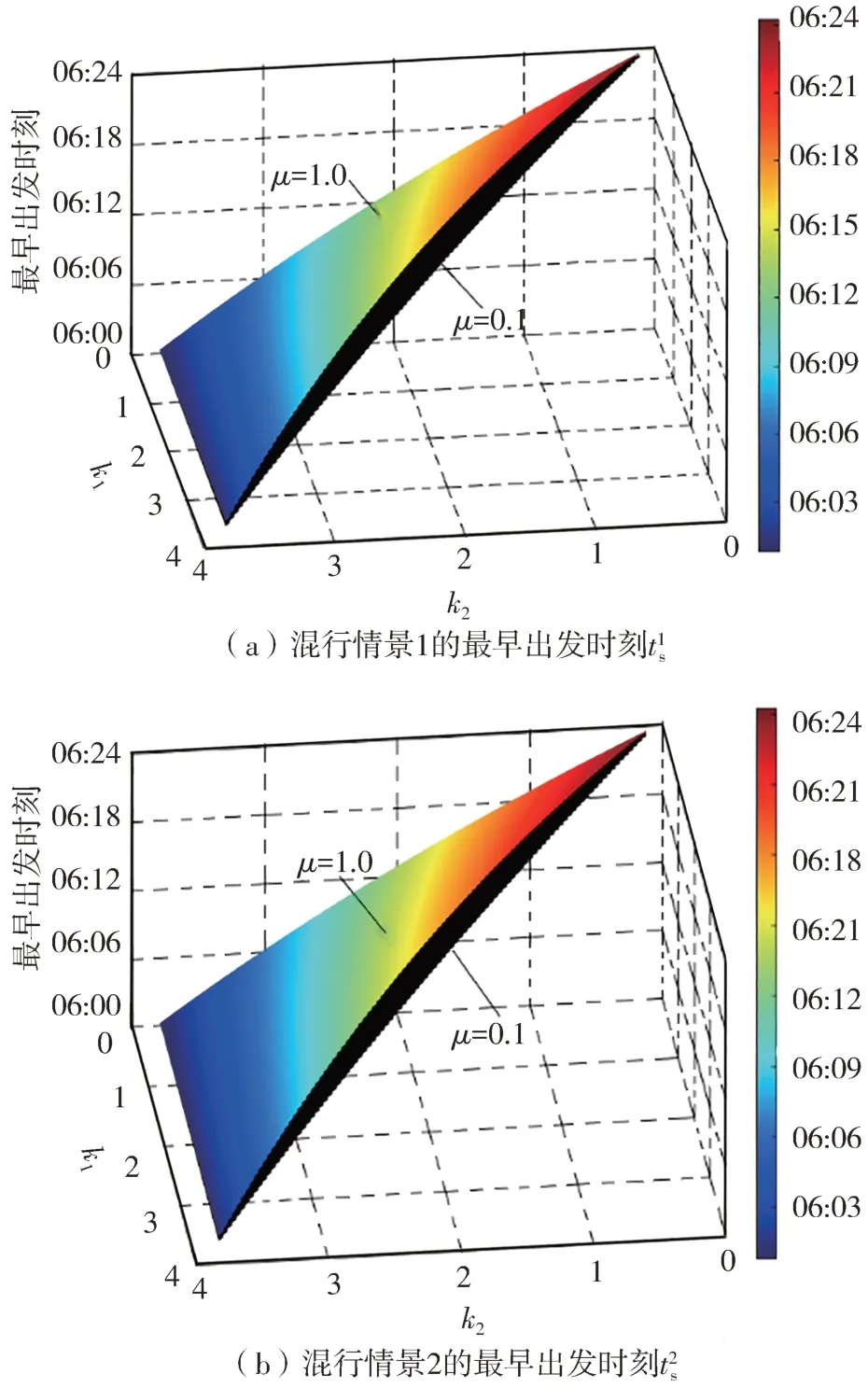
图13 两种混行情景的最早出发时刻Fig.13 Earliest departure time in the two mixed situations

5.3 对管理策略的影响

5.3.1 系统总感知出行成本引导策略

图11的结论启示我们，通过导向性的政策宣传，提升通勤者对准点上班的重视程度（准点焦虑系数k2），能有效降低系统总感知出行成本。例如，混行情形2中，当k1取0.5，通勤者的准点焦虑系数k2由0.6增加到3.8时，系统总感知出行成本就从21663元降至795元。

5.3.2 通勤者分布调节策略

管理者在高峰期安排更多的交通疏导力量，提升缓解道路拥堵的服务水平，增强通勤者对于拥堵尽快消散的信心，这将减少通勤者对于瓶颈拥堵的心理预留时间（瓶颈忍耐系数μ）。

在混行情形2中，若固定系数k2=2.2，k1=2.1，当提升道路服务水平使得瓶颈忍耐系数μ从0.9降为0.1时，I类通勤者人数就从186增加到517。

5.3.3 高峰期移动趋势调节策略

通过政策引导性宣传提升（降低）通勤者对于准点上班的重视程度（系数k2），可以控制高峰期提前（延后）发生，如混行情景1中μ取0.5，k2从0.1增加到3.8时，t1s就从06：24提前至06：01，导致高峰期提前发生。

而减少高峰期的交通疏导力量，降低瓶颈处服务水平会增加通勤者对于瓶颈拥堵的心理预留时间（瓶颈忍耐系数μ），如混行情景2中，k2取2.0，μ从0.1提升到1.0时，t2s就从06：14延后至06：17，促使高峰期延后发生。

6 结语

在标准瓶颈模型的基础上研究了I类堵车焦虑型和Ⅱ类准点焦虑型小汽车通勤者的早高峰出发时刻选择行为。结果表明：当道路上仅有某一类通勤者存在时，堵车焦虑系数、瓶颈忍耐系数以及准点焦虑系数的增加，均会使得通勤者重新选择出发时刻以进一步降低自己的出行成本；两种通勤者混行情景中，系数k2越大，Ⅱ类通勤者数量就越多，系统总感知出行成本越小，高峰期也会更早发生（前移），系数μ越大，系统总感知出行成本同样越小，但高峰期会后移；混行情形2中还发现系数μ和k1对I类通勤者数量的影响具有两面性。以上结论在一定程度上揭示了焦虑情绪影响通勤者出发时刻选择的机理，可以帮助管理者根据不同通勤者的出行心理特性，精细化研究治堵措施，同时正确评价政策实施效果，并在此基础上寻找更优的拥堵缓解政策，进一步改善通勤者的出行体验。