弧形类蜂窝芯层面外等效力学性能研究

殷圣地，汤双清，李响*,,2，仇琨，段宇，陈涛

弧形类蜂窝芯层面外等效力学性能研究

殷圣地1，汤双清1，李响*,1,2，仇琨1，段宇1，陈涛1

（1.三峡大学 机械与动力学院，湖北 宜昌 443002； 2.石墨增材制造技术与装备湖北省工程研究中心（三峡大学），湖北 宜昌 443002）

为提高蜂窝结构面外承载能力，从创新设计角度，提出一种弧形类蜂窝夹芯结构，并对其面外力学性能进行研究。首先，采用胞元理论对弧形类蜂窝夹芯结构进行简化，运用材料力学的知识并结合能量法，推导其面外等效模量解析表达式。然后，将弧形类蜂窝芯层结构与传统蜂窝芯层结构进行对比，在相同等效密度下，通过具体数据验算，发现弧形类蜂窝芯层的面外剪切模量有显著地提高。同时，推导出双壁厚弧形类蜂窝面外等效模量表达式。最后，运用数值模拟分析，得到该结构的仿真值，经过理论值与仿真值对比，发现两者相对误差在10%之内，证明推导出的面外等效模量理论公式的准确性。

弧形类蜂窝夹芯；面外等效模量；能量法；数值模拟

夹层结构材料具有轻质高强的优点，在航空航天、船舶等领域中有着极其重要的应用价值。随着国内外学者的不断探索，近年来，国内外许多学者致力于新型蜂窝结构究，并取得了较大的进展，广泛地应用于工程。

随着工程技术不断地提高，传统蜂窝逐渐不能满足部分特殊工况的要求，研发新型蜂窝结构成为热点。经国内外研究学者不断探索，提出了许多新型蜂窝结构[1-4]。Simone DelBroccolo等[1]将内凹六边形和正六边形这两种不同的蜂窝结构进行交替排布，得到一种混合零泊松比蜂窝阵列结构。并通过压缩实验可知该结构在面内刚度不变的前提下，其抗压强度提高了2倍。即在不降低结构变形能力的前提下，提高了结构的承载能力。JosephN Grima等[2]在原有六边形蜂窝的基础上对其进行改进，得到了一种拉胀六角蜂窝结构，发现该结构在面外的杨氏模量要远大于水平方向，并且可以产生具有圆柱形曲率的弯曲变形。王玮[3]通过遗传算法对八边形蜂窝进行改进，得到一种新型八边形蜂窝，并对其推导等效力学性能，通过仿真验证该结构对比原结构在一定程度上减小了应力的集中。蒋伟[4]等人通过对蜂窝进行改进，获得一种负泊松比的蜂窝结构，得到一种环形蜂窝，并推导出该结构等效弹性模量。

目前，对新型蜂窝芯体的力学性能研究最有效的方法是理论分析、实验测试和数值模拟相结合以得到正确的等效力学性能参数公式[5-18]。沈建邦等[5]在环形蜂窝[4]结构的基础上，提出了一种具有负泊松比效应的可变弧角曲边内凹蜂窝结构，利用能量法给出了曲边内凹蜂窝结构的面内横纵向等效弹性模量和等效泊松比的解析公式，该结构在不同的几何尺寸的条件下，得到其等效弹性模量随着尺寸变化而变化的结论。李响等[6-8]通过六边形蜂窝结构的基本单元的优化排列，得到类蜂窝结构，对该结构及夹层结构进行力学性能进行推导与特性分析及优化，通过数值模拟对理论值进行验证，验证具有可靠性。周星驰等[9]从应力与应变的角度并运用能量法对圆形胞元蜂窝芯层面外剪切模量进行公式推导，结合实验与仿真验证其面外剪切模量公式正确性。吴建均[10]等人基于材料力学中材料的连续性、小变形等基本假设，推导出泡沫纹复合夹芯结构的等效弹性常数。对于面外等效剪切模量，kelsey等[11]利用单位力法和单位位移法求解六边形蜂窝芯子的上限与下限。Gibson等[12]给出了等壁厚蜂窝结构面外参数。赵剑等[13]则通过最小势能原理与最小余能原理，得到与kelsey结果同样的上下限。富明慧等[14]则在上述基础上，通过位移边界条件求得的上限与kelsey结果下限一致，同样给出了等壁厚与双壁厚六边形蜂窝芯层面外剪切模量的确定值。王梁等[15]通过有限元软件ABAQUS分析不同的几何尺寸的X型蜂窝芯层，并得到该结构受外夹角的影响最大，蜂窝芯层等效弹性模量与泊松比效应模量随着外夹角增大而增大。齐佳旗等[16]在低速载荷下冲击CFRP蒙皮－铝蜂窝夹层结构，使用有限元软件ABAQUS对该结构进行仿真，实验结果与仿真结果相似，验证其仿真具有准确性。

经过上述文献，可得国内外研究学者为蜂窝芯层结构做出了重大的贡献，为后来者提供了多种研究方法，但对于圆弧形蜂窝力学性能的研究却是极少，本文通过创新构型的角度，构建弧形类蜂窝芯层结构，基于能量法从应变的角度推导该结构面外等效模量，利用数值模拟验证面外等效模量理论公式的正确性，对弧形类窝芯层结构研究提供理论基础。

1 弧形类蜂窝夹芯结构设计

夹层结构分别由上下面板、蜂窝夹芯组成。夹芯在该结构中主要用于承载剪切力，能够较好地抵抗横向剪切力引起的变形。本文从创新构型角度出发构建弧形类蜂窝夹层结构。通过弧线单元与直线单元的优化排列，得出图1所示结构。为了进一步深入研究，该结构单胞的几何参数进行表示为：四个边长长度为，四个弧形的外径、内径分别为、，四个弧长的的圆心角都为1，边长与水平的角度为2，垂直于坐标系，平面的新型蜂窝的厚度为，如图2所示。

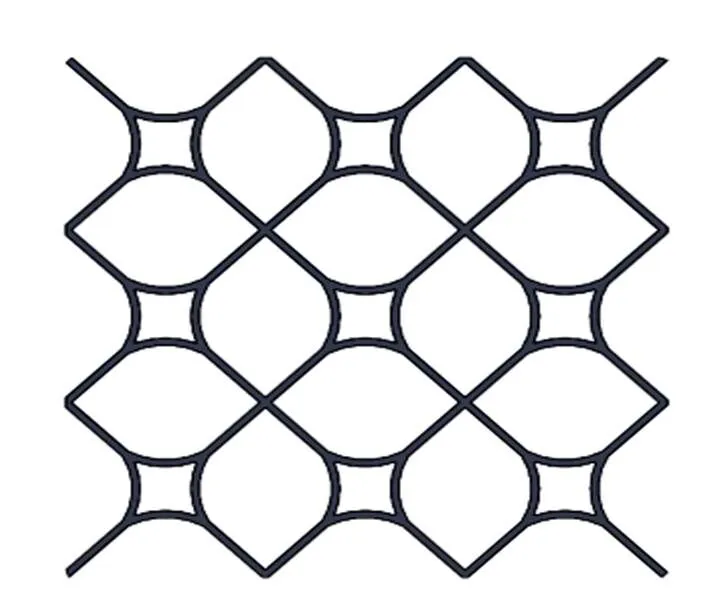
图1 弧形类蜂窝芯层结构

图2 弧形类蜂窝芯层尺寸参数

2 弧形类蜂窝夹芯面外力学特性分析

2.1 等壁厚弧形类蜂窝夹芯结构面外等效弹性模量

由于蜂窝芯层结构作为多孔结构的典型代表，是一种不连续、不均质的面板。为了进一步研究蜂窝芯层结构力学性能，根据胞元理论将弧形类蜂窝芯层简化，推导等效模量理论公式，蜂窝芯层结构等效模量主要分为面外等效模量和面内等效模量。相比于面内等效模量，面外等效模量远大于面内等效模量，因此可得，蜂窝芯层结构面外抗载荷能力大于蜂窝芯层面内抗载荷能力。为深入研究芯体结构功能应用，建立蜂窝芯体的面外等效模量模型是必要的。根据胞元理论将弧形类蜂窝芯层结构进行简化，得到基本单元体（如图3所示），为了有效研究弧形类蜂窝结构，取2为π/4。在基本单元体上施加纵向载荷（如图4所示）。可推导单元体的蜂窝壁应变为：

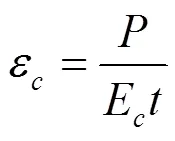
式中：σ为基本单元体上的应力，GPa；ε为基本单元体的应变；为蜂窝壁单位长度上承载的载荷，N；为基本单元体胞壁厚度，mm；E为弧形类蜂窝基本单元体材料的弹性模量，GPa。

弧形类蜂窝蜂窝芯体单元体承受的总载荷为：

式中：为常数，＝90°，为四个边长长度，mm；为四个弧形外径，mm；为四个弧形内径，mm；1为四个弧长的的圆心角，rad。

将基本单元体等效为均质体，即基本单元体等效为具有均匀性、连续性的面板。则可推导出，在基本单元体总载荷作用下，均质体的应变为：

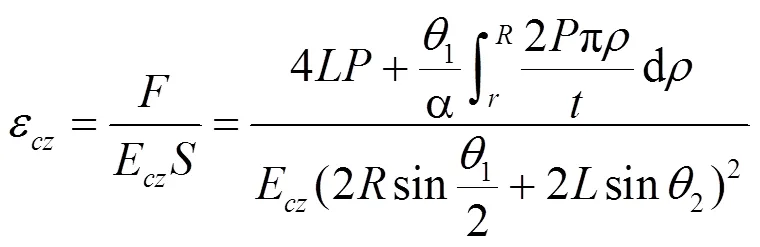
式中：εcz为均质体的应变；S为均质体的面积，mm2；Fcz为均质体的弹性模量，GPa；F为均质体上的总载荷，N。

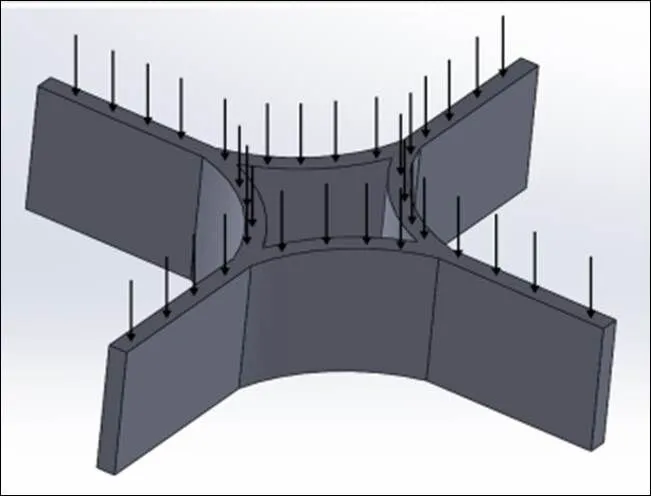
图4 单壁厚芯体的基本单元体面外纵向载荷

根据前文所述，基本单元体等效为均质体，两者的应变相等，因此可得：

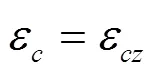
故可推导得：

2.2 等壁厚弧形类蜂窝夹芯结构面外等效剪切模量

当弧形类蜂窝夹芯受到面外剪切力时，剪切力τ以剪流的形式在基本单元体胞壁上进行传递。假定单元体胞壁上剪切力的作用方向为轴，面外剪切力分布均匀，可推导基本单元体的方向上的总载荷为：

如图5所示，由于单元体关于、轴对称，在剪切力的作用下，蜂窝壁单位体积的应变能为：

式中：uc为单元体的单位体积应变能，J/mm3；Gc为基本单元体材料的剪切模量，GPa。

可推导出基本单元体的应变能为：

式中：为常数，＝180°；U为基本单元体的应变，J；v为基本单元体体积，mm3；h为基本单元体的高度，mm。

根据上文所述，基本单元体承受面外剪切力与面板上的作用力相等，即Q＝Q，通过已知的条件，可推导出，在横向剪切力的作用下，均质体的应变为：

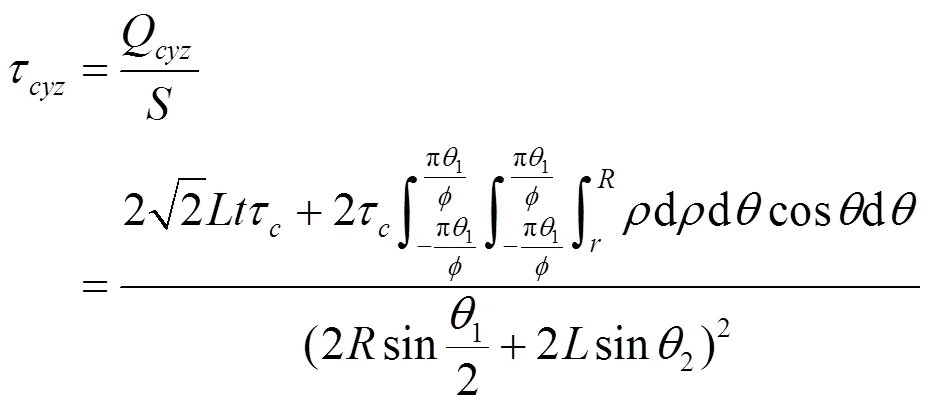
式中：τ为均质体上的剪切力，GPa；Q为均质体上的总剪切力，N。

则均质体在横向剪切力的作用下，应变能为：

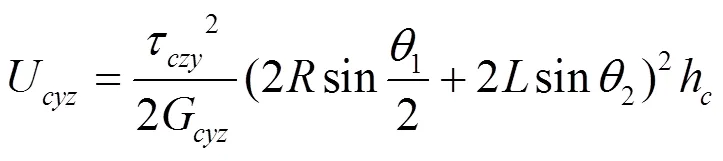
式中：U为均质体上的应变能，J；G为均质体的剪切模量，GPa；τ为均质体上的切应力，GPa。

根据前文可得U＝U，结合述式（9）和式（11），可得均质体的等效剪切模量为：

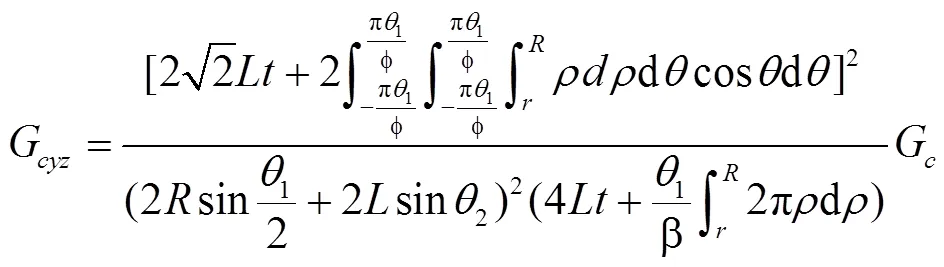
3 算例分析与对比

通过已推导理论公式，研究同等密度下，弧形类蜂窝芯体与传统蜂窝芯体力学性能，需要推导出两者基本单元体的密度。根据前文，可得基本单元体的体积为：

基本单元体的质量为：

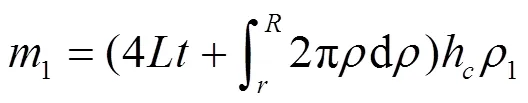
基本单元体等效模型的体积为：

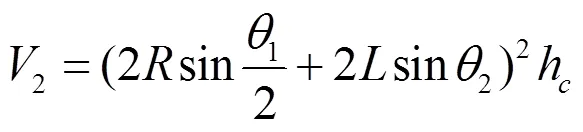
基本单元体等效模型的质量为：

式中：2为基本单元体等效模型材料的密度，g/mm3。

根据等效前后质量守恒原理，可得1＝2，因此可得：

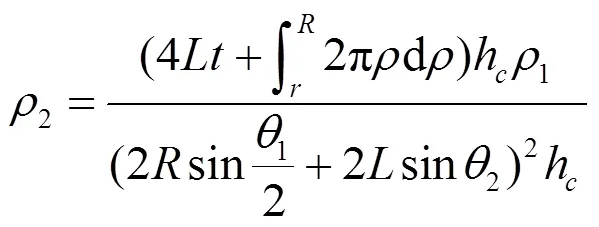
取1＝60°、2＝45°、＝，可将式（12）简化为：

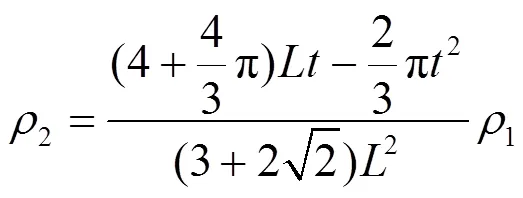
将具体数据代入公式，经过推导可得，在相同的密度条件下，弧形类蜂窝芯层面外剪切模量有显著的提高，对于抵抗受外剪切力，弧形类蜂窝芯层结构具有更优良的性能。

4 双壁厚弧形类蜂窝芯层等效模量

4.1 双壁厚弧形类蜂窝芯层等效弹性模量

传统的蜂窝芯层主要以等壁厚与双壁厚两种不同的结构应用于工程。为了推进应用进程，推导双壁厚弧形类蜂窝芯层等效弹性模量。该结构单胞如图6所示，简化结构，可得基本单元体如图7所示。施加轴方向载荷，如图8所示，由此可得双壁厚弧形类蜂窝芯层总载荷为：

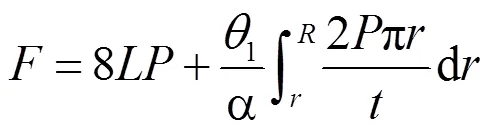
弧形类蜂窝芯层基本单元体材料的弹性模量为E，可推导出弧形类蜂窝芯层基本单元体的应变为：

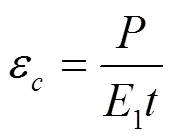
图6 双壁厚弧形类蜂窝芯层单胞尺寸参数

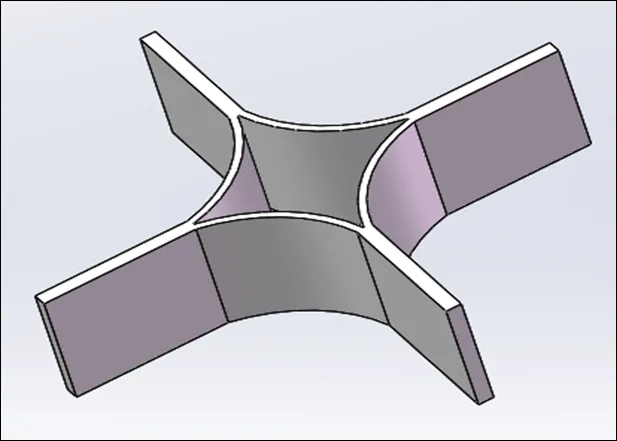
图7 单壁厚芯体的基本单元体

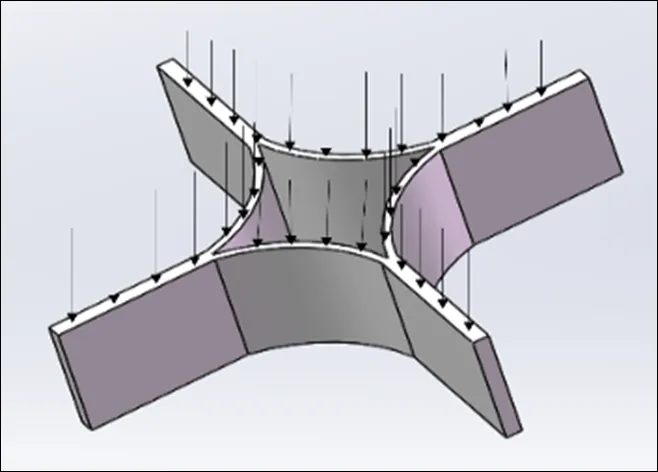
图8 单壁厚芯体的基本单元体面外纵向载荷

均质体的应变为：

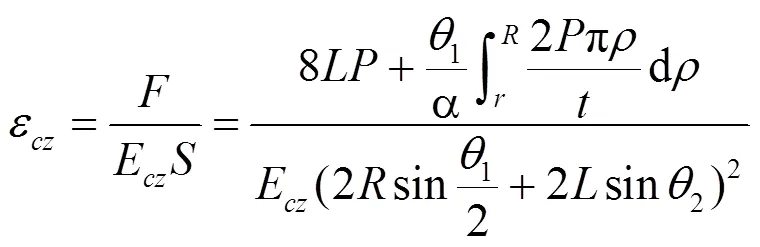
由于基本单元体与均质体的应变相等，即ε＝ε，结合以上公式，可得双壁厚新型蜂窝芯层等效弹性模量为：

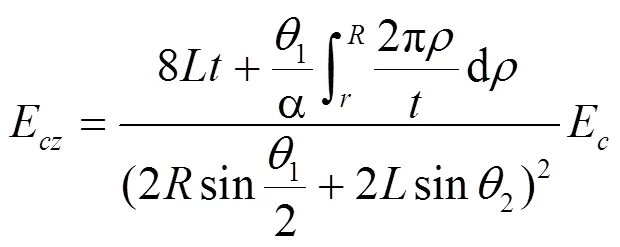
4.2 双壁厚弧形类蜂窝芯层等效剪切模量

对于双壁厚弧形类蜂窝芯层等效剪切模量的推导，由于弧形类蜂窝芯层关于、轴对称，可得其剪流的情况，如图9所示，当轴受力时，双壁厚弧形类蜂窝芯层受到的总载荷为：

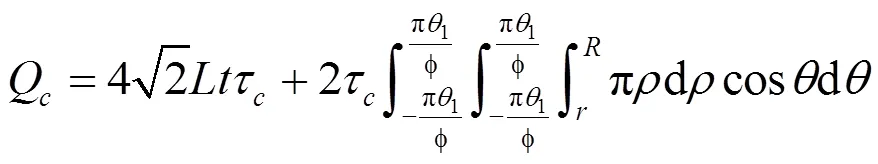
基本单元体的单位体积应变能为：

基本单元体的应变能为：

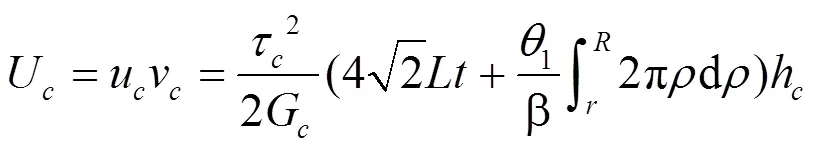
均质体在横向剪切力的作用下应变能为：

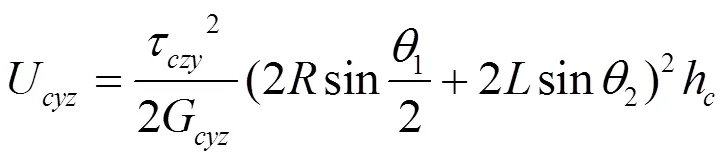
由于基本单元体与等效均质体的应变能相等，即U＝U，结合以上公式，可得双壁厚弧形类蜂窝芯层等效剪切模量为：

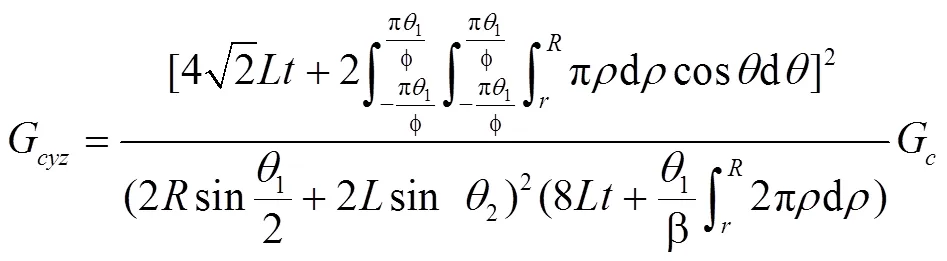
5 仿真验证

采用ABAQUS软件对该结构面外等效模量理论公式进行验证，上下面板、蜂窝芯层均采用solid实体单元，弧形类蜂窝芯层的材料参数为：密度＝2.78×1012g/m3，弹性模量＝71 GPa，泊松比＝0.33。将上下面板表面与芯层上下表面绑定，对上刚性面板施加、方向作用力均为0.1 MPa，＝0.3 mm，＝＝6 mm，1＝60°，2＝45°。

通过ABAQUS对弧形类蜂窝芯层面外等效模量进行数值计算，如图10、图11所示，可得其在仿真计算下的面外等效模量。

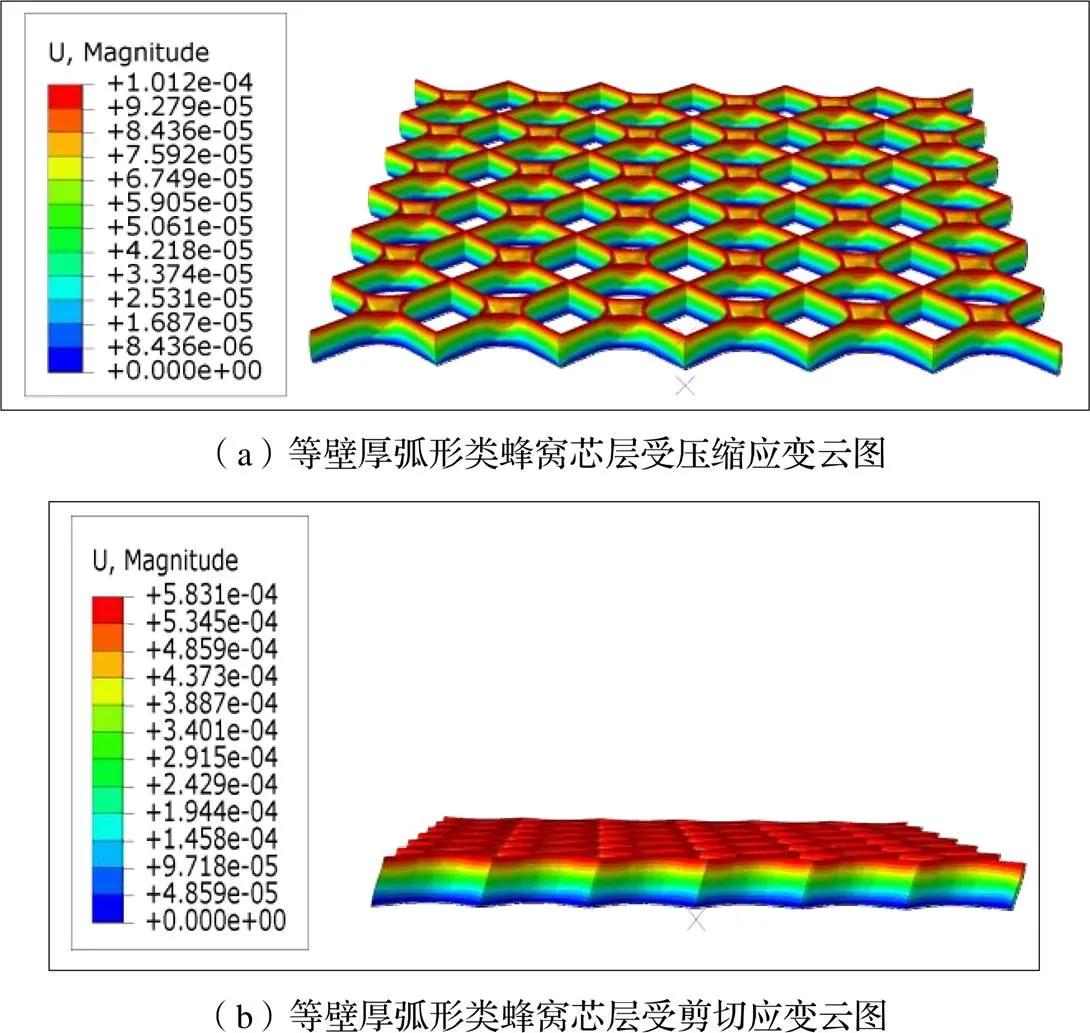
图10 等壁厚弧形类蜂窝芯层应变云图

图11 双壁厚弧形类蜂窝芯层应变云图

仿真值与理论值之间的相对误差在10%以内，如表1和表2所示。从而可得，弧形类蜂窝芯层面外等效力学模量的理论公式具有可靠性，可作为工程应用的理论依据。同时，将双壁厚蜂窝芯层结构与单壁厚蜂窝芯层结构进行对比，发现双壁厚蜂窝芯层结构承载能力有显著的提升。

表1 等壁厚新型蜂窝芯层结构的相对误差

表2 双壁厚新型蜂窝芯层结构的相对误差

6 结论

（1）由于蜂窝芯层结构在实际应用中存在等壁厚夹芯结构与双壁厚夹芯结构，笔者使用经典胞元理论及材料力学的知识对两种不同壁厚新型蜂窝芯层结构面外等效模量进行推导；

（2）通过阅读国内外研究学者对传统蜂窝芯层结构的研究成果文献，获得传统蜂窝芯层结构面外等效模量公式，在相同密度下，对比两者的面外剪切模量，可得到弧形类蜂窝芯体面外抗剪切能力大于传统蜂窝芯体，可用于剪切力较大的特殊工况；

（3）运用有限元商业软件ABAQUS，对比弧形类蜂窝芯层结构的面外等效模量公式，理论值与仿真值之间的误差在10%以内，从而可得，经过经典胞元理论及材料力学知识对两种不同壁厚新型蜂窝芯层结构面外等效模量表达解析式具有准确性，可应用于实际工程。

[1]Del Broccolo S，Laurenzi S，Scarpa F. AUXHEX-A Kirigami inspired zero Poisson’s ratio cellular structure[J]. Composite Structures，2017，176：433-441.

[2]Grima J N，Oliveri L，Attard D，et al. Hexagonal honeycombs with zero Poisson's ratios and enhanced stiffness[J]. Advanced Engineering Materials，2010，12（9）：855-862.

[3]王玮. 零泊松比蜂窝结构的设计及应用[D].大连：大连理工大学，2019.

[4]蒋伟，马华，王军，等. 基于环形蜂窝芯结构的负泊松比机械超材料[J]. 科学通报，2016，61（13）：1421-1427.

[5]沈建邦，肖俊华. 负泊松比可变弧角曲边内凹蜂窝结构的力学性能[J]. 中国机械工程，2019，30（17）：2135-2141.

[6]李响，周幼辉，童冠，等. 超轻多孔类蜂窝夹心结构创新构型及其力学性能[J]. 西安交通大学学报，2014，48（9）：88-94.

[7]陈永清，仇琨，李响. 类蜂窝夹层结构振动特性分析及应用研究[J]. 机械，2022，49（1）：9-15，36.

[8]李响，潘志宇，李锐，等. 轻质高强类蜂窝夹层结构力学性能分析及优化[J]. 机械，2021，48（11）：1-9.

[9]周星驰，唐振刚，周徐斌，等. CFRP圆形胞元蜂窝芯层面外剪切模量[J]. 复合材料学报，2018，35（10）：2777-2785.

[10]吴建均，王永静，谢敬尧，等. 泡沫波纹复合夹心梁等效弹性常数的推导及其振动特性研究[J]. 西安交通大学学报，2018，52（11）：73-80.

[11]Kelsey S，Gellatly R A，Clark B W. The shear modulus of foil honeycomb cores：A theoretical and experimental investigation on cores used in sandwich construction[J]. Aircraft Engineering and Aerospace Technology，1958，10（11）：294-301.

[12]Gibson L J，Ashby M F，Schajer G S，et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences，1982，382（1782）：25-42.

[13]赵剑，谢宗蕻，安学峰，等. 蜂窝芯体材料面外等效弹性模量预测与分析[J]. 航空材料学报，2008（4）：94-100.

[14]富明慧，徐欧腾. 关于蜂窝芯体面外等效剪切模量的讨论[J]. 固体力学学报，2014，35（4）：334-340.

[15]王梁，刘海涛. X型内凹蜂窝结构的拉伸力学行为研究[J]. 机械强度，2020，42（4）：896-900.

[16]齐佳旗，段玥晨，铁瑛，等. 结构参数对CFRP蒙皮－铝蜂窝夹层板低速冲击性能的影响[J]. 复合材料学报，2020，37（6）：1352-1363.

Equivalent Mechanical Properties Outside the Layer of Arc-shaped Honeycomb Core

YIN Shengdi1，TANG Shuangqing1，LI Xiang1,2，QIU Kun1，DUAN Yu1，CHEN Tao1

( 1.College of Mechanical and Power Engineering, China Three Gorges University, Yichang443002, China; 2.Hubei Engineering Research Center for Graphite Additive Manufacturing Technology and Equipment (China Three Gorges University), Yichang 443002, China )

In order to improve the out-of-plane bearing capacity of the honeycomb structure, an arc-shaped honeycomb-like sandwich structure was proposed from the perspective of innovative design, and its out-of-plane mechanical properties were studied. Firstly, the arc-shaped honeycomb-like sandwich structure is simplified by using the cell theory, and the analytical expression of its out-of-plane equivalent modulus is deduced by using the knowledge of material mechanics and the energy methods. Then, the arc-shaped honeycomb-like core layer structure is compared with the traditional honeycomb-like core layer structure. Under the same equivalent density, it is found that the out-of-plane shear modulus of the arc-shaped honeycomb-like core layer is significantly improved through specific data verification. At the same time, the out-of-plane equivalent modulus expression of the double-wall-thickness arc-like honeycomb is derived. Finally, using numerical simulation analysis, the simulation value of the structure is obtained. After comparing the theoretical value and the simulation value, it is found that the relative error between the two is within 10%, which proves the accuracy of the derived theoretical formula of the out-of-plane equivalent modulus.

arc-shaped honeycomb sandwich；out-of-plane equivalent mechanical model；energy method；numerical simulation

O342

A

10.3969/j.issn.1006-0316.2022.11.001

1006-0316 (2022) 11-0001-08

2022-02-28

国家自然科学基金青年科学基金（51305232）

殷圣地（1997－），男，湖北黄梅人，硕士研究生，主要研究方向为轻量化技术，Email：1572429532@qq.com。*通讯作者：李响（1979－），男，湖北黄梅人，博士，副教授，主要研究方向为轻量化技术、结构优化设计、数值模拟技术、结构强度与可靠性等，Email：lixiangcfy@ctgu.edu.cn。