从数学模型向力学模型的极小曲面薄壳的数字建构*

苏朝浩 张枢健 何永鹏 陈庆军

(1.华南理工大学建筑学院， 广州 510630； 2.华南理工大学建筑设计研究院有限公司， 广州 510630；3.亚热带建筑科学国家重点实验室， 广州 510630； 4.巴斯大学建筑与土木工程系， 巴斯 BA2 7AY；5.华南理工大学土木与交通学院， 广州 510630)

0 引 言

在日益普及的建筑数字化设计语境下，形式的自由与力学法则之间的偏差始终存在且难以避免。如何在两者之间建构起新的平衡态以取得形式自由与客观约束的统一，构成了国际范围内一个热点的交叉学科研究课题。“参数化主义者” Patrik Schumacher[1-2]一直在思考着这个问题，他“越来越多地尝试从自由构造复曲面转向寻求结构找形的算法”[3]；其他学者也在探索以计算机与结构有限元分析理论为技术手段的结构性能生形的研究方向，旨在创造高性能、高适应性和动态性的结构系统[4]。

作为建筑的结构——将结构的内在力学逻辑以建筑语言的形式表达，是现代建筑的一个重要分支[5]。自2012年开始，国内每年一届的“建筑、结构巅峰对话：结构成就建筑之美”学术会议成为年度盛事。在国内设计业界，学者和设计师们经常就如何将数字化设计推向实用、形态复杂性与结构性能如何协同等问题展开了热烈的讨论。这其中结构题材、结构潜能以及结构艺术[6]正在成为日益关注的话题。

将非规则曲面中的一种特殊类型“极小曲面”[7]作为研究对象，是基于以下几个方面因素的考虑：第一，极小曲面具有典型性。它具有外观复杂而多变的混沌状态，由一系列的正、反高斯面组成，其实质是由数学方程式控制、蕴含着的一种内在秩序。第二，它展示了特殊而新颖的空间形式动力和艺术状态。一个毫无内、外边界可言的“虫洞”弥漫着神秘的混沌空间魅力，同时呈现着一种内在的逻辑美感——数学之美[8]。第三，它极度轻薄，趋同于高性能的薄壁结构形式，存在高难度的制造技术挑战性。

复杂的形与内在的力，如何建立起有效的协同关系，构成了问题的本质：力与形的关系分析及建构[9]。因此，将结合一个实验性的异规薄壳体案例——《云间玲珑》[10](图1、2)，重点从力与形的关系分析、力与形的关系建构两方面阐述数学模型向力学模型转化的探索过程。此极薄结构的板厚度仅为1.5 mm，约为球体直径的1/5 000。目前关于极薄空间结构的设计思路文献很少，如何实现合理、安全的构型是研究的关键。

图1 极小曲面作品——《云间玲珑》在2019—2020广州国际灯光节上展出Fig.1 A minimal surface work Yunjian Linglong on display at Guangzhou International Lighting Festival in 2019-2020

图2 极小曲面作品——《云间玲珑》呈现的轻薄结构艺术与混沌美学形态Fig.2 The light and thin structure art and chaotic aesthetic form presented by the work minimal surface Yunjian Linglong

1 力与形的关系分析

1.1 异规空间抵抗作用

空间结构的概念或定义虽然因人而异，然而基本特性主要包括两点：形态抵抗和空间抵抗[11]。空间抵抗来自于立体构件布置所带来的空间的结构抵抗。单个悬索、拱利用了拉、压力进行力的传递，但索膜结构、穹顶结构等空间抵抗作用是与单个拱、悬索等形态抵抗完全不同性质的性能转变。虽然结构形态包括了几何形态，然而实质上是“力学上的形态”，即由平衡形状与力流、或者由形态抵抗而联想到的“形与力的结合形态”。因此，要认识和利用结构形态，关键是如何认识和梳理力与形的关系模式[12]。很明显，单纯的拱、索结构原型，已不适应带有正、反曲率高斯面的极小曲面模型。在空间上互相拉结的曲面单元，更倾向于形成异规的空间框架体系。该异规空间体系，有别于笛卡尔正交坐标下的梁-柱结构体系，各个单元是通过空间不同方向的互相约束作用而产生整体空间刚度。因此，适应于极小曲面的结构构型，并非来自平面体系的形态抵抗作用，而是源自三维的空间抵抗作用，是力与形关系在空间抵抗上的异规建构。

1.2 从均质向集聚的层次化秩序转化

形象地讲，极小曲面呈现的肥皂泡沫和海绵体的形态特征具有均质性。但对于扭曲、轻薄的异规曲面而言，这种均质性对于形成整体空间刚度和传力路径却非常不利。而且由于极度轻薄，导致单元体面外刚度缺失，压力状态下局部容易失稳。由均质向集聚进行变形，以形成力流的层次化传递路径，是一个重要的思路。通过集聚以进行刚度的重新分配，可形成树状结构层次，主干和枝丫各自分工；另外，集聚对于增加单元的面外刚度也起到了积极作用，从而提升结构强度和稳定性。

1.3 数学模型向力学模型的变形转化

极小曲面由数学算法生成，是纯粹的几何模型，而不是一个物理环境中的力学模型。在力学工况下，纯几何模型需要向力学模型进行变形和转化。因此，生成极小曲面的算法中需考虑这种转化的可能性和可操作性，使得极小曲面单元处于一个动态可调度的状态，并按照一定的力学建构规则进行变形和重构，适应反复调控、评估、优化的过程需求，最终达成力与形的关系统一。

2 力与形的关系建构

2.1 由均质泡沫向整体空间管状框架转化

基于异规空间抵抗作用、从均质向集聚的层次转化思想，力与形的关系建构，可以从基本形的生形算法切入，调适和优化算法，将均质泡沫向管状体进行集聚，形成树状结构的主干层次和传力路径，同时通过结构计算进行性能验证。

2.1.1基本算法

采用由Panagiotis Michalatos研发的Millipede插件工具进行生形[13](软件平台为Rhino及插件Grasshopper)。它的生成逻辑是：首先，在一个空间范围内，布满很多的点，然后根据表达式计算出的这些点的值，判断这些值是否大于零，并将点分成大于零和不小于零两个部分；第二，确认以上两个部分中相互离得比较近的点，即是零附近的点，然后将这些点取出来，将它们联合成面；最后，便是用一个方形拼接来近似描述目标曲面，再将网格划分后的面进行平滑处理，即可得到目标曲面。在生形程序中通过调用不同的数学方程，可生成不同种类的“泡沫”单元(图3、4)。图3中，在数学领域中，极小曲面由数学算法生成。极小曲面是平均曲率等于零的曲面，即是满足特定约束的条件，达到稳定的表面积最小的曲面。

a—f(x,y,z)=zcos x-cos y; b—f(x,y,z)=cos x+cos y+cos z; c—f(x,y,z)=sin xsin ysin z+sin xcos ycos z+cos xsin ycos z+cos xcos ysin z; d—f(x,y,z)=cos xsin y+cos ysin z+cos zsin x; e—f(x,y,z)=(4cos xcos y+cos ycos z+cos zcos x-3cos xcos ycos z)/2.4; f—f(x,y,z)=cos xcos y+cos ycos z+cos zcos x-cos xcos ycos z; g—f(x,y,z)=1.1(sin xcos 2xcos ysin z+sin 2ycos zsin x+sin 2zcos xsin y)-0.2(cos 2xcos 2y+cos 2ycos 2z+cos 2zcos 2x)+0.4(cos 2y+cos 2z+cos 2x)。图3 不同函数约束生成的极小曲面形态Fig.3 Minimal surface forms generated by different functional constraints

图4 利用Millipede插件进行极小曲面设计的程序流程Fig.4 The program flow for minimal surfaces designed by Millipede plug-in

2.1.2算法调适形成管状体

通过基本算法得到的泡沫模式较为均质，即使是通过调整计算周期得到不同密度形态，也难以形成理想的力学模型。因此，基本算法须要改进：将空间内的点变成可移动、可操控的点，对这些点进行重新分布(图5)，由均质向集聚模式转化，促使片状单元向管状体逐步转化(图6)，而这些管状体通过正、反曲率的高斯曲面又连成一个整体空间管状框架(图5～7)。此过程中，由于转化程度的不同，会形成形态各异的管状体。

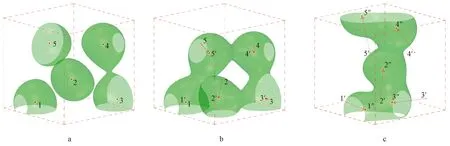
图5 在生形程序中调整控制点以生成管状物Fig.5 Adjusting the control points in the generative procedure to generate pipes

a—随机生成控制点； b—原始状态； c—均质泡沫状态； d—初步形成“管状物”中间状态； e—形成较多“管状物”状态。图6 由均质泡沫状向管状集聚状态转化的过程Fig.6 Processes of transformation from the homogeneous foam state to the tubular agglomeration state

图7 整体空间管状框架模型与3D打印模型Fig.7 The tubular frame model of the overall space and the 3D printing model

2.1.3形态转化的结构性能评估

将上述转化过程的各个状态输入到结构计算软件中进行有限元分析计算。结构分析采用有限元软件ABAQUS软件，用壳单元(SR3)模拟铝片，铝材的密度为2.7 g/mm3, 弹性模量为69 GPa, 泊松比为0.3，施加均布荷载为材料自身重力，边界条件为约束地面接触界面的三个方向的平动自由度。由图8计算结果可得出：

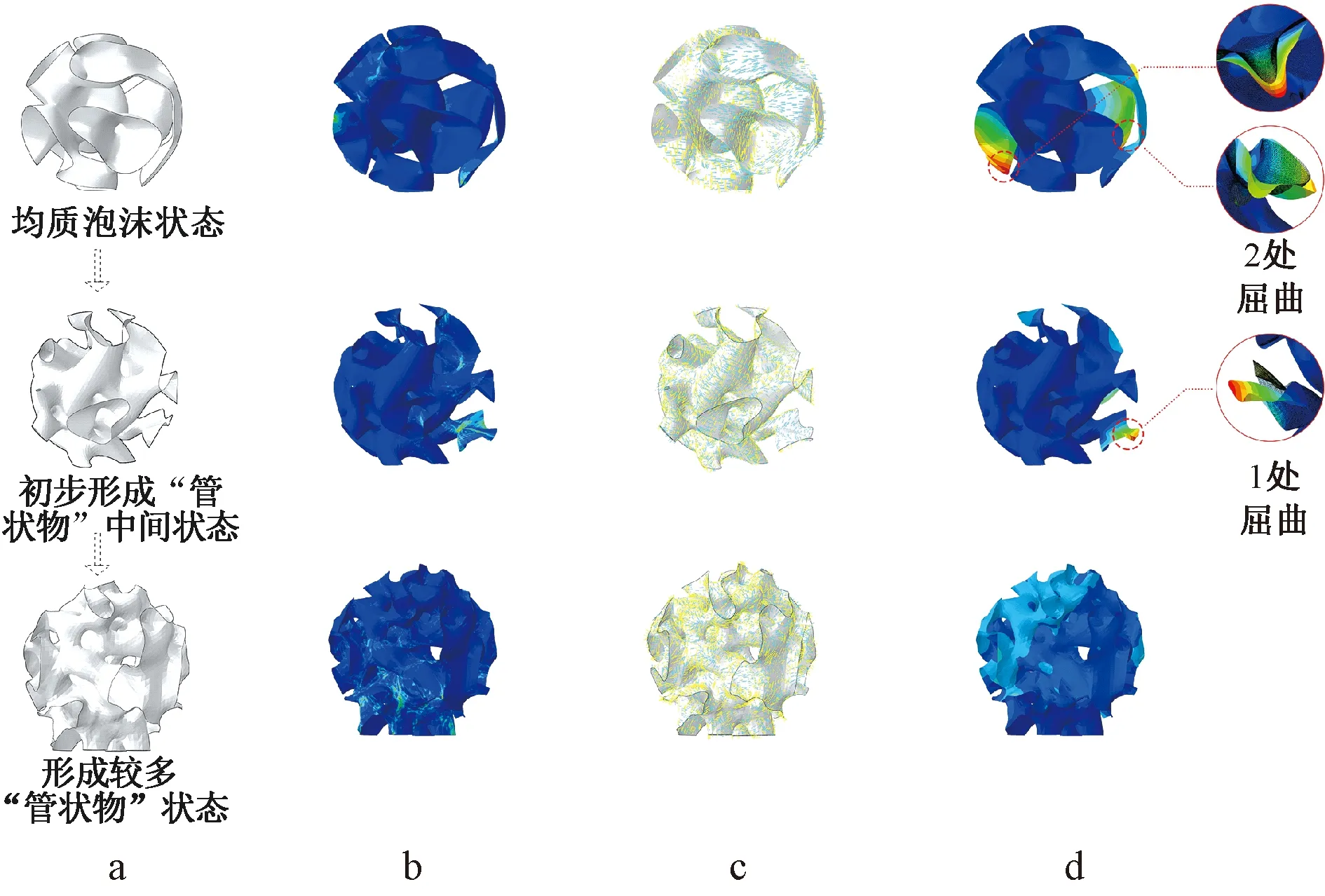
a—状态； b—应力分布； c—应力矢量； d—变形。图8 由均质泡沫状态到管状集聚状态的过程及结构性能验证Fig.8 Processes and structural performance verification from the homogeneous foam state to the tubular agglomeration state

1)由泡沫状向管状物转化的过程，应力集中的现象在逐渐减弱；应力集中的位置由顶部、末端位置转向根部，可见内部大悬挑的状态在逐渐减小；应力的峰值级数由10 MPa减小为0.1 MPa，应力的分布也趋向于更加平均。

2)力流逐渐呈现清晰、便捷的特征，应力矢量图逐渐呈现由枝丫—主干—地面进行传递的树状传力模式。

3)最大位移数值呈现逐渐下降的趋势，由峰值1 246 mm下降为18.8 mm；应力集中的区域数量由2片逐渐减少为零。可见，局部的结构刚度和结构合理性在逐渐得到强化。

2.2 形成环箍效应和构型

轻薄的极小曲面单元，在重力荷载作用下，容易因屈曲而破坏，稳定性差。然而，将这些轻薄的面围成一个桶状体，却能起到柱子的作用。利用环箍效应生成类桶状体，可大大提升薄壁构件的承载力和稳定性。一方面，提取模型中若干组规则状和异规桶状物进行力学计算，虽然不是严格意义上的桶状体，应力分布会受到扭曲的干扰，但是通过观察计算结果可清晰看到环向和竖向上主应力的传递路径(图9)，环箍的作用依然有效。可见，环箍效应概念及原理的引入，对提升薄壁构件的抵抗变形能力和稳定性非常关键。竖向刚度的不足，通过水平环向的约束加以弥补，是一种空间抵抗的力学模式。因此，主干上的极小曲面体，可通过生形程序向桶状体构型进行转化，形成封闭状的形态，让内力从开放式的末梢向封闭状的枝干流动起来，并有效地传递到底部的基础。

图9 各种形状桶状体的环箍效应分析结果Fig.9 Analysis results for the hoop effect of barrels with various shapes

2.3 利用正、反高斯曲率形态的拉结作用

集聚状态下的管状物之间，由一系列具有正、反高斯曲率的面单元进行拉结。力学上，正交方向上的正、反曲率叠加形态跟海帕壳体，也称马鞍面壳体，)的形态特征契合。

2.3.1拱+悬索叠加的力学机制

物理法则上，力总是寻找最有利的形态抵抗路线传递：在两个对角线的方向上形成拱传力与悬索传力叠加机制和空间抵抗作用[14]，当一轴向上受压而产生变形并倾向塌陷时，则在另一轴向上会产生拉应力来阻止此现象的发生。

试验中，对是否添加正、反高斯曲率面单元的两种管状物框架进行结构分析和对比(图10)。位移图表明：添加正、反高斯曲率面单元后的整体刚度得到明显加强，位移值由332 mm减小为158.2 mm；应力矢量图表明:最小主应力和最大主应力的传力路径呈现出清晰的拱+悬索叠加的传力机制。

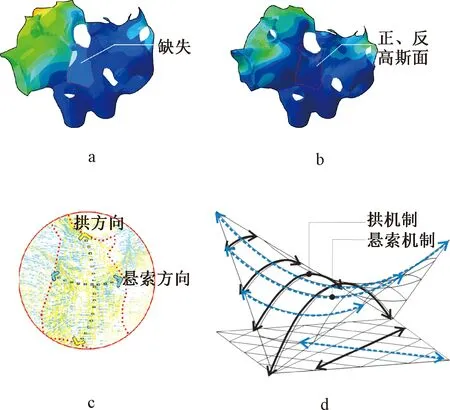
a—缺失正、反高斯曲率面位移； b—添加正、反高斯曲率面位移； c—应力矢量分布； d—海帕壳体力学机制。图10 正、反高斯曲率面单元对管状框架的拉结作用Fig.10 The drawing effect of positive and negative Gaussian curvature surface elements on the tubular frames

为进一步评估这种形态的拉结作用，选了三个模型对其进行力学性能的对比分析。模型分别为B1、B2、B3，模型不同之处在于其与地面接触的管状体分别是1个、2个和3个，并加入了水平荷载进行多工况的力学计算和分析。考虑到该构型的非对称性，在结构分析过程中考虑竖向、水平x及水平y三种方向的荷载工况。荷载施加方式在相应方向上施加指定幅值的加速度。具体如下：

1)工况1：竖向加速度az=-g；2)工况2：水平x方向加速度ax=-g;3)工况3：水平y方向加速度ay=-g;其中，g为重力加速度。

图11～13中给出了模型在重力作用及x向或y向水平作用下的应力云。可以看出：在重力荷载作用下，B3的应力分布比较均匀，结构各部分都较好地参与了受力，最大应力较B1和B2有较大下降。在x向或y向水平荷载作用下，三者的位移值差异不大，拉结形态对于抵抗水平荷载的作用较为明显，表现出良好的结构刚度和稳定性。

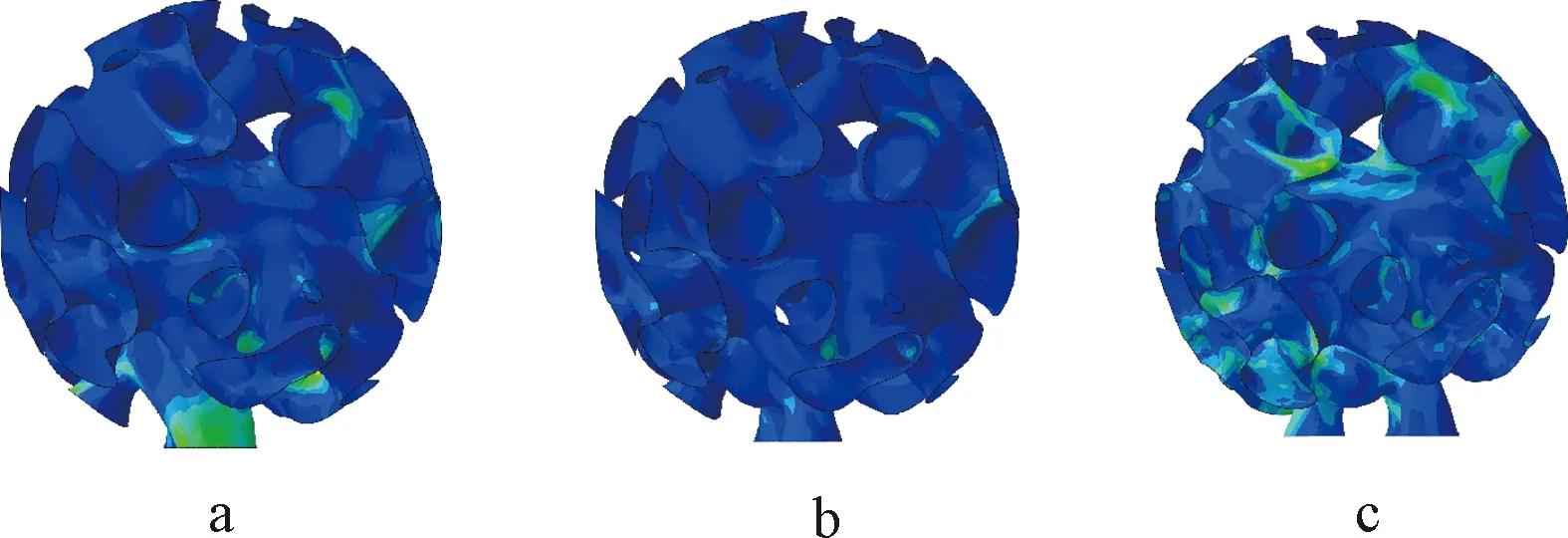
a—B1; b—B2; c—B3。图11 重力荷载作用下应力云Fig.11 Contours of stress under the gravity load

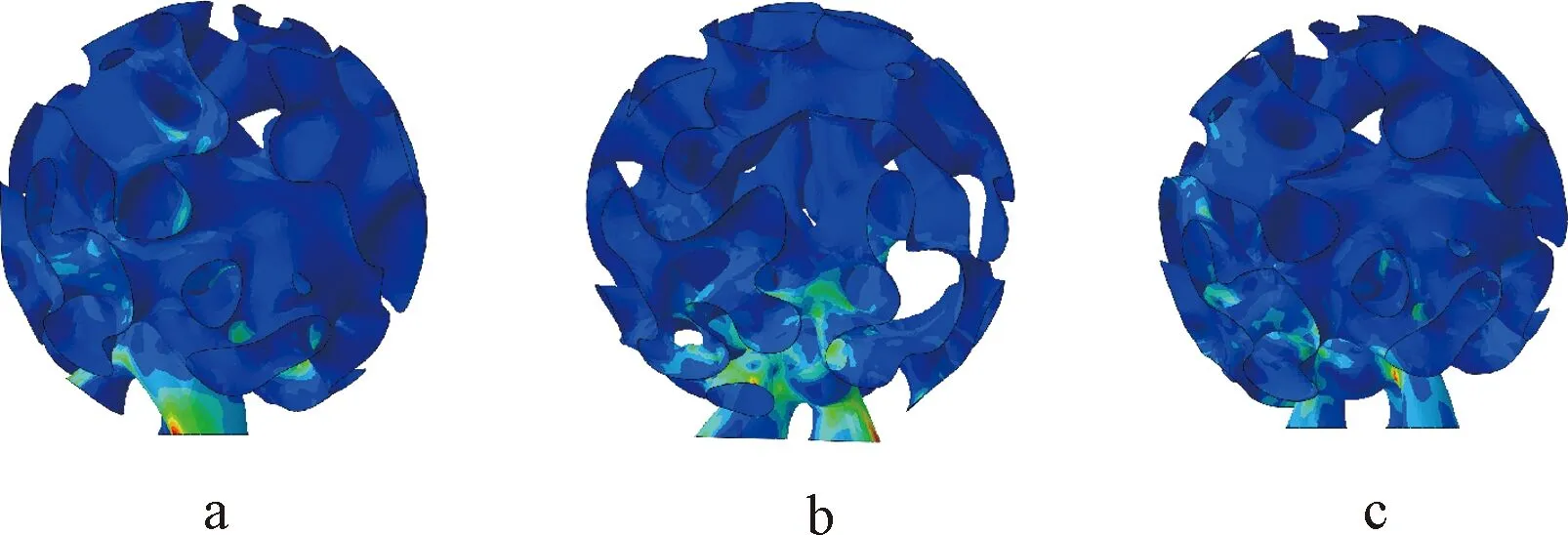
a—B1; b—B2; c—B3。图12 水平向(x向)荷载作用下应力云Fig.12 Contours of stress under the horizontal load(in the x direction)

a—B1; b—B2; c—B3。图13 水平向(y向)荷载作用下应力云Fig.13 Contours of stress under the horizontal load(in the y direction)

2.3.2管状框架与拉结形态间的权衡和空间调度

一方面，管状物通过泡沫状单元之间的拉结作用进行传力和连接成为一个整体；另一方面，整体刚度可在管状物与泡沫单元之间进行调配，从而实现集聚与离散两种空间形态之间的比例分配，实现空间多样性和适应性的调度。

目前如何利用正、反高斯曲率形成管状框架和拉结形态尚未有很好的计算机自动判断算法，只能通过人工完成。

3 制作和建造

数字建构的过程中，形式的“生成”与物质化的“建造”需通过数字技术结合起来[15]。超薄、非规则、大尺度和高度复杂这几个因素，是极小曲面制作和建造方面无法回避的难题和挑战。面向实际应用层面，一种兼顾效率性和经济性的制作方法显得尤为重要。

3.1 “先剖分后组合”的拟合方法

由于异规曲面无法展开为平面，因此，在制作上存在着诸多困难，尤其是对于单元数量庞大的情况，铸模、锻造、捶打等传统的制作工艺已经变得很不经济和适用。

3.1.1拟合原理

首先，将不可展开为平面的异规曲面剖分为有限数量的单元，当单元数量足够大，即趋同于曲面；其次将这些有限数量的单元进行平面化处理(也称拍平)，目的是方便采用计算机数字控制机床进行高效的平面化加工和量化生产；最终，将平面单元进行弯曲拼装以拟合目标曲面。

3.1.2拟合流程

1)网格化和条幅式肋板。将曲面模型进行剖分，网格化为有限数量的三角网格面，根据曲面的曲率大小决定剖分单元数量。条幅式展开即是将具有连续性的相邻三角形网格连接为相互独立的条状单元，便于拍平在一个平面里面进行计算机数字控制机床生产(图14)。

图14 面向计算机数字控制机床技术的极小曲面网格化拆分及平面布置Fig.14 Meshing decomposition and the plan layout for minimal surfaces by CNC techniques

2)链扣式节点设计。将三角形单元外边缘长度进行五等分，并在中间4个分隔点处向外延伸出一定距离的耳板，在耳板范围内预留两个相距16～18 mm的两个圆形孔洞(直径为4 mm)以便铆钉打入。通过链扣式耳板对接构造，一方面在局部产生了刚域和加劲肋，起到了强化面外刚度的作用；另一方面也较为隐秘，达到较好的美观程度。

3)拍平、布置和切割。将带有耳板的条幅式单元进行平面展开，拍平为计算机辅助设计平面图纸进行布置，数控机床便可将布置好的计算机辅助设计图纸进行精准切割和量化生产。

4)拟合目标曲面。这个步骤是将上述已经平面化生产的条幅式平板进行弯折、拼装，拟合出目标曲面。首先，进行相邻三角面交角的标志；第二，根据交角的大小和材料属性进行弯曲和弯折；第三，相邻条幅式单元进行耳板对位，铆钉连接。以此类推，拟合出目标曲面。

3.2 拼 装

对高为7.8 m、直径为7.6 m的大尺度异规曲面模型进行拼装，将面临两个难题：第一，由于非常轻薄(铝板厚度只有1.5 mm，厚度约为球体直径的1/5 000)，整体未成型之前结构刚度低，变形大且容易失稳；第二，单元之间的拼接螺丝孔直径只有4 mm，精准的高空作业是一个巨大的挑战。基于这些问题的考量，最终采用了试装方案如下：先组装管状框架，以产生一定的临时空间刚度，再以管状框架为依托，辅助周边的脚手架进行外围次级结构的组装，最后采用吊车或者龙门架进行高空部分的作业(图15)。

a—激光切割出条幅式肋板； b—肋板按设计角度弯折； c—肋板之间通过铆钉缝合； d—部件组装成型； e—部件组装-低空作用； f—部件排装-高空作用； g—整体组装成型。图15 制作与拼装过程Fig.15 Production and assembly processes

4 结束语

通过数学公式生成的极小曲面，具有特殊的数学美感与空间艺术感染力，可为建筑创作带来新颖而丰富的空间题材。在应对实际应用的复杂性层面，将数学模型向力学模型转化是问题的本质；而力与形的关系分析与数字建构论证，是解决高度复杂异规双曲面壳体现实建造难题的关键所在和有效保证。

极小曲面由数学公式及计算机算法生成，具有特别的数学美感与艺术状态，为建筑空间提供了新颖而丰富的建筑空间创作题材。然而由于其高度形态复杂以及极致轻薄，对结构设计以及曲面制作技术，构成了高难度的挑战。从力学的角度切入，在分析力与形的关系原理基础上，采用定性分析与定量计算相结合的试验方案，重点探讨和论证如何将数学模型向力学模型转换的概念和方法。并基于经济性考量，探讨如何通过参数化设计和计算机数控机床技术的结合，有效地实现对极小曲面进行分解、拟合、制作和拼装。作为一种量化实验的演示和技术路线初探，可为建筑参数化设计与结构力学协同生形的研究提供实证参考与理论线索，可为针对于极小曲面的结构找形的专业软件的面世起积极的催化作用。