短切玄武岩纤维对钢筋混凝土梁抗弯性能的增强效果试验研究*
2022-02-03张津滔
张津滔 刘 茜 郭 瑞,2
(1.西南交通大学土木工程学院, 成都 610031; 2.西南交通大学土木工程材料研究所, 成都 610031)
玄武岩纤维增强混凝土(Basalt Fiber Reinforce Concrete,BFRC)是将玄武岩纤维作为增强材料掺入到混凝土基材中,通过物理力学作用改善混凝土内部结构而不改变混凝土中各种材料本身的化学性能而制成的水泥复合材料[1]。BFRC中增强材料的纤维长度多为30 mm以下,即短切玄武岩纤维增强混凝土。
众多研究证明,玄武岩纤维具有很高的化学稳定性、热稳定性、良好的分散性[2],且与混凝土具有良好的相容性与黏结性[3]。同时,纤维的加入能有效减少混凝土的收缩,增加混凝土的韧性和抗拉强度,抑制裂缝的延展,改善混凝土的最终破坏形态[4-9]。文献[10-14]研究了玄武岩纤维掺量对玄武岩纤维增强无机聚合物水泥混凝土抗断裂指标、强度的影响,发现纤维的加入可以有效改善混凝土的破坏形态,提高混凝土强度,有效抑制裂缝,并提出玄武岩纤维最佳质量掺量为2~2.5 kg/m3(体积掺量约0.7%~0.1%)。此外,针对BFRC梁力学性能研究方面,谭智芳等[15]通过对BFRC梁裂缝试验研究分析纤维掺量、纤维长度对控制试验梁裂缝开展的情况,并得到控制效果随纤维掺量越高、长度越长呈更佳的状态。方圣恩等[16]考虑纤维混凝土梁开裂时极限拉应变与峰值拉应变关系不确定,从塑性变形发展程度系数的角度推导出梁开裂弯矩公式。综上所述,目前有关短切玄武岩纤维长径比对其力学性能的影响尚未得到统一的定论,同时现有纤维混凝土梁开裂和极限特征承载力的计算结果偏于保守,没有考虑纤维对混凝土的增益作用。
因此,本文在总结归纳现有研究的基础上,开展BFRC梁的受弯增强性能试验,通过分析各试验梁的破坏模式,揭示短切玄武岩纤维对混凝土梁抗弯性能的增强作用。同时,基于现有玄武岩纤维混凝土材料力学性能试验数据,建立纤维混凝土抗拉、抗压强度与基体混凝土抗压强度、纤维掺量、纤维长径比之间的关系,并提出BFRC梁开裂和极限承载力预测模型。
1 BFRC梁受弯增强性能试验
1.1 试件设计
本文共设计了1根普通钢筋混凝土梁和3根掺入不同短切玄武岩纤维长度(6 mm、12 mm、18 mm)的BFRC梁。梁试件的截面为b×h=150 mm×200 mm,梁总长为1 900 mm,净跨为1 700 mm,纯弯段长度为500 mm。试件梁的钢筋均采用HRB400,其中受拉侧纵筋布置2根直径16 mm的钢筋,受压钢筋和箍筋的直径为6 mm,箍筋间距为75 mm,混凝土保护层厚度为25 mm。试件的详细尺寸及配筋情况如图1所示。参考CECS 38—2004《纤维混凝土结构技术规程》[17]和文献[10-14],选定纤维较优体积掺量为0.10%。各梁的参数详见表1。

图1 BFRC梁尺寸 mmFig.1 Geometry details of BFRC specimens

表1 试件参数Table 1 Details of specimens
1.2 试件材料
试验水泥采用P·O 42.5;细骨料为河沙,其细度模数为2.9;粗骨料为碎石,粒径范围在5~10 mm之间;水为生活中的自来水。试验混凝土配合比如表2所示。

表2 普通混凝土配合比Table 2 Mix proportion of concrete kg/m3
表3~5给出了试验所用的材料力学性能。其中,混凝土根据GB 50010—2010《混凝土结构设计规范》[18]的要求,每种类型各预留了6个150 mm×150 mm×150 mm的立方体试块,与试验梁在同一室内条件下养护28 d,通过压力机的轴向压缩测试获得试块的平均抗压强度fcu,m和平均抗拉强度ft,m。

表3 玄武岩纤维物理力学性能指标Table 3 Material properties of basalt fiber

表4 钢筋实测材料性能Table 4 Material properties of reinforcement MPa

表5 混凝土和纤维混凝土的材料性能Table 5 Material properties of concrete and BFRC
1.3 试验方法及测点布置
本试验采用四点加载方式。在试件出现竖向弯曲裂缝前,采用的加载速率为5 kN/级;当试件出现弯曲裂缝后,采用的加载为10 kN/级;当试件临近破坏时,将加载速率降为2 kN/级,直至破坏。每级荷载持续时间约为3 min,同时人工手持裂缝观测仪读取每个荷载等级对应的最大裂缝宽度。试验装置如图2所示。
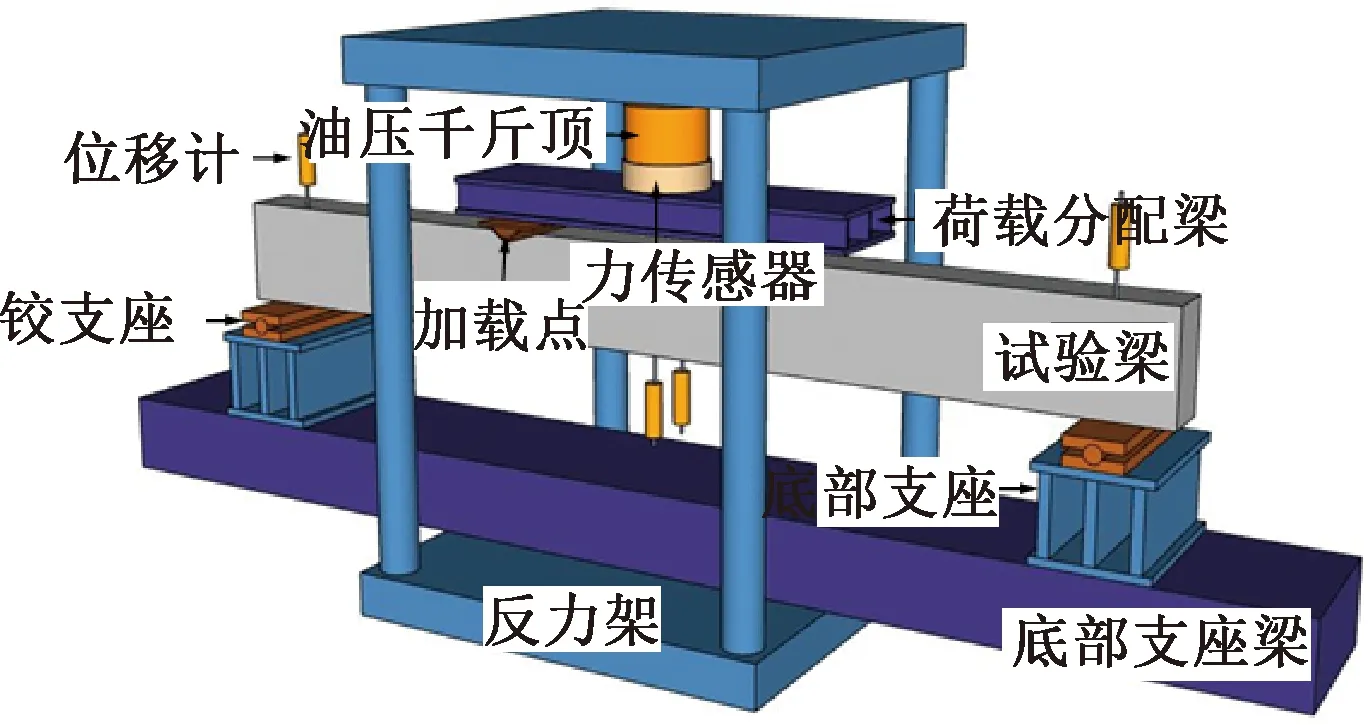
图2 试验装置及仪器布置Fig.2 Test device and its arrangement
应变片和位移计布置情况如图3所示,混凝土应变片用子母“C”表示,C1~C2在跨中底部受拉区,C3~C7分别在高度为50,100,125,150,175 mm的梁侧面,C8~C9在跨中顶部受压区;钢筋应变片用“S”表示,S1~S4均预埋于跨中受拉纵向钢筋表面;位移计分别布置在跨中和两端支座对应位置处。
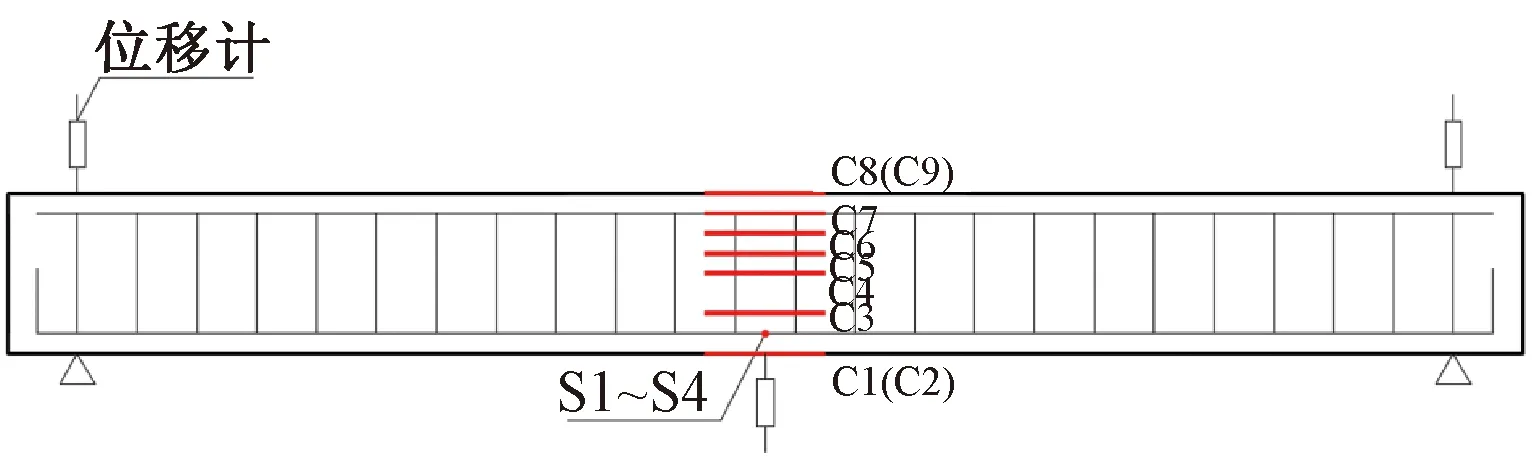
图3 试件测点布置情况Fig.3 Arrangements of measurement points
2 BFRC梁受弯增强效果分析
2.1 破坏模式及裂缝发展
试件的破坏形态如图4所示,BFRC试件与RC试件的破坏形态相似,均呈典型的适筋梁弯曲破坏[1]。RC试件与BFRC试件在受力后构件的裂缝发展和破坏趋势等基本相同,这说明玄武岩纤维的加入对原有RC试件的破坏形态几乎没有影响。

a—RC; b—BFRC6; c—BFRC12; d—BFRC18。图4 各试件裂缝分布Fig.4 Diagrams of concrete crack distribution
在裂缝的条数和发展高度方面,BFRC试件相较于RC试件更能体现玄武岩纤维的抗裂和阻裂作用。RC试件在加载至0.5Py后就几乎不再产生新裂缝,并在达到屈服后裂缝条数一直保持在11条,而BFRC试件加载至1.0Py之前仍会不定的产生新裂缝,并且所有试件裂缝条数最终稳定在13条。裂缝条数的增加使梁跨度范围内的平均裂缝间距减小,同时纤维的掺入有助于抵抗裂缝向高度方向发展。当荷载继续增加接近于Pu时,裂缝数量几乎没有改变,裂缝主要是宽度的发展和高度的延伸。裂缝的分布和发展情况如表6所示。

表6 各试件荷载等级下的裂缝发展情况Table 6 Crack development of specimens under different load levels
2.2 特征承载力及变形性能
如图5所示,四根试件的荷载-挠度曲线均可概括为“三阶段”和“两拐点”,即因竖向弯曲裂缝产生而导致的第一个拐点和因受拉纵筋屈服而导致的第二个拐点将整个荷载-挠度曲线分为了弹性阶段、带裂缝工作阶段和破坏阶段。对比试件可知,在P≈15 kN时,BFRC试件曲线的第一个拐点出现的相对较迟。这意味着玄武岩纤维增大了BFRC试件的开裂荷载,延长了BFRC试件的弹性工作阶段。当P在15~85 kN时,试件处于弹塑性发展阶段,跨中挠度增加,曲线斜率慢慢变小,BFRC试件相对于RC试件在拐点处的转折相对平缓,同时斜率的减小幅度也相对较缓。

图5 荷载-挠度曲线Fig.5 Load-deflection curves of specimens
这主要是因为这些乱向分布的玄武岩纤维在混凝土受拉区承担了部分拉应力,抑制了裂缝宽度发展及长度延伸,使部分本该退出工作的混凝土继续保持受力状态,从而增大了BFRC试件的整体弯曲刚度。当各曲线到达第二个拐点后,即达到了试件的屈服承载力后,荷载的提高幅度非常有限,且挠度会迅速发展直到破坏。各试件的荷载特征值如表7所示。
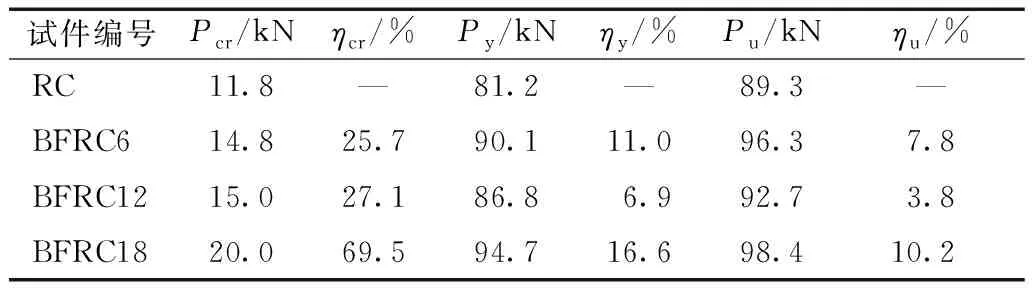
表7 各试件的荷载特征值对比Table 7 Load characteristic values of specimens
从试验中可以发现,短切玄武岩纤维的长度从6 mm、12 mm至18 mm,对应的BFRC试件的开裂承载力提高幅度依次为25.7%、27.1%和69.5%,而其极限承载力相应提高了7.8%、3.8%和10.2%。由此可见,玄武岩纤维的加入对BFRC梁特征承载力有提高作用,并且纤维长度为18 mm的BFRC梁提升最为明显。
此外,可按“最小刚度原则”来计算挠度,见式(1)。通过该式反推在不同荷载等级对应的最小截面弯曲刚度B,并绘制各试件的弯曲刚度-荷载曲线,如图6所示。

图6 弯曲刚度-荷载曲线Fig.6 Relations between bending stiffness and load of specimens
(1)
式中:f为跨中挠度;M为试件的跨中弯矩;l为试件的跨度;S为与荷载形式、支撑条件有关的挠度系数。
由图6可知:1)BFRC试件在正常使用阶段的弯曲刚度较RC试件有不同程度的增大,纤维长径比对刚度的影响明显;2)随着荷载等级的增加,BFRC试件与RC试件的刚度差异逐渐变小,这表明玄武岩纤维的增强阻裂作用主要在构件屈服阶段以前,同时玄武岩纤维的增强作用会随荷载的增加而降低;3)当玄武岩纤维长径比变化时,等体积率掺入纤维长度为6 mm的试件在P/Pu=0.3~0.5范围内的弯曲刚度明显大于其他试件,可能是因为玄武岩纤维分布更均匀且密集,使构件整体的弯曲刚度在加载前期增大的明显。
3 BFRC梁特征承载力预测模型
3.1 既有计算模型
为对BFRC梁的开裂和极限承载力进行预测,提出其特征承载力预测模型,BFRC梁同样满足GB 50010—2010《混凝土结构设计规范》[18]的四个基本假定。其中,以BFRC18为例,随着荷载等级的逐步增加,试件在跨中截面的应变沿高度方向上的变化及其分布大致呈线性变化,基本符合平截面假定,如图7所示。
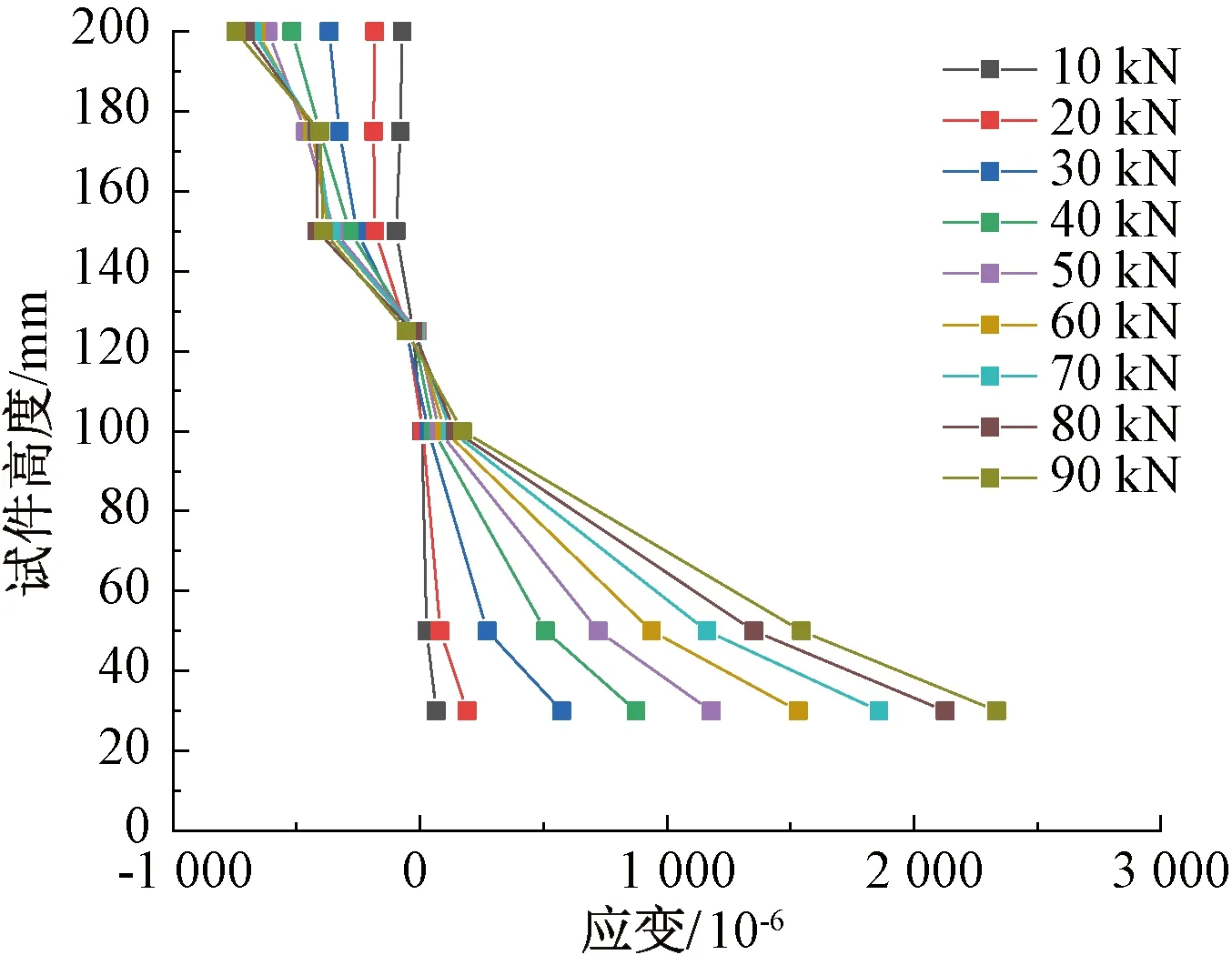
图7 应变沿梁高的分布Fig.7 Distribution of strain along beam height
3.1.2既有公式
在符合平截面假定之下,同时假设混凝土的最大拉应变εt达到轴心受拉峰值应变εt,p的两倍时,混凝土受拉侧边缘开裂,即εt=2εt,p。受压区混凝土应力σc很小,远低于抗压强度fc,故受压区混凝土应力仍呈三角形分布;受拉区混凝土已进入塑性阶段,不是呈线性分布,但因混凝土抗拉强度相较于抗压强度而言很低,故为方便计算,将受拉侧混凝土的应力图简化为梯形分布,同时假设混凝土塑化区高度占受拉区高度的一半,如图8所示。
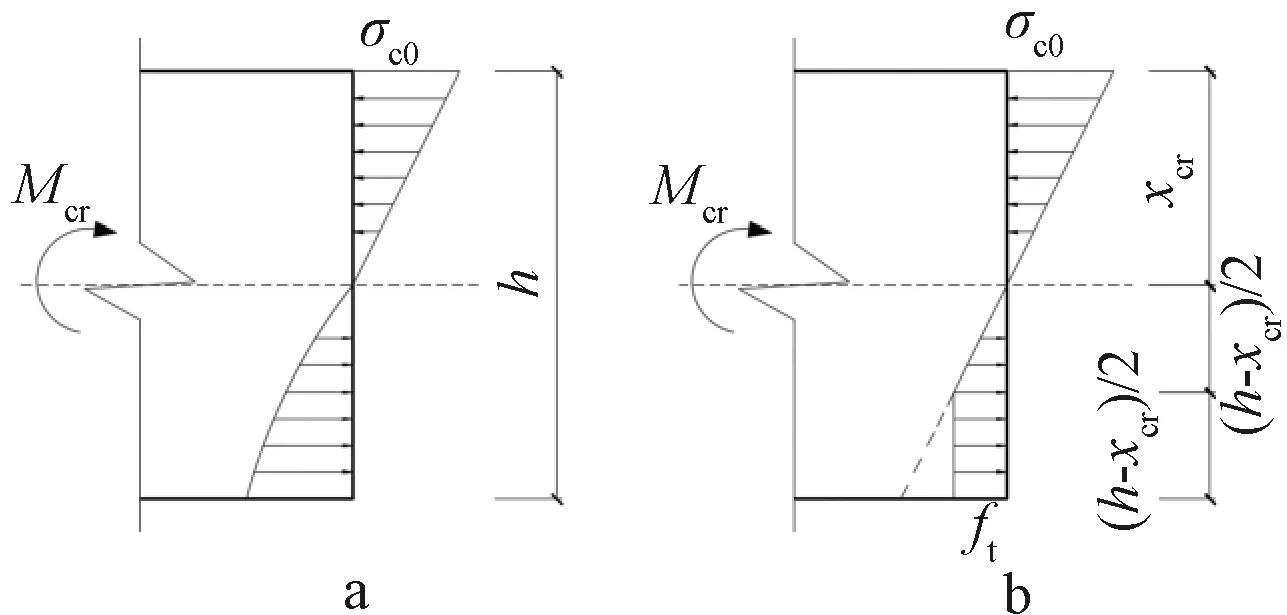
a—实际截面应力; b—计算简图。图8 计算示意Fig.8 Calculation diagram
按照等效换算的方法,即将混凝土梁视为弹性材料,把截面应力图作直线化处理,由此便可得开裂弯矩Mcr:
Mcr=γmftW0
(2)

式中:γm为截面抵抗矩塑性系数;ft为混凝土抗拉强度;W0为受拉边缘的截面抵抗矩,W0=I0/(h-x),其中I0为换算截面惯性矩。
根据BFRC梁受弯试验可知,BFRC梁主要发生了适筋梁的受弯破坏。因此BFRC梁极限状态时纯弯段截面情况如图9所示。其中,从表5和文献[16]中可以看出,普通混凝土和玄武岩纤维混凝土的抗拉强度均小于3 MPa,即混凝土材料的抗拉强度小于其抗压强度的1/10,故假定不考虑纤维混凝土的受拉作用。

a—实际截面应力; b—截面应变。图9 截面受力情况Fig.9 Section stress
由截面力平衡方程可得:
(二)高中班主任应当具备淡泊名利的崇高境界。可以说,一个人的名利观是价值观、世界观以及人生观的具体呈现。树立起正确合理的名利观,便应当不断完善自身的价值观、世界观以及人生观。班主任的辛勤工作绝不是为了追名逐利,而是为了提高学校学生管理的效率及质量。与此同时,作为激励方式,学校也应当授予班主任相应的荣誉奖励,这也是对班主任名利观的考量。观其现状,当前有部分班主任为了一点名利,便将教学质量与教学效率置之不理,与学校领导及同事之间的关系非常紧张,导致班主任整体团队的稳定性也得到了动摇。所以,高中班主任应当具备淡泊名利的崇高境界。
C+T′=T
(3)

T′=σ′sA′s=ε′sEsA′s
T=fyAs
式中:x0为实际混凝土受压区高度;Es为钢筋的弹性模量;ε′s是受压钢筋的应变;fy为钢筋的屈服强度;As、A′s分别为受拉和受压钢筋的截面面积。
由式(3)确定受压区高度x0之后,即可得BFRC梁极限承载力:
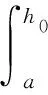
(4)
式中:a为受拉钢筋到中性轴距离;h0为受拉钢筋到梁顶面距离;a′s为受压钢筋到混凝土受压区边缘的距离。
3.1.3计算结果
将BFRC材料性能数据分别代入式(2)与式(4),得到理论开裂承载力和极限承载力计算值,并和试验值进行对比,计算和比对结果见表8。

表8 原特征承载力公式计算值与试验值比较Table 8 Comparison between the calculated values of the original formula and the experimental values
由表8可知,开裂承载力和极限承载力计算值相较于试验值偏小,这是因为在原特征承载力公式中没有考虑玄武岩纤维的增益作用,结果偏于保守,易造成材料的浪费,故需要基于BFRC的基本力学性能,对现有特征承载力公式进行改进。
3.2 改良预测模型
3.2.1纤维混凝土特征力学性能预测模型
纤维混凝土因纤维的存在,其力学性能得到了改变。由既有公式可知,梁开裂承载力和极限承载力分别与混凝土抗拉、抗压强度直接相关。参考CECS 38—2004《纤维混凝土结构技术规程》[17]中钢纤维含量特征值,发现纤维混凝土抗拉、抗压强度与纤维体积掺量、纤维长度、纤维直径、基体混凝土抗压强度有关。定义基体混凝土抗压强度fcu,o,纤维体积掺量为λf,纤维长度与纤维直径的比值为ρ,纤维混凝土抗拉强度ft,纤维混凝土抗压强度fcu。将文献[19-23]试验数据整理如表9所示,并对数据结果进行回归分析,得到纤维混凝土抗拉强度ft,f关于fcu,o、λf、ρ之间的关系式:
(5)
同理,得到纤维混凝土抗压强度fcu,f关于fcu,o、λf、ρ之间的关系式:
fcu,f=fcu,o[1.354 6(1/λf)0.5(1/ρ)0.4+0.832 6]
(6)
分别将按回归分析得到的计算值与试验值做比值处理可以发现,平均值为1.01和1.04,同时离散程度较低,拟合良好,对比结果见表9。
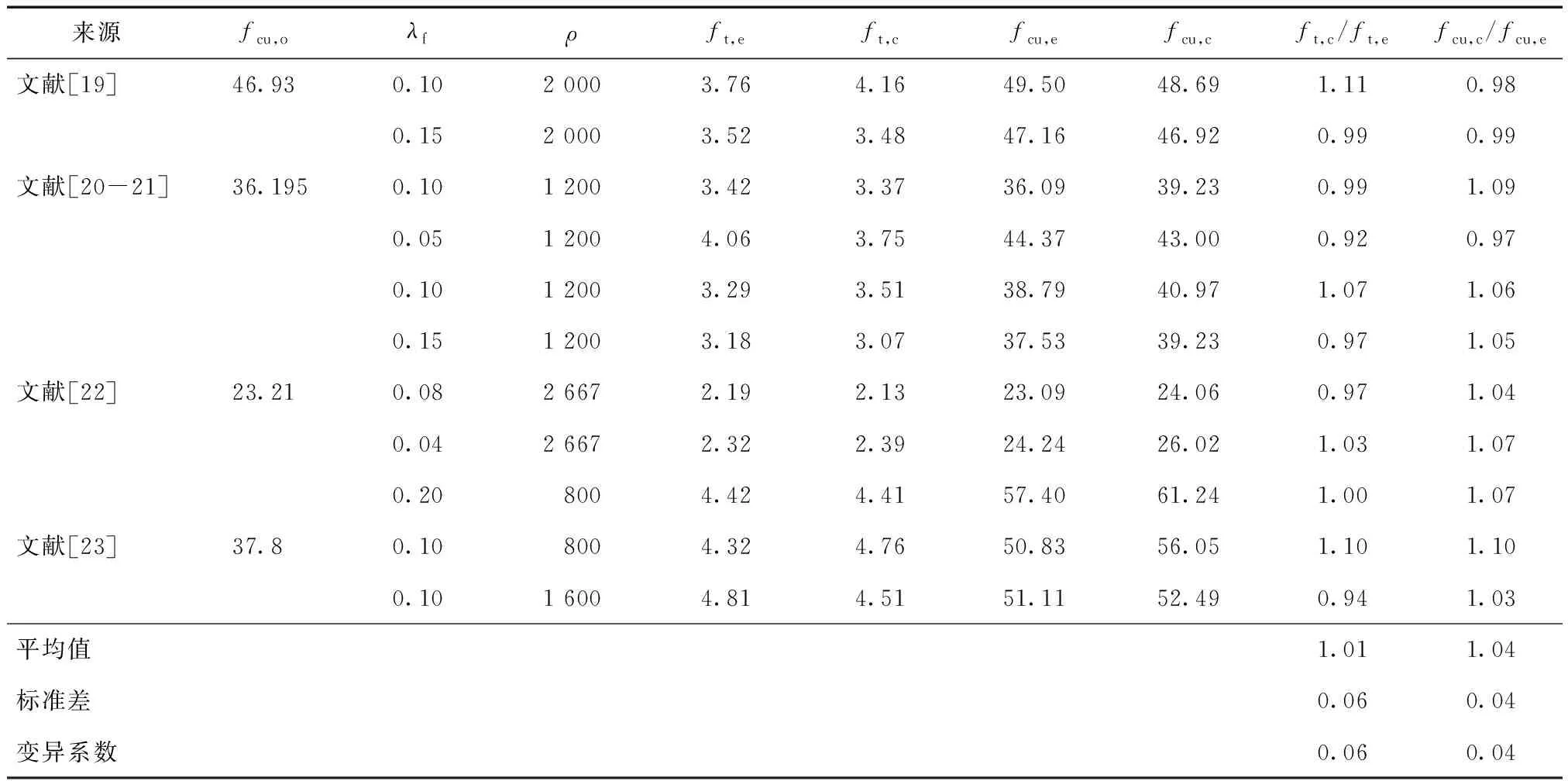
表9 纤维混凝土特征力学性能的试验数据统计Table 9 Test data statistics of characteristic mechanical properties of fiber reinforced concrete
3.2.2改良特征承载力预测模型及验证
以既有的开裂承载力计算模型为改良式理论基础,将改良了的纤维混凝土抗拉预测模型代入,替换原有的混凝土抗拉强度,弥补既有的开裂承载力计算模型中无法有效考虑纤维增益作用的缺陷。同时结合课题组前期研究[24]和相关文献[19-23],取玄武岩纤维混凝土弹性特征系数ν0=0.5,对应应变即为εt=2εt,p。将式(5)代入式(2),即改良开裂承载力预测模型为:
(7)
在极限承载力预测模型中,参照CECS 38—2004[17],当合成纤维体积率不大于0.15%时,合成纤维混凝土的相关系数可以按现行有关混凝土结构设计规范的规定采用,即取正截面的混凝土极限压应变为εcu=0.003 3。再根据截面力平衡与弯矩平衡方程,便可得BFRC梁极限承载力:
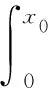
(8a)

(8b)
fc=0.88k1k2fcu,f
(8c)
fcu,f=fcu,o[1.354 6(1/λf)0.5(1/ρ)0.4+0.832 6]
(8d)
式中:k1为混凝土折减系数,取0.76;k2为混凝土脆性系数,取1.00;混凝土轴心抗压强度修正系数取为0.88。
将用改良特征承载力计算式的计算值与BFRC梁的试验值作比对,并结合文献[16,25]的试验数据,数据整理如表10所示。
由表10可知,提出的改良特征承载力预测模型的计算值与试验结果的吻合情况良好,并且离散程度相对较低,能很好反映纤维的在混凝土中的提高作用。对比改良预测模型与原计算式中计算值与试验值的拟合程度,其开裂承载力和极限承载力的比值平均值分别从0.72、0.93升至1.09、0.99,拟合良好。

表10 改良特征承载力公式计算值与试验值比较Table 10 Comparison between the calculated values of the improved formula and the experimental values
4 结 论
1)玄武岩纤维的加入对BFRC梁开裂和极限承载力有提高作用,并且长径比为1 200的BFRC梁的特征承载力提升最明显。
2)适量短切玄武岩纤维的掺入,使混凝土梁在正常使用范围内的最大裂缝宽度减小、裂缝数量增加且裂缝发展延缓,从而提高了BFRC试件的截面弯曲刚度。
3)既有的梁特征承载力计算式中没有考虑纤维的掺入对混凝土性能的增强作用,故计算结果偏于保守,计算式已不再适用。
4)基于相关研究的试验结果得到纤维混凝土抗拉强度和抗压强度计算式,并由此得到BFRC梁特征承载力预测模型,改良预测模型与试验值拟合程度高,适用于纤维混凝土梁的开裂和极限承载力预测。
