基于改进遗传算法的航空器载重平衡

赵向领， 李云飞*， 李鹏飞

(1.中国民航大学空中交通管理学院， 天津 300300； 2.空军某部队， 武汉 430000)

近年来，随着航空运输业的快速发展，这种快速、高效、经济的运输方式深受客户青睐，作为地面保障工作之一的配载平衡工作仍存在着优化空间。为保证飞机在投入运行后能够实现安全且经济的运行，同时便于飞行员轻松操纵，载重平衡工作成为亟待进一步研究优化解决的一个问题。为解决上述问题，现通过建立整数规划模型，使用改进的遗传算法进行求解，以期望使得上述目标能够较好地满足航司要求。

1 问题描述

某些最初设计为客机的飞机可以在必要时改装成多用途飞机来运载货物。特别是近期暴发的疫情更是加快了客机改装进程。飞机所装载的货物类型可以是同类型的也可以是不同类型的。对于航空公司而言，飞机的配载问题是在考虑货物体积和重量约束以及飞机结构约束的情况下，找到飞机上货物的最优装载分布，以实现飞机在运行过程中的平衡，确保飞机安全起飞和降落。

目前航空公司所存在的飞机载重平衡问题的本质是考虑如何合理地分配货物到飞机的舱位，实现飞机重心位置最优和业载量最大。由于问题的复杂度较大，2015年Feng 等[1]在总结当前航空货物运行的文献时指出，飞机的配载问题是航空运输中最基本的多项式非确定性问题(non-deterministic polynomial，NP)-难题组合优化问题之一。近年来在载重平衡问题的求解方法多集中在启发式智能算法和快速发展的商用求解器上。

有关使用启发式智能算法求解载重平衡问题的相关文献有Dahmani 等[2-3]提出的多目标粒子群优化方法，将一组货物分配到最小数量的集装器中，然后将其放置到飞机特定的货舱内，模型考虑了优化业载总重量和优先级；谢春生[4]运用遗传算法建立了民航客机的装载配平模型，并以B747客机为例开发了可视化软件，解决了客机配载员工作强度大、效率低的问题；张洪[5]运用改进的蚁群算法开发了面向C919的配载优化系统；赵向领等[6]建立了民航客改货飞机的载重配平模型，用于解决航空器配载问题，模型以运输业载量最大和重心位置最优为目标，并运用遗传算法进行的求解。谷润平等[7]以货机装载重心最优为目标函数，建立了以重心、重量、结构等约束的混合整数规划模型，依然使用遗传算法求解；史永胜等[8]以货机主货舱为研究对象，建立了重心偏移量最小的目标函数以重心位置、货舱结构、弯矩等为约束条件的整数规划模型，运用遗传算法进行求解；郑琰等[9]研究了货机群装载非标准货物的优化问题，建立了以重心率和空间利用率的目标函数模型，运用启发式算法进行求解；陈璇等[10]采用自适应烟花算法对大型航空运输机装载优化模型求解，装载模型考虑重量、重心、容积、系留等约束条件；孟超[11]针对民航宽体客机腹舱以综合载重利用率和容积利用率最大为目标，运用启发式算法和混和遗传粒子群算法进行求解；白杨[12]分析了客机腹舱和全货机载货两种情况的装载特点，并建立混合整数规划模型，使用基于有效空间的启发式算法求解；朱贺[13]针对货物需要送达同一目的地和货物送到不同目的地，部分货物在中途卸载或者空投的情况，采用了混合整数规划模型分别对这两种问题进行了建模，分别采用了精确求解和元启发求解，并建立相应的软件系统原型。

在使用商业求解载重平衡问题方面的文献有Limbourg等[14]建立的以货物力矩、飞机结构应力和燃油成本最小的混合整数线性规划模型，可以将一组选定的货物分配到飞机的预定位置，并以B747为研究对象使用商业求解器CPLEX验证了模型的有效性；Verstichel等[15]及Vancroonenburg等[16]建立以装载货物价值最大和重心偏移量最小的双目标规划模型，用于解决B747货舱中货物装载平衡的问题，使用Gurobi求解对比了人工配载专家的配载结果，验证了模型的可行性和Gurobi的强大；Lurkin等[17]建立以燃油成本和操作成本最小的混合整数线性模型，考虑了飞机重心约束，用于解决在中间机场取货和交付的飞机装载问题，以B777为研究对象并使用IBM公司的CPLEX进行仿真验证模型；Zhao等[18]把非线性重心包线描述为多段线性约束模型，并设计了线性化策略，在考虑位置、重量、平衡等约束条件下，建立了总业载最大、重心偏差最小的混合整数规划模型。模型使用商业求解器CPLEX可在几秒钟内得到最优解，并且在所有测试实例中保持重心在指定的重心包线范围内；李云飞等[19]使用Lingo求解器验证了客改货飞机的上下舱联合载重平衡模型。

综上所述，国内外对于载重平衡问题通常建立整数规划模型，使用启发式智能算法和商业求解器进行求解。但国内单独对于载重平衡的研究较少，多数是将载重平衡问题作为研究航空货运三维装箱问题一个阶段，考虑的约束不全面，致使模型不完整。另外对于客改货这种新的运输模式的载重平衡的研究还比较少。因此现运用改进的遗传算法研究客改货窄体机的载重平衡问题。

2 载重平衡模型构建

2.1 模型概述

根据目前的主流窄体机选定波音757-200为研究对象，为满足货舱业载量最大和重心偏移量最小的目标，需要建立货舱的配载优化模型。

图1是B757-200的货舱侧视图，可以看出共有15个主货舱、4个下货舱。货机的货舱主要用来装载集装器，下货舱装载散货，此次主要研究主货舱的载重平衡问题。

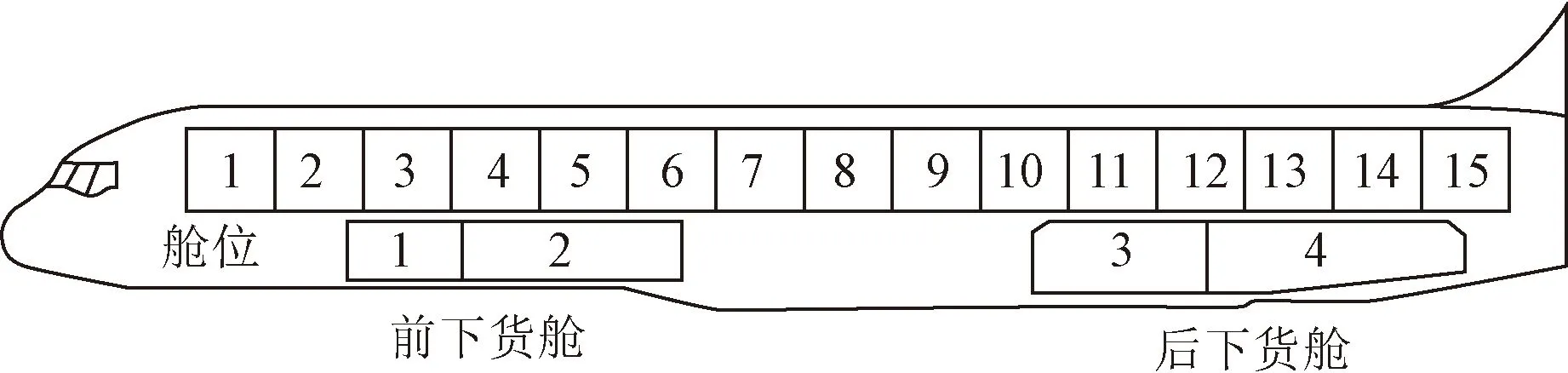
图1 B757-200货机侧视图Fig.1 Side view of B757-200 cargo plane

2.2 目标函数

在模型建立之前首先设决策变量xij为

(1)

式(1)中：i为第i个待装载集装器；j为第j个飞机货舱舱位；NULD为待装载集装器总数；NPOS为飞机主货舱可分配位置的总量。

为保证航空公司运输利润最大化和飞机运行安全，建立了以装载量最大和重心偏移量最小的双目标模型为

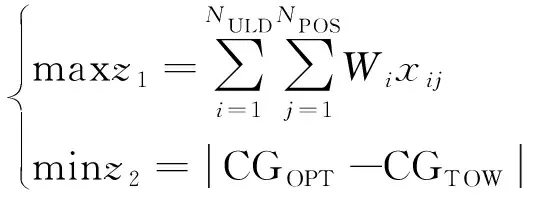
(2)

式(2)中：Wi为第i个待装载集装器的重量；CGOPT和CGTOW分别为飞机起飞最优重心和飞机在起飞重量(takeoff weight,TOW)时的重心，其中CGTOW的计算公式为

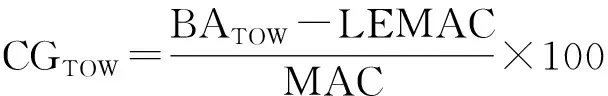
(3)

式(3)中：LEMAC为基准到平均空气动力弦前缘的长度；MAC(mean aerodynamic chord)为平均空气动力弦长；BATOW(balance arm)为起飞重量下的力臂值，计算公式为

(4)

式(4)中：OEW(operation empty weight)为飞机的空机重；BAOEW为飞机的空机重对应的力臂值；TFW(fuel weight)为飞机的起飞燃油重量；BATFW为燃油重量对应的力臂值；BAj为飞机第j个舱位的力臂值。

根据一线配载实际工作情况，现需要将双目标函数冠以不同的权重ω1和ω2，且ω1+ω2=1，与此同时将目标函数做归一化处理，将其转化为单目标函数，即

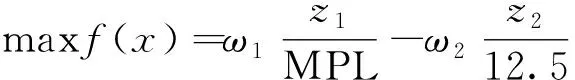
(5)

式(5)中：MPL(max pay load)为飞机的最大业载；12.5为重心包线前后限的一半，以%MAC表示。

2.3 约束条件

在对飞机货舱集装器装载方案进行布局优化时，需要结合实际情况考虑约束，约束条件如下。

(1)保证每个集装器最多放置在一个舱位内。

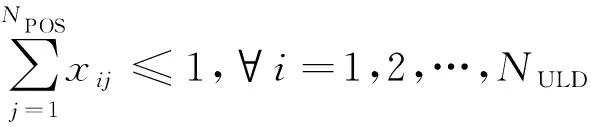
(6)

(2)每个舱位必须保证有一个集装器。

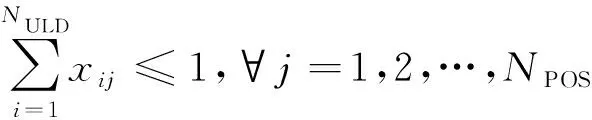
(7)

(3)集装器重量应不超过集装器所在舱位的最大重量。

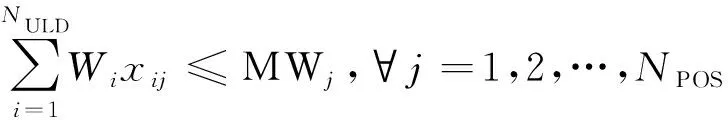
(8)

式(8)中：MWj为飞机第j个舱位的最大载荷。

(4)为保证集装器可以完全装载到货舱内和飞机内壁不受损，货舱内通常会有集装器高度限制，所装载的集装器不能超过所在舱位能容纳的最大高度。

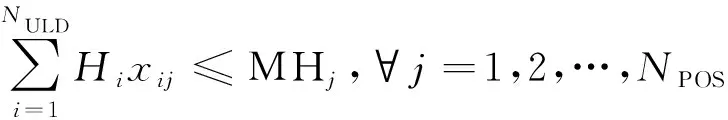
(9)

式(9)中：Hi为第i个待装载集装器的高度；MHj为第j个舱位的最大高度。

(5)飞机的主货舱内一般还存在着分舱位区域限重，主要考虑1～5舱，6～10舱，11～15舱所在区域重量限重。

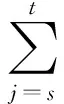
{(s,t)}∈{(1,5),(6,10),(11,15)}

(10)

式(10)中：MWst为主货舱s到t舱的重量限制。

(6)飞机在运行中会受到最大无油重量(max zero fuel weight，MZFW)、最大起飞重量(max takeoff weight，MTOW)、最大着陆重量(max landing weight，MLW)的限制，储备燃料重量(reserve fuel weight，RFW)为飞机的备用油量。

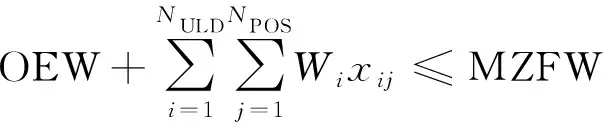
(11)

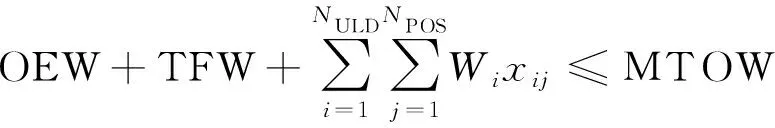
(12)

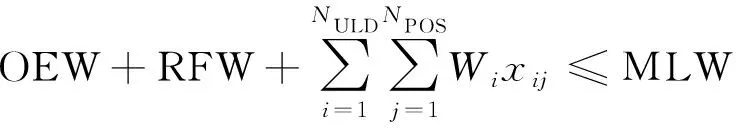
(13)

(7)飞机在运行中还会受到最大业载的限制。

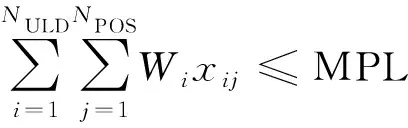
(14)

MPL的计算公式为

MPL=min{MZFW-OEW，MTOW-OEW-

TFW，MLW-OEW-RFW}

(15)

(8)为保证飞机的安全运行，飞机的重心必须时刻处于重心前后限的范围之间。式(16)为飞机在不同重量下的重心限制，其中minINDw和maxINDw分别为飞机在不同重量下所对应的重心包线前后限，而INDw为在不同重量下配载结果对应的指数，通过式(17)计算获得，即

(16)

w∈{TOW,LW,ZFW}

(17)

式中：BI为空机重指数；FIw为飞机不同重量时对应燃油指数；C1为缩小系数；CGDATUM为平衡基准点站位,对于给定航班为已知数据。

3 载重平衡问题求解

拟采用遗传算法来求解载重平衡问题，遗传算法是根据自然界的进化理论和遗传学说所创造的一种启发式算法。使用适者生存的原则来逐步逼近一个可行的近似解，这个过程使得新个体比原个体更能适应环境。图2是遗传算法流程图。

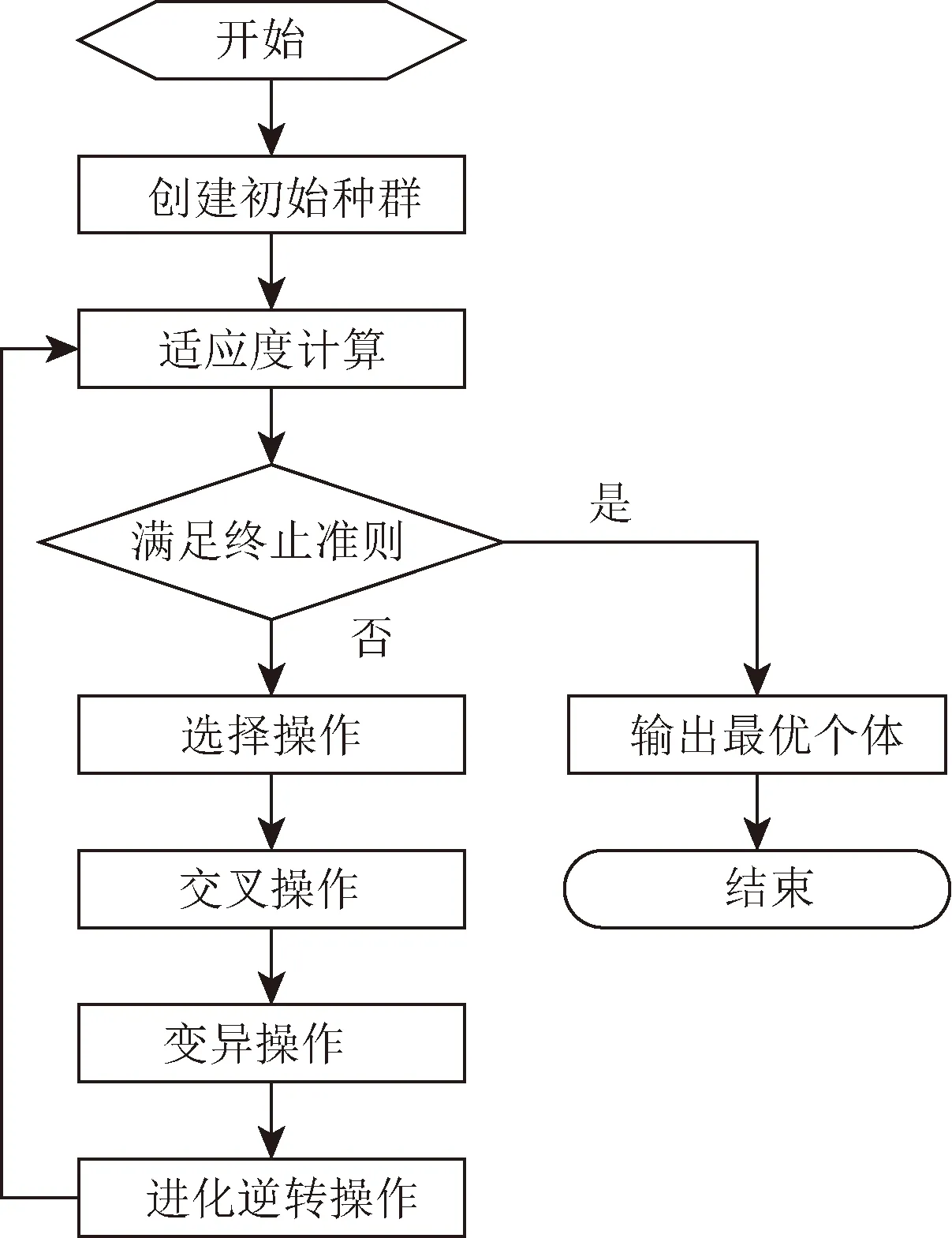
图2 遗传算法流程图Fig.2 Genetic algorithm flow chart

3.1 编码方式

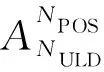
图3 编码方式示意图Fig.3 Schematic diagram of coding mode

3.2 适应度函数

由于将双目标函数转化为单目标函数之后，仍是求解模型的最大值因此将目标函数[式(5)]作为适应度函数。

3.3 选择算子

对于选择算子的设计在这里仍采用常见的轮盘赌，轮盘赌是指个体被选中的概率与适应度成正比，适应度越高，个体被选中的概率越大。对于该模型而言，假设种群个体数为P,Fp为其中某个个体的适应度值，那么个体被选择遗传到下一代的概率Pp为

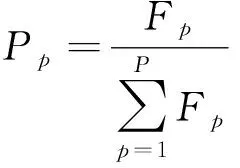
(18)

3.4 交叉算子

交叉操作是遗传算法最重要的操作，是产生新个体的重要来源，直接关系到算法的全局寻优能力，采用部分映射交叉，即在满足给定交叉概率下，随机生成某条染色体上交叉位置。具体操作如下。

随机产生两个[1,10]的随机数r1和r2，代表选择交叉的位置，比如r1=2、r2=4,如图4中灰色的位置，将第一个个体r1到r2之间的基因(即集装器序号)与第二个个体r1到r2之间的基因交换，交换之后如图5所示。

图4 交叉前示意图Fig.4 Schematic diagram of crossover

图5 交叉后示意图Fig.5 Schematic diagram after crossing

灰色部分表示交叉过来的基因，然而仔细观察后发现交叉过来的基因与原来其他位置上的基因可能会有重复，第一个装载方式重复基因的数目与第二个装载方式重复基因的数目是相同的(这里都是3个)，只需要把第一个装载方式重复的基因(用黑色标识)与第二个装载方式重复的基因做交换，即可以消除冲突。消除冲突之后的解如图6所示。

图6 解除交叉冲突示意图Fig.6 Schematic diagram for removing cross conflict

3.5 变异算子

变异算子的设计针对一个染色体(即个体)随机选取两个基因进行交换。例如图7的变异示意图，随机生成区间[1，10]的两个数r1、r2分别为3和8，然后将位置3和位置8互换基因。

图7 变异算子示意图Fig.7 Schematic diagram of mutation operator

3.6 进化逆转操作算子

在标准的遗传算法中是没有进化逆转操作算子的，为了加速进化在选择、交叉、变异之后加入的一个操作。进化逆转操作是具有单向性的，若逆转之后个体变得更优即适应度越大，则执行逆转操作，否则逆转无效。逆转算子在操作时仍是随机选择两个位置r1和r2,然后将r1和r2之间的基因进行反向排序。比如对于某个装载方式随机选择位置r1=3，r2=5，将其之间的基因按照相反顺序倒过来。具体操作如图8所示。

图8 进化逆转操作示意图Fig.8 Schematic diagram of evolutionary reversal operation

在文献[20-22]中，逆转算子的加入使得子代继承了更多的父代基因信息，由于只往好的方向逆转，因此在搜索最优解的能力比顺序交叉算子更强。

3.7 约束条件处理

在处理约束条件时运用文献[23]中的y-check思想，具体过程为将每次的解代入各个约束条件中进行判断。

约束(5)和约束(6)在编码方式上已经处理完成无需考虑。

约束(7)和约束(8)在生成初始解就进行判断，直到满足约束(7)和约束(8)初始解输出进行下一步工作。

计算目标函数，满足约束(9)～约束(17)输出解。

4 仿真实例

4.1 算例数据

某次航班任务执飞机型为B757-200F，飞行计划报显示此次飞行任务所带起飞油量10 000 kg，航段耗油量为8 000 kg，表1给出了B757-200F的基本参数包括3类最大重量等，表2是每个舱位所能容纳集装器的最大重量和高度，表3为待装载的集装器基本信息。

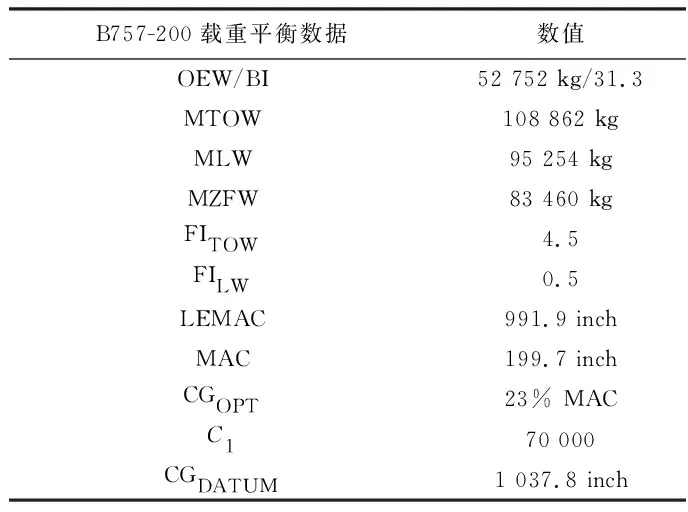
表1 B757-200F基本参数Table 1 Basic parameters of B757-200F

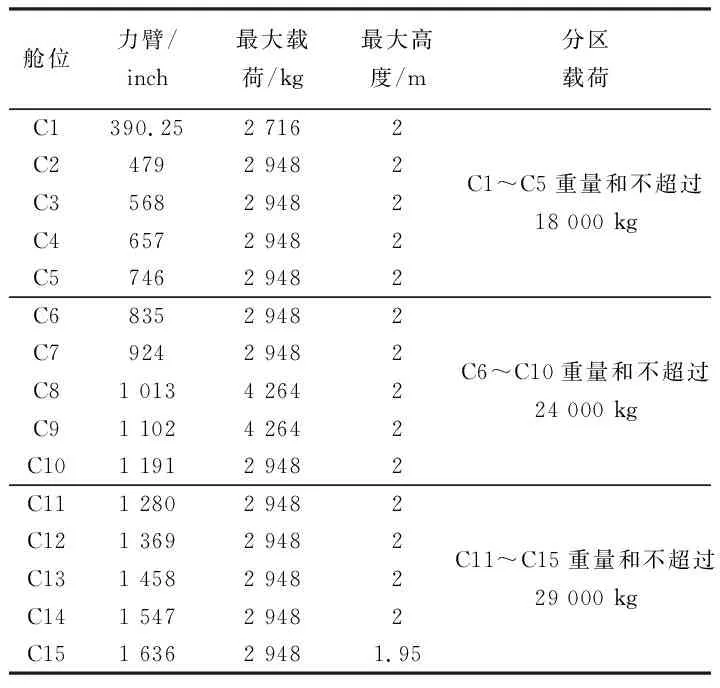
表2 货舱舱位约束Table 2 Constraints in main cargo compartment

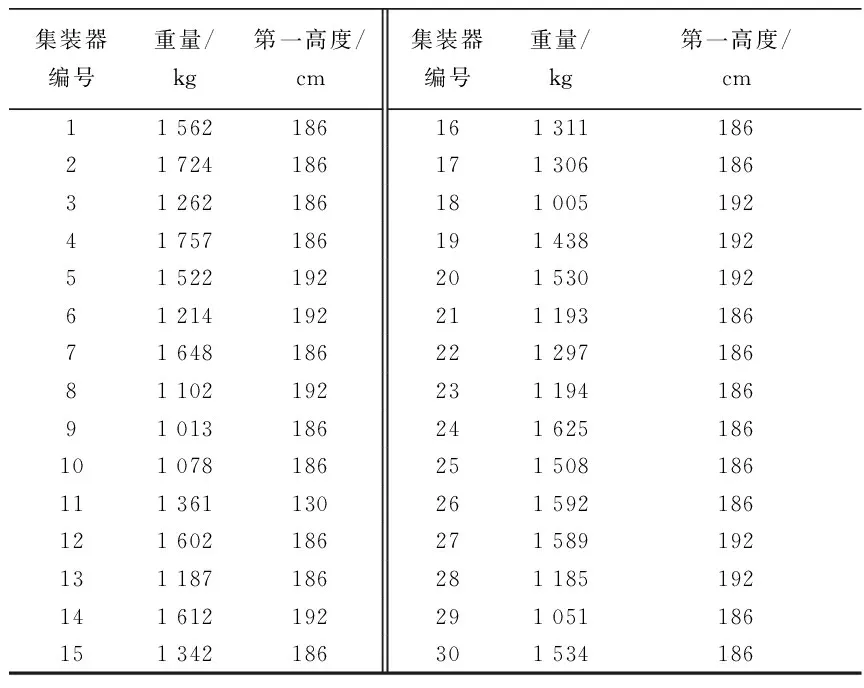
表3 集装器重量、高度Table 3 Weight and height of ULD

4.2 算例计算

此次算法程序在Visual Studio 2019 下运行，设ω1=0.8，ω2=0.2，在遗传算法中设置种群规模PS为200，遗传进化代数Gen为200，交叉率PC为0.9，变异率PM为0.1，表4为计算结果，可知遗传算法业载量平均为21 281 kg，重心偏移量平均为2.309%MAC，人工配载业载量为20 565.6 kg，重心偏移量平均为4.846%MAC。加入进化逆转算子后只加快了收敛速度，所计算的结果与普通遗传算法保持一致。

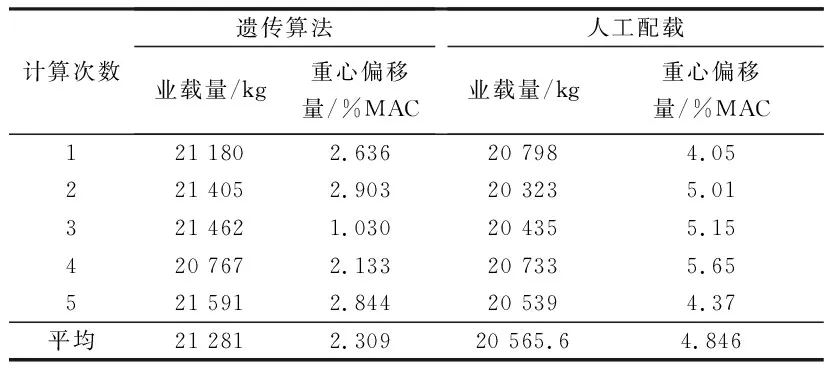
表4 计算结果Table 4 Calculation results

图9是引入进化逆转算子的遗传算法和普通遗传算法的适应度变化曲线，可以看出改进的遗传算法可以较快得到目标值。

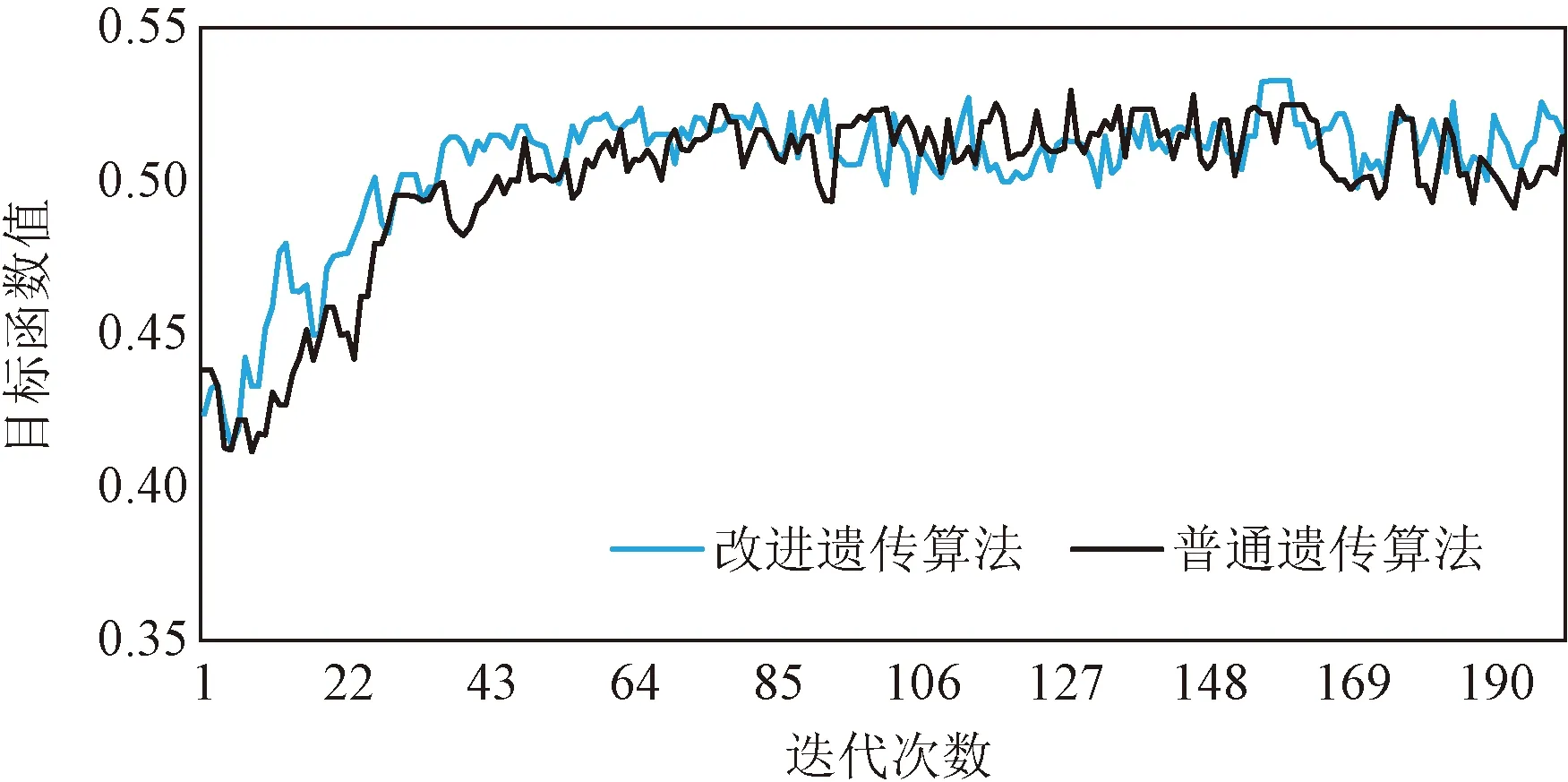
图9 遗传算法适应度变化曲线Fig.9 Fitness curve of genetic algorithm

图10和图11分别是在ω1=0.8下的重量箱线图和重心偏移箱线图，可以得出遗传算法都要优于人工计算，这是因为运用遗传算法时，可以快速排除质量较差的解，保留高质量的解，而人工配载一般根据经验，不具有高效性。

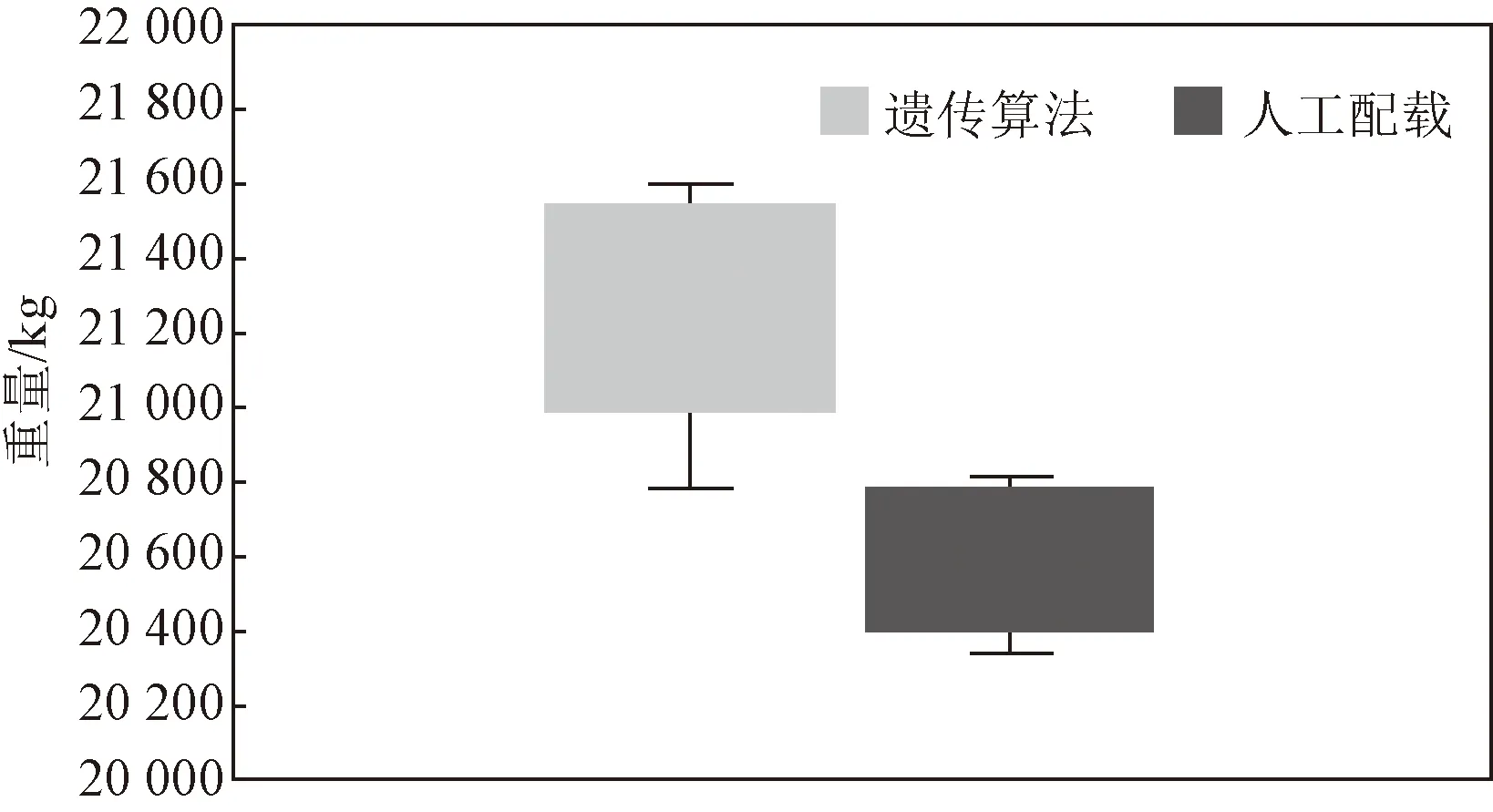
图10 重量箱线图Fig.10 Weight box diagram

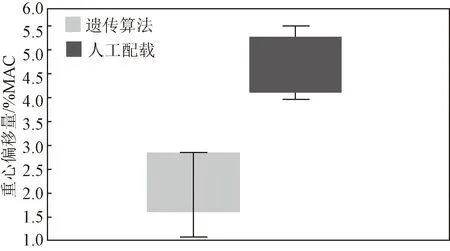
图11 重心偏移箱线图Fig.11 Boxplot of center of gravity deviation

4.3 多目标权重分析

为验证算法的有效性，拟多次调整多目标权重的取值。表5为在不同ω1下所计算得到的业载及重心，为保证数据的有效性，同一ω1下计算10组取均值得到。

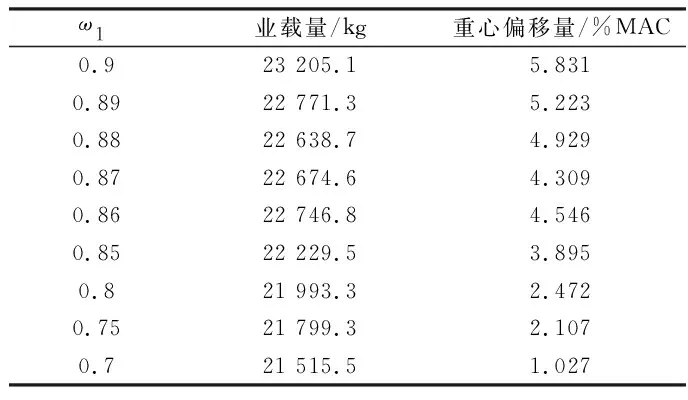
表5 不同ω1下的业载及重心偏差Table 5 Payload and center of gravity deviation under different ω1

在每个权重下计算多次得到图12的业载量和重心偏移量变化曲线，随着权重ω1的减小，业载量呈降低的趋势；在ω1从0.9减小到0.67过程中，重心偏移量呈接近目标重心的趋势。因此在实际情况下，各航司可以根据需要来选取不同的权重ω1满足需求。

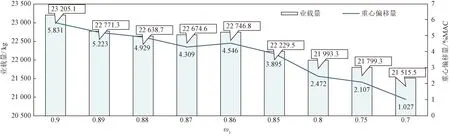
图12 不同ω1下的业载及重心偏差Fig.12 Payload and CG deviation under different ω1

5 结论

载重平衡工作在地面保障工作中发挥了重大作用。针对航空公司目前所存在的问题，如何获得一个可行的装载优化方案，建立了民航飞机货舱载重平衡模型，并运用改进的遗传算法进行求解。对B757-200F进行实例计算结果显示，平均业载可达21 281 kg，平均偏移量为2.31%MAC。由于所选机型为窄体机，在今后的研究工作中可以考虑宽体机的载重平衡问题，同时在重心优化上可以考虑将重心包线作为目标函数，来避免使用重心偏移量作为目标函数使得飞机重心偶然超出重心范围。