改进恒定时间间隔算法的无人汽车的队列控制

2022-02-03白倬宁尹逊和陈丽红

北京交通大学学报 2022年5期

白倬宁，尹逊和，陈丽红

（1.北京交通大学电子信息工程学院,北京 100044；2.中国机械工程学会,北京 100048）

随着道路货物运输量和家用汽车保有量的持续增长，几乎所有城市都面临着交通拥堵、空气污染和交通事故等严峻的问题.智能交通系统［1-2］（Intelligent Transportation System，ITS）的发展为上述问题提供了有效的解决方案.无人汽车车队的队列控制技术作为智能交通系统的重要组成部分，它使车队中的多个车辆以较小的安全距离行驶，能够缓解交通拥堵，同时在一定程度上避免交通事故的发生.因此，无人汽车的队列控制技术受到越来越多的学者和工程技术人员的关注.

无人汽车队列控制技术中的关键部分之一是行车间距的确定.由于车队中的车辆相互耦合，任何扰动引起的误差都有可能使整个车队变得不稳定，甚至发生安全事故.传统的期望车间距算法［3］包括固定间距算法（Constant Spacing Policy，CSP）和可变间距算法（Variable Spacing Policy，VSP），其中可变间距算法又分为恒定时间间隔（Constant Time Gap，CTG）算法和可变时间间隔（Variable Time Gap，VTG）算法.

在早期的研究中，固定间距算法最为常用，车辆间的期望动态间距为固定值，根据驾驶员的经验确定，与被控制车辆的速度无关.固定间距算法对车辆间信息交互的可靠性和实时性要求较高，当车辆间的通信受到影响时，则无法保证车队的队列稳定性，更不适用于现实中复杂多变的交通状况.

可变间距算法中的恒定时间间隔算法是在针对微观手动驾驶行为提出的安全距离模型［4］的基础上设计的，其中车辆间的期望动态间距与本车的速度成正比例关系.这种算法克服了固定间距算法对车辆间通信的实时性和可靠性要求高的问题，易于设计，并且能够确保单车及车队的稳定性.但在车速较低时，由于车间距较小，如果发生紧急制动的情况，则无法保证车辆的安全性.在此基础上，文献［5］根据前车和本车的相对速度，提出了一种可变时间间隔算法，该算法考虑了本车与前车的相对速度对期望动态车间距的影响：前车加速时期望动态车间距适当减小，前车减速时期望动态车间距适当增加，以保证车辆的安全性.但其对车辆间通信的依赖性较高，且在频繁变速的交通状况下，无法保证车队的稳定性.

近些年来，研究人员在传统的期望车间距算法上进行了改进，并取得了一系列成果.文献［6］以不同期望车间距算法的车辆组成的车队为研究对象，设计了虚拟的期望车间距算法，代替前车采用的未知期望车间距算法；然后，根据车队的递归模型推导出异质车队的稳定性条件，由此设计的队列控制结构能够实现对具有不同期望车间距算法的特殊车队进行控制.文献［7］将固定间距算法和恒定时间间隔算法相结合，以同时满足车辆低速行驶时的安全性和道路的通行效率.文献［8］将时间间隔算法分为加速阶段和减速阶段：当前车加速或匀速行驶时，采用传统的可变时间间隔算法；而当前车减速时，则根据减速的持续时间和速度的变化量调整加速权值，以增加减速条件下两车之间的相对距离.文献［9］在恒定时间间隔算法中引入前车的加速度信息，以减小时间间隔的下限，从而使期望动态车间距变得更小.文献［10］提出一种考虑执行机构时间常数的期望间距算法，并保证所有车辆跟踪相同的随空间变化的期望车速，例如车队在爬坡时的期望速度.但在算法的设计过程中，未考虑车辆间网络通信的延时所带来的影响.文献［11］在考虑交通流稳定性的二次车距算法的基础上，提出了指数车间距算法，在保证车队的队列稳定性的同时，提高道路交通流量.秦严严、胡兴华等［12］根据混合交通流稳定域的解析结果，提出了可变协同自适应巡航控制（Cooperative Adaptive Cruise Control，CACC）时间间隔算法，即从整个混合交通流的角度，在不同驾驶类型的车的比例下，所有CACC 车辆的期望的车间距统一发生变化.文献［13］为保证车辆在低速工况下的安全性，在恒定时间间隔算法的基础上考虑前车与本车的相对速度，从而在全速域都能保持车辆的安全性；同时，为防止车间距过大或过小，采用饱和函数对车间距进行限制，最大间距设定为100 m.文献［14］设计了由30 名驾驶员分别在12 种时间间隔下进行模拟驾驶的实验，研究影响恒定车头时距的主要因素，如，道路的交通效率、车辆的安全性和驾驶员的状态，并建议在不同的驾驶条件下选择不同的时间间隔.文献［15］针对在车队行驶过程中出现的车辆间通信中断的情况，提出了将协同自适应巡航模式切换至自适应巡航（Adaptive Cruise Control，ACC）模式的方法，可以降低车辆间通信中断对整个车队的影响，但由于车队的期望车间距设定的较大，会占用较多的道路容量.

为使期望车间距算法和控制策略更好地满足车队在实际行驶中对安全性和稳定性的要求，本文作者提出考虑路面附着系数的恒定时间间隔算法，并假设发生本车无法接收前车的加速度信息的情况，直至两车减速至静止，以此来计算最小安全车距，得到改进的恒定时间间隔算法.本文提出的改进恒定时间间隔算法能够保证车队在附着系数较低的路面上低速行驶时避免发生碰撞.然后，简要介绍了现有的车辆动力学模型.所设计的控制器考虑了相邻两车间的车间距误差、相对速度、相对加速度，并根据车队的队列稳定性条件推导出控制器增益的取值范围.采用本文的队列控制方法的车队发生本车无法获取前车加速度信息时，在无需切换控制器的情况下，仍能保证车间距误差的较快收敛和车队安全行驶.最后，通过对4 辆车组成的车队进行仿真分析，验证了本文提出的改进恒定时间间隔算法和车队控制器的有效性.

1 期望的车间距算法

1.1 传统的恒定时间间隔算法

恒定时间间隔算法最早由D.Swarrop 提出［16］

式中：dw为本车与前车的期望的动态车间距，m；vi(t)为本车的速度，m/s；th为时间间隔，s；dl为静态车间距，m，指当车队减速至静止时，相邻两车的车间距，其值一般被设定为一个车身的长度，其作用相当于为紧急制动等突发情况预留的安全裕量.

分析式（1）可知，期望的动态车间距dw和本车速度vi(t)呈正比，当本车的车速较快时，期望的动态车间距较大，可以保证当前车紧急制动时本车有足够的距离采取紧急措施，防止发生碰撞.但在车速较低的情况下，期望的动态车间距相应较小，如果路面附着系数较低，如雪地、潮湿的公路，由于车辆间没有充足的制动距离，容易发生碰撞事故.需要注意的是，算法中的“本车”仅限于车队中的跟随车辆，其车速趋向于领航车的稳态车速.

1.2 最小安全车距的计算

最小安全车距最早用于汽车安全车距预警系统或主动刹车系统.为避免车队在附着系数较低的路面上低速行驶时发生碰撞事故，考虑多种路面的附着系数，并假设本车无法持续获取前车加速度信息的情况计算最小安全车距，以此来代替恒定时间间隔算法中的静态车间距dl.

路面附着系数［17］是影响汽车制动距离的重要因素之一，附着系数是指轮胎在不同路面的附着能力，包含峰值附着系数和滑动附着系数.附着系数的最大值就是峰值附着系数，而汽车抱死滑动时的附着系数称为滑动附着系数.通常滑动附着系数比峰值附着系数小15%～20%，在计算时一般采用滑动附着系数.

如图1 所示，对汽车制动时的车轮进行受力分析，其中，假设汽车质量为m（kg），Fxb为制动力（N），G为汽车的重力（N），Fz为地面对车轮的法向反作用力（N），且与汽车的重力G的大小相等，方向相反（以汽车前进方向和汽车的重力方向为正方向）.若车轮在制动时抱死，此时，Fxb=-mamax=φFz，Fz=-mg，则

图1 汽车制动时车轮受力示意图Fig.1 Schematic diagram of the force on the wheel during braking

式中：φ为路面附着系数取值参考表1［18］；g为重力加速度，m/s2；amax为汽车制动时的最大减加速度，m/s2.

表1 典型路面的附着系数Tab.1 Adhesion coefficient of typical pavement

为提高车队应对紧急状况的能力，参考安全距离预警模型［19］，如图2 所示假设车队在行驶过程中发生本车无法持续获取前车加速度信息的情况来计算最小安全车距，得出

图2 最小安全车距示意图Fig.2 Schematic diagram of minimum safe distance between cars

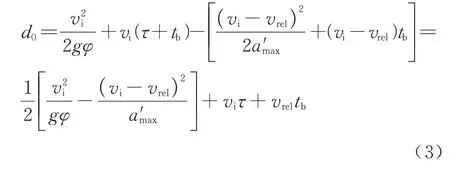
式中：d0为最小安全车距，m；vi为本车的速度，m/s；vrel为前后两辆车的相对速度，m/s；τ是车辆间通信延时，ms，参考文献［20］中定义的高优先性安全应用的要求和对车辆间的通信性能的规定，范围取为(0 ＜τ≤100 ms)，而出于安全方面的考虑，在计算d0时，τ取最大值100 ms；tb为制动系统的延迟时间，ms，取值为250 ms；为前车制动时的最大减加速度，m/s2，取值为8 m/s2；g为重力加速度9.8 m/s2.在实际应用中，路面附着系数φ可以根据不同路况实时获取，具体方法为：结合轮胎力学模型和状态估计算法对路况进行识别［21］，进而获取不同路面的附着系数.

主要方法为：将车辆视为质点，本车与前车分别位于A点和B点.假设从t=ti时刻起，本车无法获取前车的加速度信息，同时前车以最大的减加速度进行紧急制动，本车以恒定的减加速度减速行驶，当两车减速至静止时位于C点且刚好不会相撞，即车间距为零.

1.3 改进的恒定时间间隔算法

将最小安全车距d0代替式（1）中的静态车间距dl，可得改进的恒定时间间隔算法

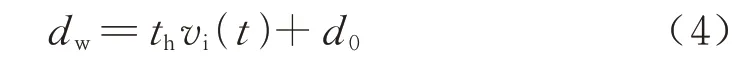
为防止车间距过大而带来的负面影响，如车辆间通信距离受限，道路利用率较低等问题，参考文献［20］中对车辆间的通信距离的规定，将期望动态车间距的最大值设定为150 m.

2 车辆动力学模型

本文的无人汽车车队结构见图3，虚线为信息传输方向.在简化的车辆动力学模型中，实际加速度和期望加速度之间的关系可用一阶惯性环节［22］表示

图3 无人汽车车队的结构Fig.3 Structure of unmanned vehicle platoon

式中：ai和adesi分别为第i辆车的实际加速度与期望加速度，m/s2；η为执行机构的时间常数，ms.

假设车队中的每辆车的动力学特性相同，车辆动力学模型为

式中：pi(t)、vi(t)、ai(t)为车辆i（i为车辆索引号，i=1，2，3，…，n）的实时位置、速度（m/s）、实际加速度；i=1 时表示领航车.式（6）中的车辆动力学模型已广泛用于队列控制系统的设计与分析［23］.

车队在行驶过程中，车辆位置满足

本车与前车的车头间距为

联立式（4）和式（8），可以计算车间距误差为

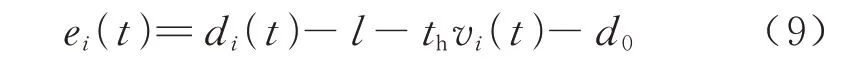
式中：ei(t)为车间距误差，m；l为车辆的长度，m.

3 队列纵向控制

队列纵向控制系统通常采用分层的控制结构［24］，上层控制根据车辆的状态信息计算出期望加速度，下层控制通过控制节气门开度或制动压力来跟踪上层控制计算的期望加速度.控制方框图如图4 所示.Δvi为相对速度；Δai为相对加速度；值得注意的是，领航车与跟随车的上层控制器不同.领航车作为整个车队的稳态速度的制定者，仅负责将自身的位置、速度和加速度信息传递给下一辆跟随车，所以其不具备跟随车中用于间距控制的上层控制器.

图4 队列纵向控制方框图Fig.4 Diagram of platoon longitudinal control

上层控制中，控制律设计为

式中：kp、kv和ka为车辆i的控制增益.车辆在正常行驶中，期望加速度在[-2.5，2.5]m/s2内可以保证乘坐舒适性［25］，且加速度的绝对值越小越好［26］.

为了跟踪上层控制计算的期望加速度adesi，下层控制中的期望发动机扭矩Te和期望制动力矩Tb计算为［27］

式中：r、f、m、C、A、ρ、δ分别为车轮半径（m）、滚动阻力系数、汽车的质量（kg）、空气阻力系数、汽车的迎风面积（m2）、空气密度(kg/m3)和旋转质量转换系数.

则期望的节气门开度θ和制动压力Pbrk为［28］

式中：ωe为发动机转速，r/min；kb为制动系数.由于发动机的转速、发动机的扭矩和节气门开度3 个参数的关系很难用明确的公式给出，因此，研究人员通常使用MAP 图，利用查表的方法，依据发动机的扭矩和转速反查出节气门的开度.

驱动与制动的切换策略［29］用于判断车辆是否进行加速或制动.切换策略根据实车试验数据获得，取怠速工况下不同车速所能达到的最大加速度作为加速度的切换值aswitch.为避免节气门和制动系统频繁切换，通常将加速度的切换值设定为一个范围作为过渡区间，过渡值一般取h=0.1 m/s2，则切换规则为1）当adesi＞aswitch+h时，车辆采取加速措施；2）当aswitch-h＜adesi＜aswitch+h时，车辆既不采取加速也不采取制动措施；3）当adesi＜aswitch-h时，车辆采取制动措施.

3.1 队列稳定性

为了满足车队的队列稳定性，则要避免车间距误差在向车队尾端传播时被不断放大，最终导致车队整体的不稳定，即队列中车间距误差传递函数在频域内应满足［30］

式中：Ei(jω)是ei(t)在频域的表达式.通过对车队的队列稳定性进行分析，可得出满足的条件的时间间隔th和控制器增益kp、kv、ka.

对车辆i，由式（6）和式（10）得

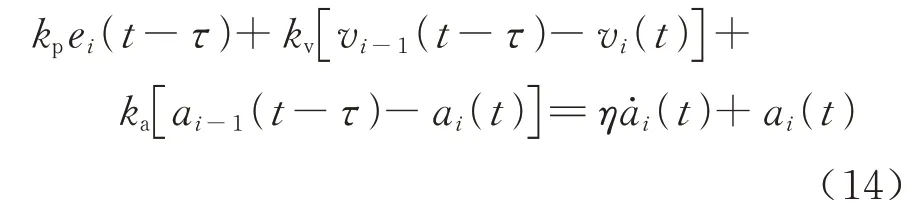
将式（9）代入式（14），求导可得

对式（15）两边进行拉氏变换，可得到相邻两车的速度的传递函数为

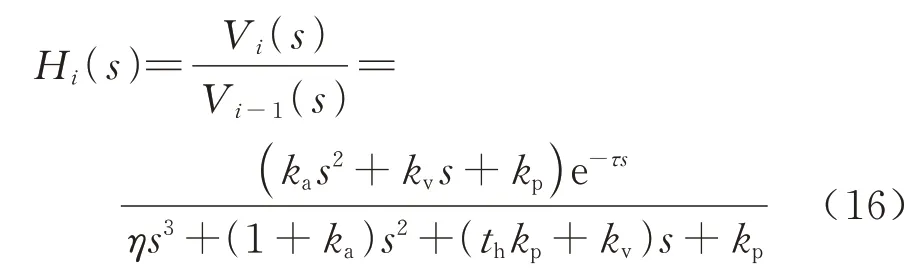
式中：Vi(s)为vi(t)的频域表达式.

将式（9）等式两边同时求导，并取拉氏变换，得

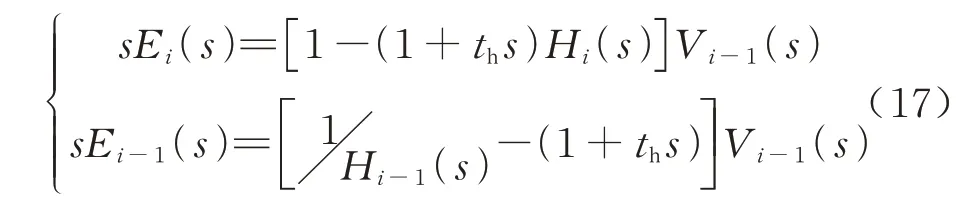
根据式（17）可得到相邻两车的间距误差的传递函数为

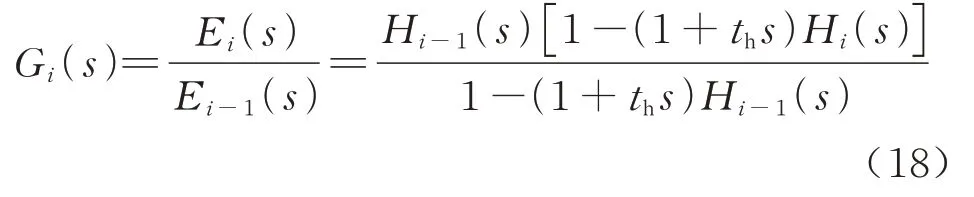
假设车队中每辆车的网络通信延时和执行机构时间常数均相同，此时Hi(s)=Hi-1(s)，则

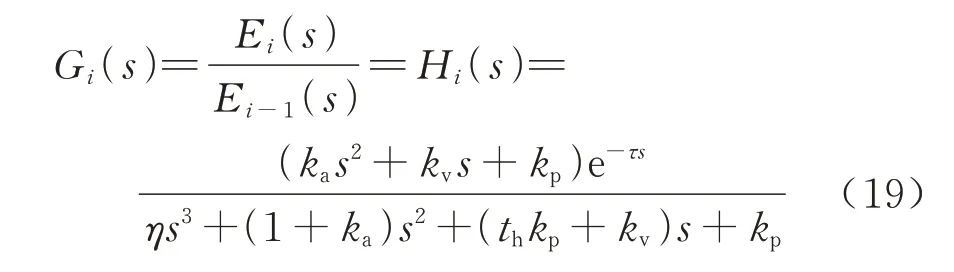
定义

当式（23）中ω各项系数不小于0 时，有b＞0 对任意ω＞0 成立.由此可得出队列稳定性条件为

当执行机构的时间常数η、时间间隔th和控制器增益kp、kv、ka满足式（24）中的关系时，车队在行驶中可以保证队列稳定.

3.2 车间距的稳态误差

通常，车队处于稳态时车间距误差应该收敛于零［32］，有

由拉氏变换的终值定理可知

定义ξ1(t)为在t时刻，领航车的速度vi(t)与稳态速度v0的偏差为

将式（28）和式（29）代入式（26）得

最后求得车间距稳态误差为

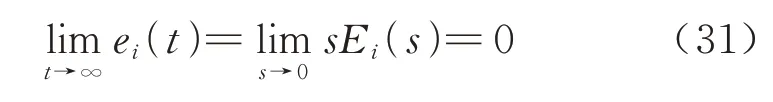
因此，车队在行驶中，车间距稳态误差收敛于零.

4 仿真结果与分析

为了检验本文提出的改进的恒定时间间隔算法和车队控制器的有效性，利用Matlab/Simulink 和VANETs 工具箱［33］对由1 辆领航车和3 辆跟随车构成的车队进行仿真.如图5 所示，其中“Leader_1”和“Follower_i”（i=2，3，4）分别代表领航车1 和跟随车i的网络节点，“input”和“output”分别表示车辆的输入信号和输出信号，“［p_i］”、“［v_i］”、“［a_i］”分别表示车辆i的位置、速度和加速度.前车的输出信号（位置、速度和加速度）通过无线网络传输后，作为本车的输入信号，例如，领航车1 的输出信号通过无线网络传输后，作为跟随车2 的输入信号.同理，跟随车2 的输出信号通过无线网络传输后，可作为跟随车3 的输入信号.无线网络模块的通信协议设置为IEEE 802.11p.VANETs 工具箱是一个包含车辆移动模型和车载网络模拟器的Simulink 库，主要包含车辆网络层、应用层、介质访问控制层和物理层.在使用时，用户可以通过将车辆网络堆栈中所需的模块拖放和连接在一起，来组成车辆网络节点.应用层模块集成了消息生成模块和跟车模型，用户可以结合软件对整车控制器进行设计并修改整车的参数，模拟车队的纵向控制.整车仿真模型由软件实现，通过软件在仿真开始前设定汽车的参数和控制器增益，整车控制器和期望力矩模型式（11）可以根据前车的状态信息计算并最终输出本车的加速度、速度和位置.汽车的参数见表2.

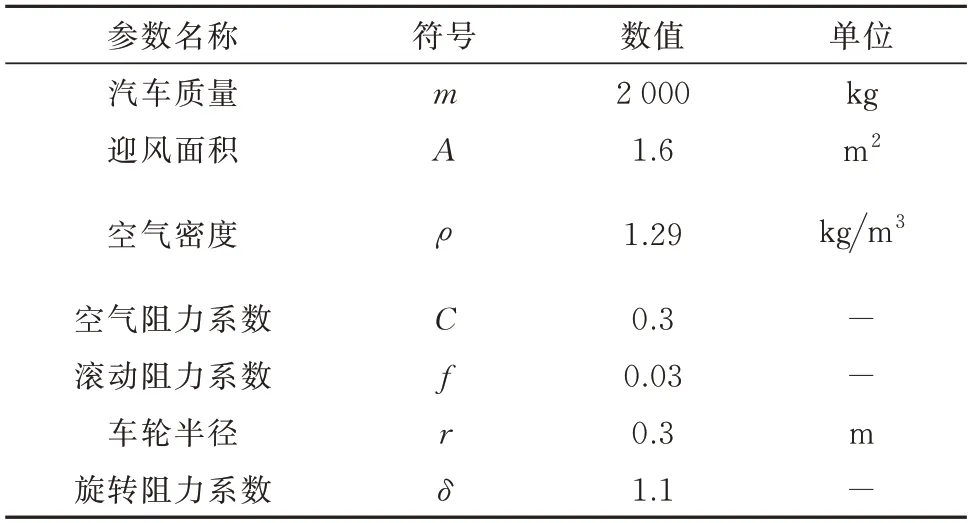
表2 汽车的参数Tab.2 Parameters of the vehicle

图5 车队仿真模型Fig.5 Simulation model of platoon

首先，为验证队列稳定性条件式（24）的有效性，对采用不同控制增益组合的车队的行驶情况进行仿真分析，假设车队在行驶过程中存在车间距误差，以考察车队的队列稳定性.车辆动力学模型式（6）中，执行机构的时间常数η=250 ms［27］，车辆间通信协议为IEEE 802.11 p，网络通信延时τ的范围为(0 ＜τ≤100 ms).车队的稳态速度设定为20 m/s（即，72 km/h），路面设置为干燥的沥青路，根据表1总结的典型路面的附着系数，路面附着系数可确定为φ=0.75.改进的恒定时间间隔算法式（4）中的时间间隔th=0.6 s，车身长度为5 m，分别取两组控制器增益［34］：1）kp=1.1、kv=1.2、ka=0.7（满足队列稳定性条件）；2）kp=1.1、kv=0.5、ka=0.7（不满足队列稳定性条件）.两种情况下的仿真结果如图6 所示.控制器增益的获取方法为：首先，参考文献［34］确定控制增益kp=1.1，然后将控制增益kp、执行机构的时间的常数η=250 ms 和间距算法中的时间间隔th=0.6 s 代入队列稳定性条件式（24）中，可分别得出kv的取值范围为kv＞0.96，ka的取值范围为ka＞0.51.然后，采用试探法初步设定kv=1，ka=0.6，观察仿真结果中车队的行驶状况和车间距误差，如果结果不理想则微调kv的数值，当不同增益组合下的最大车间距误差的标准差小于0.05 m 时，取增益的中间值作为仿真参数，进而确定kv=1.2.最后，采用同样的方法微调ka的数值，并确定ka=0.7.

如图6 为采用不同控制器增益组合的车队行驶情况.根据式（4）计算出车队稳态行驶时的期望车间距为18 m，在初始时刻，每辆车保持以20 m/s 的速度行驶，假设1 号领航车和2 号跟随车之间存在4 m 车间距误差.图6 中（a）和（b）分别是控制器增益满足队列稳定性条件式（24）时的车辆速度和车间距误差变化情况，可以看出在初始时刻存在4 m 车间距误差后，跟随车辆可以较好地跟踪前车的速度，且车间距误差在向车队尾端传播时的最大值为2.2 m，并随着时间的增长最终收敛于0 m，表明车队可以保持稳定行驶.图6 中（c）和（d）分别是控制器增益不满足队列稳定性条件式（24）时的车辆速度和车间距误差变化情况，结果表明车速产生了较大范围的波动，且跟随车3 和4 之间的车间距误差在第21 s 时达到最大值为6.1 m，说明车间距误差在向车队尾端传播的过程中发散，车队无法稳定行驶.

图6 不同控制器增益下的仿真结果Fig.6 Simulation results under different controller gains

然后，为了验证采用最小安全车距改进的恒定时间间隔算法，能否在路面附着系数较低的情况下保证车辆间避免发生碰撞，将本文方法与文献［13］中提出的考虑本车与前车相对速度的期望车间距算法进行对比仿真.假设文献［13］中的车队与本文相同，车辆动力学模型式（6）中，执行机构的时间常数η=250 ms，网络通信延时τ的范围为(0 ＜τ≤100 ms).为了检验车队在潮湿土路上低速行驶时期望车间距算法的有效性，车队的稳态速度设定为13 m/s（即，46.8 km/h），根据表1 总结的典型路面的附着系数，潮湿土路的路面附着系数可确定为φ=0.4.式（4）改进的恒定时间间隔算法中的时间间隔th=0.6 s，车身长度为5 m，根据队列稳定性条件式（24），控制器增益设置为：kp=1.1、kv=1.2、ka=0.7.图7 为车队中相邻两车间距的变化情况.

如图7（a）所示，考虑到潮湿土路的路面附着系数较低，通过式（3）计算得出最小安全车距为13.2 m，再根据式（4）将期望的动态车间距确定为20 m.在初始时刻，每辆车保持以13 m/s 的速度行驶，假设1 号领航车和2 号跟随车之间存在4 m 车间距误差.第30 s 时，由式（9）计算得到的车间距误差收敛于0 m，通过式（8）计算的车间距稳定在20 m 左右，且车辆间未发生碰撞；如图7（b）中，文献［13］由于没有考虑路面附着系数对制动距离的影响，其采用的期望车间距算法将期望的动态车间距计算为12 m.在初始时刻，每辆车保持以13 m/s 的速度行驶，假设1 号领航车和2 号跟随车之间存在4 m 车间距误差.第28 s 时，2 号跟随车和3 号跟随车的间距为0 m，表示发生了碰撞.由此可得出结论：在路面附着系数为0.4 的潮湿土路等较滑的道路上，采用最小安全车距改进的恒定时间间隔算法可以保证车队的安全行驶，避免发生碰撞事故.

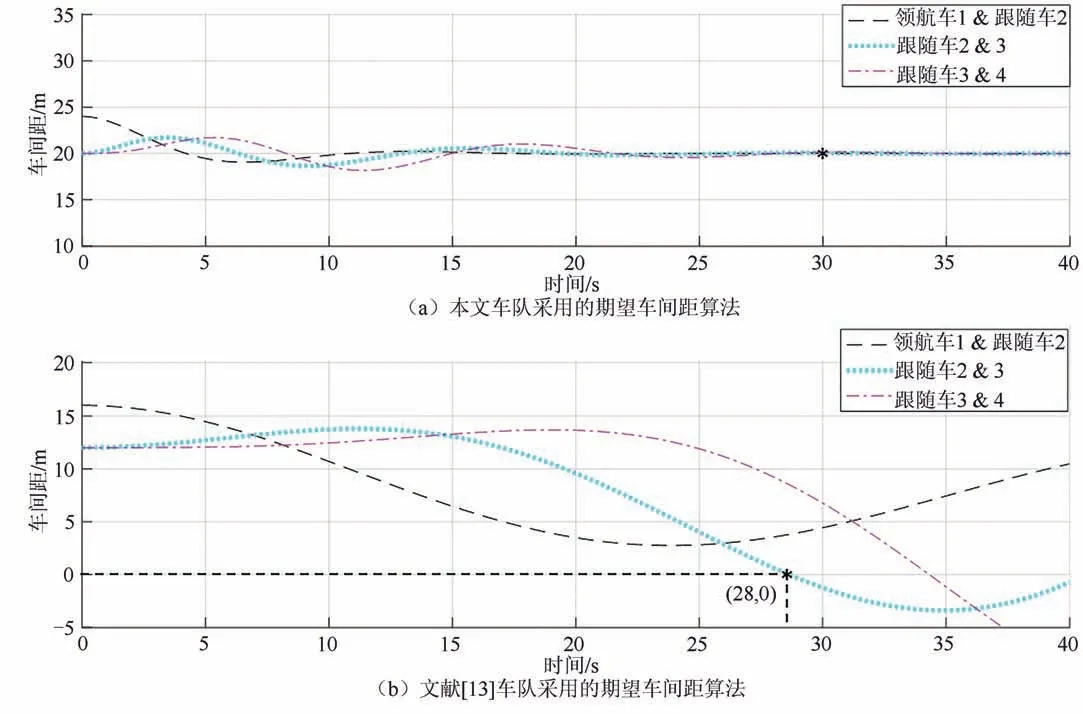
图7 车间距的仿真结果Fig.7 Simulation results of the distance between vehicles

最后，对车队行驶过程中因外来车辆插入而前车紧急制动，且本车无法持续接收到前车的加速度信息的情况进行仿真.网络通信延时τ的范围为(0 ＜τ≤100 ms)，执行机构的时间常数η=250 ms.如果不考虑车载通信设备故障或车辆受到网络攻击等情况，车辆间很少出现本车长时间无法接收到前车加速度信息的情况，为使仿真结果更明显，将本车无法获取前车加速度信息的持续时间设定为3 s.为了验证车队在正常路面上中速行驶时期望车间距算法的有效性，并保证仿真结果的多样性，将路面设定为干燥的沥青路，路面附着系数φ=0.75，车队的稳态速度为17 m/s（即，61.2 km/h），时间间隔th=1 s，车身长度为5 m，控制器增益设置为：kp=1.1、kv=1.2、ka=1.

图8 为车队在行驶过程中车间距、车间距误差和加速度的变化情况.在初始时刻，通过式（4）计算得到每辆车之间的期望动态车间距为20 m.在第4 s时，2 号跟随车的前方10 m 处突然插入外来车辆，2 号跟随车随即采取减速.同时，3 号跟随车无法接收到2 号跟随车的加速度信息，持续时间为3 s，为避免发生碰撞事故，3 号跟随车与4 号跟随车采取减速.第25 s 时，相邻两车的车间距误差均为0 m，外来车辆成为车队中的一员，与其他车辆保持相同的稳态车速和车间距行驶.图8（a）表明在第4 s 3 号车无法获取2 号车的加速度信息后，相邻两车的车间距均未小于零，说明整个车队未发生碰撞事故，车队可以保持安全行驶.图8（b）表明2 号跟随车与3 号跟随车之间的车间距误差相比于3 号跟随车与4 号跟随车之间的车间距误差较大，在第6.6 s 时，车间距误差最大为3.9 m，但所有车辆间的车间距误差在向车队尾端传播的过程中逐渐收敛，并最终在第27 s 时收敛于0 m，表明车队能够保持队列稳定.图8（c）中，当3 号、4 号跟随车在加速时，4 号车的加速度的绝对值最大，其值为0.75 m/s2；当3 号、4 号跟随车在制动时，3 号车的减加速度的绝对值最大，其值为0.56 m/s2，均处于[-2.5，2.5]m/s2的区间内，满足第三节中的乘座舒适性条件.

图8 （本文的方法）车间距、车间距误差和加速度的变化情况Fig.8 Changes in vehicles distance,the error of the vehicles distance and acceleration (method of the paper)

在现有的方法中，当车队在行驶过程中突然发生本车无法获取前车的加速度信息的时，通常采取协同自适应巡航控制与自适应巡航控制模式切换的方法.假设文献［15］中的车队与本文相同.图8 表明车队在行驶过程中车间距、车间距误差和加速度的变化情况.在初始时刻，车队中的每辆车保持17 m/s 的车速、22 m 的车间距稳定行驶.在第4 s 时，2 号跟随车的前方10 m 处突然插入外来车辆，2 号跟随车随即采取减速，同时，3 号跟随车无法接收到2 号跟随车的加速度信息，持续时间为3 s.为避免发生碰撞事故，3 号跟随车与4 号跟随车采取减速.第50 s 时，相邻两车的车间距误差均为0 m，外来车辆成为车队中的一员，与其它车辆保持相同的稳态车速和车间距行驶.图9（a）显示，在3 号车无法接受2 号车的加速度信息后，车队中相邻两车的车间距均未小于零，说明整个车队未发生碰撞事故，车队可以保持安全行驶.由图9（b）可知，2 号跟随车与3 号跟随车之间的车间距误差相比后方车辆的车间距误差较大，且在第8 s 时，车间距误差最大为4.9 m，但所有车辆间的车间距误差在第50 s 时收敛于零.图9（c）中3 号和4 号跟随车在加速时，4 号车的加速度的绝对值最大，为0.91 m/s2；在制动时，3 号车的减加速度的绝对值最大，为 0.9 m/s2，均处于[-2.5，2.5]m/s2的区间内，满足乘座舒适性条件.

图9 （文献[15]的方法）车间距、车间距误差和加速度的变化情况Fig.9 Changes in vehicles distance,the error of the vehicles distance and acceleration (method of Ref.[15])

图8（a）与图9（a）表明，采用本文方法的车队的期望动态车间距保持为20 m，相比文献［15］方法中车队采用22 m 的期望动态车间距，占用更小的道路容量，同时能够避免碰撞事故.图8（b）与图9（b）相对比可知，采用本文方法的最大车间距偏差率为19%，低于文献［15］方法的最大车间距偏差率22.27%，车队的稳定性较强.图8（c）和图9（c）相比，3 号车与4 号车的最大加速度的绝对值较小，乘坐舒适性更好.仿真结果表明了本文的改进的恒定时间间隔算法和车队控制器的有效性.