基于SM-LADRC 的高速列车自动驾驶速度控制

2022-02-03梁乐观牛宏侠

北京交通大学学报 2022年5期

梁乐观，牛宏侠

(兰州交通大学 a.光电技术与智能控制教育部重点实验室，b.甘肃省高原交通信息工程及控制重点实验室，c.自动化与电气工程学院，兰州 730070)

随着珠三角城际铁路列车运行控制系统运行经验的持续积累，以及高速列车运输效率的不断提高，列车目标从更快地运行转向更好地决策，即自动化向智能化转换的趋势.在高速铁路既有的列控系统中叠加自动驾驶（Automatic Train Operation，ATO）功能，是近年来各研发单位的突破难点之一［1］.车载设备中的ATO 系统通过精确跟踪先验知识生成的理想目标速度-距离曲线来完成最优控制，旨在进一步确保准时性、优化乘客舒适度、提高区间运输效率.而在时变动态的影响下，列车运行过程中内部参数的不确定变化和运行线路上外部环境的未知扰动，将导致与实际运行速度存在较大误差，降低跟踪精度，影响上述性能指标.所以精确跟踪列车自动驾驶的速度具有举足轻重的意义.文献［2］应用预测模糊PID 跟踪城轨列车运行曲线.文献［3］采用神经网络PID 控制器跟踪列车速度，显示其误差为±4 km/h，控制效果不明显.文献［2-3］中PID 控制器追踪列车速度时，在外界强干扰作用下存在鲁棒性差、稳定性不高等缺点.文献［4］为了补偿自动驾驶精确进站停车的非线性扰动，引入自适应模糊滑模控制，文献［5］将非奇异控制律的滑模控制应用于最少传感器的跟车控制系统.但滑模控制的优缺点较为明显：优点是系统对扰动和参数摄动完全无关，响应速度较快；缺点是不可避免地存在因空间滞后和时间延迟形成的抖振现象.文献［6］提出传统ADRC 的电流解耦控制策略以改善列车运行的稳定性.文献［7］利用ADRC 方法实现了良好的控制效果，但控制器参数过多不利于系统实时调整.文献［8］将自适应线性自抗扰用于磁悬浮球，优化了观测器带宽参数难以调整的问题.文献［9］表明LADRC 具有广泛的适用性，在众多复杂系统工程中已得到成功应用.文献［10-12］证明了将滑模控制和自抗扰控制结合后在系统工程中的应用价值.

鉴于此，本文作者首先采用LADRC 通过线性扩张状态观测器（Linear Extended State Observer，LESO）将列车受到的总扰动实时估计并补偿，使系统镇定在平衡点，保证控制精度的同时精简控制参数，但响应速度相对滑模控制较慢；之后，为提升响应速度和减弱抖振，对SMC 提出改进指数趋近律和引入连续函数两方面的改进；最后，用改进的SMC设计非线性误差反馈律，完成SM-LADRC 控制器的设计.仿真结果表明，改进后的滑模线性自抗扰控制器在列车受到内、外部干扰的情况下也能很好的跟踪控制指令.

1 列车单质点模型

构建列车模型是研究的基础，本文将整个列车视为一个质点，对其进行牵引力、制动力和阻力的受力分析，即不考虑车辆之间的相互耦合力，可得出单质点模型为

式中：u表示列车单位牵引力；x1表示实际列车位移；（或x2）表示实际列车运行速度表示实际列车运行加速度；wj为单位基本阻力；a1、a2、a3分别为列车运行时的基本阻力系数；wf为线路附加阻力；r为列车回转质量系数；g是重力加速度，取值为9.81 m/s2.

为了方便控制器设计，式（1）可改写为以下的线性二阶系统

式中：b=为该系统的控制量；y为系统输出值；x(t)=[x1(t)，x2(t)]；ψ为系统的外部干扰，设D为ψ的上界，且满足|ψ|≤D.

本文的控制目标是，针对高速列车速度跟踪控制，设计滑模自抗扰控制器u，使得速度、位移误差能够渐近稳定且具有优良的动态品质.

2 SM-LADRC 控制器设计

将系统的总扰动，即模型中的内部未知和外部干扰，通过LESO 估计出来，然后在控制律中进行补偿，并将SMC 用于非线性误差反馈律的设计.当输入速度指令Vd时，通过该控制器使得速度误差趋于0，以达到精确跟踪.本文设计不需考虑滤波，故不设跟踪微分器，传统ADRC 速度控制器中状态观测器和控制律的可调参数分别为6 个和5 个，共11 个，具体参数详见文献［7］；而本文的SM-LADRC 在保证提高跟踪精度的同时，将可调参数减少至8 个.SM-LADRC 控制器结构框图如图1 所示.图1 中，SMC 模块表示滑模非线性误差反馈控制律；运行列车模型如式（1）所示；z1、z2、z3分别表示观测器观测x1、x2、x3的输出值，b0表示控制输入系数.

图1 SM-LADRC 控制器结构框图Fig.1 Block diagram of SM-LADRC controller structure

2.1 线性扩张状态观测器LESO 设计

定义x3=f(t)+ψ，控制器增益b＞0 且数值已知；假设x3可微，且=p，现将x3扩张成一个新的状态变量，则系统状态式（2）扩张后如下

将文献［7］ADRC 中的fal(*)函数用误差估计e1替换，构造满足系统的LESO 为

式中：e1为误差估计，选取适当的观测器增益值β1、β2、β3，就可实现LESO 对系统中各个状态变量的监控.

2.2 SMC 非线性误差反馈控制律设计

传统ADRC 中的非线性误差反馈控制律模块，采用控制参数较多、参数整定困难的非线性函数.所以本文将滑模变结构控制引入该模块，在简化参数的同时改善系统的控制响应性能，同时设置实时反应列车跟踪效果的反馈控制参数.首先根据二阶系统设计滑模面，然后通过仿真试验对比选择最适合的趋近律以改善控制器的动态品质，最后推导出控制律.

定义xd为位移期望值，列车位移追踪误差用e表示，速度追踪误差用表示，则系统误差方程为

结合式（1）、式（2）、式（5）及改进后的趋近律，可推导出滑模控制律为

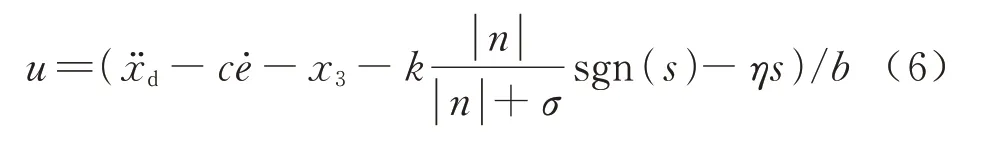
又经仿真试验得知，趋近律中的符号函数sgn(s)具有不连续性，导致控制信号中出现高频抖振的概率很大.所以将符号函数用连续函数h(s)=s/(|s|+w)替代，以达到再次减弱抖振的目的，式中w 是很小的正常数.

2.3 控制器参数整定

SM-LADRC 中，LESO 的参数主要w0、b、b0，SMC 误差反馈律中的参数有c、k、w、σ、η.其具体调整方法如下：

1）LESO 参数整定.

根据文献［13-15］中的带宽法整合LESO 参数，并选取决定系统稳定性和主导其暂态特性的闭环极点-w0，w0在这里表示观测器的带宽，是观测器部分唯一需要整定的参数，简化了参数调试工作.其合适的取值可使z3很好地估计扰动值，从而推算出观测器增益β1=3w0，β2=3w02，β3=w03，满足LESO 对应的特征方程s3+β1s2+β2s+β3=(s+w0)3是Hurwitz 的，LESO 能够收敛.调参过程中需注意的是，虽然带宽w0越大，线性扩张状态观测器的跟踪速度越快，但同时容易出现控制器输出过于饱和现象，所以要适当选择参数值；动车组车型决定了r的值，然后可求得b值.参数b0与b的值越接近，则系统越稳定，控制器性能越好.

2）SMC 反馈律参数整定.

作为sgn(s)的增益系数，-值越大，系统抗干扰能力就越强，则σ取小值，k取较大值，但k越大，引起的抖振现象就越明显；η主要控制趋近的动态过程，所以调整k、η值时要同时考虑趋近过程动态品质和抖振；滑模面参数c越大，系统响应速度越快，但过大的c值又会引起抖振；w是很小的正常数.综合考虑以上参数对系统的影响，在仿真过程中，根据控制器跟踪效果调试参数值，使其跟踪性能最佳.

2.4 控制器稳定性分析

设=g(x)，且|g(x)|=τ，即g(x)有界.根据带宽法求出的β1、β2、β3值和式（4）可得出误差系统的稳态误差为

结合LADRC 和SMC 的优点构成的SMLADRC 控制器，其系统应满足有界且稳定的要求.根据选取的滑模面，定义Lyapunov 函数

式中：k、τ、c、w0均为正数，只要参数的取值满足kw02-6τ(c+w0)＞0，则≤0.于是，系统会在规定的时间范围内到达滑模面，然后沿着s=+ce(c＞0)运动，跟踪误差便会在有限时间内收敛到零.

3 系统仿真及结果分析

3.1 系统仿真

本文的研究对象为CR400AF 型智能动车组，仿真时需要的动车组参数，见表1.

表1 CR400AF 型动车组参数Tab.1 Parameters of CR400AF EMU

该试验仿真过程假设在平直线路运行，所以wf取值为零.依据上述的SM-LADRC 控制方法，结合式（1）的单质点模型和CR400AF 动车组参数，搭建的Simulink 仿真如图2 所示.图2 中，Vd模块中加载式（9）的理想速度曲线命令，u模块中加载式（6）的滑模控制律命令，x3模块中加载内外部扰动命令，LESO 模块中加载线性扩张状态观测器命令，仿真结果保存到File 中.

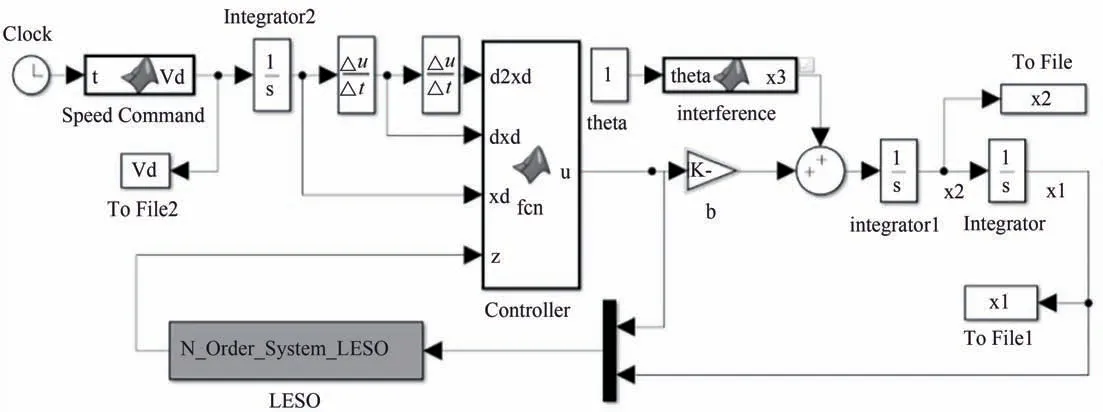
图2 搭建SM-LADRC 速度控制仿真Fig.2 Simulation of speed control based on SM-LADRC

现引用列车速度控制文献中常用的一条速度指令曲线［16］，并依据曲线轨迹，对T≤t≤3/2T内的分段函数表达式做了微调，使速度曲线更贴合实际运行需求.取参数值vinc=368.34 km/h，并且Tinitial=-160 log(1-200/vinc)，动车组运行的最高允许速度为350 km/h.具体表达式为

3.2 仿真结果分析

为了验证SM-LADRC 控制器追踪列车速度指令曲线的有效性和精确度，搭建图2 的Simulink 模型后进行仿真实验.将仿真时间设置为2 000 s，则速度指令曲线中的T=1 000 s.采样时间为默认值-1，表示系统自动采样.SM-LADRC 控制器中需赋值的控制参数共有8 个，分别如下：扩张观测器LESO 模块中b=0.009，w0=150，b0=0.009，SMC 控制律模块中c=5，k=0.1，w=0.1，σ=0.001，η=22.

在加载速度指令前，先在Vd模块中输入单位阶跃函数，用以验证控制器的响应速度.其跟踪结果如图3 所示.图3 中，0.052 s 后追踪误差渐进趋于0，与文献［7］相比，在反馈律中引入SMC 后的控制器响应速度更快.

图3 SM-LADRC 跟踪单位阶跃函数Fig.3 Unit step functions tracked based on SM-LADRC

然后加载式（9）到Vd模块中，用SM-LADRC控制器跟踪列车运行的速度曲线和位移曲线，得到的仿真结果如图4 所示.图4 中，无论是速度还是位移，实际跟踪曲线与指令曲线较吻合，表明SMLADRC 控制具有优越的跟踪性能.

图4 SM-LADRC 跟踪速度曲线和位移曲线Fig.4 Speed and displacement curves tracked based on SM-LADRC

为了进一步定量验证，分别求解出了速度和位移的跟踪误差值曲线，如图5 所示.图5 中，列车速度和位移的多数误差值均在平衡点附近上下波动，且总体来看存在很小的跟踪误差：SM-LADRC 跟踪的速度误差在±0.05 km/h 范围内，位移误差的最大波动点在±0.013 m 范围内，而文献［7］中使用ADRC 跟踪相同指令时的速度、位移误差分别为±0.15 km/h、0.05 m 范围内.

图5 跟踪速度和位移误差曲线Fig.5 Tracking speed and displacement error curves

对系统扰动x3的观测误差如图6 所示.参考实际运行经验，取外部扰动ψ=sin(0.77t)，阻力f(x)=-0.009wj，扰动观测误差e3=z3-x3.图6中，加入外部扰动前，即仅有x3=f(x)时，0 s 开始观测误差为0.034 2，随后误差值不断递减，0.22 s后在0 轴附近上下波动，但因为误差值特别小，图中横纵坐标轴的刻度相对误差值而言较大，故其变化过程体现得不太明显；加入外部干扰ψ后，即x3=f(x)+ψ时，0 s 开始对x3的观测误差同样为0.034 2，随后误差值逐渐递减，0.012 s 后系统补偿总扰动观测误差值在±0.001 6 范围内不断上下波动，这表明LESO 实现了对外部干扰的较精确观测和补偿.

图6 观测加入外部扰动前后的误差曲线Fig.6 Observing error curves before and after adding external disturbance

加入外部干扰后，速度、位移跟踪误差曲线如图7 所示.图7 中，加入外部干扰后的误差曲线与图5 相比变化很小，速度、位移曲线的跟踪误差仍分别保持在±0.05 km/h、±0.013 m 范围内，这说明SM-LADRC 的抗干扰能力较强.

图7 跟踪加入外部扰动后的速度误差曲线Fig.7 Tracking the velocity error curve after adding external disturbance

为更有说服力地表明所提控制方法在控制精度和抗干扰能力方面的优点，选择了与PID 控制、SMC 及LADRC 在同一条件下比较分析控制器的跟踪特性.各种控制方式的速度跟踪曲线对比仿真结果如图8 所示.图8 中，4 种控制器均可以大致跟踪理想曲线Vd，但SMC 的抖振现象明显，PID 控制效果也是差强人意；左侧局部放大图表明，SMLADRC 和LADRC 的速度跟踪曲线基本与理想曲线Vd重合，跟踪性能优于SMC 和PID 控制；再用右侧局部放大图比较SM-LADRC 和LADRC 的跟踪性能，SM-LADRC 跟踪曲线更贴合Vd，这表明SMLADRC 在跟踪精度方面更胜一筹.

图8 不同控制方法的速度跟踪曲线对比Fig.8 Comparison of velocity tracking curves using different control methods

不同控制方法的速度、位移跟踪误差曲线对比结果如图9 所示.图9 中，PID 控制和SMC 的速度跟踪误差分别在±2 km/h、±8 km/h 范围内，LADRC和SM-LADRC 的速度跟踪值都在零附近上下波动，所以这两个控制器在此性能控制方面表现更优；PID 控制和SMC、LADRC 的位移跟踪误差分别在±1 m、（-32 m，+12 m）、（-4 m，0 m）范围内，SM-LADRC 的位移跟踪误差基本呈水平线过零点，所以SM-LADRC 在此性能控制方面效果最好，这意味着列车追踪精度更高.