跳台滑雪助滑阶段计算流体动力学模拟及优化

2022-02-03唐伟棣杨宸灏曹峰锐

体育科学 2022年10期

唐伟棣，所向，杨宸灏，曹峰锐，伍勰，刘宇

（上海体育学院，上海 200438）

为了在跳台滑雪比赛中取得更高的分数，运动员都在寻求获得更远的飞行距离、更稳定的飞行姿态和更优雅的落地动作（如泰勒马克式落地，Telemark landing style）。而起跳阶段被认为是在跳台滑雪4个阶段（助滑、起跳、飞行、落地）中最重要的阶段（Elfmark et al.， 2021）。起跳阶段动作质量的高低决定了运动员的后续动作质量，即起跳阶段的动作完成情况决定了后续空中动作的弹道条件（ballistic conditions）（Virmavirta， 2016）。弹道条件包括抛射物的初始飞行高度、角动量、初速度大小及速度方向。一般来说，助滑阶段获得的速度越高，带来的抛射初速度也更高。而助滑速度的提升，意味着各国顶尖运动员矢志追求的飞行距离的提升（伍勰等， 2021； Schwameder，2008）。有研究表明，对于世界锦标赛级别的跳台滑雪运动员而言，助滑速度每提升1 km/h，理想情况下飞行距离将增加10 m左右（Virmavirta， 2017）。

助滑动作全过程位于助滑道上，根据国际雪联关于跳台滑雪跳台建设的规定，助滑道的设计由一段长直道、一段圆弧以及最后一段小直道组成。具体来说，出发端助滑道与水平面呈-35°，后接半径150 m左右的圆弧，最后的出发段为7 m左右的小直道，与水平面呈-10°。在这一过程中，运动员主要受到重力Fg、空气阻力FD、滑动摩擦力Ff（滑动摩擦力包含了雪板底部与冰面的摩擦力以及雪板侧面与滑道槽的摩擦力）、滑道支持力Fs等（图1）。运动员始终维持低位团身的姿势，躯干与滑道平面呈平行或接近平行的角度以减小身体的迎风面，从而降低助滑过程中受到的空气阻力。

图 1 运动员助滑过程受力分析示意图Figure 1. Analysis of the Force during the In-run Stage

为简化分析过程，将系统视为刚体，且滑动摩擦力及受到的重力（Fg=m·g，其中m为系统总质量，g即重力加速度，通常认为是一个常数）是与运动员助滑姿态无关的系数，则系统中的变量与运动员助滑姿态有关的是FD和FL。根据 Virmavirta（2016）使用 Aquila ski jumping simulator软件进行的模拟计算，可以认为系统受到的空气阻力和升力由以下公式表达：

其中：ρ为流体密度，在跳台滑雪运动中，这一指标与气压、湿度等因素相关，一般情况下认为是常数；v为系统速度大小，A为系统有效面积，CD为阻力系数，CL为升力系数。

助滑速度v在式中为唯一二次项，在输出值中权重最大，即助滑速度是影响系统受到的空气阻力及升力的主要因素，并且v2与系统受到的空气阻力及升力成正比关系。除此之外，其余变量（如CD和CL）则取决于系统气动外形及材料等，是一个相对稳定的值；余下与运动员身体姿态直接相关的因素为系统阻力面积A。在有关空气阻力的研究中，有效面积A指的是系统在垂直于速度方向平面上投影面积（projected areas）。压低上半身至水平面等手段的目标就是为了减小系统CD×A的值。

早在2006年都灵冬奥会上，Virmavirta等（2009）就通过影像分析的方法得出结论，认为助滑速度是影响飞行距离的最重要因素，但如何优化助滑姿态以同时满足运动员起跳发力条件和减小系统迎风面积条件仍然是亟待解答的问题。举例来说，在助滑阶段，运动员的手臂和手掌位置有多种姿态选择，但是否有最佳位置尚不明确（Elfmark et al.， 2021）。因此，进一步研究助滑阶段姿态优化，以追求可能存在的最佳助滑动作对提高跳台滑雪成绩至关重要，而计算流体动力学（computational fluid dynamics，CFD）也被认为是提高对跳台滑雪认知的重要工具（胡齐等， 2018；Cao et al.，2022）。目前国际主流研究已经针对跳台滑雪的全程特别是飞行阶段进行了较多的建模分析和研究，但针对助滑阶段的相关研究多采用数值分析等方法，截至目前，鲜见应用CFD等模拟计算手段进行助滑阶段动作优化的专门研究成果。本研究为寻找可能存在的跳台滑雪助滑阶段最优化气动姿态，特别是躯干、大腿的攻角等高权重因子对系统整体气动特性的影响，建立了运动员/雪板多体系统的三维数字孪生模型，并将系统置于助滑阶段的模拟环境中进行CFD分析，获取不同助滑姿态的气动特性以及在助滑过程中受到的升力阻力影响情况；通过CFD模拟仿真及分析，整合了不同姿态角度下运动员数字孪生多体系统的最优化肢体角度并探索运动员的特定助滑姿态在不同速度下的空气动力学特征，使用空气动力学模型对助滑姿态进行量化分析，通过优化助滑动作，以期获得更好的起跳条件，最终帮助运动员达到更远的飞行距离。

1 研究对象与方法

1.1 研究对象

以跳台滑雪运动员人体与雪板、头盔等装备组成的多体系统为研究对象。建模体态特征参考2022年跳台滑雪集训队5名男子运动员量体数据（表1），加权平均后数字孪生模型体态特征数据信息见表2。

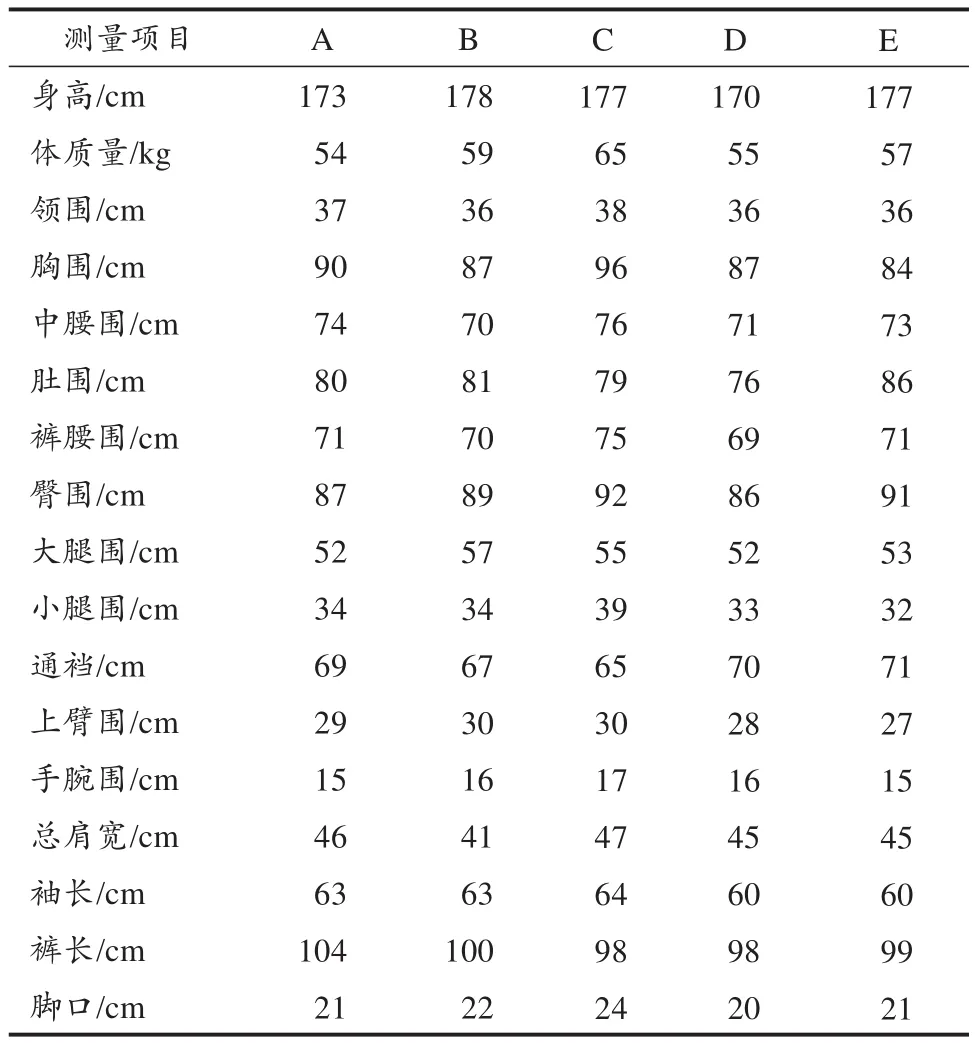
表 1 2022年跳台滑雪集训队男子运动员量体数据Table 1 The Athletes’ Physical Data of the Ski-Jumping Team in 2022

在助滑阶段，跳台滑雪运动员的运动学参数如图2所示，包括助滑速度v→、躯干攻角α、大腿攻角β、踝关节角γ、髋关节外展角ε，图中标示为角度的正方向。根据跳台滑雪助滑阶段的空气动力学相关研究结论，助滑末端速度取值 25 m/s（Elfmark et al.， 2021）。以该速度作为流场流体速度，探究不同姿态参数下是否存在最优助滑姿态。

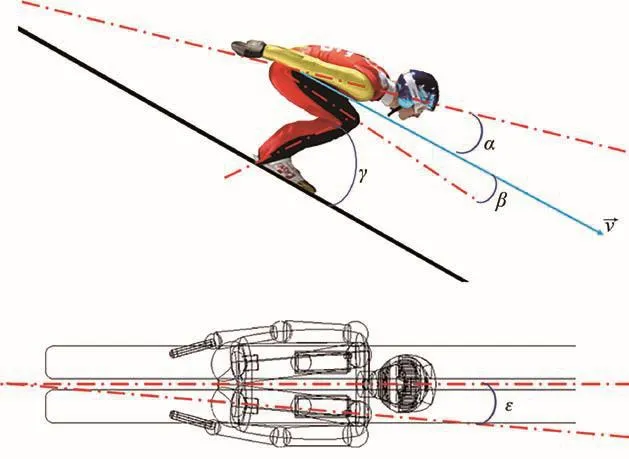
图 2 助滑阶段动作姿态参数Figure 2. Position Parameters in the In-run Stage

1.2 分析方法

1.2.1 湍流模型

k-ω湍流模型是目前在流体湍流研究中最为广泛使用的模型，其有效性也在不同领域的应用中得到验证（Chipongo et al.， 2020）。本研究使用剪应力传递k-ω模型（shear-stress transport k-ω model），该模型包含了基线kω模型的所有改进，并且被认为比标准k-ω模型和基线kω模型更为准确可靠，其表达式如下：

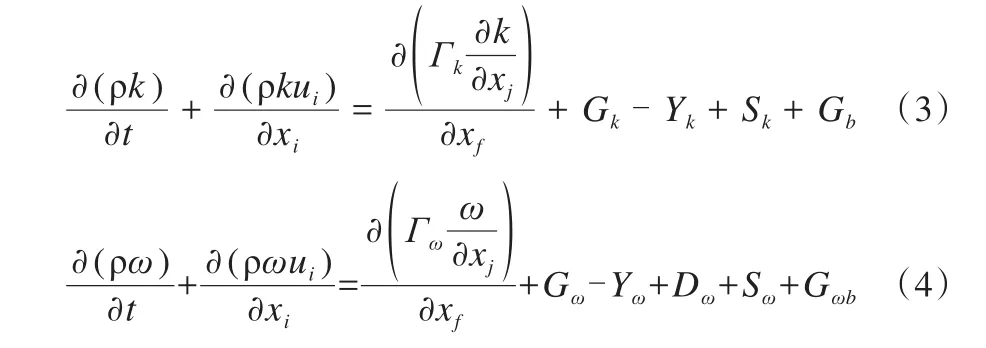
式中，t为系统时间，k为湍流平均比动能，ω为特定耗散率，ui为湍流平均速度向量，xi为位置向量，Γk和Γω是k和ω的有效扩散率，Gk和Gω为湍流动能生成项，Yk为Yω为对应的湍流动能耗散，Dω为交叉扩散项，Gb和Gωb为浮力引起的湍流，Sk和Sω为无量纲系数，主要描述流场中物体表面粗糙度。

表 2 数字孪生模型体态特征数据Table 2 Body Characteristic Data of Digital Twin Model

其中各系数由以下方程描述：

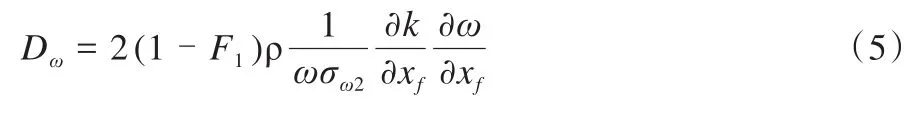
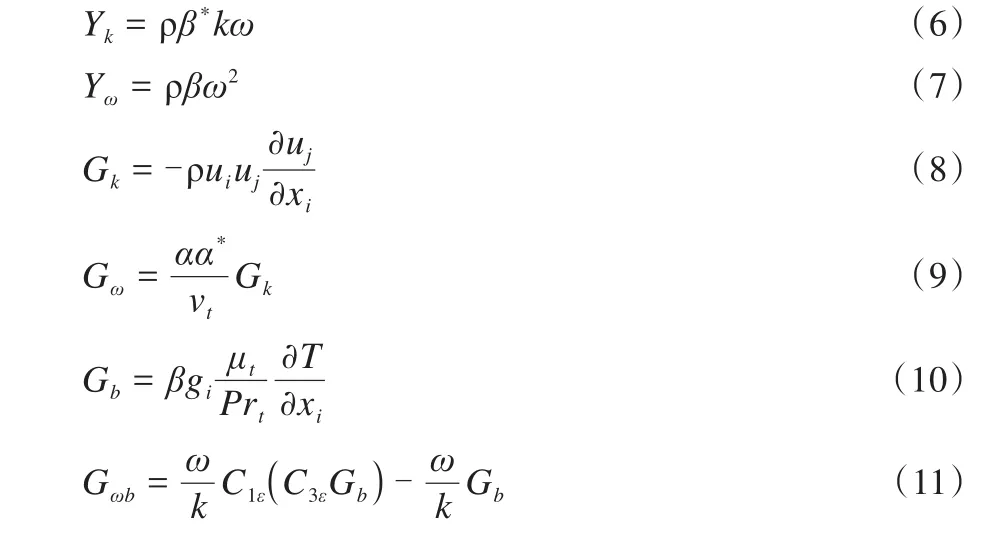
式中，P为系统静压，T为流体热力学温度，其余相关常数项取值为：σk1=2.0，σω1=2.0，σk2=1.0，σω2=1.168，βi1=0.075，βi2=0.082，C1ε=1.44 （Abrahamson， 2021；Wilcox， 2008）。根据以上方程，可以在获得跳台滑雪多体系统初始变量的情况下，模拟和计算整个多体系统在流场中的动能耗散和湍流动能耗散。

1.2.2 模型建立与网格划分

根据量体数据及助滑动作姿态参数，建立跳台滑雪运动员助滑阶段的三维数字孪生模型，对系统进行三维建模，并对在模型中设定关节锚点，实现对模型动作角度的精确控制，以满足研究中不同关节角度的动作要求。

根据相关空气动力学研究结论（Gardan et al.， 2017），本研究中流场阈（fluent domain）范围设定为6.0 m×5.0 m×13.8 m，运动员数字孪生模型位于流场压力入口面（inlet surface）中心法线上，距离入口面3.0 m（图3）。

图 3 流场域及多体模型示意图Figure 3. Schematic Diagram of Flow Field and Multi-body Model

根据跳台滑雪空气动力学气动特性模拟计算相关研究（胡齐等， 2020a），在跳台滑雪流场相关CFD建模计算中，网格最小分辨率以0.5 mm为佳，并且较为细致的网格单元分布在运动员数字孪生模型附近，以满足精确模拟模型周围流场细微变化情况，较大的网格则分布在远离模型的位置，在不影响计算结果的前提下，降低计算机流体模拟过程的时间消耗。在精细化模型的CFD模拟中，模型表面网格多面体数量为40层，增长率不大于1.1（Blocken et al.， 2019）。根据胡齐等（2020b）对跳台滑雪飞行气动特性的CFD分析，在1.0×107～2.5×107网格数量区间上，网格数量的变化对模型精确度并无显著影响，因此本研究采用精细化网格划分方法（图4），实际网格数量为23 628 556。

图 4 模型网格分布Figure 4. Model Grid Distribution

1.2.3 边界条件与流场搭建

在针对跳台滑雪助滑阶段的风洞计算与数值模拟研究中，Elfmark等（2021）发现躯干攻角及股骨与水平面夹角等姿态指标存在最优区间，但并没有从数值分析中找到最优组合。其中，躯干攻角α最优区间为0°～4°，大腿攻角β最优区间为22°～26°，踝关节角γ最优区间为45°～49°。根据区间划分，本研究将每个闭区间划分为3个离散值，将各种可能的姿态组合进行计算，具体速度及姿态参数如表3所示。

2 研究结果

2.1 结果总述

不同组别对应的姿态数据以及各组不同姿态角组合下的迎风面积［式（1）中CDA］、系统合升力、系统合阻力、升阻比（即系统在流体中受到的升力和阻力的比值）等信息详见表 4。以姿态 1组角度（α=0°，β=0°，γ=45°，ε=0°）为基准组（图5），观察系统在流场中的静压等线图，可以看到静压较高的区域首先出现在多体结构前端（即头盔部分），随着流体在多体系统表面流速逐渐加快，出现相对低压区，并在低压区后形成低压尾流。此后，流体从运动员的肩部和手臂等部分流过并逐渐加速，最终从多体系统分离，由于附面分离效应（原本紧贴物体表面流动的边界层流体脱离物体表面的现象，通常导致阻力上升，物体前后流体压强差上升等），尾部的静压出现了微量的增加。对躯干部分进行观察可以发现运动员躯干以及小腿的静压较小，换句话说，对系统受到的空气阻力贡献小。

表 3 数字孪生模型姿态动作参数列表Table 3 Position Parameter of Digital Twin Model

表 4 不同姿态角度工况下流体动力学仿真结果节选Table 4 Excerpts from Fluid Dynamics Simulation Results under Different Positions

Elmark等（2021）在助滑过程数值建模研究中发现，助滑道冰面与雪板的摩擦系数取μ=0.04能更好地描述系统力学过程。在助滑阶段，由于升力方向总是垂直于速度方向，如图1所示，升力FL增大则滑道支持力FS相应减小，为系统带来的直接收益则是Ff摩擦力减小。由于摩擦系数μ的取值已经确定，可知在不同姿态角组合下升力为系统带来的减阻收益小于系统总阻力（FS+FD）的2%，故后续对比实验中优先计算空气阻力FD对系统造成的影响。

2.2 髋关节外展角ε对系统受到阻力的影响

根据图6所示，纵坐标为累积空气阻力值，横坐标为计算平面与矢状面距离，最大值为运动员手臂外侧最远点与矢状面距离。由于运动员在助滑阶段动作是关于矢状面对称的，故后续讨论均以多体系统左半部分流场情况为目标。本研究中的系统流场形态主要由气流速度流线排布、对称面压力分布以及多体系统表面压力分布决定，诸如湍流云图等其他要素对系统的影响则由前述指标进行描述。

图 5 姿态1（基准组）系统静压等线图Figure 5. Contour Diagram of Static Pressure in Pose 1 （Basic Group）

图 6 不同组别髋关节外展角ε下系统累积空气阻力图Figure 6. The Cumulative Force of the System by the Angle ε in Different Groups

可以看到髋关节外展角以姿态4，也就是髋关节外展角度ε=-4°组所受到的空气阻力最大，观察此时系统流场形态对比，如图7～10所示：

图 7 姿态1髋关节外展角ε下系统迹线图Figure 7. Path Lines of Pose 1 with Angle ε

图 8 姿态2髋关节外展角ε下系统迹线图Figure 8. Path Lines of Pose 2 with Angle ε

可以看到流场迹线图中髋膝踝连线附近的流场迹线受髋关节外展角影响，相较于姿态1的迹线，姿态2在对应位置的浅色迹线更多，这表明相较于ε=0°的情况，正向的髋关节外展角度将为系统带来负面的空气阻力收益。而对于髋关节角度内收的情况，相较于姿态2的外展而言，姿态3髋膝踝连线附近流场迹线与姿态1相似，并无明显差异。从累积空气阻力的计算结果来看，姿态3受到的空气阻力大于姿态2，小于姿态1，但数值十分相近。为验证髋关节外展负角度的提升是否与阻力大小成反比，实验组中增加了姿态4组，髋关节外展角度定为ε=-4°。通过迹线图，可以看到膝关节附近浅色迹线明显多于其他3组，表明运动员腿部髋关节以更大角度内收后将导致多体系统空气动力学性能较大幅度下降，反而产生了更大的空气阻力。

图 9 姿态3髋关节外展角ε下系统迹线图Figure 9. Path Lines of Pose 3 with Angle ε

图 10 姿态4髋关节外展角ε下系统迹线图Figure 10. Path Lines of Pose 4 with Angle ε

2.3 踝关节角γ对系统受到阻力的影响

通过累积阻力图发现（图11），踝关节角的增大将为系统带来较多的空气动力学优化损失，在相同情况下将导致更高的空气阻力。

He invited me to dinner where we talked longer and deeper.

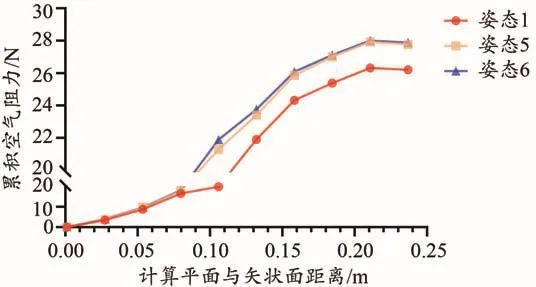
图 11 不同组别γ角度下系统累积空气阻力图Figure 11. The Cumulative Force of the System by the Angle γ in Different Groups

可以看到，图12与图13中多体系统的下半部分存在较多的浅色迹线（与图7相比），这表明踝关节角的提升将直接干扰气流在多体系统下半部分的气动表现。由于踝关节角的增大，系统的正面迎风面积相应增大，带来相应的空气阻力增大，这与空气动力学的原则是相符合的。较高的踝关节角度不但劣化了多体系统下半部分的气动性能，更直接的影响是造成了运动员脚部与雪板连接处进一步的流体速度损失，相较于姿态1同一位置，姿态5与姿态6在该位置上的迹线以相对低速的蓝、绿色迹线为主。

图 12 姿态5踝关节角γ下系统迹线图Figure 12. Path Lines of Pose 5 with Angle γ

图 13 姿态6踝关节角γ下系统迹线图Figure 13. Path Lines of Pose 6 with Angle γ

2.4 大腿攻角β对系统受到阻力的影响

从图14中可以看到，对于大腿攻角β来说，存在局部最优解β=24°，此时系统受到的空气阻力最小。

观察姿态 1、姿态7（图15）、姿态8（图16）迹线图，可以看到在大腿攻角β从22°向26°增大的过程中，系统迹线变化趋势并不是线性的。单独观察髋膝踝连线右侧迹线，可以发现随着大腿攻角的增大，迹线群色调逐渐升高——这表明多体系统下肢部分对流体的阻滞作用减小了，这导致了更多的高速流体分子绕过多体系统下肢部分而不是与系统发生能量交换，从而产生空气阻力。但整体观察多体系统右侧迹线，可以看到随着躯干部分由于大腿攻角提升而升高，系统整体气动表现反而出现了下降，最终导致大腿攻角只在β=24°附近存在局部最优解，过高或者过低的攻角都导致系统表现出了更大的空气阻力。

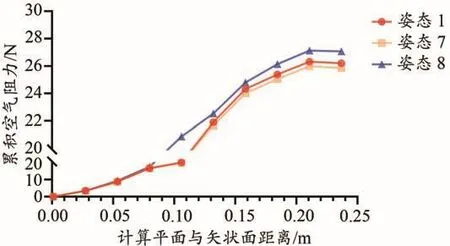
图 14 不同组别β角度下系统累积空气阻力图Figure 14. The Cumulative Force of the System by the Angle β in Different Groups

图 15 姿态7大腿攻角β下系统迹线图Figure 15. Path Lines of Pose 7 with Angle β

图 16 姿态8大腿攻角β下系统迹线图Figure 16. Path Lines of Pose 8 with Angle β

2.5 躯干攻角α对系统受到阻力的影响

从图17中可以看到，对于躯干攻角α，存在局部最优解为α=2°，此时系统累积空气阻力最终值略小于基准组，相较于α=4°则减小了5.5%。

不难发现，与姿态9（图18）相比，姿态10（图19）攻角迹线中，多体系统背部迹线绿色部分更多，其流体分子流速在相同位置显著低于姿态1与姿态9。这表明随着躯干攻角的升高，多体系统中最大的截面部分躯干体对系统整体的空气动力学表现造成的影响显著大于其他部分（如下肢等）。由于躯干攻角的升高，多体系统在大腿与躯干之间的迹线出现了更多蓝色和绿色，这表明躯干攻角产生的影响在整个系统中均较为重要，不仅仅体现在局部。

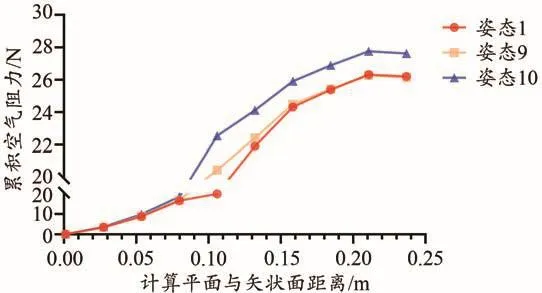
图 17 不同组别α角度下系统累积空气阻力图Figure 17. The Cumulative Force of the System by the Angle α in Different Groups

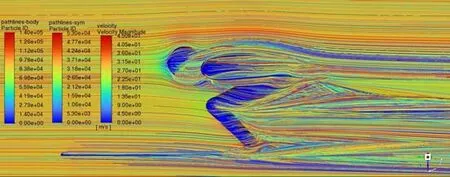
图 18 姿态9躯干攻角α下系统迹线图Figure 18. Path Lines of Pose 9 with Angle α

图 19 姿态10躯干攻角α下系统迹线图Figure 19. Path Lines of Pose 10 with Angle α

3 优化结果与讨论

3.1 优化结果

根据流场模拟计算，目前的姿态角最优解组合为躯干攻角 α=2°，大腿攻角 β=24°，踝关节角 γ=45°，髋关节外展角ε=-2°。将最优解组合命名为优化组，观察此时姿态1与优化组的累积空气阻力对比图（图20），可以看到优化组多体系统在整个流场中的累积空气阻力值都得到了一定程度的下降，空气动力学性能表现得到优化。最终的累积空气阻力相较于默认的基准组减小了4.6%，相较于模拟中阻力最大的姿态4则减小了13.2%。

观察优化组速度级数矢量图（图21）可发现，大部分低速气流主要集中在头盔顶、脚尖等尖端位置，速度方向与顶面法线相垂直。高速气流附面主要是背向流体来流方向的曲面，这表明相应的区域在多体系统的气动表现中影响较小，流体在经过这些面后速度基本不发生损失，对系统整体形成的空气阻力也较小。

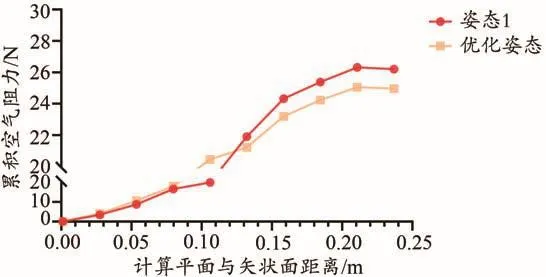
图 20 姿态1与优化组系统累积空气阻力对比图Figure 20. The Cumulative Force between Pose 1 and Optimized Pose

图 21 优化组速度级数矢量图Figure 21. Vector Graph of Velocity Magnitude of Pose Optimized Pose

3.2 助滑阶段躯干姿态讨论

在针对躯干姿态进行调整的模拟计算中（图7，图18，图19），可以发现躯干攻角的变化导致了系统空气阻力的较大变化：躯干攻角每变化1°，系统累积空气阻力变化量为5.7%；与此相对的是踝关节角每变化1°，系统累积空气阻力变化量约为0.5%。不难发现，躯干攻角因为截面积较大，其细微变化在整个多体系统中影响较大，在躯干攻角α=0°附近，由于躯干攻角增大而增大的多体系统投影面积增速较低，带来的阻力增加量也较少，随着躯干攻角的增加，相同的攻角提升将带来更多的投影面积增加，也就意味着相较之前更大的空气阻力。

根据计算结果，不难发现姿态1与姿态9在累积空气阻力图上表现十分接近，这主要是由于躯干整体长径比（即物体长度与其截面积直径的比值）较低，同样长度情况下，长径比越低的物体，在流体流速方向垂直面上的投影面积越小，根据式（2），易知这类多面体对来流的角度变化相对不敏感。

另一个需要注意的现象是，本研究中模拟结果以躯干攻角α=2°为最优，是以较小的投影面积增加为代价，改良了系统整体的气动特性，特别使得前胸附近的流体迹线得到优化（图18），整体减少了躯干部分对流体分子的减速效果。在躯干攻角从α=2°向α=4°增大的过程中，系统投影面积急剧增加，与此同时，攻角角度增加为多体系统胸前流体的迹线优化带来的收益并未抵消投影面积增加带来的阻力提高（图19中姿态10较姿态9累积空气阻力增加9.4%）。

3.3 助滑阶段下肢姿态讨论

综合对踝关节角和髋关节外展角2个姿态变量的模拟计算结果（图6～13）发现，下肢部分对多体系统的空气动力学特性影响相对较小。如前文所述，由于下肢部分相对躯干而言截面积较小，且大腿等结构的中轴线与水平轴夹角远大于躯干攻角，导致下肢部分角度的改变对系统在迎风面积上的贡献较小。

除了对迎风面积的改变，下肢角度在多体系统空气动力学特性上的影响体现在多体系统与地面（助滑道）距离的改变上。较小的踝关节角除了带来更小的空气阻力投影面积，对多体系统胸部等区域的流场形态产生了正面影响，进一步减小了流体在这些区域的速度和能量损失。这一影响的机理可以通过针对地面效应的模拟计算或者风洞实验来进行进一步验证。Rozhdestvensky（2006）在关于极端地面效应（extreme ground effect，EGE）的论述中认为，地面效应在运动物体与地面距离小于主翼弦的10%时便会出现。具体到本研究中，膝-踝连线在某种程度上满足EGE效应出现的条件，这有可能是导致下肢角度姿态变化后引起升力较大变化量的重要因素。要对该现象进行严谨的验证，可以在后续相关研究中对不同姿态角下的多体系统下肢部分进行空中和近地的升力验证对比实验。