发动机热力循环参数对流路参数的影响
2022-02-03李瑞军计自飞
李瑞军,计自飞
(中国航发沈阳发动机研究所,沈阳 110015)
经过几十年的发展,航空发动机的技术水平有了很大的提高,主要表现在耗油率降低、单位推力增加、寿命和费用降低、安全性增强等方面[1-2]。发动机性能的提升很大程度上得益于总增压比、涡轮前温度等热力循环参数的持续提高[3]。
热力循环参数分析是航空发动机概念设计阶段总体性能设计的重要环节,高的热力循环参数虽然有利于提升发动机的性能,但需要各方面的技术进步作为支撑[4],因为高的热力循环参数会导致发动机部件气动负荷、机械应力负荷和热应力负荷增加,进而影响部件效率的实现,同时也可能会导致发动机质量的增加,未必会达到预期的性能结果。因此,在发动机概念设计阶段,开展发动机热力循环参数分析时,综合考虑发动机流路尺寸、部件气动负荷系数、涡轮AN2值、旋转部件切线速度等因素,对获得综合性能较佳的总体方案具有十分重要的工程价值。
张少峰等[5]以涡轴发动机为研究对象,开展了涡轴发动机性能与流路尺寸及质量之间的耦合评估方法研究;郑恒斌等[6]以大涵道比涡扇发动机为研究对象,基于ISIGHT商用软件,建立了大涵道比涡扇发动机热力循环参数和几何流路尺寸之间的优化模型,开展了大涵道比热力循环参数对发动机流路影响的研究。从公开的材料来看,研究对象主要以涡轴和大涵道比涡扇发动机为主,所开展的研究工作均取得了一定进展,提高了航空发动机热力循环参数分析的全面性和系统性。但是针对军用小涵道比涡扇发动机还未见相关研究工作,并且文献研究更偏向方法的介绍,工程实用性有待进一步提高。
本文以总增压比、涡轮前温度、涵道比等热力循环参数为自变量,以叶轮机各部件流路尺寸、平均负荷系数、涡轮AN2值等为目标变量,建立了航空发动机热力循环参数与流路尺寸之间的迭代关系模型。基于该迭代模型,假设一个基准方案,研究总增压比、涡轮前温度和涵道比等单一自变量变化时对流路尺寸、涡轮AN2值等目标变量的影响。利用该计算模型,可实现在航空发动机概念设计阶段,考虑部件能力水平和约束条件下的发动机热力循环参数优化选取,对航空发动机工程设计具有重要参考意义。
1 研究对象及内涵
本文研究的发动机构型为配装战斗机用的双转子加力式涡扇发动机,截面代号如图1所示。与涡轴发动机相比,循环参数增加了涵道比;与大涵道比涡扇发动机相比,风扇和压气机之间没有增压级,低压部件流路匹配关系有差异。

图1 双转子加力式涡扇发动机
研究的热力循环参数包括总增压比πΣ、涡轮前温度T4和涵道比BPR;流路尺寸为典型特征截面的径向尺寸,主要包括风扇进口外径d2、压气机进口平均直径d25、压气机出口平均直径d3、高压涡轮出口平均直径d44和低压涡轮出口平均直径d5;代表风扇、压气机和涡轮气动性能水平的平均负荷系数,以平均到各叶轮机部件中径位置的平均切线速度作为评估对象;代表机械应力水平的参数主要包括高、低压转子转速n1和n2,以及高、低压涡轮AN2值。
2 计算模型和方法
2.1 发动机性能计算模型
根据文献[7-9]建立了双转子涡扇发动机热力循环参数计算模型,发动机部件包括进气道、风扇、压气机、主燃烧室、高压涡轮和低压涡轮等[10]。给定设计点飞行和大气条件,选定发动机循环参数和部件效率及流道损失系数等,进行发动机热力循环计算,获得发动机重要特征截面的气动性能参数和功率需求等,为流路尺寸评估提供气动输入条件。
研究过程中,部件效率、流道损失系数等参数保持常数不变,自变量参数为风扇压比πF、压气机压比πC、涡轮前温度T4和涵道比BPR,目标参数为各个截面的流量、总压和总温,如式(1)、(2)所示
Y1=[Qx,Px,Tx]
(1)
Y1=f(πF,πC,T4,BPR)
(2)
其中:Y1为性能目标变量;Q、P、Y和T分别为流量、总压和总温,x代表截面代号。
2.2 流路参数计算模型
根据文献[11-14]建立发动机流路参数计算模型,主要包括风扇、压气机、高压涡轮和低压涡轮4个部件。
在流路计算过程中,首先建立压气机和涡轮功率平衡方程,用压气机进口中径截面平均负荷系数表征压气机单位功率为[15]

(3)
其中:φHPC为压气机平均负荷系数;ZHPC为压气机级数;U25为压气机进口中径截面上的平均切线速度。
用高压涡轮出口中径截面平均负荷系数表征高压涡轮单位功率为

(4)
其中:μHPT为高压涡轮平均负荷系数;ZHPT为高压涡轮级数;U44为高压涡轮出口中径截面上的平均切线速度。
压气机功率等于涡轮功率,可得出
Q25∇HHPC=Q41∇HHPTηmHηHPT
(5)
其中:Q25为压气机进口空气流量;Q41为进入高压涡轮参与做功的燃气流量;ηmH为高压轴机械效率;ηHPT为高压涡轮等熵效率。
将式(3)和(4)代入式(5),并且根据叶轮机原理可知,同一根轴上的压气机和涡轮切线速度之比等于径向尺寸之比,可得出压气机和高压涡轮的几何尺寸匹配关系为
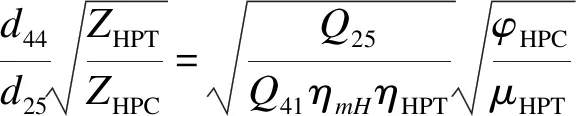
(6)
其中:d25、d44分别表示压气机进口中径截面平均直径、高压涡轮出口中径截面平均直径。
同样原理,可得出风扇和低压涡轮的几何尺寸匹配关系为
(7)
其中:d2为风扇进口截面平均直径;d5为低压涡轮出口截面平均直径;Q2为风扇进口空气流量;Q45为进入低压涡轮参与做功的燃气流量;ηmL为低压轴机械效率;ηLPT为低压涡轮等熵效率;φFAN为风扇平均负荷系数;μLPT为低压涡轮平均负荷系数。
流路计算过程中,各特征截面的面积S为
(8)
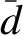
(9)
(10)
(11)
其中:dt和dh分别为特征截面外径和内径。
在流路尺寸计算模型中,转速是压气机和涡轮匹配设计时最重要的关联参数,提高转速有利于减少压气机和涡轮级数。转速的提高受到涡轮强度的约束,主要由涡轮工作叶片决定,预估涡轮工作叶片应力时,通常由离心力引起的拉伸应力表征,拉伸应力参数ε定义为[11]
(12)
其中:σp为叶根截面离心力引起的拉伸应力;ρ为叶片材料密度;Kφ为叶片形状无因次系数。
根据叶片机原理,拉伸应力参数ε与涡轮出口面积Se和转速n的平方有关,因此在发动机概念设计阶段,可用涡轮AN2值表征涡轮机械应力水平[11],如式(13)所示
ε=πSen2
(13)
2.3 热力循环参数与流路参数迭代计算方法
在性能计算模型和流路参数计算模型基础上,建立热力循环参数与流路参数之间的迭代模型,热力循环参数πΣ、T4、BPR为函数自变量,Y2、Y3、Y4分别代表3个函数因变量的数据集,分别为尺寸、负荷系数和AN2,如式(14)~(16)所示
Y2=[dx,dxt,dxh]=f(πΣ,T4,BPR)
(14)
Y3=[φFan,φHPC,μHPT,μLPT]=f(πΣ,T4,BPR)
(15)
(16)
计算分析流程如图2所示,详细描述如下:
第一步:根据飞机对发动机推力、耗油率、尺寸等要求作为输入参数,选取一组满足总体设计要求的热力循环参数。

图2 热力循环参数与流路尺寸迭代计算分析流程图
第二步:以热力循环参数计算输出的各截面气动参数、给定的马赫数和各叶轮机流路形状等作为输入,开展发动机流路参数计算,确保高、低压涡轮AN2值在机械应力限制范围之内;同时检查高压压气机、高压涡轮以及风扇与低压涡轮之间的流路尺寸匹配是否合理。如果不合理,则需返回再调整热力循环参数;如仍不合理,再返回调整热力循环参数,直到各流路尺寸匹配合理为止。
第三步:在流路尺寸匹配合理的情况下,开展风扇、压气机和高、低压涡轮平均气动负荷系数计算。如果各部件气动负荷系数超出经验限制值,则需返回调整流路尺寸计算输入参数;如仍超出,再返回调整热力循环参数,直到调整至限制范围内为止。
第四步:在部件气动负荷系数合理情况下,检查气动负荷系数与效率的匹配度,并开展发动机整机性能验算,检查最终输出的推力、耗油率等性能参数是否满足最初的设计要求,如果不满足,则需调整设计要求;如果满足,则本项工作结束,输出计算结果即可。
以上工作需经过多轮反复迭代,最终输出一套既满足设计要求,技术风险又可控的热力循环参数方案。
3 算例与分析
以某型发动机为基准方案,在该方案基础上将热力循环参数作为自变量X,研究其对发动机流路尺寸、涡轮AN2值等目标变量Y的影响。
3.1 总增压比对流路参数影响分析
研究总增压比对流路参数影响时,各截面马赫数和部件级数保持不变,同时假定风扇、压气机和高、低压涡轮气动平均负荷系数保持在合理的范围之内不变。由于研究的各方案进口流量一致,因此对风扇尺寸无影响。随着增压比的增加,压气机进出口尺寸、高、低压涡轮出口尺寸变化如图3所示,由图3可得出如下结论:
(1)随着总增压比的增加,压气机进口尺寸无影响,压气机出口平均直径稍有增加,但变化不是特别明显。总增压比的增加通过提升压气机压比实现,因此对压气机进口无影响,而压气机出口随着压比增加,出口环面面积减小,叶片变短,导致出口平均直径稍有增加。
(2)随着总增压比增加,高压涡轮和低压涡轮出口平均直径减小,主要由高、低压涡轮出口叶栅环面面积减小所导致。
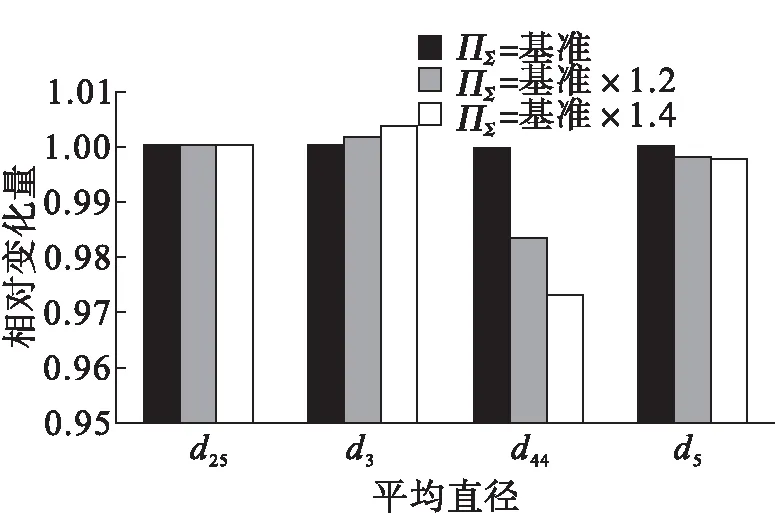
图3 总增压比变化对流路尺寸影响
总增压比增加对高、低压转子转速和涡轮AN2值影响如图4所示,由图4可得出结论:
(1)由于低压转速n1由风扇尺寸和切线速度决定,通过压气机增加总增压比,对风扇尺寸和平均负荷无影响,因此n1无变化;随着增压比的增加,为保持高压压气机和涡轮气动平均负荷系数不变,n2随着增压比增加持续增加。
(2)随着增压比的增加,低压涡轮AN2值减小,而高压涡轮AN2值增加,且增加的幅度与转速基本相当。原因是n1不变,低压涡轮出口面积减小,因此低压涡轮AN2值减小,而高压涡轮出口面积减小的幅度小于转速增加的幅度,因此高压涡轮AN2值增加。

图4 总增压比变化对转速和AN2值影响
3.2 涡轮前温度对流路参数影响分析
研究涡轮前温度T4对流路参数的影响时,假设条件与增压比分析一致,各截面马赫数和部件级数同样保持不变。同时假定风扇、压气机和高、低压涡轮气动平均负荷系数保持不变,涡轮前温度相比基准方案增加50 K和100 K时对发动机流路尺寸和高、低压转速及高、低涡轮AN2值的影响如图5和图6所示,由图5、6得出如下结论:
(1)随着涡轮前温度T4的增加,对压气机尺寸无影响,高压涡轮出口平均直径增加,低压涡轮出口平均直径减小,但总体影响量很小,几乎可忽略。造成这种小差异的原因主要由不同温度条件下的燃气气体指数不同所致。
(2)随着涡轮前温度T4的增加,对高、低压转子转速几乎无影响,对降低高、低压涡轮AN2值有利。原因是在总增压比不变的情况下,随着T4温度的增加,高、低压涡轮出口环面面积均减小,高、低压转速不变的情况下,高、低压涡轮AN2值均减小。
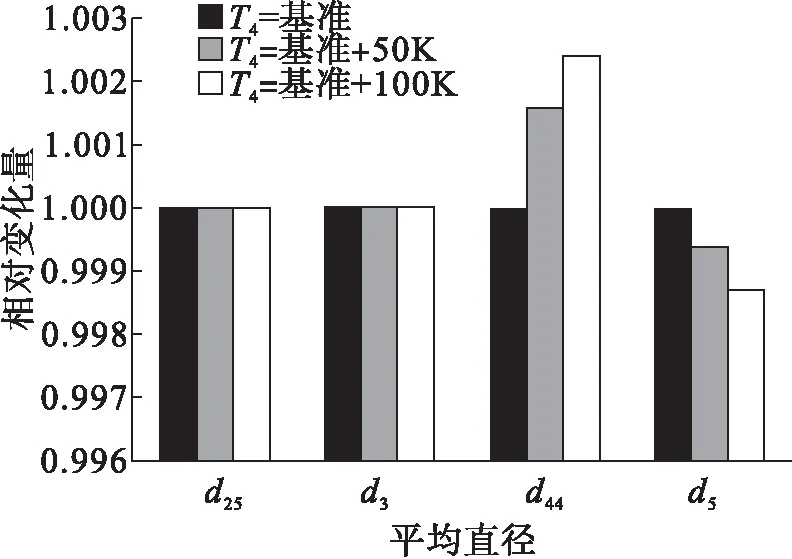
图5 涡轮前温度变化对流路尺寸的影响

图6 涡轮前温度变化对转速和AN2值的影响
3.3 涵道比对流路参数影响分析
研究涵道比影响的假设条件与总增压比和涡轮前温度的假设条件完全一致,涵道比对发动机流路尺寸和高、低压转速及涡轮AN2值的影响如图7和图8所示,由图7、8可得出如下结论:
(1)随着涵道比的增加,压气机平均直径和高压涡轮出口平均直径减小,低压涡轮出口平均直径增加。原因是随着涵道比的增加,核心机进口流量减小,压气机和涡轮直径必然减小;但是随着涵道比的增加,低压涡轮发出的单位功率增加,为保持同样低压涡轮平均负荷系数,只能通过抬高低压涡轮的流道尺寸实现。
(2)随着涵道比的增加,低压转速和高压涡轮AN2值基本保持不变,高压转速增加,低压涡轮AN2值减小。原因是随着涵道比的增加,风扇进口流量并没有变化,因此风扇进口尺寸不变,风扇进口切线速度不变的情况下,低压转子转速自然没有变化;由于涵道比的增加没有影响高压压气机和高压涡轮的单位功率平衡关系,因此对高压涡轮AN2值没有影响;在高压涡轮保持同等切线速度情况下,由于尺寸减小,高压转子转速必然增加;对于低压涡轮AN2值来说,低压转速不变,但是随着涵道比的增加,低压涡轮出口面积减小,因此低压涡轮出口AN2值减小。

图7 涵道比变化对流路尺寸的影响
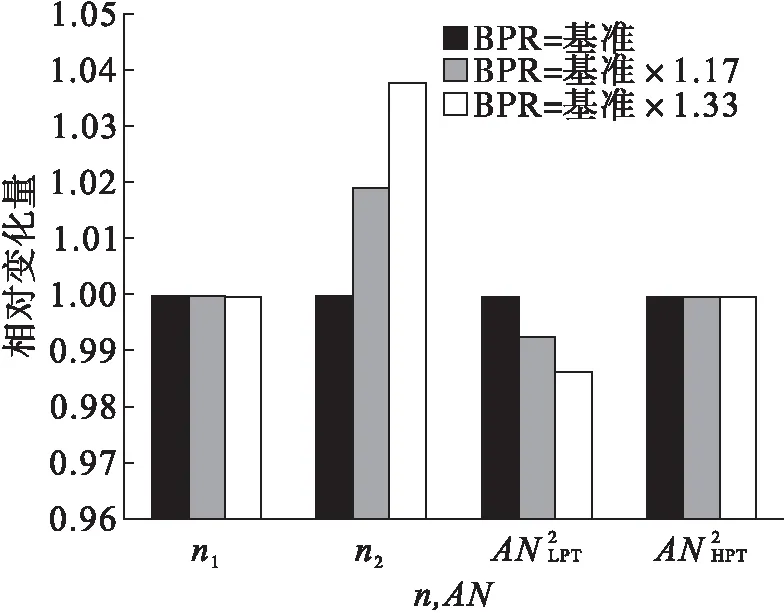
图8 涵道比变化对转速和AN2值的影响
3.4 发动机整机性能验算
当完成各部件气动负荷系数计算后,需验算和检查该负荷系数下的部件性能是否能够满足整机性能要求。下面以低压涡轮为例,首先根据计算得到的低压涡轮平均负荷系数μLPT和流量系数Urc.LPT,从图9所示的涡轮Smith图[6]中查得低压涡轮效率,然后将该效率与热力循环参数分析时输入的低压涡轮效率进行对比,根据对比偏差评价是否满足整机性能要求。其他部件可采用类似的方法依次验算,如果评估某一单个部件不满足要求,但综合评估推力和耗油率满足整机性能要求也是可行的,最终获得一套合理可行的热力循环参数方案。
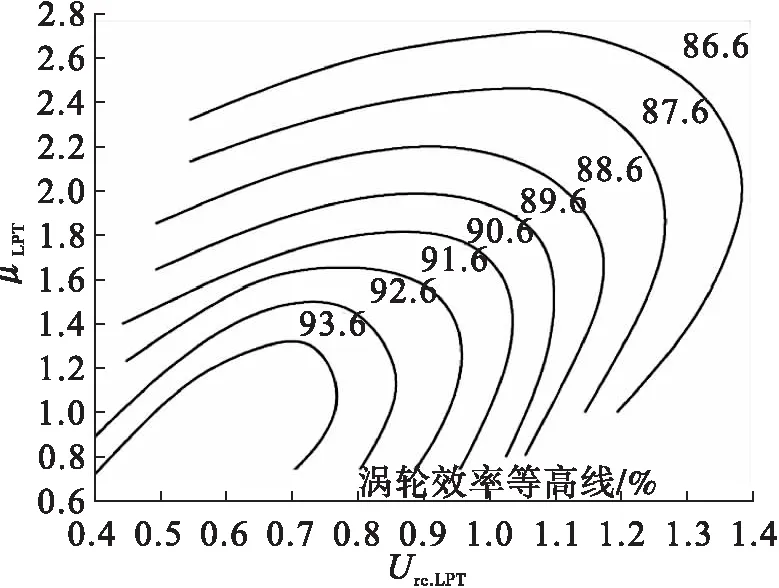
图9 涡轮Smith图[6]
4 结论
为分析发动机热力循环参数对流路参数的影响,本文建立了发动机热力循环参数计算模型和流路参数计算模型,以及它们之间的迭代关系模型,通过模型完成算例计算,得出主要结论如下:
(1)热力循环参数对流路参数有很大的影响,在总增压比增加的情况下,一定会带来叶轮机机械应力和气动设计难度的增加,需折中平衡机械结构和气动设计之间的难度。
(2)涡轮前温度的增加有利于高、低压涡轮AN2值降低,可有效地降低叶片结构拉伸应力设计难度,但需在热应力和拉伸引力之间平衡。
(3)涵道比影响高、低压之间的功率分配,增加涵道比有利于减小核心机部件径向尺寸和中间状态耗油率,但同时会导致发动机推力降低,需平衡好推力、尺寸和耗油率之间的关系。
