基于改进K调和均值聚类的跳频信号分选方法

尚佳栋，张文婧，杨春景

(中国航天科工集团第二研究院 北京遥感设备研究所，北京 100854)

跳频通信具有良好的组网能力，通过组网可以达到扩展通信覆盖范围和增大通信容量的目的，同时能够增强通信系统的存活能力。目前组网通信已经成为跳频通信系统具有的基本功能[1]，因此对跳频通信网内各电台的信号进行分选成为跳频通信侦察中的一项重要任务[2]。在实际应用中，跳频电台多采用组网的方式进行通信和数据信息传输，提高电台的通信容量，同时提高整个系统的抗干扰能力。在跳频网络中多个电台同时发送数据，侦察接收机的截获信号即为多个跳频信号的时域混叠信号。时频分析方法能够对混叠信号进行处理，通过时频分析得到每跳信号的参数估计值。然而仅利用每跳的参数值，无法得到信号完整的跳频图案，也就无法对网络内每个跳频电台进行盲接收和信息提取。因此，为完成对跳频信号的侦察，需要将相互混叠的多个跳频信号分离，分别进行单独处理。此外，利用跳频信号的分选结果可以获取敌方电台的数量和分布的大致范围，利用此信息可以进一步得到敌方的通信装备水平、作战意图、布防阵容以及指挥隶属关系等重要战略情报。

根据分选时是否需要信号参数信息，分选方法分为非盲的分选方法和盲分选方法两类。非盲的分选方法以参数估计结果为基础，利用跳频电台在功率、到达方向(Direction of Arrival,DOA)、到达时间(跳时)、跳频周期以及载波频率等特征的不同，采用聚类分析算法对信号进行分选；盲分选方法是在盲源分离理论的基础上发展而来，利用信号之间的统计独立特性，在信号参数未知的条件下实现信号的有效分离。

考虑到跳频信号具有非平稳特性，目前部分研究采用时频分析相关算法估计跳频信号参数。例如，文献[3-5]在短时傅里叶变换的基础上，设定合适的阈值辨别信号并提取跳频信号的时频脊线估计信号参数，采用 Gabor 变换、小波变换、谱图、魏格纳威尔分布及其改进算法处理跳频信号，提取时频脊线估计跳频参数。各类时频分析方法优缺点各有不同，但提取时频脊线的方法依旧仅适用于单跳频信号的参数估计。文献[6]提出一种基于跳频中心时刻的跳频信号参数估计方法，解决多网台混合跳频信号参数估计的问题。首先通过设定门限和聚类算法提取每跳信号的中心时刻，再利用脉冲重复间隔变换得到跳频周期。文献[7]将时频分析得到的二维矩阵转化为灰度图像，结合图像处理领域中的经典算法分析跳频信号并估计相关参数，该方法给跳频信号参数估计领域带来新的启示。根据以上思路，文献[8]利用时频图的纹理特征将有用信号和底噪分离，并通过聚类去除各类干扰，通过图像处理中的开闭运算处理跳频信号时频图像，将像素点位置与信号参数对应得到估计结果。

在非盲的跳频信号分选方法研究方面，文献[9]提出一种基于优化K-Means算法的跳频信号分选方法，将信号的载频、跳周期、跳时、功率以及DOA的估计值作为特征矢量参数，通过搜索参数统计直方图的峰值预估计聚类数，然后根据峰值的中心点位置对信号进行聚类分选。与传统的聚类分选方法相比，该方法有效减少了迭代次数，并且能够避免聚类过程陷入局部最小。然而，优化K-Means分选方法没有考虑聚类数估计误差对聚类结果的影响，在参数估计方差较大时会出现聚类错误。文献[10]分别对优化K-Means分选方法进行改进，通过聚类合并消除虚假的类，降低了聚类数估计值对聚类结果的影响，提高了对跳频信号的正确分选概率。在盲分选方法研究方面，文献[11]在阵列天线接收的基础上，分别采用独立分量分析(Independent Component Analysis,ICA)算法和联合特征矩阵对角化(Joint Approximate Diagonalization of Eigenmatrixex,JADE)算法估计跳频信号的混合矩阵，通过矩阵求逆完成了对跳频信号的盲分选。由于盲分选方法假设各跳频电台信号的相互独立，而没有利用信号自身的特征参数信息，因此其分选性能弱于基于聚类的分选方法。此外，参数估计是跳频信号侦察中不可缺少的环节，因此基于聚类分析的跳频分选方法在工程应用方面具有更好的潜能。

新型跳频信号组网通信的机理和传统的跳频信号完全相同，只要能够获得足够精度的参数估计值，采用相同分选方法即可实现对新型跳频信号的分选，但目前专门针对直接序列扩频(Direct Sequence Spread Spectrum,即DS)通信/跳频(Frequency Hopping,即FH)信号和差分跳频(Differential Frequency Hopping,即DFH)信号分选方法的研究较少。文献[12]提出采用JADE算法对DFH信号进行盲分离。

针对在参数估计误差较大条件下，跳频分选存在的问题，本文同时从优化聚类中心和确定最优聚类数的角度出发，将直方图统计和有效性指标相结合对现有的KHM聚类算法进行改进，提高聚类分选正确的概率，从而实现对跳频信号的有效分选。

1 采用聚类算法的跳频信号分选原理

跳频信号聚类分选方法的基本原理结构如图1所示。在该结构中不仅包含了信号的分选内容，还包括了信号检测和参数估计的内容，即在跳频通信的侦察研究中信号检测、参数估计和信号分选三者缺一不可，它们相互协作构成一个完整的跳频信号侦察流程。

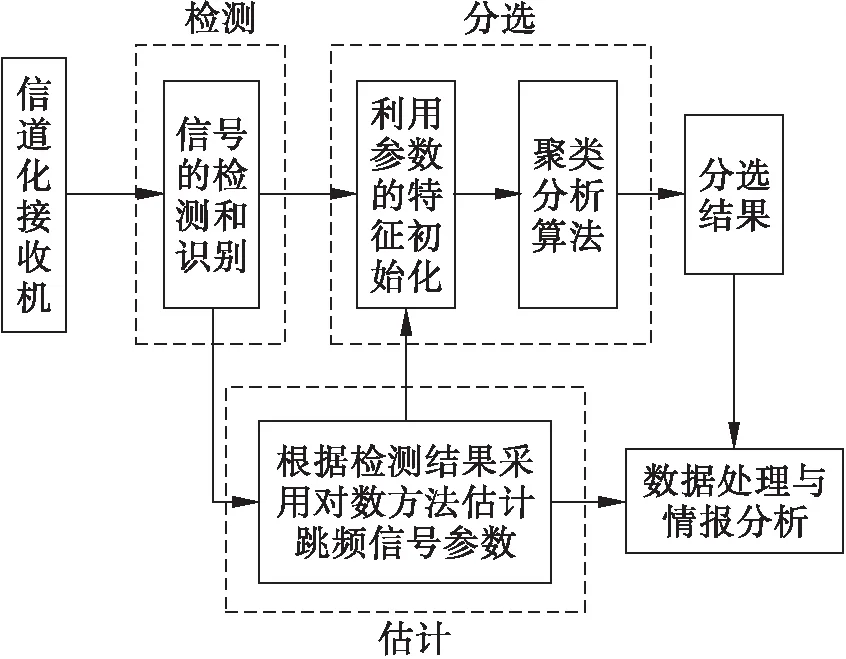
图1 跳频信号聚类分选方法的基体原理结构框图

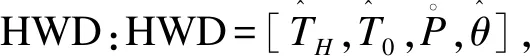
(1)

其中：xi为数据样本的特征矢量;N为待分类样本的个数，在本文中表示截获信号中所包含的跳数;每个样本矢量xi的维数为L=3。系统无论采用同步还是异步的方式进行跳频通信组网，每个跳频电台的HWD中的元素均存在较大差异，将式(1)输入到聚类算法中处理，可以将每个xi所代表的跳区分开，实现多个跳频信号的有效分选。

1.1 聚类分析算法

聚类分析是一种无监督的学习过程，利用样本自身的特征属性来识别数据集合内部的自然分组，将待分类的数据样本划分到不同类内，使得每个类的数据相似性最大。

聚类分析的过程由数据特征提取、相似度计算和聚类分组3部分组成。其中，数据特征提取是指选择最能代表数据样本特征的参数作为聚类算法的输入，本文中采用的数据特征为式(1)中的HWD；相似度计算是指利用度量函数来计算不同数据样本之间的相似性，为聚类分组提供依据；根据相似度计算结果，聚类分组采用一定的聚类准则将样本划分到不同类内。由以上的聚类过程可以看出，数据的相似性度量函数和聚类准则函数是算法的两个关键函数。

1.1.1 数据的相似性度量

不同样本之间的相似程度是对数据进行聚类分组的基础，最常用的相似性度量为距离测度，其值为任意两个样本的特征矢量xi和xj之差，包括明氏(Minkowski)距离、欧式(Euclidean)距离、绝对值距离和马氏(Mahalanobis)距离等。

Minkowski距离的定义为

(2)

Mahalanobis距离的定义为

d(xi,xj)=[(xi-xj)TΣ-1(xi-xj)]1/2,(i,j=1,…,N)

(3)

其中：Σ为特征矢量的协方差矩阵

(4)

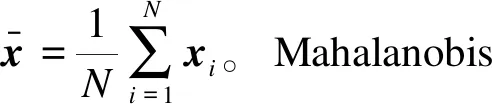
1.1.2 聚类准则函数

聚类准则函数又被称为代价函数，用于指导聚类的迭代过程，并判断当前的聚类结果是否满足分选的要求，以此决定是否结束迭代。准则函数的选择直接决定了聚类结果的质量，采用合适的准则函数可以得到更优的聚类效果，目前常用的准则函数为误差平方和(Sum of Squared Error, SSE)函数。假设待分数据{xi|i=1,…,N}被划分到K个类内ωk={xi,i=1,…,nk}，则SSE函数的定义如式(5)所示

(5)

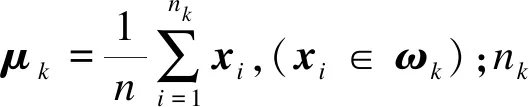
(6)

1.2 基于KHM的跳频信号分选方法

目前已经出现了多种聚类算法，主要包括：层次算法、划分算法、基于密度的算法以及基于模型的算法等[13-14]。其中，划分算法的基本思想是通过最优化代价函数将N个样本划分到k个类内，在聚类过程中能够动态调整聚类中心和类内样本，具有较好的聚类效果。K-Means算法为典型的划分算法，具有理论聚类效果好、执行效率高的优点，已经被广泛应用于各种与数据分类相关的领域，并且也是目前跳频信号聚类分选中采用最多的聚类算法。但是K-Means算法对中心点的初始值敏感，且容易收敛到局部最优值，在跳频参数估计误差较大的情况下，采用K-Means及其改进算法得到的分选结果不理想。在K-Means算法的基础上，文献[15]提出了一种KHM(K-Harmonic Means)聚类算法，采用调和平均数(Harmonic Aveage,HA)取代样本点到中心点之间的距离来构造目标函数JW，降低了聚类结果对聚类中心初始值的敏感度，提高了算法的聚类性能。

(7)

其中：K为聚类个数；N为样本个数；μk为第k类的中心点；xi∈RL则表示第i个样本的特征矢量，由L个特征参数估计值组成。

新的代价函数对聚类中心初始值鲁棒，与K-Means算法相比，KHM聚类算法可以得到更高的正确分选概率。为进一步改善算法，可采用直方图统计方法初始化聚类中心并预估计聚类个数。基于直方图统计KHM算法详细步骤如下：

步骤(1) 聚类初始化

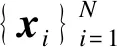
步骤(2)更新聚类中心

(8)

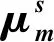
(9)

为避免式(8)出现分母为零的情况，在di,m=0时为di,m赋予极小值ε=10-6。

步骤(3) 终止迭代和聚类分组

将前后两次迭代得到的类中心进行比较，当最大值的均方误差满足一定精度时，停止迭代并对所有样本点进行聚类分组

(10)

其中：ki表示xi所属的类标识。否则，令s=s+1，返回步骤(2)继续执行。

2 改进的KHM聚类算法

2.1 基于有效性指标的聚类数估计值优化

直方图滤波处理的过程为：首先，计算滤波峰值门限η和邻域半径eps；然后，将峰值小于门限η的类舍弃，将峰值间距小于eps的类合并，以大的峰值作为合并后类的初始中心点。其中，门限η和邻域半径eps计算公式分别如式(11)所示

(11)

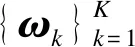
定义1：平均类内距。第k个聚类的第i个样本的类内距为xi到ωk内其他样本的平均距离，即

(12)

定义2：最小类间距。第k个聚类的第i个样本的最小类间距为xi到其他类样本平均距离的最小值，即

(13)

定义3：Sil-CVI。Sil-CVI定义为最小类间距和类内距的差值与两者之间最大值的比值，即

(14)

根据以上定义，平均类内距dI(xi,ωk)越小，表示类内样本的相似性越好；最小类间距dB-min(xi,ωk)越大，则表示不同类之间的分离程度越好；两者之间的差值dB-min(xi,ωk)-dI(xi,ωk)对类内样本的相似度和不同类间样本的分离度进行线性平衡，该值越大表示聚类效果越好。为避免有效性指标受量纲的影响，采用了dI(xi,ωk)和dB-min(xi,ωk)的最大值归一化，使Sil-CVI的取值在[-1,1]内。由此，最优的聚类数可以通过式(15)得到。

(15)

2.2 算法描述

本文给出一种改进的KHM聚类算法，其详细步骤如表1所示。为便于描述，将该聚类算法称为Sil-KHM算法，对应的跳频分选方法称为Sil-KHM方法。

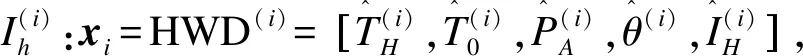
表1 Sil-KHM聚类算法的步骤

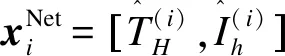
图2 基于分级策略和Sil-HKM算法的跳频信号分选方法流程

3 仿真实验

通过设置两组实验对基于Sil-KHM的跳频分选方法进行仿真，并将该方法与现有的K-Means方法和KHM方法相对比。实验1为基于TH和IH的混合跳频信号的跳频网络分选，实验2为基于T0、θ和PA的网内电台分选，实验参数见表2所示。每组实验的仿真次数NR=100，采用平均正确分选概率来衡量分选的性能。

(16)

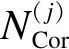
表2 跳频信号网络和电台分选实验的仿真参数

3.1 算法描述

本文采用跳周期和跳频方式二维参数进行跳频网络分选，在一定程度上可以提高分选性能。考虑到循环谱检测在跳频识别方面的良好性能(信噪比大于-10 dB时，跳频识别的正确概率可以达到100%，可假设IH的方差为一个极小值)，直接采用直方图统计值来初始化聚类中心和确定聚类数。图3给出了跳周期估计误差为1的情况下，跳频网络分选中的特征参数的直方图统计结果。由图3可以看出，仅采用直方图统计结果无法有效地确定真实的聚类个数。在引入跳频方式的信息以后，跳频网络的统计直方图非常清晰，很容易就能确定正确的聚类个数。

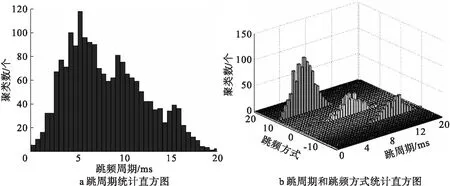
图3 跳频网络分选的特征参数的直方图统计结果

表3给出不同的跳周期估计误差条件下，分别采用K-Means方法、KHM方法和Sil-KHM方法得到的网络个数和平均正确分选概率。在跳周期的估计误差大于0.1 ms时，K-Means方法和KHM方法得到错误的聚类数所对应的平均正确分选概率远低于Sil-KHM方法，这是因为前两种方法利用图3a的统计结果来估计聚类数和初始化聚类中心，而后者采用的是图3b中的统计结果。在估计误差小于0.01 ms的条件下，3种方法均能得到正确的聚类数。由于KHM方法对聚类中心初始值的敏感度较低，因此可以获得比K-Means方法更高的正确分选概率。而由于Sil-KHM方法采用了识别精度高的IH作为特征矢量，可以获得100%的正确分选概率。

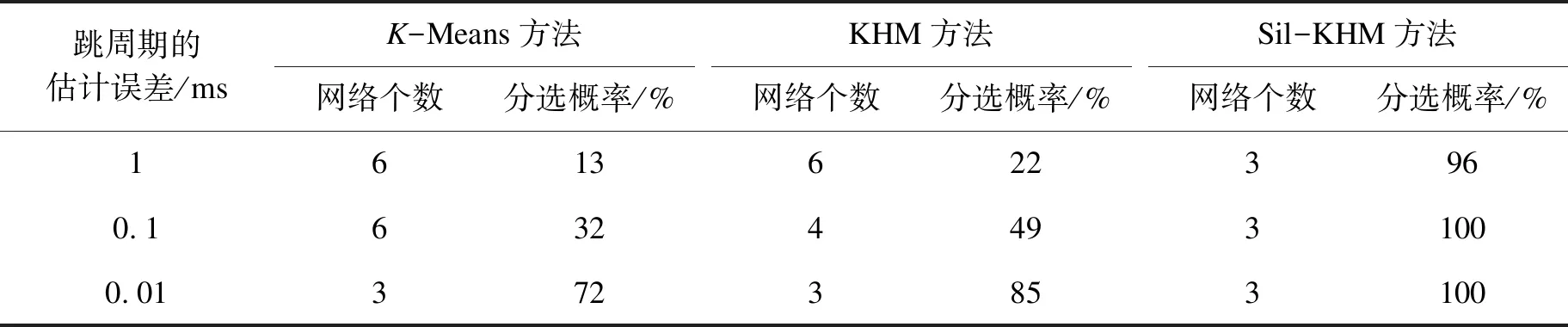
表3 跳频网络分选的结果

3.2 基于跳时、到达角和功率的网内电台分选

在对网络内的跳频电台进行聚类分选时，跳频方式不再作为特征矢量的参数，为提高聚类的质量，本文的方法需要采用有效指标来确定最优的聚类个数。表4给出了3种分选方法在不同估计方差下的聚类数估计结果，图4则给出了正确分选概率随参数估计方差变化的曲线。

由表4可以看出，由于Sil-KHM方法在初始化聚类中心的同时能够利用有效性指标对聚类个数进行优化，其得到的正确聚类的统计值大于其他两种方法。从图4中可以看出，由于Sil-KHM方法能够获得更为精确的聚类个数估计结果，因此其正确分选概率也优于其他两种跳频分选方法，分选概率均高于K-Means分选方法和KHM分选方法。

表4 3种分选方法聚类数估计结果

4 结论

本文将直方图统计方法与聚类有效性指标相结合，改进传统的KHM聚类算法，提出了一种新的Sil-KHM聚类算法。该算法利用聚类有效性指标对聚类个数进行优化，并且能够在分选的过程中确定最优的聚类个数，以增加较小的计算量为代价，有效提高了聚类分选的正确概率。仿真实验表明，在参数估计误差较大的条件下，与现有的跳频信号分选方法相比，基于Sil-KHM的跳频信号分选方法可以获得更高的正确分选概率，有效改善了跳频信号分选的性能。

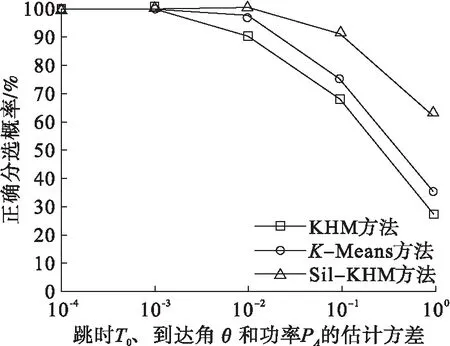
图4 正确分选概率随参数估计方差变化曲线