高动态下的星体目标质心提取方法*

潘 迪，温兆伦，任平川，陆 建，韩圣升

(1.上海航天控制技术研究所·上海·201109；2.上海市空间智能控制技术重点实验室·上海·201109)

0 引 言

星敏感器是以恒星为参考、以天空为工作对象的高精度空间姿态测量装置，具有重要的应用价值[1]。为了从星图中获得更高的星点定位精度，星敏感器的光学系统常常采用离焦的方式，使得静态条件下星点在探测器成像面上的像斑扩散为3×3至5×5的弥散圆，接着再利用细分定位算法提取星点质心，精度可达到亚像元级[2]。在星敏感器中,星点质心的定位尤为重要,其精度决定了星敏感器姿态测量的精度[3-4]。

星斑可以看作无穷远处的点光源在光学系统焦平面上所成的图像。当载体相对天球快速转动时，星点成像会出现拖尾现象[5]，即在单位曝光时间内，星点成像轨迹不可忽略时，星光所激发光电子以一定规律沿着轨迹分布的现象。在这种条件下,星点生成的星斑被称为动态星斑；与之相对的，在单位曝光时间内星点成像轨迹可以忽略时，星点的成像被称为静态星斑。载体的角速度越大，星斑拖尾长度越长，动态像斑的平均灰度值越低。如果以静态星斑的标准对动态星斑进行滤波，动态星斑很容易被当作背景杂散光被过滤掉，从而破坏质心提取的可靠性，这会对航天器的定姿产生重大影响。

高动态下的星点质心定位技术是近年来研究的热点。文献[5]建立了动态条件下的恒星成像模型,并利用模板补偿星斑缺失部分，有效提高了星点质心定位精度。但动态模板生成及星斑补偿算法过于简单，对于定位精度的提升效果有限。文献[6]则针对星点拖尾现象,提出了一种基于自适应窗口选择的星体目标提取方法，并基于数学形态学使断裂星体进行主动生长，完成了对于星斑的修补。但修补方法比较简单，容易造成像斑失真。针对高动态条件下的星点拖尾问题，本文提出了一种基于差异哈希的高动态条件下星点质心提取方法。首先,对星点动态像斑进行建模。其次，基于差异哈希算法与上述模型对星跟踪模式下窗口内的星体目标进行粗定位，并对粗定位区域采用阈值分割与连通域法[2](下述“传统法”)提取星点质心。通过这样由粗到细的星点质心提取方法，以克服传统方法在高动态情况下星点提取率低、质心提取精度不高的问题。最后，使用外场观星实验的数据完成算法的仿真，验证了算法的有效性。

1 基于差异哈希算法的星点质心提取方法

针对传统法在高动态下无法准确提取星点质心的问题，本文提出了一种星跟踪模式下波门内星点质心提取方法。首先对动态星斑进行数据建模，接着采用差异哈希算法将星斑模板及波门子图映射为固定长度的哈希值，随后利用汉明距离对模板哈希值及波门子图哈希值进行相似性检测，找出波门图中与模板最相似的子图，实现在星跟踪波门内的星体粗定位，最后在星点粗定位区域使用传统法提取质心。算法的整体流程图如图1所示。

图1 算法流程图Fig.1 The flowchart of the algorithm

1.1 动态星斑建模

星敏感器所探测的目标是无穷远处的恒星。理想情况下，静态星斑的能量分布符合二维高斯分布[7-8]

(1)

式中，I(x,y)为探测器成像平面坐标为(x,y)像元所接收的光电子数；(x0,y0)为星点像斑的质心；σ为高斯半径；A为一正比于总光强的比例系数。在光学设计中常使用均方根(Root Mean Square，RMS)半径rrms来表示弥散斑的半径，显然σ与rrms两者在数学上满足

(2)

所以，静态条件下，星敏感器探测器像面波门内的光电子分布为

(3)

其中，Ne为激发光电子数，正比于波门内的总灰度值。

以某型星敏感器为例，其探测器像元尺寸为18μm，光学系统保证的弥散斑半径为25μm，则恒星在该探测器上成像的弥散光斑有80%以上的能量集中于3×3的像元内。坐标(m,n)的像元内激发电子数满足关系

xp0)]}{erf[k(n-yp0)]-erf[k(n+

1-yp0)]}

(4)

(5)

其中，erf(x)函数值可以通过查表得到。

高动态条件下，因为曝光时间很短，所以可以认为星点质心在探测器成像面上的运动为匀速运动。则动态情况下，坐标(m,n)的像元内激发电子数变成

erf[k(m+1-xp0-vxpt)]}·

{erf[k(m-xp0-vxpt)]-

erf[k(m+1-xp0-vxpt)]}dt

(6)

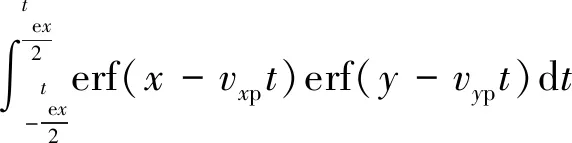
(7)

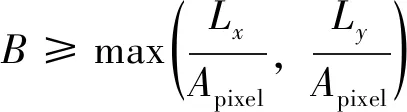
(8)

所以，可以将式(7)改写为级数形式

(9)

这样就得到了已知速度、曝光时间、像元尺寸和镜头rrms，求取星斑在波门任一像元内的受激发光电子数的方法。该数值正比于像元的灰度值，在只关注像元间灰度的相对关系时，可以不用计算精确的Ne值，将其设置为常数。图2即为使用式(9)生成尺寸为8×9的星斑模板。

1.2 基于差异哈希算法的星体目标粗定位

哈希算法又称为散列技术，它将任意长度的二进制值映射为较短的固定长度的二进制值，即为哈希值。哈希值是一段数据唯一且极其紧凑的数值表示形式。哈希算法主要用于验证原始数据是否被篡改。而在图像相似性检测上，通常使用感知哈希算法，它的作用是对每张图片生成一个指纹字符串，然后比较不同图片的指纹，结果越接近，就说明图片越相似[9]。感知哈希算法是一类算法的总称，包括平均值哈希(Average Hash, AHash)、感知哈希(Perceptual Hash，PHash)和差异哈希(Difference Hash，DHash)。感知哈希不是以严格的方式计算哈希值，而是以更加相对的方式计算哈希值，因为相似与否就是一种相对的判定。

(a) 星斑模板图像

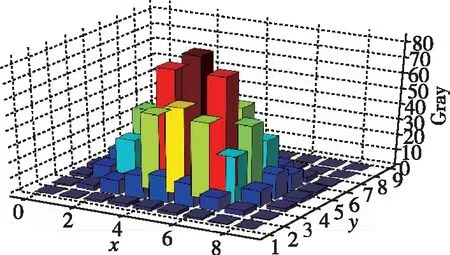
(b) 星斑模板3维图像图2 星斑模板图像Fig.2 Dynamic star spot template

由1.1节可知，动态星点像斑在相邻像元间的相对灰度分布有明显的规律性，且在光学系统确定的条件下，这种规律性只与星敏感器的转动速度有关，与恒星本身的能量无关。差异哈希算法中的差异值是通过对比每行相邻像素的灰度得出的，这标识了灰度的渐变方向。所以对于每一帧的星跟踪波门，可以通过计算模板和窗口子图的差异哈希值进行图片相似性检测，与模板最相似的子图即为星体目标粗定位区域。算法流程如下：

1)计算模板的差异哈希值DHashtem。按式(9)生成8×9的动态星斑模板矩阵，模板星点质心取在矩阵中心。比较每一行左边像素与右边像素的灰度值，若左边像素的灰度值大于右边，则差异哈希值设置为1，否则设置为0。这样就得到了8个差异哈希值数组，每个数组中含有8个差异哈希值。将每个差异值看作1bit，每8个bit组成一个16进制值，将8个16进制值转化为字符串并连接起来，就得到了模板的差异哈希值DHashtem。以图3为例，该模板的差异哈希值为“0f0f0f0f0f0f0f0f”。

(a) 星斑模板矩阵

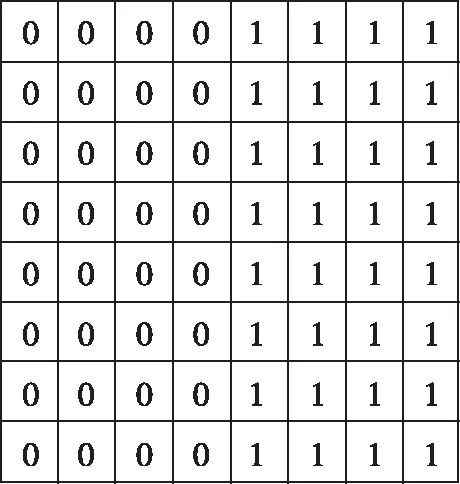
(b) 星斑模板差异哈希数组图3 星斑模板差异哈希值生成过程Fig.3 The generation process of DHash value of the template

2)计算波门的差异哈希值DHashi,j。假设跟踪窗口图像的大小为N×M，在窗口内以n×m的小窗口作滑动窗口，截取窗口子图，则会得到(N-n+1)×(M-m+1)个与模板尺寸相同的窗口子图。按上述方法计算每一个窗口子图的差异哈希值，记为DHashi,j，其中i，j为子图左上角在原窗口内的坐标。

3) 使用汉明距离比较模板的差异哈希值与所有模板子图的差异哈希值，取最小值为最佳匹配区域。在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。因为前文已经将模板与子图都转换成了差异哈希字符串，所以可以使用汉明距离来度量两幅图片的相似性。与DHashtem汉明距离最小的DHashi,j表征了窗口中与模板最相似的子图，该子图就是星体粗匹配区域det。

1.3 使用传统法提取星点质心

连通域与阈值分割法是最传统的基于灰度的质心提取方法，也是目前运用最广泛的方法[2]。首先对星点粗匹配区域进行滤波，其次提取滤波后窗口内的四连通域，最后采用质心法在四连通域内计算星点质心。这样由粗到细的质心提取方法，能够克服传统法在高动态、大波门情况下星点提取率低、质心提取精度不高的问题。

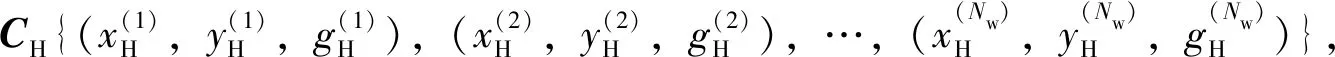
(10)

2 实验结果与分析

2.1 实验条件

实验采用的数据为某型号星敏感器2021年7月31日的外场地面观星LVDS下传的波门数据，某型号星敏感器的光学系统参数如表1所示。

表1 某型号星敏感器光学系统参数

实验分为两组，每一组皆分别使用差异哈希值法与传统法提取窗口内的星点质心。在处理每一帧窗口数据时，模板由处理器直接计算。两组实验中的每一次测试，皆选取星跟踪模式下的100帧波门图像作为实验数据。第一组实验，曝光时间设定为恒定值86ms，设定转台转动速度，使星敏感器的合成角速度分别大约为1(°)/s、2(°)/s和3(°)/s，测试3种星点提取方法在不同角速度下对星敏感器定姿精度的影响。第二组实验，转台转速设定为恒定值3.1(°)/s，设定3组不同的曝光时间86.5ms、62.5ms和50ms，测试3种星点提取方法在不同曝光时间下对星敏感器定姿精度的影响。

2.2 评价指标

本文采用星对角距误差和单帧提取率作为算法的评价指标。

(1)星对角距误差

在高动态情况下，传统的基于滑动窗口的误差计算方法不再适用[10]。本文鉴于星对角距的不变性，采用视场内星对角距统计偏差评估星敏感器的姿态测量精度[11]

(11)

其中，Nstar为当前帧视场中的定姿星数；b和v分别为标准星矢量和测量星矢量；l代表帧号。

(2)数据有效率

数据有效率是有效帧数与总帧数的比值。如果当前帧识别匹配成功的定姿星在3颗以上，则判定其为有效帧。

(3)单帧提取率

单帧提取率为一帧中成功提取的探测星数与视场中所有导航星数的比值。若算法能够成功输出星点质心，则判定星点提取成功。

2.3 实验结果

实验一，分别用传统法和相关模板匹配法提取星点质心，采用上述3种评价指标对2种算法进行评价，评价结果如表2所示，星对角距误差曲线如图4所示。其中星对角距误差统计了100帧误差的均值和三倍标准差(3σ)，提取率统计了100帧提取率的均值(Mean)、最大值(Max)和最小值(Min)。

从图4和表2可以看出，相关匹配法的星对角距误差较为稳定，在角速度1(°)/s、2(°)/s和3(°)/s的高动态条件下，星对角距误差均值较传统法分别减小了47.4%、42.7%、34.7%。从提取率上来评价，差异哈希法能够稳定提取星点，100帧的平均提取率达到100%；而传统法提取率较低且不稳定。从数据有效率上看，相关匹配法在3种角速度下，100帧数据全部有效，能够稳定输出姿态信息；而传统法随着角速度的增大，数据有效率逐渐降低，出现了跟踪失败的情况。以上实验结果表明，差异哈希法在高动态情况下能够实现恒星的稳定跟踪，且误差稳定，精度符合星敏感器的指标要求。

实验二评价结果如表3所示，星对角距误差曲线如图5所示。

表2 实验一评价结果

(a) 1(°)/s

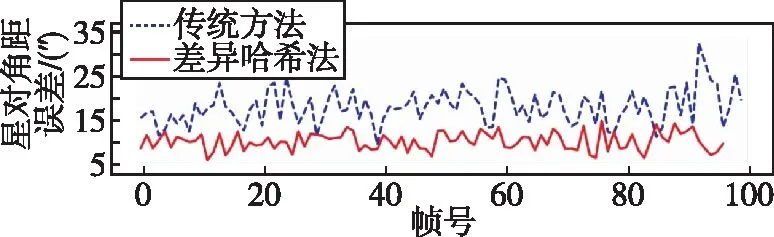
(b) 2(°)/s

(c) 3(°)/s

表3 实验二评价结果

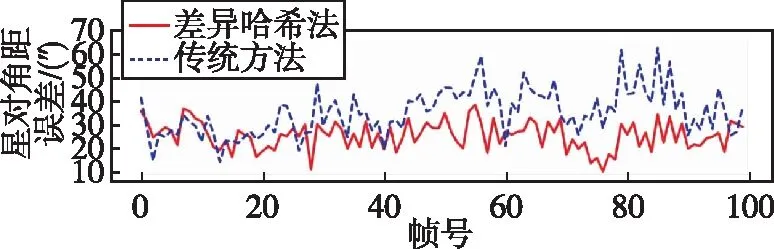
(a) 86ms

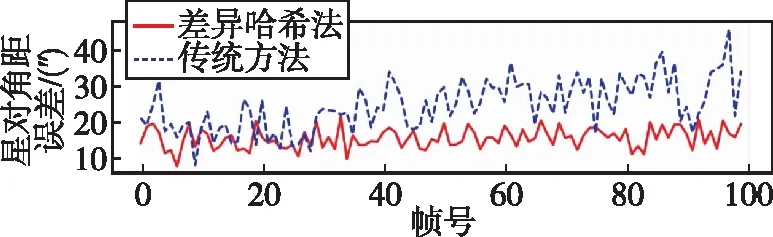
(b) 62.5ms

(c) 50ms图5 3种曝光时间下的星对角距误差曲线Fig.5 Angle distance error curves of two star point extraction methods under three exposure times

从图5和表3可以看出，随着曝光时间的缩短，2种方法的星对角距误差都有了大幅度的降低。相比较而言，差异哈希法的星对角距误差更为稳定，在曝光时间为86ms、62.5ms和50ms的条件下，误差均值较传统方法分别减小了34.7%、29.1%、29.6%。从提取率上来评价，对于3种曝光时间，相关匹配法能保证提取率在90%以上；而传统法的提取率均值达不到90%。从数据有效率上看，随着曝光时间的降低，传统法的数据有效率逐渐降低，出现了跟踪失败的情况；而相关匹配法在3种曝光时间下，数据有效率100%，能够稳定输出姿态信息。以上实验结果表明，差异哈希法在高动态下能够适应多种曝光时间，在实现稳定跟踪的同时提高定姿精度。在角速度3(°)/s 及曝光时间50ms的条件下，差异哈希法的星对角距误差均值达到13″。

3 结 论

本文针对高动态情况下星点目标提取困难的问题，提出了一种基于差异哈希的高动态条件下星点质心提取方法。此方法首先建立动态星点像斑的数学模型，其次利用差异哈希算法与汉明距离对模板图像与窗口子图进行相似度度量，实现对星跟踪模式下窗口内的星体目标粗定位，接着在粗定位区域采用传统法提取星点质心，这样由粗到细的星点质心提取方法能够克服直接在波门内使用传统法在高动态情况下星点提取率低、质心提取精度不高的问题。基于外场观星数据的仿真实验表明，本文提出的星点提取方法能够实现星敏感器在角速度3(°)/s条件下的稳定跟踪，并且能够适应各种长度的曝光时间。在曝光时间50ms，角速度3(°)/s的条件下，星对角距误差为13″，平均提取率为96%，相较于传统方法，分别提高了29.6%和22.9%。