数控机床电气设备电源频率智能控制技术研究

王 丽

（广东省技师学院，广东 惠州 516100）

0 引言

零件加工是工业生产中的一个重要方面。早期零件加工主要是由人工完成，后来逐渐发展成半自动化方式，但是仍无法满足小批量零件的要求。面对这种情况，数控机床被发明出来并广泛应用于小批量零件的加工中。在数控机床中设定好程序就可以控制前端加工工具完成零件加工。虽然数控机床很大程度上弥补了小零件加工的缺陷，但是随着零件复杂程度、精密程度要求的提高，提高数控机床的控制质量势在必行，其中控制数控机床电气设备电源频率就是一个重要方面。关于电源频率控制的问题，刘宁庄、张远宝和许龙等人利用FFT 采集相位差信号和输出功率信号，然后以此为输入，利用模糊PID 得出控制信号，控制电源频率[1]。丁艳华、郑宏和肖凤等人以采集到的相位误差信号为基础，利用PSO-PID 计算得出驱动信号，实现电源频率控制[2]。结合前人研究经验，该文提出了一种数控机床电气设备电源频率智能控制技术。

1 电源频率智能控制模型构建

电源频率智能控制是保证电气设备稳定运行的前提，电源频率控制质量越高，电气设备运行就越稳定，零件加工精度就越高。基于此，该文为研究了一种数控机床电气设备电源频率智能控制技术。该技术主要分为3 个部分，即电源频率信号采集与预处理、理想电源频率求取以及电源频率智能控制实现。下面针对这3 个步骤进行分析。

1.1 电源频率信号采集与预处理

电源频率的控制的目的是让其不断无限接近理想电源频率，使二者之间的差值一直在可控的范围内。基于此，实时监测电源频率信号是控制实现的第一步。在这里需要利用的采集设备为电源频率信号测量输出检试仪。它将感知到的电源频率转换成电信号，再经过放大调制，输出电源频率信号[3]。

采集到的电源信号通过无线通信设备发送给上位机后需要进行预处理，以提高信号质量。预处理工作的任务是去除信号中的噪声，实现信号滤波，具体过程如下。

步骤1：输入采集到的电源频率信号，记为a（t）。

步骤2：在电源频率信号a（t）中加入高斯白噪声bi（t），得到混合信号ci（t）。其中i代表高斯白噪声的加入次数。

步骤3：利用模态分解方法对ci（t）进行分解，将其分为若干个IMF 分量和一个残差分量。分解结果如公式（1）所示。

式中：di（t）为第i个IMF 分量；r（t）为残差分量。

步骤4：对公式（1）中若干个di（t）分量求取平均值，得到一个从高频到低频依次排列的IMF 分量。

在以往的处理中，往往不需要上述信号分解的步骤，而是通过小波阈值方法去除其中噪声的干扰。然而小波阈值是集中去噪的，有时造成的隐藏性较大，去除效果并不理想。基于此，该文先通过分解再去除，不仅能够提高去噪效果，还大大减少了去噪工作量。小波阈值去噪流程如下：先选定小波阈值去噪的基础函数，即小波基函数。小波基函数的类型有很多，在这里选择其中地Biorthogonal。接下来确定分解层数和分解尺度。由于上述已经利用集合经验模态分解方法分解了电源频率信号，在这里就不需要分解了，上述IMF 分量的数量就是Biorthogonal 小波基函数对电源频率信号的分解层数，将分解尺度设置为L。利用Biorthogonal 小波基函数对每层电源频率信号进行处理，得到尺度为j的第k层处理结果Djk。然后确定阈值，构建阈值函数，该函数如公式（2）所示。

式中：Djk为阈值函数；V为阈值；Djk为尺度为j的第k层小波系数。

通过Djk得到小波系数，进而重构小波系数，就可得到去噪后的电源频率信号。对电源频率信号进行去噪处理，其中的噪声被有效剔除干净，这样信号数值会更准确，非常有利于最后的控制，可提高控制质量。

1.2 理想电源频率求取

在控制研究中，只获取实际数控机床电气设备电源频率还不够，还需要知道理想电源频率，即希望达到的电源频率值。当控制某一参数让实际电源频率接近或等于理想电源频率值时，就实现了数控机床电气设备电源频率的控制。而某一参数的控制也被称为控制量的求取过程，也即控制方案的设计过程[4]。而控制量的求取是由实际电源频率与理想电源频率的差值通过运算得到的。基于此，就需要求取理想电源频率。此处需要利用多元回归模型。电源频率的变化受很多因素的影响，每个因素的变化都会带来电源频率的改变，由此可以看出影响因素与电源频率之间存在线性关系，二者之间的关系如公式（3）所示。

式中：Z为因变量（电源频率）；R1，R2，...，Rn为自变量（影响因素）；w0，w1，w2，...，wn为回归系数。

公式（3）是一个预测方程。在此方程中，自变量和因变量都可以通过历史数据获得，是已知的，但是回归系数w0，w1，w2，...，wn则是未知的。但要想预测未来理想电源频率，回归系数必须明确。针对这一点，可以利用已知的历史电源频率和对应的历史影响因素建立方程组，然后利用最小二乘估计方法求解，就可以得到回归系数w0，w1，w2，...，wn。得到回归系数w0，w1，w2，...，wn之后，代回到公式（3）中，得到完整的电源频率预测模型。为保证该模型的有效性，还需要对模型进行检验。检验有3 种，具体见表1。

表1 多元回归模型检验

当上述3 种检验都通过后，就正式完成了预测模型的构建。这时只要输入当下时刻的影响因素，就能够预测出理想电源频率。

1.3 电源频率智能控制实现

基于上述研究成果，该文构建了一种控制模型。该模型是以PID 控制器为核心建立起来的，如图1 所示。

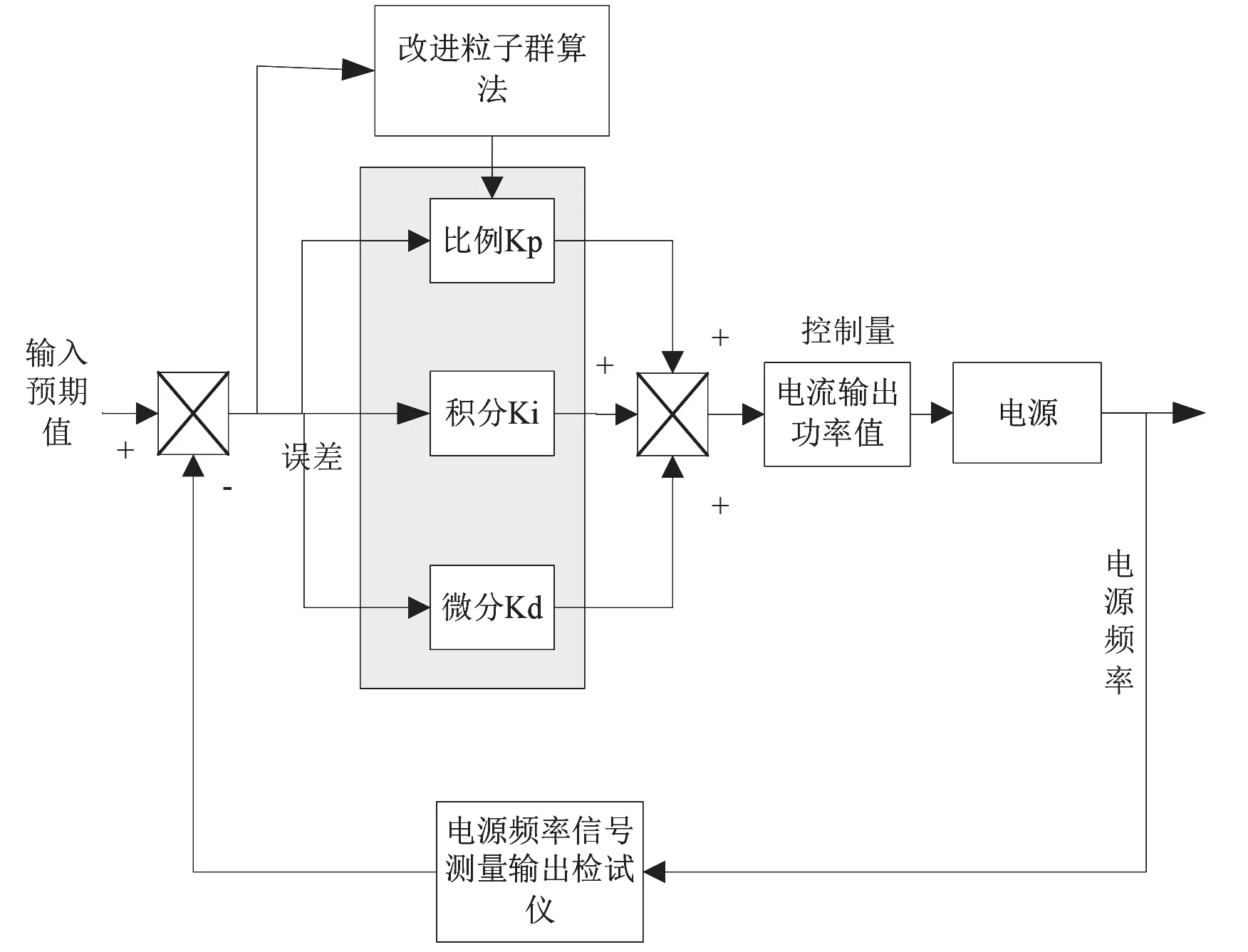
图1 电源频率智能控制模型

从上述模型可以看出，以理想电源频率和实际电源频率之间差值为输入，然后经过比例、积分和微分三种运算得到控制量。控制模型基本表达式如公式（4）、公式（5）所示。

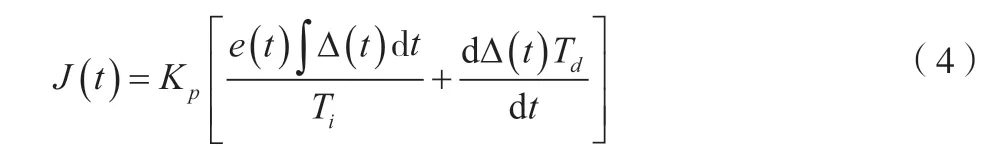
式中：J（t）为数控机床电气设备电源频率的控制量，这里指的是电流输出功率，功率值越大，电源的运行频率越高。因此通过控制电流输出功率，就可实现电源频率的控制；∆（t）为理想电源频率和实际电源频率之间差值；Kp为比例系数；Ti为积分时间常数；Td为微分时间常数；b（t）为理想电源频率；q（t）为实际电源频率。

在上述模型中，3 种运算负责不同的工作，其中比例运算负责感应误差的存在，对误差进行处理[5]，可以调整误差的大小；积分运算负责消除静差，提高控制模型的稳定性；微分运算组负责数据预测。这3 个运算是整个控制模型的关键。虽然利用这3 个基础运算也能得到控制量数值，但是很容易产生“快速性”和“超调”之间的矛盾，影响控制模型的可靠性[6]。面对这种情况，一般在构建完上述基础PID 控制模型后，还需要对比例、积分和微分进行整定。在这里采用的整定方法为改进粒子群算法，具体过程如下。

步骤1：设置粒子群算法参数。

步骤2：初始化粒子群，建立粒子群空间。3 个参数整定就是在3 个参数的空间中寻找最优值。空间中每个粒子都是参数在三维空间中以实数编码。

步骤3：利用公式（6）所示的适应度函数计算每个粒子的适应度。

式中：N为时间绝对偏差积分。

步骤4：将计算出来的每个粒子的R与局部最优值和全局最优值进行比较。如何前者大于后两者，则让R替代后两者，否则保持不变。

步骤5：更新粒子速度和位置。

步骤6：检测粒子聚合度。

步骤7：对粒子执行遗传操作。

步骤8：回到步骤3，重新计算粒子适应度，再次更新粒子速度和位置。

步骤9：判断是否达到结束条件。如果是，输出最优结果，得到最优PID 参数；否则重新计算粒子适应度值，重复上述过程。

经过粒子群算法的整定后，将3 个参数代入公式（4）中，以实现数控机床电气设备电源频率智能控制模型的优化。

2 试验测试与分析

为测定所研究的控制方法在数控机床电气设备电源频率智能控制中的应用性能，以3 种数控机床电气设备为例，与基于模糊PID 的控制方法、基于PSO-PID 的控制方法一起在MATLAB 上进行测试。

2.1 电源频率数据

基于1.1 节的研究，利用电源频率信号测量输出检试仪采集3 种数控机床电气设备电源频率数据，采集时间设置为20s。采集结果见表2。

表2 电源频率历史数据（单位：Hz）

电压应力、电流应力、负荷功率、PWM 的死区时间、开关损耗是影响电源频率的主要因素，因此将这5 个因素作为自变量，获取20s 内这5 个因素相应的数值，结合表2 建立方程组，然后利用最小二乘估计方法求解，就可以得到回归系数，分别为1.2551、0.87465、-2.8645、3.8741、1.8452。通过检验后，建立理想电源频率预测模型，得到理想电源频率。

2.2 电源频率控制方案

基于1.3 节的研究，利用控制模型计算控制量[7]，即电流输出功率。相同条件下，利用基于模糊PID 的控制方法、基于PSO-PID 的控制方法进行控制，得出控制方案。结果如图2 所示。

2.3 控制效果分析

利用图2 得到3 种控制方案实时控制电源频率，让其实际电源频率波动无限接近理想情况。根据控制结果，计算与理想结果之间的电源频率波动指数。如公式（7）所示。

图2 电源频率控制方案

式中：g为电源频率波动指数，该指标越小代表方法控制效果越好；Ht为应用控制方法时t时刻的电源频率；ht为t时刻的理想电源频率；Pt、Qt为应用其余两种控制方法时的t时刻的电源频率。

求取3种方法控制下的3个电气设备电源频率波动指数的平均值，控制效果见表3。

表3 电源频率波动指数平均值

从表3 可以看出，在所研究方法的控制下，实际控制结果与理想之间的波动指数要小于其余两种方法。由此可知在所研究方法的控制下，数控机床电气设备电源频率更接近理想情况，控制质量更高。

3 结语

随着零件加工质量要求的不断提高，数控机床电气设备电源频率的控制问题越来越受到重视，其频率大小直接关系到数控机床的运行稳定性。为此，该文研究了一种基于数控机床电气设备电源频率智能控制技术。该技术通过计算电源频率的误差，利用改进PID 得出控制量，实现了电源频率的有效控制。最后通过试验测试，证明了所研究的控制方法控制效果要好于前人研究的两种方法。