广义回归神经网络高程插值方法研究

王吉凯

（中国人民解放军61175 部队，江苏 南京 210000）

0 引言

数字高程模型是在二维空间上对三维地形表面的客观表达，它在二维平面上对研究区域进行网格划分，形成格网空间架构，以覆盖整个区域。地理学分析中的数字高程模型作为等高线地形图的替代产品，其是科学研究、经济建设和国防建设的基础数据和有力工具，也是地理学分析、生物学等区域性科学基本参数的提供者和科学研究成果的表现形式。同时，各种不同分辨率的数字高程模型是数字绘图和综合必需数据[1]。在数字高程模型建立过程中的重要内容是格网点的高程内插计算，内插计算是构建数字高程模型的核心内容，贯穿了数字高距离模型的生产、品质控制、精度评价以及分析应用的所有环节[2]。在DEM 数据内插研究过程中，研究人员不仅对各种传统方法在地形表面建模中的可行性、特点进行了充分而深入的研究，而且也引进相关学科的内插方法（例如克里金、有限元等内插技术），同时根据地形表面的特点发展地形数据的各种内插方法。

该文利用实际测量的GPS 数据，运用广义回归神经网络算法、反距离权法、普通克里格法以及多项式插值法对地形高程插值进行研究。

1 地表高程插值

1.1 基本概念

广义回归神经网络是基于径向基网络的一种演变算法。该算法基于非参数回归算法，使用样本集充当验证数据，运用Parzen 非参数估计，以最大概率原则输出广义回归神经网络的运算结果。非线性逼近能力十分优异，与径向基相比，训练更方便，广义回归神经网络非常适合解决曲线拟合的问题。

x、y为随机变量，其联合概率密度为f（x，y），假设x的观测值为x0，对y进行求导，那么y对x的回归E（y|x0）如公式（1）所示。

那么在输入为x0的情况下，y的输出预测即为y（x0）。执行Parzen 非参数估计，得到样本数据集{xi，yi}，根据公式（2）估计密度函数f（x0，y）。

式中：n为样本容量；p为随机变量x的维数；σ为光滑因子，也就是高斯函数的标准差。

密度函数f（x0，y）公式中导数d（x0，xi）和d（y，yi）分别为x数据集xi的均方根误差和y数据集yi的方差，如公式（3）所示。

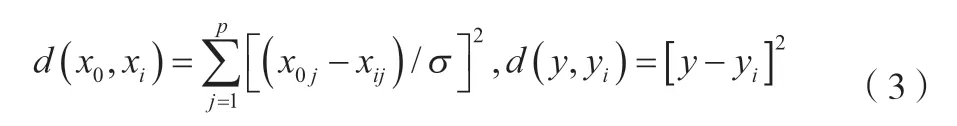
将公式（3）的d（x0，xi）代入密度函数，并交换求和与积分顺序，如公式（4）所示。

式中：分子为所有训练样本算得的yi值的加权和；e-d（x0，xi）为权值。

广义回归神经网络不需要训练，但是平滑因子的值对网络性能有很大的影响，并且需要优化值。如果光滑因子取值非常大，那么d（x0，xi）趋近于0，y（x0）近似于所有样本因变量的平均值。如果光滑因子趋近于0，那么y（x0）与训练样本的值非常接近，当需要预测的点在训练样本时，算得的预测值与样本中的期望输出非常接近，但是一旦给定新的输入，预测的结果就会急剧变差，使网络失去推广能力，这种现象就是过学习[3]。

广义回归神经网络由4 层构成，即输入层、模式层、求和层和输出层。设输入层为X=[x1，x2，...，xn]T，其输出层为Y=[y1，y2，...，yn]T。

1.1.1 输入层

输入层神经元的数量等于学习样本中输入向量的维数，每个神经元是简单的分布单位，并且将输入变量直接传递到模式层[4]。

1.1.2 模式层

模式层神经元的数目等于学习样本的数目n，每个神经元对应不同的样本，而模式层神经元传递函数如公式（6）所示。

式中：σ为样本标准差；X为网络输入变量；Xi为第i个神经元对应的学习样本[4]。

神经元i的输出为输入变量与其对应的样本X之间Eucd距离平方的指数平方Di2=（X-Xi）T（X-Xi）的指数形式。

1.1.3 求和层

在求和层中，使用2 种神经元进行求和。

第一种求和如公式（7）所示。

它对所有模式层神经元的输出进行算术求和，其模式层与各神经元的连接权值为1，传递函数如公式（8）所示[4]。

式中：SD为传递函数。

第二种求和如公式（9）所示。

它对所有模式层的神经元进行加权求和，模式层中第i个神经元与求和层中第j个分子求和神经元之间的连接权值为第i个输出样本Yi中的第j个元素，传递函数如公式（10）所示[4]。

式中：k为无限值（因为式中存在n，所以用k代指）。

1.1.4 输出层

输出层中的神经元数目等于学习样本中输出向量的维数k，各神经元与求和层的输出相除，神经元j的输出对应估计结果（X）的第j个元素，如公式（11）所示[4]。

1.2 数据处理

使用MATLAB 编程实现广义回归神经网络对高程进行预测的功能，输入归一化后的信号X、Y通过中间节点（隐层点）作用于输出节点，经过非线形变换产生输出信号Z，并反归一化X、Y值[5]。广义回归神经网络的所有训练样本为输入值X、输入值Y、期望值Z0以及输出值Z与期望值Z0的偏差。调节隐层与输入节点的连接强度、隐层与输出节点的连接强度以及阈值，使偏差沿梯度下降，通过不断训练学习，最终确定与最小误差相适应的权值和阈值。经过学习训练的神经网络算法可以自动对相似的样本信息进行计算，输出拟合程度最高的结果。

该程序设置学习率为0.01，训练精度要求为0.000 1，最大训练次数为10 000 次，网络输入向量的最大值和最小值为归一化后X、Y的最大值和最小值，设置每层神经元个数，共设3 层神经元，每层个数分别为15、40 和1。误差反向传播神经网络算法的隐含层的传递函数是“S”形函数，输出层是线性函数。前两层使用双正切“S”形函数传输函数，“S”形函数（Sigmoid function）是误差反向传播神经网络算法中常用的非线性作用函数，由于误差反向传播神经网络算法的传递函数必须可微，因此一般使用“S”形函数或者线性函数作为传递函数。第三层为线性传输函数。

选定Levenberg-Marquardt 训练函数，莱文拜格－马夸特方法（Levenberg–Marquardt algorithm）能计算数值非线性最小化的解。该方法可以通过在计算时修改参数来实现梯度下降法和高斯算法的优点，并优化这2 种方法的缺点。核心思想就是用雅可比矩阵代替H 矩阵的计算，从而提高优化效率。莱文拜格－马夸特方法的优点是可以优化调节，一旦下降过快，就可以改变参数，使用小的阻尼系数λ，使该算法与高斯法类似，一旦下降过慢，就可以改变参数，使用更大的λ，使算法与梯度下降法类似。

使用该神经网络输出预期值Z与实际值Z0进行比较，得出预测精度，并使用神经网络得出该地区所有高程值并可视化，得到的平面地形图和三维地形图如图1 和图2 所示。

图1 带点地形图

图2 三维地形图

2 预测精度评价

该文采用广义回归神经网络法、反距离权重法、克里格法以及多项式法的地表高程插值得到预测结果，并进行精度验证和评价分析，得出预测值与验证数据高程值对比，如图3 所示。

由图3 可知，数据点由低到高的离散程度逐渐变大，广义回归网络方法在整个高程范围内的数据点距拟合线平均距离最近，近似呈线性分布，拟合程度最高，其他方法随着高程的增加逐渐变高，数据点离散程度提高，拟合程度逐渐降低。综上所述，GRNN 方法拟合程度最高，其插值数据逐渐接近验证数据。

图3 离散回归点线图

该文用均方根误差（RMSE）、方差（SSE）以及确定系数（R2）来评价预测精度，见表1。

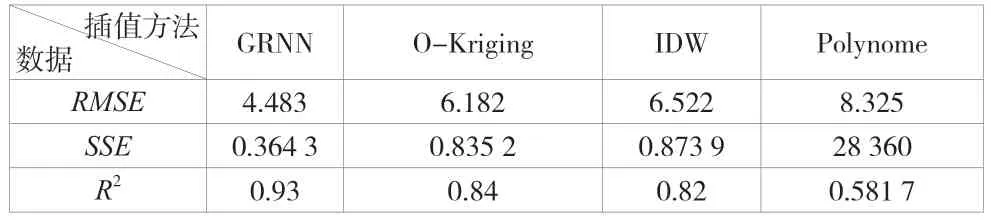
表1 精度指数

对比发现，在4 种方法中，广义回归神经网络算法的均方根误差、方差最小，确定系数最接近1。说明在样本数据的数目和分布状况均相同的条件下，广义回归神经网络算法的插值精度最高，且使用广义回归神经网络算法得到的均方根误差的值达到比较理想的值（5）附近。综上所述，广义回归神经网络算法是4 种方法中最适合该地区进行地形拟合的插值算法。

3 结语

该文以陕西省延安市安塞地区GNSS 实测高程数据为基础，分别采用GRNN、O-Kriging、IDW 以及Polynome 方法对样本点进行高程插值及精度验证。结果表明，在样本数据一定的情况下，GRNN 方法的插值精度明显高于其他方法，是最适合该地形区域的插值算法。试验证明该高程插值方法能够较准确地插值未测量地区的高程，但是不能满足对工程施工的精度要求，目前只能作为非精密测量区域的地形参考。且各种地表高程插值方法适用的地形特征不同，在实际使用过程中可能需要尝试多种方法，以比较预测精度。