采用复合模块化结构的海上风电送出直流变换器
2022-02-02刘其辉樊双婕洪诚程郭小江汤海雁申旭辉
刘其辉,樊双婕,洪诚程,郭小江,汤海雁,申旭辉
(1. 新能源电力系统国家重点实验室(华北电力大学),北京市 102206;2. 中国华能集团清洁能源技术研究院有限公司,北京市 102209)
0 引言
在“双碳”目标驱动下,海上风电发展迅速,截至2021 年9 月底,中国海上风电的累计装机容量达到13.19 GW[1],随着海上风电向深远海发展以及容量的不断增加[2],采用“直流汇集-直流传输”方式的全直流海上风电场避免了传统的“交流汇集-交流传输”方式下工频交流变压器体积大、传输距离受限等问题,受到了各国研究学者的热议。
目前,直流汇集方式下系统组网结构的确定及对关键设备的研制是全直流海上风电场的主要挑战。全直流海上风电场的组网结构可分为串联升压型[3-5]与并联辐射型[6],后者进一步分为集中升压、机端升压以及两级升压系统[6]。其中,两级升压的并联辐射型结构由于具有变换器设计与制造较容易、汇集损耗低、风机间耦合度低等优点,可将其作为全直流海上风电场的优选结构,而高压送出DC/DC 变换器作为关键设备,需要突破高电压、大功率直流电力变换难题,成为海上风电全直流组网的技术瓶颈和国内外业界研究的热点。
传统DC/DC 变换器能够承受的电压低、容量小,可将绝缘栅双极型晶体管(IGBT)器件串并联以适应全直流海上风电场的电能汇集需求,但器件间的均压、均流控制复杂。文献[7]通过将多个双有源桥(dual active bridge,DAB)DC/DC 变换器输入输出串并联,避免了开关器件的串联均压与并联均流的难题,但交流变压器数目增多,体积增大,且故障下变换器运行可靠性也会降低。文献[8]在DAB模块之间加入开关谐振支路,能够实现各模块输入电压的自动均压,但随着容量与电压水平的提高,模块数的增加会带来元件参数选取复杂的问题。
模块化多电平DC/DC 变换器(modular multilevel DC/DC converter,MMC-DC/DC)拓展灵活,可靠性高,适用于海上风电场等高压大容量的场合[9-10]。MMC-DC/DC 按是否具有变压器可分为隔离型[11-12]与非隔离型[13-16]。文献[11]设计了一种面对面式(front-to-front,FTF)的MMC-DC/DC,通过交流变压器将左右两侧模块化多电平换流器(MMC)连接起来,但变换器主要依靠交流变压器升压,且采用的方波调制使交流变压器两侧的电压变化率du/dt值较大,交流变压器参数设计困难。文献[12]设计了桥臂交替导通型MMC-DC/DC,在每个桥臂上多增加了切换开关,提高了故障隔离能力,但开关器件数量多,且器件均压困难。文献[13-14]提出了一种MMC 自耦型结构,省去了交流变压器,但无法实现电气隔离,同时桥臂上的交流分量也会显著增加系统损耗。文献[15-16]设计了容性能量转移型结构,成本、体积与重量均降低,但是仍然存在电气隔离能力欠缺的问题。因此,为使变换器具备较好的电气隔离能力,并降低系统损耗,本文考虑采用隔离型结构。
本文根据全直流海上风电大功率高压送出的特定需求,首先考虑电气隔离需求,结合模块化结构与MMC 的优点,提出一种复合模块化DC/DC 变换器拓扑;为提高变换器的升压比,提出基于双重移相的s/m调制策略,并针对该调制策略的特点改进了电容电压均衡控制方法;最后,通过MATLAB/Simulink 搭建模型进行验证。
1 高压送出DC/DC 变换器拓扑
文献[17]指出高压送出DC/DC 变换器有三大技术需求:大容量、高升压变比和故障隔离。为满足以上要求,本文将MMC 电路和模块组合型电路进行拓扑融合,形成一种复合模块化拓扑,如图1(a)所示。图1(a)中:UMV、UHV分别为中、高压侧的电压;IMV、IHV分别为中、高压侧的电流;UMV,i为模块i的中压输入电压;UHV,i为模块i的高压输出电压;uua,i、uub,i、ula,i、ulb,i与iua,i、iub,i、ila,i、ilb,i分别为模块i的桥臂电压与桥臂电流,下标u、l 分别表示上、下桥臂,a、b 分 别 表 示a、b 两 相;uuA,i、uuB,i、ulA,i、ulB,i与iuA,i、iuB,i、ilA,i、ilB,i分别为整流侧MMC 的上下桥臂电压与电流,下标A、B 分别表示A、B 两相;KT为隔离变压器的变比;ipi、isi与upi、usi分别为隔离变压器原、副边的电流与电压;Ls、Lp分别为整流MMC 与逆变MMC的桥臂电感。
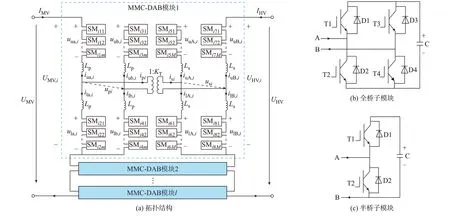
图1 高压送出DC/DC 变换器结构Fig.1 Structure of high-voltage output DC/DC converter
为实现变换器的高升压变比与故障隔离的目标,本文以隔离型结构为基础,同时为了充分利用MMC 调制策略所具备的升压功能(详见下文),以降低隔离变压器的升压压力、减小隔离变压器绝缘设计与制造难度,在隔离变压器两侧均采用MMC结构。此外,在实际应用中,风电场黑启动可能需要电网短时间提供功率,变换器需要具有一定的双向传输能力,相较于单有源桥(single active bridg,SAB)型电路,DAB 型DC/DC 变换器控制灵活,功率传输效率高,当DAB 与MMC 结合后,在高压侧短路时故障电流波及范围小,运行可靠性高,故本文对DAB 电路进行升级改造,用MMC 子模块串联式桥臂代替传统两电平桥臂,从而形成单相MMC 型DAB(MMC-DAB)电路模块,作为DC/DC 变换器的内层结构。在此基础上,通过采用输入串联输出串联(input-series output-series,ISOS)的结构,将多个MMC-DAB 模块进行组合输入串联、输出串联,作为变换器的外层结构,形成具有双层模块化复合结构特点的海上风电场高压送出DC/DC 变换器拓扑。
采用复合模块化拓扑的优势是,MMC-DAB 模块通过采用MMC 结构提高了单个DAB 电路模块的电压水平和功率等级,而多个模块通过串并联可以进一步提升电压或电流等级,适应不同的功率水平,以类似于“积木”的方式提供强大的灵活性,具有突出的模块化和可配置性特点。限于篇幅,本文着重分析ISOS 结构,该结构可以降低单个MMCDAB 模块的输入电压,减少了子模块数量。
图1(a)所示的MMC-DAB 模块中,逆变MMC的子模块采用全桥结构,如图1(b)所示,整流MMC采用半桥子模块,如图1(c)所示,对于两侧MMC 子模块类型选取不同的原因将在下文介绍调制策略时说明。两侧MMC 经过变比为KT的中频变压器连接和隔离,需要指出的是,由于需在海上换流站中安装,为减小DC/DC 变换器体积,交流变压器的工作频率要提升至上百赫兹甚至上千赫兹。文献[11,18]提出MMC 型大功率DC/DC 变换器采用一个集中隔离变压器实现隔离,但大容量的中高频变压器还在研究阶段,且变压器原副边电压相差较大。因此,无论是从功率等级还是绝缘水平方面,变压器的设计都面临极大的困难。
本文通过将多个MMC-DAB 模块进行串并联,以“化整为零”的方式降低了对中频变压器容量和变比的要求,从而规避了中频隔离变压器因高功率密度结构下的高压绝缘难题而造成的技术瓶颈,可充分借鉴现有成熟技术,满足高压大容量直流变换需求。
2 MMC-DAB 模块的调制策略与功率特性
2.1 基于双重移相的s/m 调制策略
海上高压送出DC/DC 变换器的主要任务是完成从中压侧到高压直流输电线路的电压变换以及海上风电场功率外送,对隔离变压器两侧电流、电压波形无须要求为标准正弦波,且相较于正弦波调制,方波调制下的直流电压利用率高、功率传输能力强[19]。为使MMC 具备升压功能,降低隔离变压器体积与制造难度,实现变换器大幅升压的目标,本文基于方波调制并借鉴DAB 的双重移相调制,提出了基于双重移相的s/m调制策略。
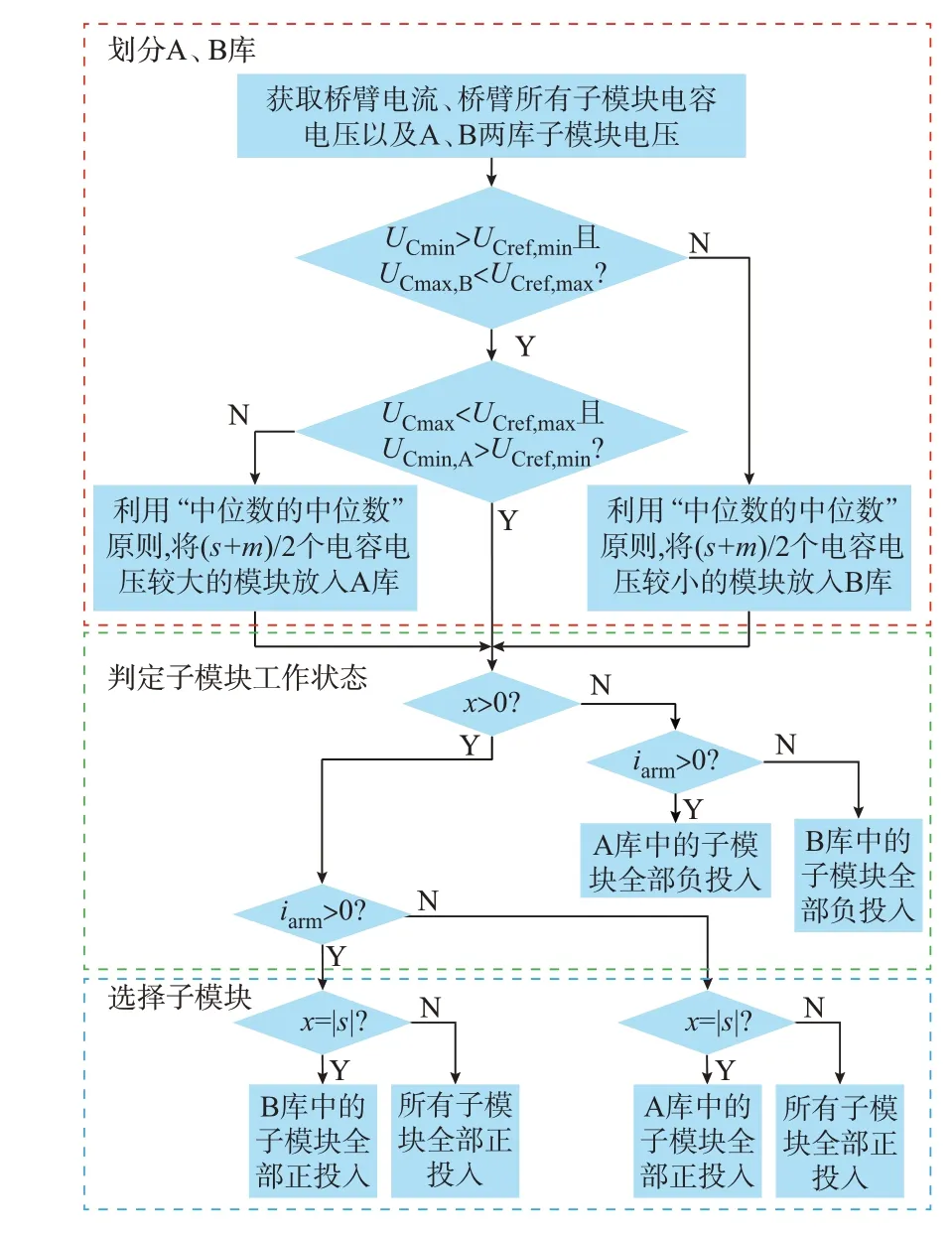
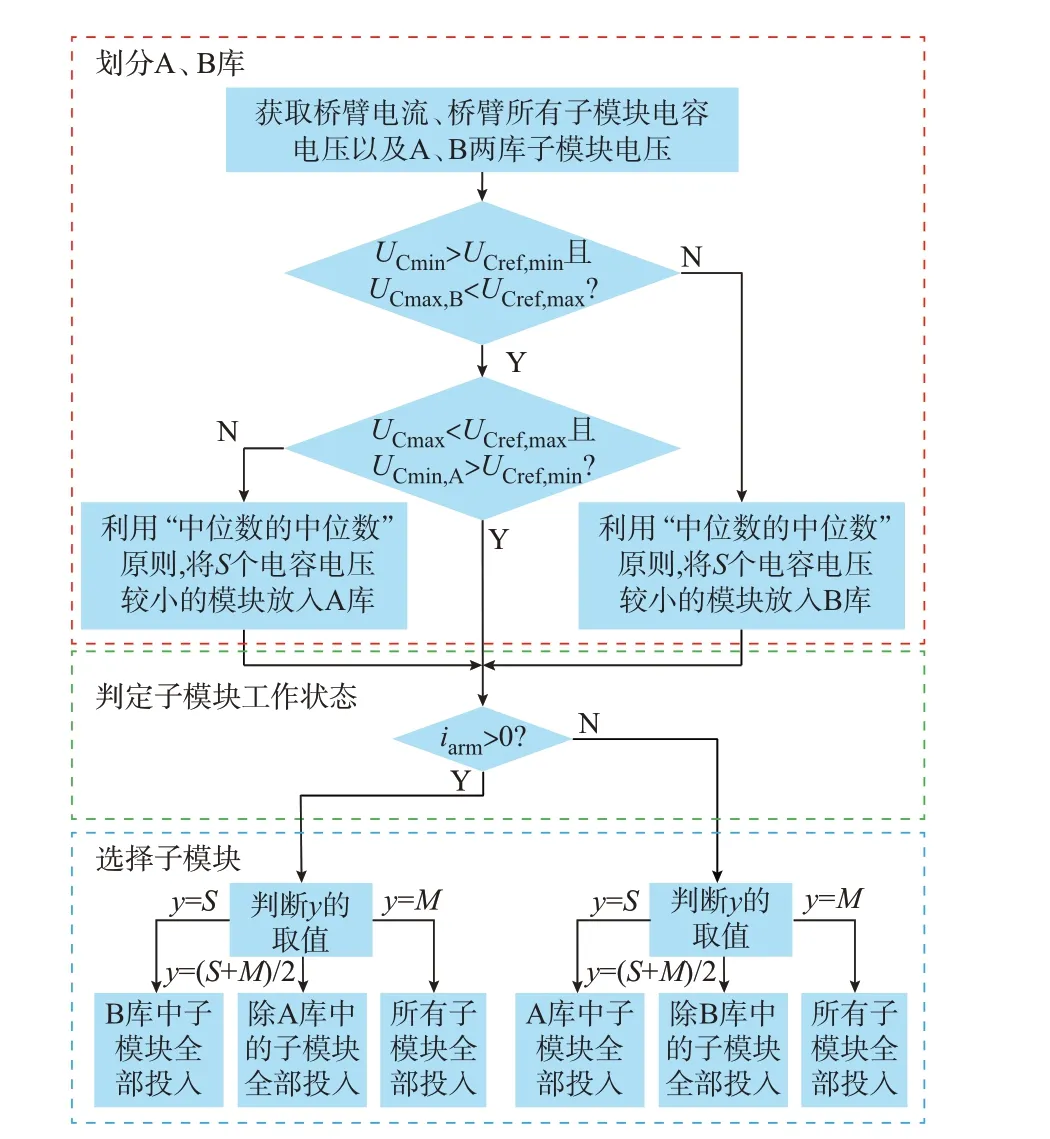
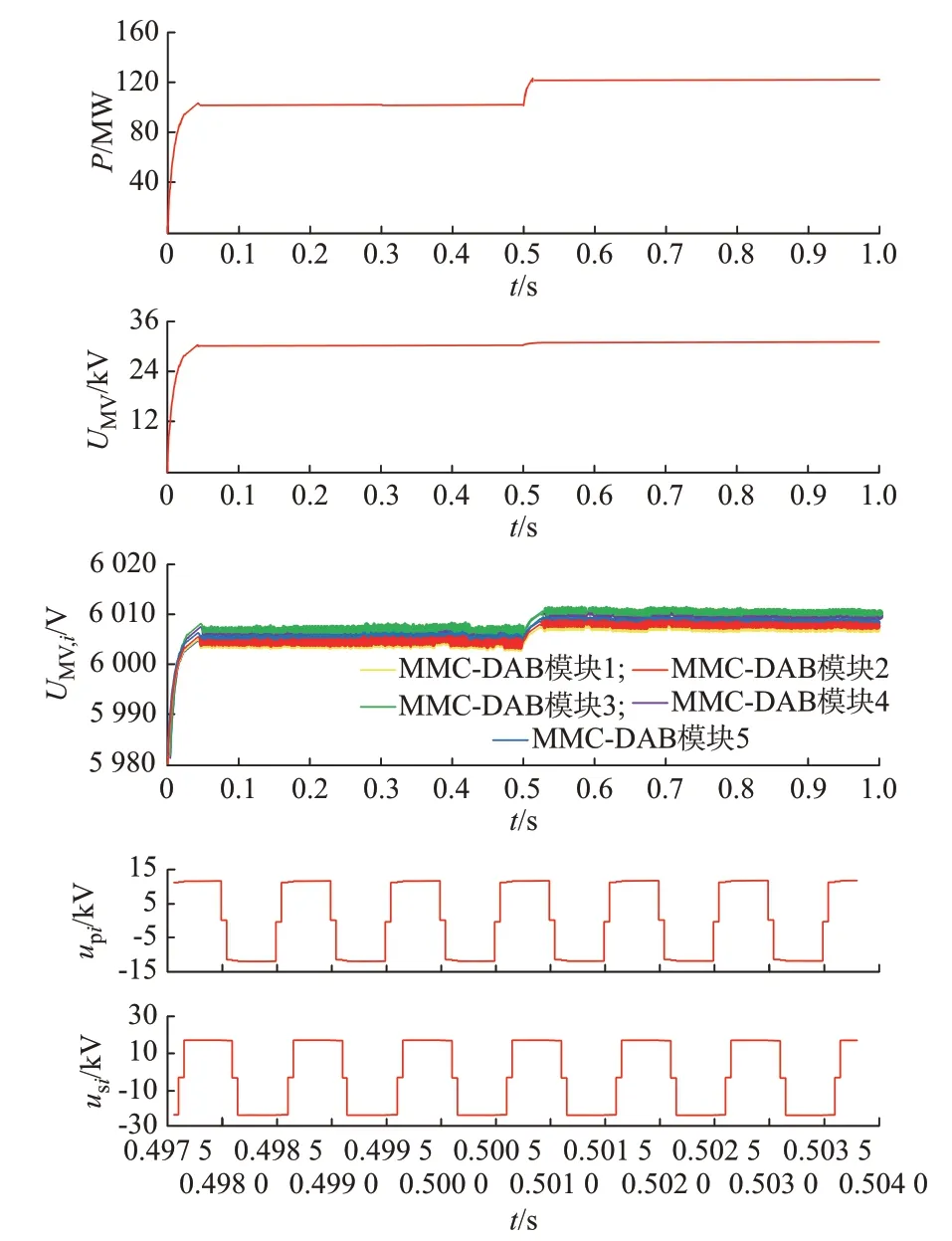
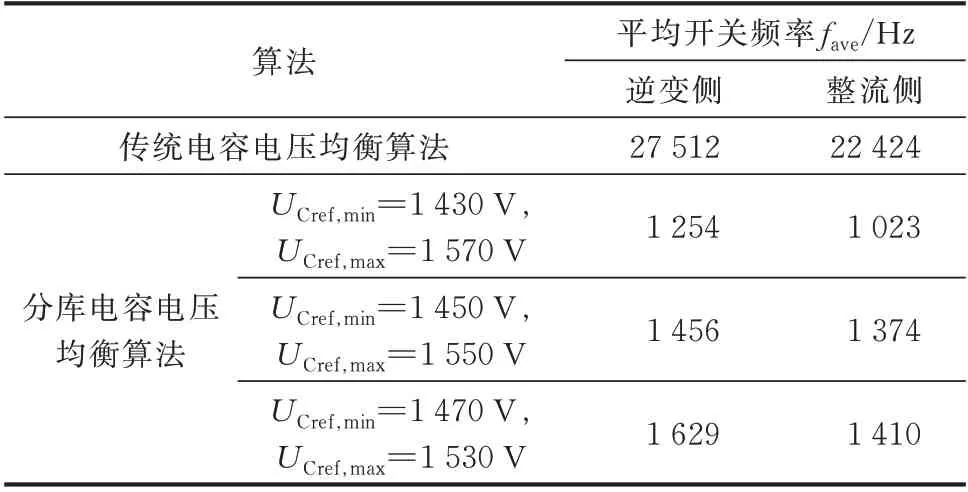
本文提出的s/m调制是指在上半个周期内上、下桥臂分别投入s、m个子模块,在下半个周期内上、下桥臂投入的子模块数交换。s与m都是固定值,代表一个桥臂可能投入的子模块数,规定s 现以图1 中第i个模块的逆变MMC 为例分析该调制策略的升压原理。假设在前半个周期内a 相上、下桥臂分别投入s、m个模块,b 相上、下桥臂分别投入m、s个子模块,则upi为: 式中:UC为子模块电容电压。 MMC 最基本的特征是上、下桥臂的子模块电压之和必须等于MMC 直流电压,即 由式(3)可以看出,为了使逆变MMC 的变比Ki,MMC>1,需使|m-s|>m+s,则需在逆变MMC 中采用具有“负投入”状态的全桥子模块,使s取负值。 同理,整流MMC 在前半个周期内,A 相上、下桥臂分别投入S、M个模块,B 相的上、下桥臂投入M、S个子模块,隔离变压器副边交流电压幅值Usi与UHV,i的比值为: 由式(4)可以看出,整流MMC 的子模块无需负投入便可实现升压功能,为减小器件的数量以及变换器体积,整流MMC 采用半桥子模块。 图1 中隔离变压器的变比为KT,结合式(3)与式(4),可得MMC-DAB 模块输出与输入电压的比值为: 由上式可知,MMC-DAB 模块的整体升压比由Ki,MMC、Kr,MMC以 及KT共 同 贡 献,s/m调 制 策 略 赋 予了MMC 升压功能,从而减少了对变压器变比的要求,变压器两侧电压差的减小使其绝缘设计与制造难度减小,对于高变比变换器的实现具有现实意义。 但s/m调制是一种两电平调制,隔离变压器两侧du/dt较大,增加了变压器绝缘压力,为此考虑将s/m调制与双重移相调制结合,以增加两侧MMC 交流电压的电平数。当某桥臂投入的子模块数在s(S)、m(M)之间周期性变换时,该桥臂将产生sUC与mUC(SUC与MUC)两种电平,由于每个桥臂中都含有多个子模块,当桥臂电压在sUC与mUC(SUC与MUC)之间跳变时,可以通过使桥臂投入子模块数为k(K)(s 图2 基于双重移相的s/m 调制下的电压波形Fig.2 Voltage waveforms with s/m modulation based on double phase shift 由于上、下桥臂投入子模块总数之和需满足式(2),且上、下桥臂在过渡电平期间投入的子模块数同时切换为K(k),因此K(k)的取值只能为(M+S)/2[(m+s)/2],此时隔离变压器副边电压为三电平阶梯波。 K个子模块投入时间所对应的角度为MMCDAB 模块整流MMC 内部的移相角θ,效果上类似于在DAB 电路中采用双重移相调制时,当控制H 桥内两桥臂之间的移相角时DAB 电路的交流侧可产生三电平阶梯波。借鉴DAB 电路中对移相角的命名,称θ为内移相角,此为一重移相。另一重移相对应DAB 电路中变压器原、副边两侧电压波形的移相角,即MMC-DAB 模块中变压器原、副边阶梯波之间的移相角,称为外移相角ϕ,用以完成功率传输功能。 三电平阶梯波相较于直接采用s/m调制输出的方波而言可以降低变压器两侧du/dt,此外,电平数的增加使桥臂投入子模块数多样化,使子模块组合序列的充放电方式更加灵活,有利于实现MMC 的电容电压均衡控制。 高压送出DC/DC 变换器在正常工作时仅需将功率从中压侧传输到高压侧,功率单向传输,由DAB 变换器工作原理可知该情况对应外移相角ϕ>0,为简化分析仅讨论正常工作时ϕ>0 的情况。 首先,对图1 中MMC-DAB 模块进行化简等效,将隔离变压器原边电压、漏感以及桥臂电感归算到副边,得到附录A 图A1 所示等效电路图。为便于分析,不再区分具体MMC-DAB 模块,在下文对涉及的物理量省略下标i,用上标“'”表示归算量。 附录A 图A1 中,设隔离变压器归算到副边侧的漏感为LT,则有: 式中:Lk为等效电感。 当ϕ>0 时,按照θ与ϕ的关系,可分为3 种工作模式:0<ϕ<θ、θ<ϕ<π-θ与π-θ<ϕ<π。各模式下经归算后得到隔离变压器原副边的等效电压、电感电压以及电感电流如附录A 图A2 所示。图A2 中,归算后隔离变压器原边电压u'p仍为三电平阶梯波,取值为U'ab、0 与-U'ab,隔离变压器副边侧电压us为UAB、0 与-UAB构成的三电平阶梯波,结合式(3)与式(4)可得归算后变压器原边与副边三电平阶梯波幅值U'ab与UAB为: 式中:Uab为归算前隔离变压器原边三电平阶梯波的峰值。 目前MMC 桥臂子模块的个数常设置为偶数,因此一般情况下逆变MMC 与整流MMC 升压比均可达到2,即Kr,MMCKi,MMC=4,大大降低了隔离变压器的升压压力。同时,在MMC 升压比为2 时,桥臂投入的3 种子模块数(m、s、k或M、S、K)也有特殊的 联 系 :假 设m+s=n,M+S=N,其 中n=UMV,i/UC、N=UHV,i/UC分别为在相同直流母线电压等级以及传统调制策略下,不考虑模块冗余时整流与逆变MMC 各桥臂子模块数量的理论设计值,当Kr,MMC=2、Ki,MMC=2 时,结合式(3)和式(4),有m=(3/2)n,s=-(1/2)n,M=(3/4)N,S=(1/4)N,故s=-k,S+K=M,上述关系在下文的电容电压均衡算法中也将用到。 通过上述分析可知,逆变MMC 各桥臂中全桥子模块总数m比传统调制下的理论值n多1/2,而整流MMC 各桥臂半桥子模块总数M比N少1/4。由于中、高压两侧直流电压水平的差异,N远大于n,同时相比于文献[11]中采用的三相结构的FTFMMC,本文提出的MMC-DAB 模块桥臂个数减少,故总体而言本文调制策略下子模块总数减少。 虽然逆变MMC 采用了全桥子模块,增加了器件使用数量,但逆变MMC 具备了升压功能,中频变压器的升压比降低,匝数比减小,有利于减少变换器整体体积。此外,全桥子模块具有故障隔离的能力,相较于文献[11]中采用在中频变压器两侧安装交流断路器以隔离故障的方式,本文采用全桥子模块可省去断路器。文献[7]中提到了DAB 模块组合型结构,由于各DAB 模块端口上设置了集中电容,当系统发生直流故障时,电容会迅速放电,故障电流增加,且当单个DAB 模块发生故障时,无法通过设置冗余模块代替故障模块运行,否则会使电容短路。但本文提出的拓扑由于采用了全桥子模块,不仅可以通过闭锁子模块阻断故障电流,而且当某个子模块故障时,可通过设置冗余子模块代替其运行,提高了变换器运行可靠性。因此,在逆变MMC 采用全桥子模块具有较好的应用前景。 假设电压传输比G=KTUab/UAB=U'ab/UAB,中频变压器的频率为f(角频率ω=2πf),随时间变化的角度(相角)φ=ωt。同时,在整流、逆变MMC 升压比均为2 时,隔离变压器原、副边三电平阶梯波的幅值分别为U'ab=2KTUMV,i、UAB=UHV,i/2。根据附录A 图A2 可求出0<ϕ<θ、θ<ϕ<π-θ与π-θ<ϕ<π 这3 种工作模式下的等效电感电流iLk的表达式,分别如式(8)—式(10)所示,以附录A 图A2(b)为例,iLk的推导过程见附录B。 将式(8)—式(10)中iLk的表达式代入式(11),得到不同工作模式下MMC-DAB 模块的传输功率,如式(12)所示。 由式(12)可知,由于电压传输比G与变压器的变比有关,由工程参数决定,故MMC-DAB 模块传输功率与θ以及ϕ有关。其中θ不能过小,由附录A图A2 可知,θ减小会导致电感电流增加,从而增加系统损耗,但也不能过大,否则会降低变换器的最大输出功率,因此通常将θ设定在一个合适的值(一般在0.1π 左右[20]),通过改变ϕ来调整变换器传输功率。由于θ较小,所以在θ<ϕ<π-θ的工作模式下ϕ调整空间大,允许的传输功率变化范围也较大,因此尽可能保证变换器运行在该工作模式下。 无论是半桥型MMC 还是全桥型MMC,传统电容电压均衡算法的核心都是判断子模块电容的充放电状态并找出电容电压第a小或第a大的子模块(记其电容电压值为UCa)。图1(b)、(c)为本文MMC 中所用的两种子模块类型,规定桥臂电流从图1 所示子模块的端口A 流进、端口B 流出时电流方向为正,反之为负,得到在不同子模块类型输出电平与桥臂电流方向变化时子模块电容的充放电状态,如附录A 表A1 所示。但传统算法需要对桥臂上所有子模块电容电压进行有序排列,存在计算量增加的问题,为此引入“中位数的中位数”选择算法:首先,选取枢纽元[21],接着对所有电容电压进行划分以及递归调用,从而寻找UCa,具体步骤见附录C。根据文献[22-23]可知,采用冒泡算法、快速排序算法以及“中位数的中位数”原则选取UCa时,比较次数与模块个数M的 关 系 分 别 为C1(M)≈0.5M2、C2(M)≈1.44Mlog2M、C3(M)≈1.9M,对比发现随着子模块数的增加,由于本文采用的算法无须进行有序排列,计算量大大降低。 电容电压均衡控制算法的设计需要与调制策略的特点相结合,本文采用的s/m调制策略最大的特点是桥臂投入的子模块数只有s(S)、m(M)、k(K)这3 种情况,特别是根据2.2 节的分析可知,当两侧MMC 的 升 压 比2 时,在 逆 变MMC 中k=-s,整 流MMC 中K=2S。若不考虑子模块的冗余,当桥臂所需投入子模块数为m(M)时投入所有子模块,无须进行排序与筛选,仅在桥臂投入s(S)、k(K)个子模块时考虑电容电压均衡问题。 由于全桥子模块输出电平有3 种情况,因此逆变MMC 在确定桥臂所需投入电平数后,桥臂子模块的组合投入方式相较于整流MMC 更加灵活,但器件的动作状态随之变得复杂。为减少桥臂投入子模块数跳变时开关动作的器件数量,降低开关损耗,本文在确定逆变MMC 桥臂投入子模块数量时,考虑单个桥臂上子模块只有正投入组合或负投入组合状态,而不考虑包括正、负投入的混合组合状态。 对于逆变MMC,由于s与k互为相反数,即除去桥臂子模块全部投入的情况,无论桥臂子模块需要正投入还是负投入,投入的数量都是一致的,均为|s|。由附录A 表A1 分析可知,可以通过桥臂电流的方向以及子模块输出电平判断电容充放电状态:充电时需要投入电容电压最小的|s|个全桥子模块,反之需要投入电容电压最大的|s|个全桥子模块。需要投入的子模块内部的器件状态取决于模块的投入模式(正投入或负投入)。 由上述分析可知,通过将子模块分为两大组(充电组与放电组)并判断子模块充放电状态便可确定各子模块的投入状态,因此本文提出了分库电容电压均衡算法。针对全桥型MMC 分库电容电压均衡算法的流程如图3 所示:利用“中位数的中位数”原则对各桥臂上的m个子模块进行分库,分为电容电压较大A 库与电容电压较小B 库,两库中的元素数量均为|s|;当子模块电容需要放电时投入A 库,充电时投入B 库;在电容电压波动允许的范围内两库内元素不变,以保证在子模块充放电状态变化前各子模块的投入状态不变,从而降低开关次数,一旦电压波动范围超过允许值则按要求重新分库。 图3 中,x表示逆变MMC 桥臂所需投入模块数(x=s、k、m),iarm表示桥臂电流,UCmin、UCmax分别为实际运行中桥臂所有子模块电容电压的最小值与最大值,UCmin,A、UCmax,B分别为A 库中电容电压的最小值与B 库中电容电压的最大值,UCref,max、UCref,min分别为理论设定的电容电压最大与最小的允许值,并在运行中要求UCmin>UCref,min,UCmax 图3 全桥型MMC 分库电容电压均衡算法流程Fig.3 Flow chart of partition-database capacitor voltage balancing algorithm for full-bridge MMC 为进一步控制电容电压波动在允许的范围内,除需检测UCmin与UCmax外,还要关注库内电压的范围,由于A 库中电容将工作于放电状态,因此只需对该库中的最小值UCmin,A进行判断,同理对于B 库仅需关注其中的最大值UCmax,B。 对于整流MMC,由于半桥子模块没有负投入的状态,仅需判断桥臂电流的方向即可判断子模块电容的充放电状态。 在整流MMC 中,由于在投入S与K个子模块时,桥臂投入的子模块数量不同,故不能直接将某个库全部投入,但为了充分利用分库的优势,仍将各桥臂上的子模块分为A、B 两个库,库中元素个数均为S,当桥臂所需投入模块数y=S时,根据充放电状态将某库全部投入,当y=K=(S+M)/2 时,由2.2 节可知,Kr,MMC=2 时有y=M-S,据此可方便选择需要投入的子模块:需要充电时,将用来放电的A 库的子模块闭锁,其他子模块全部投入;反之闭锁B库,其他子模块全部投入。上述电容电压均衡算法流程如图4 所示,图中y表示整流MMC 桥臂所需投入子模块数,其他变量含义与图3 相同。 图4 半桥型MMC 分库电容电压均衡算法流程Fig.4 Flow chart of partition-database capacitor voltage balancing algorithm for half-bridge MMC 综上,分库电容电压均衡算法流程分为3 个步骤:1)划分A、B 两库;2)对子模块工作状态进行判定;3)选择投入的子模块。由前述可知,该算法与本文提出的拓扑和调制策略高度适配,不仅减小了计算量,还降低了器件的开关次数。 在附录A 图A3 所示的两级升压海上直流风电场中,需要对低、中、高3 个直流环节的电压进行稳定控制,分别由中压汇集DC/DC 变换器、高压送出DC/DC 变换器以及岸上换流站实现。 由于本文DC/DC 变换器采用ISOS 结构,故在设计变换器的控制策略时,不仅需要保证中压输入侧的电压稳定,还需考虑各MMC-DAB 模块的均压问题。由文献[24]可知,若能保证各模块输入均压,输出电压将自动平均分配,则各模块的输入电压有: 式中:l为DC/DC 变换器中MMC-DAB 模块的数量。 将定中压控制与输入均压控制相结合,提出了如附录A 图A4 所示的高压送出DC/DC 变换器控制策略。定中压控制采用双闭环结构输出外移相角ϕ,与输入均压控制得到的外移相角修正量Δϕ1,Δϕ2,…,Δϕl作 差,得 到 各 模 块 的 外 移 相 角ϕ1,ϕ2,…,ϕl,经过调制与电容电压均衡控制产生各器件的触发信号,实现高压送出DC/DC 变换器的稳定控制。 为验证本文所提出的基于MMC-DAB 模块的ISOS 型高压送出DC/DC 变换器的拓扑结构、调制与控制策略的可行性,在MATLAB/Simulink 中搭建了如图1 所示的变换器仿真模型,中压侧电压设置为30 kV,高压侧为300 kV,额定容量为100 MW,整个变换器由5 个MMC-DAB 模块串联组成,单个模块的仿真参数如附录A 表A2 所示。 为验证定电压控制策略的有效性,在0.5 s 时令变换器传输功率由100 MW 跃变至120 MW,其传输功率P、中压侧电压、各MMC-DAB 模块输入电压以及隔离变压器原、副边电压仿真波形如图5所示。 图5 DC/DC 变换器仿真波形Fig.5 Simulation waveforms of DC/DC converter 从图5 中可以看到,当DC/DC 变换器传输功率变化时,中压侧电压UMV与各MMC-DAB 模块输入电压波动较小,且5 个模块的输入电压也保持了较好的一致性。隔离变压器原边电压upi为由12 kV、0 kV、-12 kV 构成的三电平阶梯波,逆变MMC 实现了从中压侧到变压器原边1∶2 的升压比,同理整流MMC 也实现了1∶2 的升压,验证了本文提出的基于双重移相的s/m调制具有升压的功能。 为了验证本文所提出的分库电容电压均衡算法对于降低开关频率的作用,将其与传统均衡算法进行比较,传统算法下子模块的开关状态与电容电压波动情况如附录A 图A5 所示。 当采用分库均衡算法,设置UCref,min=1 430 V、UCref,max=1 570 V 和UCref,min=1 470 V、UCref,max=1 530 V 两种情况,子模块电容电压波动与器件开关状态分别如附录A 图A6、图A7 所示。对比图A5—图A7 可知,传统算法下子模块在0.000 5 s 内开关状态就要改变40 次左右,实际工程中器件难以承受如此高的开关频率,故其不适用于本文提出的调制策略。在分库均衡算法下,子模块的触发脉冲几乎与隔离变压器的工作频率一致,虽然电容电压的一致性稍逊传统算法,但电压波动范围都在5%的允许范围内,且随着电容电压上、下限参考值范围的缩小,其波动范围减小,一致性得到提高。 为量化分析,引入平均开关频率fave,以逆变MMC 为例,fave=Ncut,off/m,Ncut,off表示单位时间内某一桥臂上所有器件开通与关断的次数总和,采用不同电容电压均衡算法下fave统计结果如表1 所示。 表1 不同算法下器件的平均开关频率Table 1 Average switching frequency of devices with different algorithms 从表1 可以看出,在分库电容电压均衡算法下器件的平均开关频率下降到隔离变压器工作频率附近,而传统算法下开关频率达到数十千赫兹。虽然在分库电容电压算法下子模块电容电压一致性稍逊传统算法,但综合考虑器件开关频率、损耗以及电压波动范围,本文采用的分库电容电压均衡算法具有较大的优势。 本文结合全直流海上风电场对大容量高压送出DC/DC 变换器的技术需求,提出了基于MMCDAB 模块ISOS 的复合模块化DC/DC 变换器拓扑,得到如下结论: 1)本文提出的基于MMC-DAB 模块的复合模块化变换器结构,增加了拓扑灵活性和对不同电压水平或功率等级的适应性,尤其适用于海上风电送出等大功率、高电压应用场合,同时中频变压器额定容量减少,原、副边电压绝缘要求下降,大大降低了工程实现难度; 2)提出的基于双重移相的s/m调制策略,配合逆变侧MMC 和整流侧MMC 桥臂全桥和半桥子模块选型,赋予了变换器升压功能,减小了隔离变压器升压的压力; 3)结合调制特点提出的分库电容电压均衡算法,可在保持电容电压在允许范围内波动的同时显著降低开关频率,减少开关损耗,计算量也大大减小。 本文主要目的是为海上直流风电场的高压送出DC/DC 变换器提供一种方案,侧重于理论创新性研究,但还未开展实验研究和验证。此外,本文主要考虑了变换器稳态运行情况下的控制策略,为保证当系统或变换器内部发生故障时DC/DC 变换器的安全与可靠运行,需进一步研究故障电流的限制及阻断方法。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

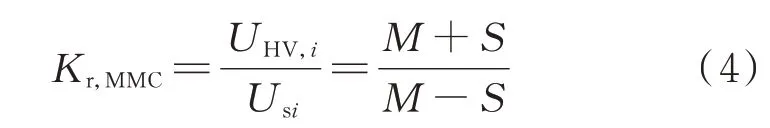
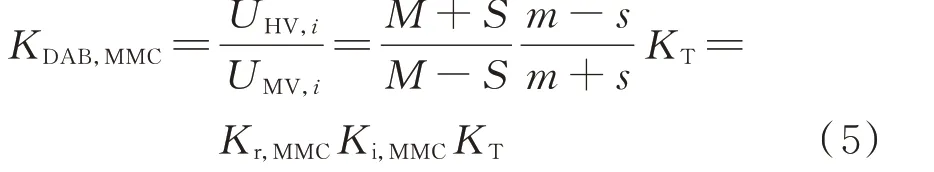
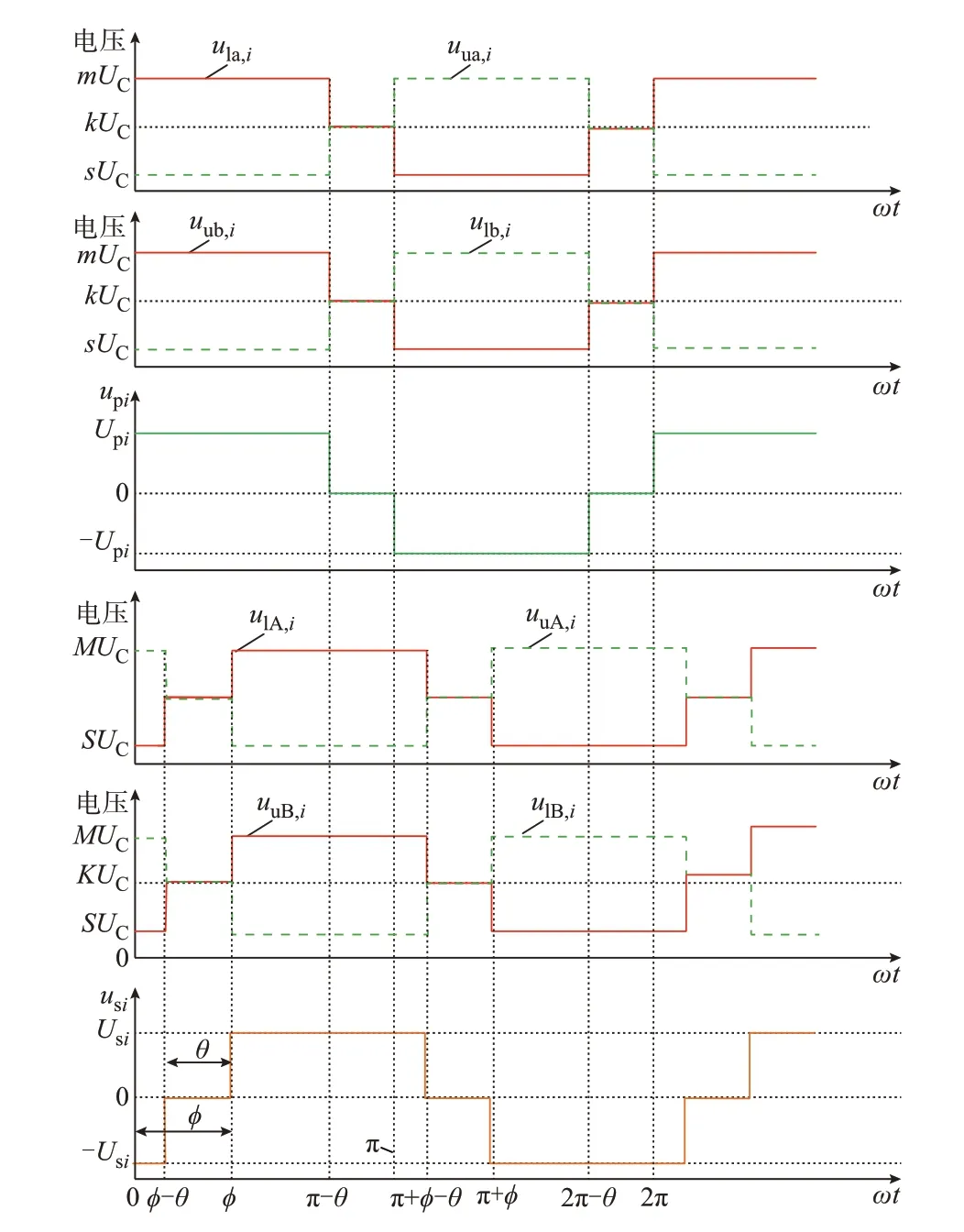
2.2 功率传输特性分析
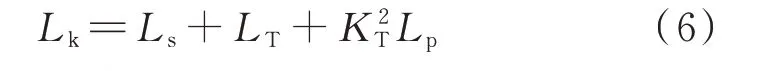
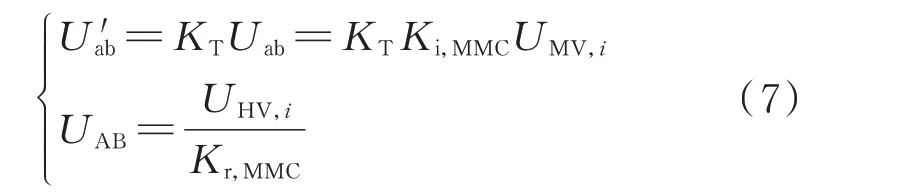

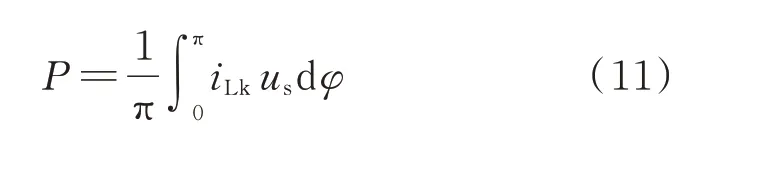
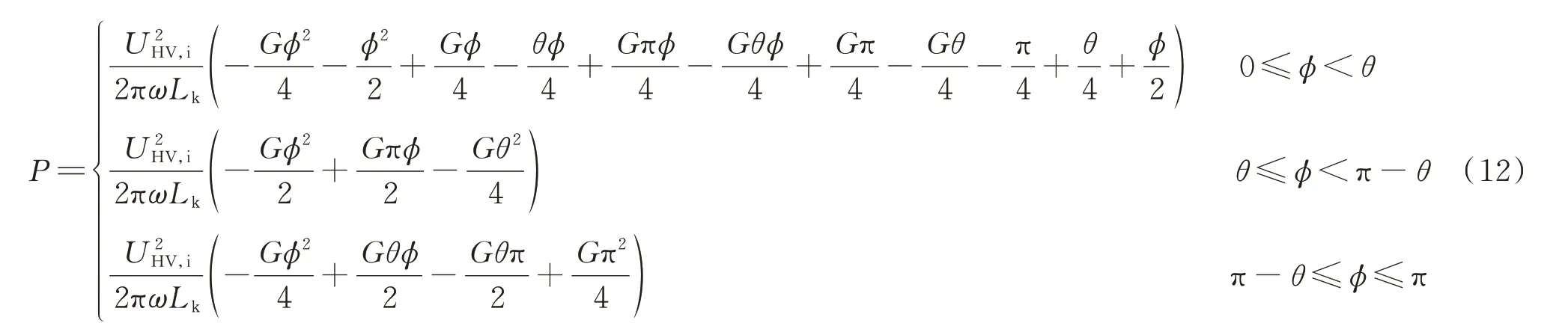
3 电容电压均衡与定电压控制策略
3.1 分库电容电压均衡算法
3.2 定电压控制策略
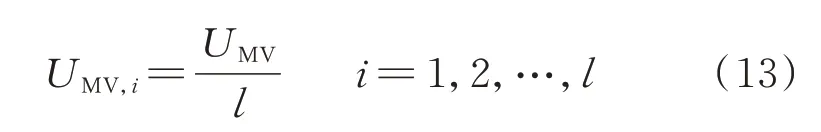
4 仿真验证
5 结语
