光伏与LCC-HVDC 系统的次同步振荡耦合路径及阻尼特性分析
2022-02-02高本锋陈淑平
高本锋,陈淑平,刘 毅
(1. 河北省分布式储能与微网重点实验室(华北电力大学),河北省保定市 071003;2. 国网山东省电力公司枣庄供电公司,山东省枣庄市 277100;3. 国网江苏省电力有限公司苏州供电分公司,江苏省苏州市 215000)
0 引言
随着“双碳”目标的提出,中国光伏发电进入大规模发展阶段。同时,考虑到电网换相型高压直流(line-commutated-converter based high voltage direct current,LCC-HVDC)系统大容量、远距离送电的优势,LCC-HVDC 系统成为光伏外送的重要方式,其中“三北”地区的大规模光伏主要经LCC-HVDC 系统外送[1-2]。
现有研究表明,光伏自身存在弱阻尼的次同步振荡(sub-synchronous oscillation,SSO)问题[3]。随着中国“三北”地区光伏经LCC-HVDC 系统外送(photovoltaic stations via LCC-HVDC,PVSL)工程相继投运,LCC-HVDC 系统送端近区的光伏容量持续增加,其振荡稳定性问题更加凸显[4],光伏和LCC-HVDC 系统的次同步交互作用可能成为引发系统SSO 的因素之一[5]。针对光伏与LCC-HVDC系统间电气距离较小的场景,光伏与LCC-HVDC系统的次同步交互作用更为明显。这种交互作用可能会削弱SSO 模态阻尼,使系统SSO 的风险增加。因此当光伏位于LCC-HVDC 系统近区时,两者的动态交互作用不可忽视,对此场景开展相关研究具有实际工程价值。
目前,针对光伏外送系统SSO 问题的研究,多集中于光伏并入弱交流电网、光伏与其他能源打捆外送的场景,较少涉及PVSL 系统。文献[6-7]研究表明光伏并入弱交流电网时存在发生SSO 的风险。文献[8-9]分别采用阻抗分析法和特征值分析法分析光伏并网时的SSO 特性。文献[10]分析了光火打捆外送时光伏对系统SSO 特性的影响,表明光伏并网有可能削弱部分频率点阻尼。文献[11]表明当光伏光照强度、逆变器控制参数变化时,可能导致风光混合电场并网系统发生SSO。上述文献的研究结论对PVSL 系统SSO 问题的指导意义有限,LCC-HVDC 系统投运对光伏SSO 的影响尚无明晰的结论。因此,亟须通过合适的方法,开展光伏与LCC-HVDC 系统的次同步交互作用研究。
对新能源并网系统进行SSO 分析时,现有文献多采用特征值分析、阻抗分析和时域仿真等方法[12]。特征值分析法能够准确提供系统的特征信息[13],广泛应用于传统电力系统与新能源并网系统的SSO 分析中[14-16]。但该方法物理意义不够明确,缺乏对系统内部各控制器间作用环路的合理描述。阻抗分析法采用阻抗模型表征系统受到扰动时的外特性[12],基于阻抗稳定判据判别稳定性[17-19]。虽具有明确的物理意义,但通常是以聚合阻抗表征实际系统,难以揭示扰动在系统内部的传递过程[20]。时域仿真法常用于验证其他方法的有效性[21],无法深入揭示耦合机理。鉴于上述方法的局限性,需要寻找新的方法,对PVSL 系统的振荡耦合路径及次同步交互作用机理进行分析。
本文拟采用闭环传递函数模型分析PVSL 系统的振荡耦合路径,提出一种阻尼分离方法,研究次同步交互作用对PVSL 系统的影响。该方法的主要优势如下:1)采用闭环传递函数框图(后称“框图”)分析PVSL 系统的交互作用,能够清晰展现系统的振荡耦合路径,直观揭示系统SSO 模态阻尼的形成过程;2)将阻尼转矩法[21-22]推广至SSO 模态的阻尼特性分析,通过重新构建框图实现阻尼分离,有效提取各振荡耦合路径阻尼,量化交互作用对SSO 阻尼的影响。
光伏直流电容振荡模态在交流系统强度较弱时更易失稳[23-24],故本文选择直流电容振荡模态,进行PVSL 系统的次同步交互作用分析及阻尼特性研究。首先,构造出PVSL 系统框图,据此揭示PVSL系统的振荡耦合路径及次同步交互作用机理。然后,将同步发电机的阻尼转矩法应用于直流电容振荡模态,根据线性系统叠加原理,重构框图实现阻尼分离,量化各类交互作用对SSO 模态阻尼的影响。最后,基于上述阻尼分离法并结合时域仿真,进行PVSL 算例的阻尼特性和影响因素分析。
1 光伏经LCC-HVDC 外送系统
PVSL 系统的结构及其控制策略如图1 所示,主要参数如附录A 表A1 所示。图中:PLL 表示锁相环;PLLi 和PLLr 分别表示逆变站和整流站锁相环;PWM 表示脉宽调制;Udc、ut、ucf、ug、ucl分别为直流电容电压、逆变器端口三相电压、滤波器电容三相电压、网侧三相电压和并联电容三相电压;ipv、in、it、icf、ig、il分别为光伏阵列端口输出电流、直流侧电容输出电流、逆变器输出三相电流、滤波器电容三相电流、网侧电流和光伏电站输电线路电流;C为光伏电站直流侧电容;Cf、Lf1、Lf2分别为滤波器电容、电感;R1、R2、L1、L2、L0、Cb分别为线路电阻、电感、电容;uac1和iac1分别为送端交流系统三相电压及电流;ur、Udcr、ui、Udci分别为整流站母线三相电压及直流电压、逆变 站 母 线 三 相 电 压 及 直 流 电 压;ir、Idcr、ii、Idci分 别 为整流站线路三相电流及直流电流、逆变站线路三相电 流 及 直 流 电 流;Rdc、Ldc、Cdc分 别 为 直 流 输 电 线 路电阻、电感、电容;Rac1、Rac2、Lac1、Lac2分别为交流线路电阻、电感;uac2和iac2分别为受端交流系统三相电压及电流;θpll、θpllr、θplli分别为光伏侧、直流整流侧、直流逆变侧锁相环输出的角度;φur、φui、αr、αi分别为整流站、逆变站母线电压的相角及触发角指令值;γ为逆变站关断角;其余变量说明参见附录A 表A1 至表A3。此外,控制框图中,下标带有dq或者abc 的变量表示对应变量的dq及abc 分量,下标带有ref 的变量表示对应变量的参考值。
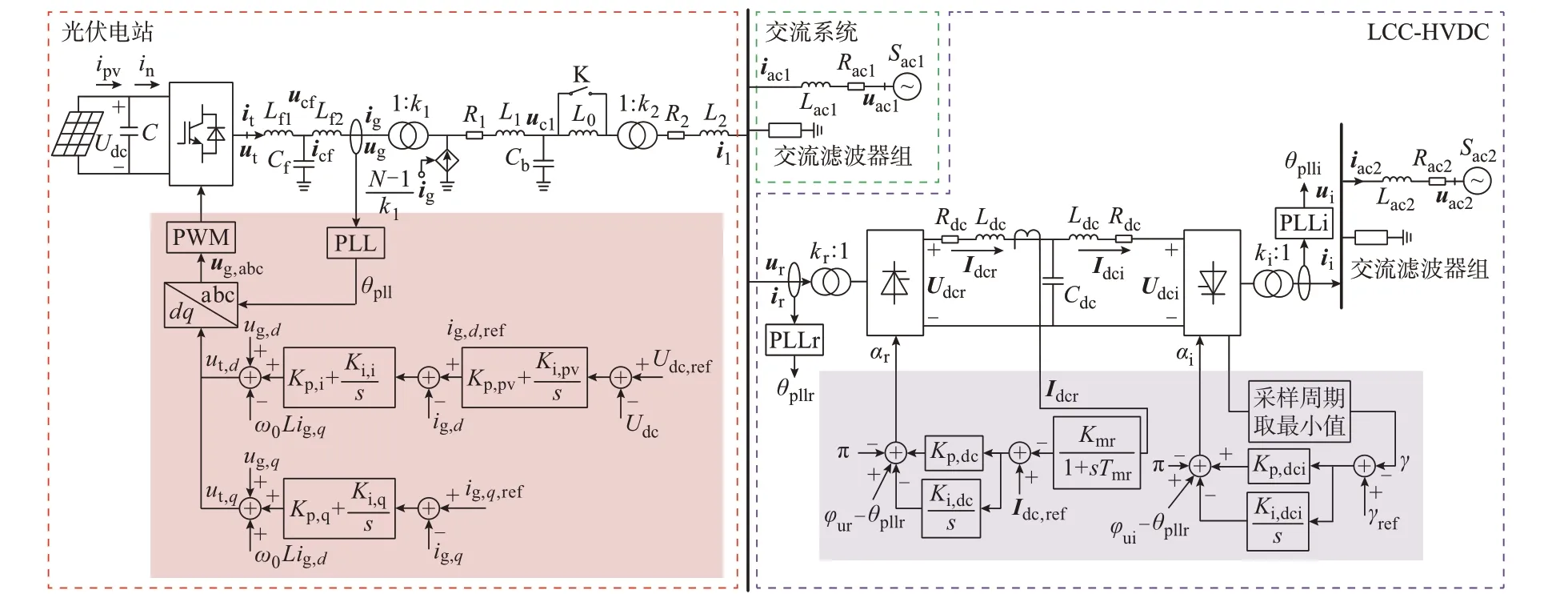
图1 PVSL 系统的结构示意图Fig.1 Schematic diagram of PVSL system structure
如图1 所示,为便于分析各子系统的交互作用,可将PVSL 系统分为光伏电站、LCC-HVDC 系统、交流系统三部分。当光伏并网系统发生SSO 时,光伏电站通常作为一个整体与电网发生交互作用[8,25-26],因此本系统光伏电站采用光伏发电单元的聚合等值模型。
本文所选取的研究系统算例中,光伏电站容量为200 MW,由多台型号相同的光伏发电单元聚合而成,辐照度和温度均采用标准工况对应值,其控制参数与运行状态均保持一致。考虑到实际工程中大规模光伏电站多采用结构简单、损耗较小、成本较低的单级式并网光伏发电系统结构[27],研究系统的并网光伏逆变器采用单级式拓扑,控制策略采用基于电网电压定向的矢量控制策略,其控制参数列于附录A 表A2。
LCC-HVDC 子系统包括LCC-HVDC 系统、受端交流系统及逆变站交流滤波器组。LCC-HVDC系统采用国际大电网会议提出的高压直流输电标准模型[28],其控制参数列于附录A 表A3。由于受端系统只与逆变站相连,对光伏与LCC-HVDC 系统的交互作用影响较小,故采用戴维南等值法[29]将受端交流系统简化为等值电压源(Sac2)及其等值阻抗(Rac2+jXac2)。
交流系统包括送端交流系统及整流站交流滤波器组。鉴于本文重点研究光伏与LCC-HVDC 系统的交互作用,PVSL 系统中光伏电站距整流站较近,而送端火电机组远离整流站,因此根据戴维南等值定理,将送端交流系统等效为等值电压源(Sac1)及其等值阻抗(Rac1+jXac1)。
2 PVSL 系统闭环传递函数模型
依照直流电压时间尺度运动方程的基本概念,本章分别建立光伏、LCC-HVDC 系统以及交流系统的线性化模型。整合各子系统端口,构建对应于图1 所示结构的PVSL 系统闭环传递函数模型,为后续次同步交互作用分析奠定理论基础。
2.1 各子系统线性化模型
PVSL 系统涉及3 种坐标系:光伏在dq坐标系下建模,交流系统在xy坐标系下建模,LCC-HVDC系统在极坐标系下建模。为便于进行各子系统接口的连接,光伏和LCC-HVDC 子系统接口处的变量需要转换至公共xy坐标系下。2 种坐标系与公共坐标系的转换关系如附录B 图B1 所示,x轴定向于交流系统电压矢量,dq旋转坐标系为光伏锁相环参考坐标系,θpll为dq坐标系与公共xy坐标系间的夹角,ρ、φ分别为LCC-HVDC 子系统中对应变量β的幅值与相角。变量α在dq坐标系与xy坐标系间的转换关系如附录B 式(B1)所示,变量β在极坐标系与xy坐标系间的转换关系如附录B 式(B2)所示。
在建立光伏线性化模型时,应保留关键惯性元件(即直流电容)状态变量,替换模型中间变量(并联电容电压、网侧电压、电流的xy分量),建立直流电压时间尺度下的线性化运动方程模型[30]。光伏线性化模型的具体推导过程如附录B 式(B3)至式(B20)所示,所构造的光伏线性化模型框图如附录B图B2 所示,图中已标注出各传递函数(矩阵)所属环节。由图B2 可知,光伏线性化模型的输入量为变量ur的xy分 量Δur,x、Δur,y,输 出 量 为 变 量il的xy分 量Δil,x、Δil,y。
针对本文所研究的直流电压控制时间尺度动态稳定问题,LCC-HVDC 系统的准稳态模型能够满足分析需要[4]。限于篇幅制,本节仅阐述整流站线性化过程,但实际分析中同时考虑了整流站、逆变站及受端交流系统。LCC-HVDC 系统传递函数表达式的具体推导过程如附录B 式(B21)至式(B31)所示,所构造的LCC-HVDC 系统线性化模型框图如附录B 图B3 所示,各传递函数(矩阵)所属环节均在图中标出。由图B3 可知,LCC-HVDC 系统线性化模型的 输 入 量 为Δur,x、Δur,y,输 出 量 为 变 量ir的xy分 量Δir,x、Δir,y。
交流系统包括等值电源及阻抗、整流侧交流滤波器组两部分,其具体推导过程如附录B 式(B32)至式(B35)所示,所构造的交流系统线性化模型的传递函数框图如附录B 图B4 所示。由图B4 可知,交流系统线性化模型的输 入量为Δil,x、Δil,y、Δir,x、Δir,y,输出量为Δur,x、Δur,y,能够与光伏、LCC-HVDC子系统的输入、输出量连接形成闭环传递函数模型。
2.2 闭环传递函数模型的准确性验证
连接上述各子系统形成PVSL 系统闭环传递函数模型,通过与时域仿真模型的阶跃响应曲线进行对比,验证所建模型的准确性。基于第1 章中的系统结构与运行参数,在PSCAD/EMTDC 时域仿真平台中搭建对应的电磁暂态仿真模型,并于5.0 s 时刻设置光伏直流电压指令值Udc,ref阶跃,阶跃幅值为0.05 kV,其他参考值保持不变。阶跃响应特性对比结果如图2 所示,图2(a)至(d)分别为光伏阵列输出电流Ipv、光伏直流电容电压Udc、网侧电流d轴分量Ig,d、LCC-HVDC 系统整流站直流电流Idcr的阶跃响应曲线。
由图2(a)至(d)可知,闭环传递函数模型与时域仿真模型的阶跃响应曲线结果基本一致,验证了闭环传递函数模型的准确性。
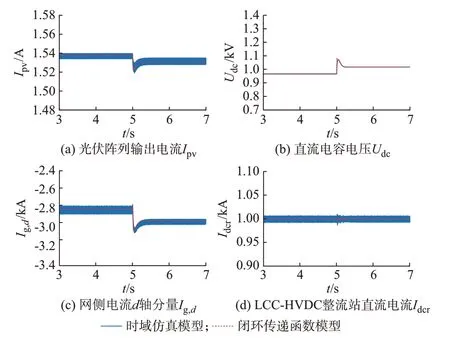
图2 阶跃响应曲线Fig.2 Step response curves
3 PVSL 系统振荡耦合路径及次同步交互作用分析
本章对第2 章构建的闭环传递函数模型进行整理,使其能够直观地体现阻尼路径的影响环节和路径之间的耦合关系,据此揭示PVSL 系统的振荡耦合路径及次同步交互作用机理,为后续第4 章的阻尼分离及第5 章的影响因素分析奠定基础。
鉴于分析重点为光伏与LCC-HVDC 系统间的次同步交互作用,而非装置内部的扰动传递过程。因此,构造PVSL 系统框图时,需对振荡元件外的环节(如逆变器、锁相环、换流单元、定电流控制器等环节)进行聚合处理,各子系统接口变量间的关系如式(1)至式(5)所示,聚合后的框图如图3 所示。
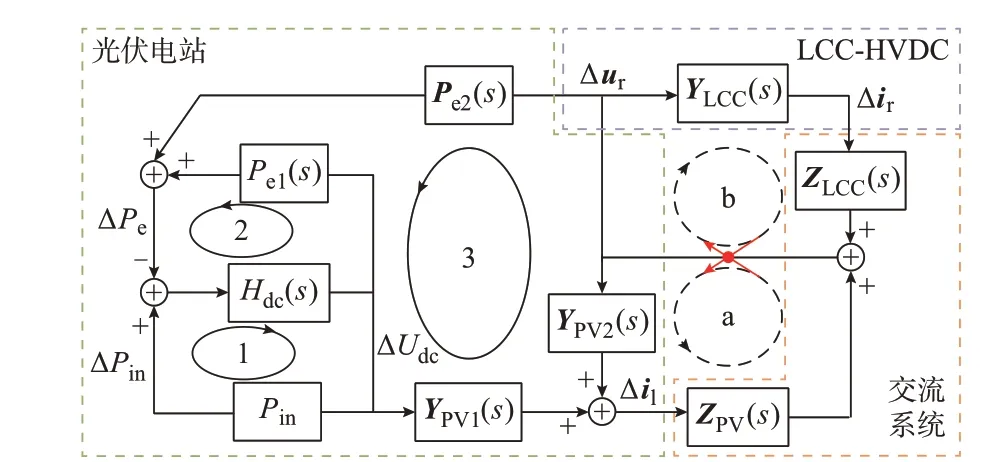
图3 PVSL 系统框图Fig.3 Block diagram of PVSL system
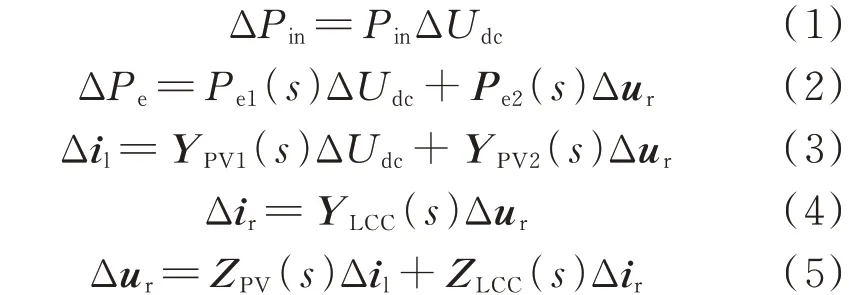
式 中:Pin、Pe1(s)、Pe2(s)、YPV1(s)、YPV2(s)、YLCC(s)、ZPV(s)、ZLCC(s)为各子系统状态变量间的开环传递函数(矩阵);ΔPin和ΔPe分别为直流电容环节输入功率和输出功率;Δ 表示对应变量的增量,下同。其中,式(1)至式(3)表征光伏电站中各变量间的开环传递函数关系,式(4)表征LCC-HVDC 系统中输入量与输出量间的开环传递函数关系,式(5)表征交流系统中输入量与输出量间的开环传递函数关系。
由图3 可知,PVSL 系统内包含3 条路径,均经过与直流电容主导SSO 模态相关的传递函数Hdc(s),为直流电容振荡模态的阻尼路径,分别用相应实线与虚线标出阻尼路径及其内部闭环回路,箭头方向表示次同步分量的传递方向,其中,阻尼路径1、2 仅在光伏内部形成,阻尼路径3 经过光伏、LCCHVDC 系统和交流系统,且在LCC-HVDC 系统和交流系统处存在由2 条闭环回路组成的闭合交叉环路。
阻尼路径1 具体可描述为:假定ΔPe保持不变,扰动由ΔUdc传递至ΔPin的通路。传递函数Hdc(s)、Pin共同构成了阻尼路径1,表明该路径与光伏直流电容环节、光伏输出特性系数有关。阻尼路径1 表征扰动在光伏阵列输入功率回路中的传递路径,故称其为输入功率振荡传递路径。
阻尼路径2 具体可描述为:假定ΔPin、Δur保持不变,扰动由ΔUdc传递至ΔPe的通路。传递函数Hdc(s)、Pe1(s)共同构成了阻尼路径2,表明该路径与光伏直流电容环节、逆变器控制有关。由式(2)可知,阻尼路径2 表示由ΔUdc至ΔPe的变量转换关系,表征扰动在部分电磁功率回路中的传递路径,故称其为电磁功率振荡传递路径。
阻尼路径3 具体可描述为:当ΔPe发生变化时,扰动由ΔUdc传递至Δil,由Δil传递至Δur,再由Δur传递至ΔPe的通路。阻尼路径3 经过光伏电站、LCCHVDC 系统、交流系统3 个子系统,且路径3 内部包含2 条闭合回路a、b:闭合回路a 经过Δil、Δur,由传递函数矩阵ZPV(s)、YPV2(s)构成,体现了光伏与交流系统的次同步交互作用;闭合回路b 经过Δir、Δur,由传递函数矩阵ZLCC(s)、YLCC(s)构成,体现了交流系统与LCC-HVDC 系统的次同步交互作用。闭合回路a、b 在公共耦合点Δur处交互作用,组成闭合交叉环路。当Δur遭受扰动时,由于闭合回路a、b 的存在,Δil、Δir产生变化,并再一次影响到Δur的动态,进而导致光伏与LCC-HVDC 系统间形成闭环扰动路径。故称阻尼路径3 为光伏与LCC-HVDC 系统的振荡耦合路径。
结合阻尼路径,将次同步交互作用过程分为光伏内部各控制器间的交互作用及光伏与LCCHVDC 系统、交流系统间的交互作用两类:光伏内部各控制器间的交互作用可以解释为,在光伏电站内部,扰动经闭合回路(阻尼路径1、2)使光伏内部控制器间产生交互影响的动态过程;光伏与LCCHVDC 系统、交流系统间的交互作用可以解释为公共耦合点电压、电流扰动经闭合交叉环路(阻尼路径3)相互驱动导致各子系统间交互影响,形成光伏与交流系统间的交互作用(后称“光伏-交流系统交互作用”)、光伏经交流系统与LCC-HVDC 系统的交互作用(后称“光伏-LCC-HVDC 交互作用”)。故PVSL 系统的次同步交互作用机理可以概述为:由于光伏自身的闭合回路、光伏与LCC-HVDC 系统、交流系统间的耦合路径均经过与直流电容振荡模态相关的传递函数,故光伏自身、光伏-LCC-HVDC 交互作用、光伏-交流系统交互作用均会对直流电容振荡模态产生影响。
因此,在工程实际中,可以依据次同步交互作用机理及阻尼特性分析结果,优选控制器参数,设计阻尼控制器,二者配合实现SSO 的综合抑制。
4 光伏与LCC-HVDC 系统次同步交互作用的阻尼特性分析
鉴于直流电容振荡模态与机电振荡模态动态方程的相似性,本章将同步发电机的阻尼转矩法应用于直流电容主导的振荡模态。在此基础上,提出一种阻尼分离方法,提取各类次同步交互作用对SSO阻尼的影响。最后,结合算例进行仿真分析,对该方法的有效性进行验证。
4.1 基于直流电容振荡模态的阻尼转矩法
由于光伏的直流电容动态方程与同步发电机的转子动态方程具有相似的形式[31],本节将用于分析同步发电机低频振荡问题的阻尼转矩法[32],推广至本文的SSO 模态分析中,现对其推广过程进行阐述。
由附录B 式(B3)可得直流电容环节输入功率、输出功率和直流电容电压的关系为:
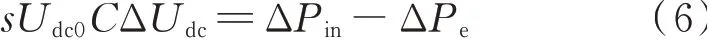
式中:Udc0为直流电容电压稳态值。
由第3 章可知,若在ΔUdc处将传递路径断开,可以分别得到由ΔUdc至ΔPin和ΔUdc至ΔPe的开环传递函数Gx(s),因此式(6)等式右侧可以表示为:
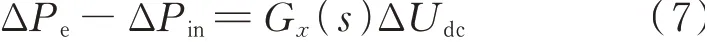
令G(s)=sGx(s),Δxdc=ΔUdc/s,求解出由Δxdc至ΔPe-ΔPin、用以表征除直流电容环节外系统其他环节的传递函数G(s),包括光伏电站、交流系统和LCC-HVDC 子系统的动态特性。由此,式(7)变换至如下形式:
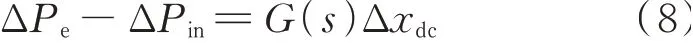
对于弱阻尼振荡模式,近似有s=jω。将式(8)代入式(6)并代入s=jω,将G(s)展开,使其表示为实部、虚部相加的形式,并通过傅里叶变换将方程转换至时域中,则式(6)可转换为:
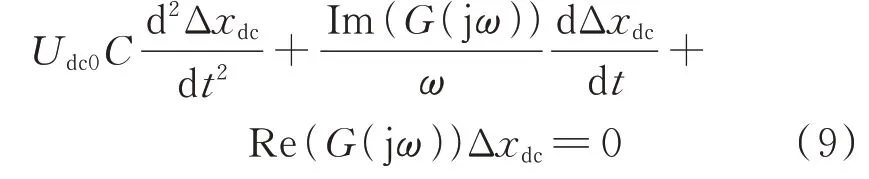
参考阻尼转矩法中二阶运动方程的相关概念,定义电气惯量Ka=Udc0C,阻尼系数Kb=Im(G(jω))/ω,同步系数Kc=Re(G(jω))。根据阻尼转矩法稳定性判据[32],对PVSL 系统直流电容振荡模态的稳定性进行判断:Kb>0 时,PVSL 系统振荡模态稳定;Kb<0 时,PVSL 系统振荡模态失稳,且Kb越小,所提供的负阻尼越大,越不利于系统的稳定。因此,Kb可以作为系统发生SSO 时阻尼大小的量化指标。
4.2 阻尼分离方法
由图3 可知,阻尼路径1、2 均属于光伏自身的交互作用,阻尼路径3 同时包含了光伏与交流系统、光伏与LCC-HVDC 系统的次同步交互作用。本节提出一种阻尼分离方法,根据线性系统叠加原理,依照响应分量的分类,合并阻尼路径1、2,对框图中阻尼路径3 中的闭环交叉点Δur进行解耦,重新构建框图,量化次同步交互作用提供的阻尼,提取这2 种次同步交互作用对PVSL 系统的影响,阻尼分离步骤如图4 所示。
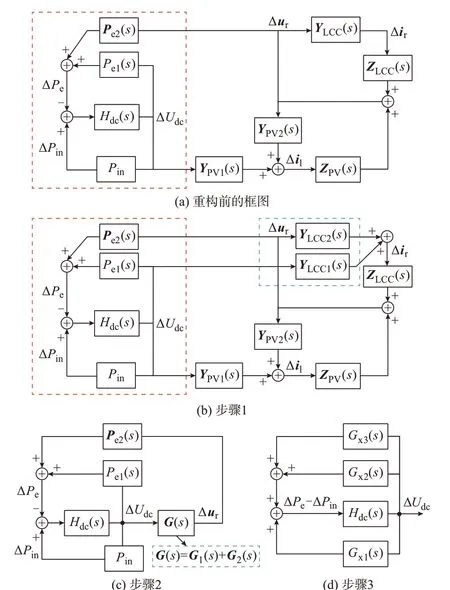
图4 阻尼分离步骤Fig.4 Damping separation step
步骤1:图4(a)为重构前的框图,重构目标是将红色虚线框之外的传递函数转化为对应于光伏自身、光伏与交流系统间、光伏与LCC-HVDC 系统间次同步交互作用的3 种传递函数。为便于框图重构,将外部系统以ΔUdc至Δur的传递函数形式表示,应先对LCC-HVDC 系统的输入量进行适当选择,引入变量ΔUdc作为LCC-HVDC 系统传递函数的输入量,由变量Δur、ΔUdc表示输出量Δir,将式(3)和式(5)代入式(4)中,可以求解出新的开环传递函数关系,如式(10)所示;其对应框图如图4(b)所示,重构部分已在图中用蓝色虚线框标出。
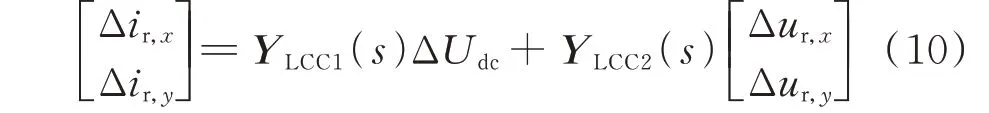
式中:
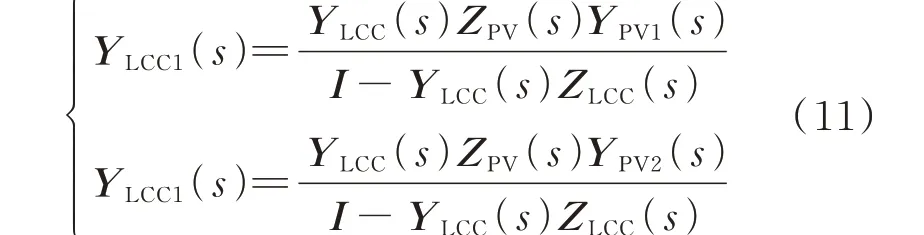
步骤2:在图4(b)的基础上对红色虚线框之外的框图进行化简,将式(3)和式(10)代入式(5)中,替换中间变量Δil、Δir,可以得到由ΔUdc至Δur的开环传递函数矩阵G(s),G(s)包含了光伏与交流系统之间、光伏与LCC-HVDC 系统之间的两种次同步交互作用;令Δir=0,即认为LCC-HVDC 系统不接入系统,不考虑光伏-LCC-HVDC 交互作用时,对红色虚线框之外的框图进行化简,将式(3)代入式(5)中,可以得到对应开环传递函数矩阵G1(s),G1(s)表示光伏-交流系统交互作用;根据线性系统叠加原理,将G(s)与G1(s)相 减 得 到G2(s),G2(s)表 示 光 伏-LCC-HVDC 交互作用。G(s)、G1(s)、G2(s)的具体表达式如式(12)所示,其中I为单位矩阵,对应框图如图4(c)所示。
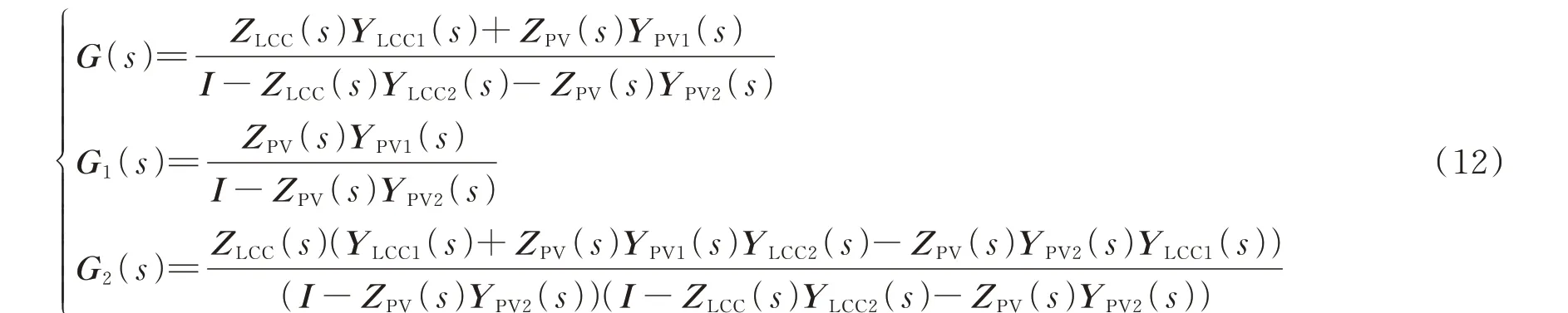
步 骤3:化 简 图4(c)所 示 框 图,保 留ΔUdc和ΔPe、ΔPin作为输入、输出变量,得到阻尼分离后由变量ΔUdc分别至变量ΔPe-ΔPin、ΔPe的3 项传递函数,如式(13)所示,其对应框图如图4(d)所示。
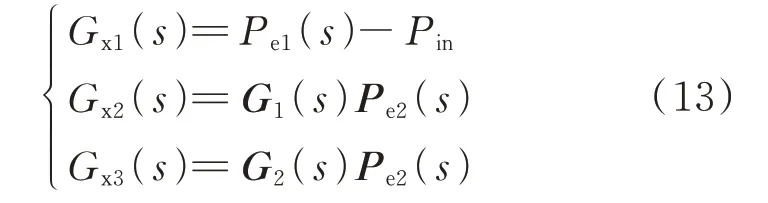
在式(13)中,Gx1(s)表征光伏内部阻尼,Gx2(s)表征光伏-交流系统交互作用对PVSL 系统的SSO阻 尼,Gx3(s)表 征 光 伏-LCC-HVDC 交 互 作 用 对PVSL 系统的SSO 阻尼。根据式(7)至式(9),定义Gx1(s)对 应 的 阻 尼 系 数Kb1为 光 伏 阻 尼 系 数,定 义Gx2(s)对应的阻尼系数Kb2为光伏-交流系统交互作用的阻尼系数,Gx3(s)对应的阻尼系数Kb3为光伏-LCC-HVDC 交互作用的阻尼系数。由叠加原理可知,系统总响应分量等于各类次同步交互作用的响应分量之和,故三者之和Kb为PVSL 系统总阻尼系数。通过阻尼分离法计算阻尼系数,能够定量地评估各类次同步交互作用对PVSL 系统的影响。对于任意动态方程可以变换为二阶运动方程的振荡元件,均能够采用本文所用方法进行对应SSO 模态的阻尼特性分析。
4.3 PVSL 系统的阻尼特性分析
本节基于图1、附录A 表A1 至表A3 对应的算例,采用阻尼分离法分析PVSL 系统各类次同步交互作用对SSO 模态的影响,并结合时域仿真分析验证该方法的有效性。本文所用方法的稳定性判据及稳定状态下PVSL 系统的阻尼特性分析详见附录C和D,现对振荡状态下的PVSL 系统进行阻尼特性分析。打开图1 中的开关K,模拟电网强度变弱引发SSO 的情况,采用阻尼分离法求得PVSL 系统的阻尼系数-频率特性曲线(后称“特性曲线”)如图5所示,其中Kb1为光伏阻尼特性曲线,Kb2为光伏-交流系统交互作用的阻尼特性曲线,Kb3为光伏-LCCHVDC 交互作用的阻尼特性曲线,Kb为PVSL 系统阻尼特性曲线。
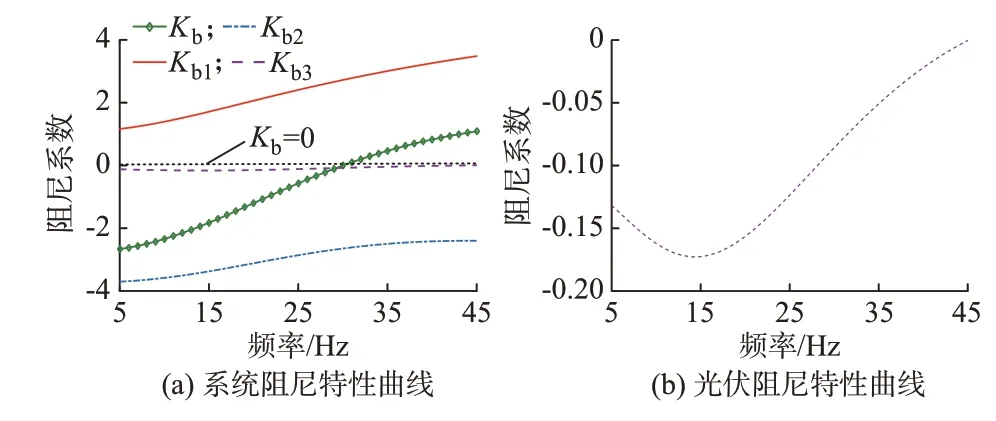
图5 阻尼系数-频率特性曲线Fig.5 Damping coefficient-frequency characteristic curves
由图5 可知,Kb1始终为正值,光伏自身为PVSL系统提供正阻尼,光伏并入无穷大系统时不存在发生SSO 的风险;Kb2、Kb3在次同步频域内均为负值,光伏-交流系统交互作用、光伏-LCC-HVDC 交互作用为PVSL 系统提供负阻尼,使系统更容易发生SSO;此外,Kb3对应特性曲线在5~25 Hz 频率范围内阻尼系数最小,在该频段内光伏-LCC-HVDC 交互作用最为强烈;叠加Kb1、Kb2、Kb3得到Kb,其对应特性曲线在5~30 Hz 频率范围内为负值,PVSL 系统存在SSO 失稳的风险。综上,光伏-交流系统交互作用与光伏-LCC-HVDC 交互作用均为PVSL 系统提供负阻尼,考虑这2 种次同步交互作用时,PVSL 系统SSO 模态阻尼减小,SSO 更加剧烈。
为验证上述阻尼特性分析所得讨论结论的正确性与阻尼分离法的有效性,在PSCAD/EMTDC 中搭建算例对应的时域仿真模型,对比该场景与光伏并入无穷大系统、光伏并入弱交流系统(短路比为2.4)3 种场景下振荡幅度的大小。后两种场景不考虑LCC-HVDC 系统的动态特性,为排除系统潮流变化对稳定性造成的影响,在对应模型中采用恒流源代替LCC-HVDC 系统。分别对上述3 种场景下的模型进行时域仿真,4.0 s 时打开开关K,3 种场景下Udc的时域仿真波形如图6 所示。

图6 3 种场景下的直流电容电压Fig.6 DC capacitor voltage in three scenarios
由图6 可知,光伏并入无穷大系统时Udc没有发生SSO,与上述讨论中Kb1始终为正值的结论相符;而PVSL 系统4.0 s 后Udc出现了SSO,与上述讨论中Kb在5~30 Hz 频率范围内为负值的结论相符;对比光伏并入弱交流系统与并入无穷大系统的时域仿真结果可知,并入弱交流系统后Udc出现SSO,表明光伏-交流系统交互作用为系统提供负阻尼,与上述讨论中Kb2在次同步频域内为负值的结论相符;对比PVSL 系统与并入弱交流系统的时域仿真结果可知,接入LCC-HVDC 系统后Udc的SSO 幅度更大,表明光伏-LCC-HVDC 交互作用削弱PVSL 系统阻尼,与上述讨论中Kb3在次同步频域内为负值的结论相符。由时域仿真验证可知,在本文所用的PVSL算例中,光伏与交流系统、光伏与LCC-HVDC 系统的次同步交互作用为直流电容模态提供负阻尼,同时验证了阻尼分离法的有效性。需要注意的是,该结论是基于算例进行阻尼特性分析所获得的讨论结论,在不同设备、不同参数条件下,两类次同步交互作用对SSO 的影响有可能改变。
5 影响因素分析
由第3 章分析过程可知,PVSL 系统SSO 模态与光伏逆变器外环控制参数、光伏自身运行工况、LCC-HVDC 系统控制器参数相关。本章据此选取影响因素,分析其对算例SSO 模态阻尼特性的影响;同样地,所得结论为定性结论,与PVSL 系统的结构和参数有关。此外,本文还对交流系统强度变化对SSO 的影响进行了分析,由于现有文献对此已有一致的结论[8-9,23],故将其放至附录E。
5.1 光伏逆变器参数
1)光伏逆变器外环比例系数Kppv
对算例的影响因素进行阻尼特性分析,打开图1 中的开关K,算例参数与附录A 表A1 至表A3 中参数相同,其他影响因素分析的工况设置与此处一致。 当Kppv分 别 为0.5Kppv0、1.0Kppv0、2.0Kppv0时,PVSL 系统的特性曲线如附录F 图F1 所示。由图F1 可知,随着Kppv的增大,Kb1上移,光伏所提供的阻尼增强;Kb2、Kb3下移,光伏-交流系统交互作用、光伏-LCC-HVDC 交互作用为PVSL 系统提供的阻尼减弱。Kb1、Kb2、Kb3叠加得到Kb,随着Kppv的增大,Kb上移,系统直流电容振荡模态阻尼增强。
基于PSCAD/EMTDC 平台对上述讨论结论进行时域仿真验证,算例仿真工况如下:4.0 s 时,打开图1 开关K,在线路中串联电感L0以引发SSO,其他影响因素分析的工况设置与此处一致。当Kppv分别为0.5Kppv0、1.0Kppv0、2.0Kppv0时Udc的时域仿真曲线如附录F 图F2 所示。由图F2 可知,随着Kppv的增大,Udc的振荡幅度减小,与上述结论一致。
2)光伏逆变器外环积分系数Kipv
当Kipv分 别 为15、25、35 时,PVSL 系 统 的 特 性曲线如附录F 图F3 所示。由图F3 可知,随着Kipv的增 大,Kb1下 移,光 伏 所 提 供 的 阻 尼 减 弱;Kb2、Kb3下移,光伏-交流系统交互作用、光伏-LCC-HVDC 交互作用为PVSL 系统提供的阻尼减弱。Kb1、Kb2、Kb3叠加得到Kb,随着Kipv的增大,Kb下移,系统直流电容振荡模态阻尼减弱。
基于PSCAD/EMTDC 平台对上述讨论结论进行时域仿真验证,当Kipv分别为15、25、35 时,Udc的时域仿真曲线如附录F 图F4 所示。由图F4 可知,随着Kipv的增大,Udc的振荡幅度增加,与上述结论一致。
5.2 光伏自身运行工况
当光伏光照强度S分别为700、850、1 000 W/m2时,PVSL 系统的特性曲线如附录F 图F5 所示。由图F5 可知,随着S的增大,Kb1轻微上移,光伏所提供的阻尼稍有增强;Kb2、Kb3下移,光伏-交流系统交互作用、光伏-LCC-HVDC 交互作用为PVSL 系统提供的阻尼减弱。Kb1、Kb2、Kb3叠加得到Kb,随着S的增大,Kb下移,系统直流电容振荡模态阻尼减弱。
基于PSCAD/EMTDC 平台对上述讨论结论进行时域仿真验证,当S为700、850、1 000 W/m2时Udc的时域仿真曲线如附录F 图F6 所示。由图F6 可知,随着S的增大,Udc的振荡幅度增大,与上述结论一致。
5.3 LCC-HVDC 系统控制器参数
1)LCC-HVDC 系统控制器比例系数Kpdc
当Kpdc分 别 为0.5Kpdc0、1.0Kpdc0、2.0Kpdc0时,PVSL 系统的特性曲线如附录F 图F7 所示。由图F7 可知,随着Kpdc的增大,Kb1、Kb2不变;Kb3上移,光伏-LCC-HVDC 交互作用为PVSL 系统提供的阻尼增强。Kb1、Kb2、Kb3叠加得到Kb,随着Kpdc的增大,Kb上移,系统直流电容振荡模态阻尼增强。
基于PSCAD/EMTDC 平台对上述讨论结论进行 时 域 仿 真 验 证,当Kpdc分 别 为0.5Kpdc0、1.0Kpdc0、2.0Kpdc0时,Udc的时域仿真曲线如附录F 图F8 所示。由图F8 可知,随着Kpdc的增大,Udc的振荡幅度减小,与上述结论一致。
2)LCC-HVDC 系统控制器积分系数Kidc
当Kidc分别为0.5Kidc0、1.0Kidc0、2.0Kidc0时,PVSL系统的特性曲线如附录F 图F9 所示。由图F9 可知,随 着Kidc的 增 大,Kb1、Kb2不 变;Kb3下 移,光 伏-LCC-HVDC 交互作用为PVSL 系统提供的阻尼减弱。Kb1、Kb2、Kb3叠加得到Kb,随着Kidc的增大,Kb下移,系统直流电容振荡模态阻尼减弱。
基于PSCAD/EMTDC 平台对上述讨论结论进行 时 域 仿 真 验 证,当Kidc分 别 为0.5Kidc0、1.0Kidc0、2.0Kidc0时,Udc的 时 域 仿 真 曲 线 如 附 录F 图F10 所示。由图F10 可知,随着Kidc的增大,Udc的振荡幅度增大,与上述结论一致。
6 结语
本文搭建了PVSL 系统的闭环传递函数模型,采用阻尼分离法对系统的SSO 阻尼路径及其阻尼特性展开研究,并通过时域仿真进行验证,得到的结论如下。
1)基于线性化运动方程,建立了保留直流电容及控制器动态环节的系统框图,清晰展现各子系统间交互作用关系及振荡耦合路径,有利于PVSL 系统次同步交互作用的分析。
2)通过对框图的聚合处理,构造出PVSL 系统直流电容模态的3 条阻尼路径:光伏输入功率振荡传递路径、光伏电磁功率振荡传递路径、光伏与LCC-HVDC 系统的振荡耦合路径。结合阻尼路径,将次同步交互作用归纳为光伏内部各控制器间的交互作用及光伏与LCC-HVDC 系统、交流系统间的交互作用两类。
3)提出一种阻尼分离方法,能够有效评估系统内次同步交互作用提供的阻尼。在本文算例中,光伏与弱交流系统间、光伏与LCC-HVDC 系统间的次同步交互作用会削弱直流电容模态的阻尼,故考虑这两种次同步交互作用时,系统SSO 现象更加剧烈。
4)分析参数变化对算例SSO 稳定性的影响:增大LCC-HVDC 系统定电流控制器和光伏逆变器外环比例系数、减小LCC-HVDC 系统定电流控制器和光伏逆变器外环积分系数及光伏光照强度,能够增强系统SSO 阻尼。
本文仅针对直流电容振荡模态展开阻尼路径及特性分析,后续可综合考虑PVSL 系统中的多种振荡模态,开展相关的SSO 问题研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
