飞机起落架双腔式油气缓冲器非线性动力学特性研究

祝世兴，李佩窈，祝恒佳，魏戬

(1.中国民航大学航空工程学院，天津 300300；2.昆明理工大学机电工程学院，云南昆明 650000)

0 前言

缓冲器是所有现代飞机不可或缺的部分，目前油气缓冲器在现代飞机上应用最为广泛[1-2]。双腔式油气缓冲器包含低压腔和高压腔2个空气腔，拥有单腔缓冲器优点的同时在应对粗糙路况时的吸能特性也得到明显改善。双腔式油气缓冲器刚度特性对改善飞机在冲击振动、高速滑跑时的运行品质，提升乘客的舒适度，保护飞机零部件以及仪表设备等方面影响较大。目前，缓冲器的刚度特性一般采用激振试验的方法获得，但是由于试验自身的滞后性、周期长以及成本高等缺点，采用仿真模拟的方法精确地模拟其动态特性成为研究趋势[3-5]。双腔式油气缓冲器内部结构复杂，一般的仿真模拟并没有考虑到流体在工作过程中的流动损失对缓冲器整体刚度特性的影响。因此，为更接近缓冲器实际工作情况，采用流固耦合仿真方法对双腔式油气缓冲器整体的刚度特性进行研究是非常重要的。

早期的双腔式缓冲器多应用于直升机上，并且大部分是对起落架整体进行研究，而针对双腔式缓冲器的单独研究较少。文献[6]中研究了符合直升机地面共振稳定性要求的起落架刚度及阻尼的优化设计方法。文献[7]中利用动力学分析软件ADAMS对起落架进行了落震动力响应的模拟与分析。文献[8]中对大柔性飞机起落架缓冲器参数进行了优化设计。文献[9]中利用ADAMS建立了柔性活塞杆的缓冲器动力学模型并进行了落震仿真模拟，探讨活塞杆刚度对缓冲器吸能特性的影响。大多数研究中均将起落架简化为二自由度弹簧质量块模型，将缓冲器简化为所需力的形式加载到质量块上，但这并未考虑到起落架结构的弹性特性和缓冲器的空气弹簧和阻尼的非线性特性。因此，文献[10]中利用哈密顿变分原理，建立了弹性结构的起落架动力学模型，以弥补上述缺点。对于直升机起落架的防“地面共振”设计和抗坠毁能力，文献[11]中设计了一种单级双腔缓冲器，其中高压腔与低压腔分离，并且保留了单级双腔缓冲器的优点，串联双腔缓冲器目的是将飞机的起飞着陆和耐坠毁缓冲行程进行分离。文献[12]中利用等效线性化方法，分析了串联双腔缓冲器在多种频率下的缓冲器等效刚度和当量阻尼分析值。文献[13]中利用流固耦合及动网格方法，对缓冲器的阻尼特性进行了仿真。但是到目前为止，仍缺少考虑缓冲器复杂的流固耦合问题尤其是缓冲器工作过程中流体的流动损失有限元模拟问题对缓冲器刚度特性影响的相关算例与研究。

本文作者以某大型民航客机主起落架为例，建立适用于ABAQUS的双腔油气缓冲器仿真模型。利用工程估算方法模拟缓冲器冲击过程并与ABAQUS中的仿真结果进行比对，验证ABAQUS中模型的可用性；采用正弦激励，分析缓冲器随幅值和频率变化时的刚度特性；采用随机激励，模拟实际工况，分析缓冲器的动态特性，从而为双腔式缓冲器结构性能的优化提供依据，并为进一步利用ABAQUS软件开发缓冲器样机设计奠定基础。

1 双腔缓冲器模型描述

如图1所示，双腔式缓冲器低压腔与高压腔通常充入一定初始气压的干燥氮气或空气，工作时活塞运动使油腔中的油液流向低压腔压缩气体，同时吸收能量。油液在外力的作用下，流经油孔耗散掉起落架一部分能量。当低压腔的空气压力与油液阻尼力增加到等于高压腔初始压力时，位于高低压腔之间的活塞开始移动，高压腔开始被压缩[14]。压缩缓冲器使得活塞上移称为“正行程”。经过初始冲击后，空气腔气体作为弹性体开始膨胀释放能量，迫使油液又反流回油腔，活塞向下移动，此过程称为“反行程”。经过一正一反2个行程完成一个循环，经多个循环，可耗散掉绝大部分飞机降落时产生的能量，进一步达到减震的效果。飞机的着陆撞击时间在0.6～0.9 s之间[15]。正反行程总时间不超过0.8 s。

图1 缓冲器结构

2 缓冲器数学建模

缓冲器轴向力Fs是由空气弹簧力Fa、油液阻尼力Fh、缓冲器结构限制力Fl以及内部摩擦力Ff构成[16]。

Fs=Fa+Fh+Fl+Ff

(1)

结合气体多变方程式可以得到空气弹簧力的力学方程为

(2)

利用MATLAB拟合缓冲行程和活塞行程为

s=8.582×104t5-1.064×105t4+4.769×

104t3-1.025×104t2+1 180t

(3)

s′=1.276×104t4-1.203×104t3+3 180t2-124t

(4)

油液阻尼力是油液流过油孔时，油孔两侧存在压力差而产生的[17]。假设油液为不可压缩流体，由Bernoulli方程和连续性方程[18]可以得到油液阻尼力为

(5)

其中：Ah是缓冲器有效压油面积；Aoil是油孔截面积；Cd是油孔缩流系数；ρ是油液密度。

缓冲器内部库仑摩擦力假定为一个由缓冲器弯曲位移引起的内部摩擦力和内部压力引起的内部摩擦力的合力，表达式为

Ff=Ff1+Ff2

(6)

缓冲器弯曲位移引起的内部摩擦力为

(7)

其中：μb是库仑摩擦因数；Nu和NL分别是活塞对缸体的作用力与柱塞对缸体的作用力。

缓冲器内部压力引起的内部摩擦力为

(8)

其中：Db是轴套直径；Hb是轴套高度。

缓冲器的设计要求指出:缓冲器系统应适当保留某些行程余量，吸收给定过载下的使用功量[1]。只有在极端条件下，才允许缓冲系统吸收最大的功量。正常使用情况下,缓冲器结构限制力为0，只有在过度伸长与极限压缩的情况下才考虑结构限制力。文中仿真缓冲器正常的使用情况，所以结构限制力为0。

缓冲器的模型参数如表1所示。

表1 缓冲器模型参数

3 有限元模型建立

缓冲器在工作过程中，大致分为两类接触问题：第一类是缸体与活塞和柱塞的摩擦接触，ABAQUS中对于此类接触问题常采用拉格朗日法进行计算；第二类是氮气和油液与缸体、活塞和柱塞的接触，应采用流固耦合的方法进行计算。对于流固耦合问题，ABAQUS中通常采用欧拉-拉格朗日(CEL)接触算法来模拟流体与固体边界处高速的相互作用。CEL方法中固体采用拉格朗日单元、流体采用欧拉单元，欧拉单元可以克服流体大变形下网格严重扭曲的现象，并且与拉格朗日单元不同之处在于:拉格朗日单元随材料移动而移动，欧拉单元是材料在单元内流动。如图2所示。

图2 连续体变形

在默认情况下，欧拉体内部是没有任何材料的，因此采用CEL方法的关键在于材料的填充，应在Load模块下对相应的欧拉体区域进行操作。该模型材料的属性定义如表2所示，其中Eos: US-UP为Mie-Grüneisen状态方程中定义流体的材料参数。

表2 油气材料属性定义

在通常情况下，建立油气缓冲器有限元模型时需要考虑氮气腔、油腔、柱塞、活塞、缸体等，为提升计算速度，应将模型进行必要的简化。假定油液密封性良好，将密封圈简化为柱塞的一部分，不予以考虑,去除不必要的转角与沟槽,忽略缓冲器自身重力的影响等。

该模型中，缓冲器柱塞与缸体采用C3D8R六面体单元，气体与液体采用EC3D8R单元，进行材料的填充。利用ABAQUS/CAE建立缓冲器三维实体模型，而后建立离散单元模型，离散刚体单元有41 339个，其中C3D8R有26 438个、EC3D8R有14 901个，如图3所示。

图3 网格划分

应用ABAQUS/Explicit模块进行动态分析，缓冲器有限元模型计算过程分为2个部分：(1)在特定的频率与幅值下给予上端一个冲击位移，模拟缓冲器的冲击过程，输出随时间变化的缓冲器轴向力曲线；(2)给予缓冲器不同的动态激励，模拟它的运动状态与工作特性。

4 模型仿真与结果分析

有限元模型建立后，利用软件按照设定的要求进行仿真分析，直到设定的仿真时间为止。缓冲器的正反行程总时间不超过0.8 s，模型设定的仿真时间到0.5 s为止。

4.1 冲击过程

给予缓冲器上端240 mm的垂向位移，模拟缓冲器冲击过程。图4和图5分别为压缩过程中缓冲器的内部流速与内部液体压力。

图4 缓冲器的内部流速

图5 缓冲器内部液体压力

基于理论基础建立数学模型，采用MATLAB软件编写相应的计算程序，得到空气弹簧力、油液阻尼力、缓冲器轴向力随时间变化的曲线，并将ABAQUS仿真结果与MATLAB结果进行比对，分析二者之间的误差。

缓冲器正行程时间约为0.23 s，图6所示是空气弹簧力的理论值与仿真值随时间变化曲线。可知：在t=0.13 s之前只有低压腔被压缩，t=0.13 s后高压腔处于压缩阶段;在t=0.19 s后，由于空气腔的气体在高压状态下液化导致气体温度升高，内能增加并伴随了一定的动能损失，所以在t=0.19 s之后理论值与仿真值产生了较大误差。

图6 空气弹簧力随时间变化曲线 图7 油液阻尼力随时间变化曲线

图7所示为油液阻尼力理论值与仿真值随时间变化曲线。可知：油液阻尼力随时间的增加先增加后减小，这是因为缓冲器内部回油孔前后压差处于先增加后减小的趋势，使得油液流速处于先增加后减慢的情况。

数值仿真和有限元仿真的误差可以通过均方根值来定义：

(9)

式中：m表示离散力信号的数据个数；FNUM和FSIM分别表示数值仿真和有限元仿真的输出力。

表3所示为空气弹簧力和油液阻尼力的数值仿真和有限元仿真之间的误差大小，可以看出：空气弹簧力的误差较大，但由于空气弹簧力的平均值为17 609 N，因此误差是可以接受的，验证了文中建立的缓冲器有限元模型的可用性。

表3 不同仿真模型之间的误差 单位：N

图8所示为缓冲器轴向力理论值与仿真值随时间变化的曲线，可得：理论值与仿真值相对误差为0.96%，从而验证了仿真模型的准确性。

图8 缓冲器轴向力随时间变化曲线

经比对，空气弹簧力、油液阻尼力和轴向力仿真值与理论值误差均小于1%，证明了该模型的可用性，为后续研究缓冲器特性提供了参考。

4.2 不同激振对缓冲器等效动刚度影响

在缓冲系统运行过程中，外界环境温度与充气压力的改变会直接影响缓冲系统的性能。初始扰动的大小会影响起落架的振动幅值，飞机装载不同会引起机体转动惯量的变化，从而导致起落架固有频率的改变[19]。因此，本文作者给予缓冲器不同位移激励方式，改变频率与幅值，观察其变化情况。

图9所示为冲击激励下缓冲器内部流体压力，显示了缓冲器在工作过程中油液流动时的喷溅现象。由于空气压缩的速度很快，以至于在压缩过程中空气所产生的热量来不及向外界传递，因此空气压缩的过程可近似看成绝热过程。但油液高速流动时会发生喷溅现象，与低压腔的气体进行强烈的热交换，因此空气压缩的过程为多变过程。图9也从侧面说明了在压缩过程中低压腔的多变过程。

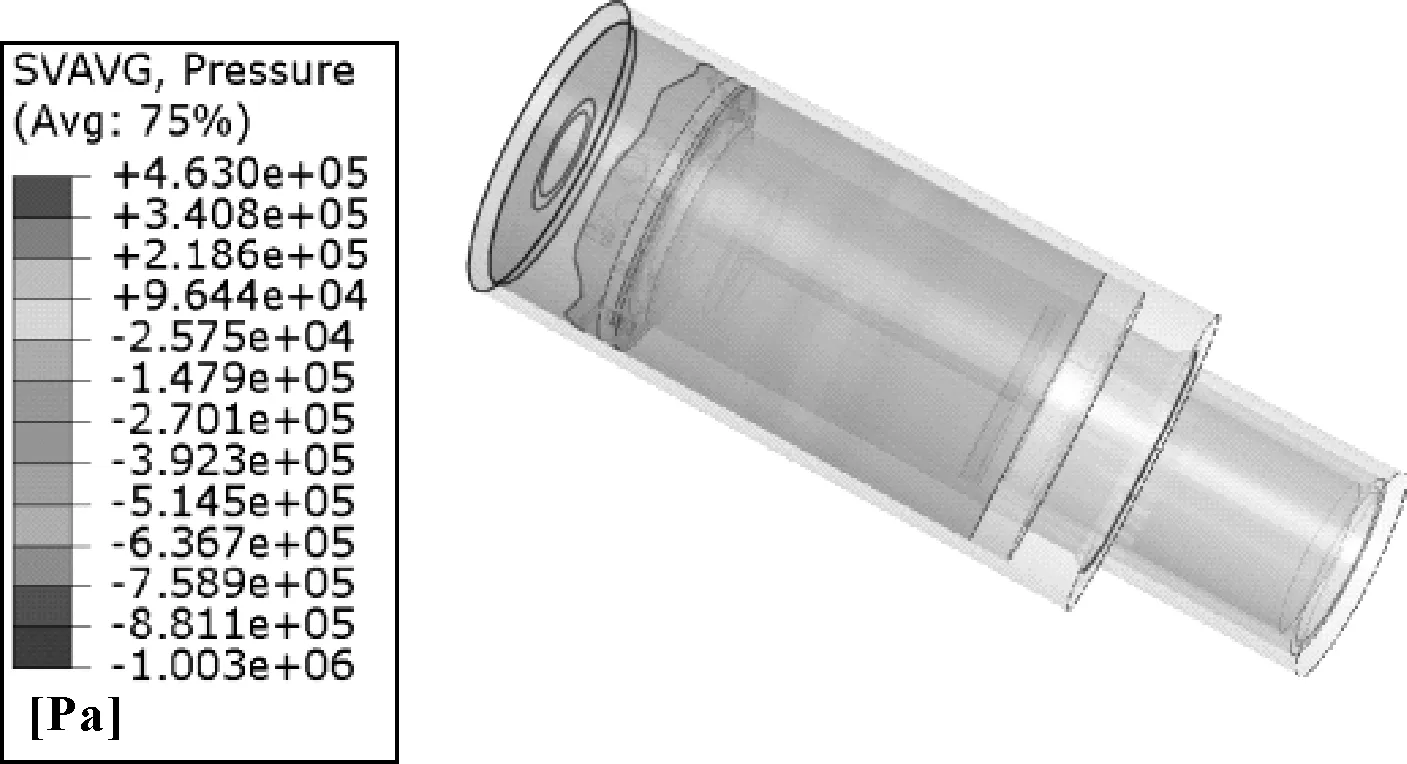
图9 冲击激励下缓冲器内部流体压力

设对缓冲器施加的位移激励为简谐激励，表达式为

x(t)=H0+Hsinωt

(10)

其中：ω为激振力的圆频率，ω=2πf；f为激励频率；H为激励幅值；H0为初始压缩量。

根据双腔式磁流变减振器的轴向力与位移功量图，结合式(11)求得缓冲器的等效动刚度K为

(11)

假定缓冲器的振动幅值保持12 mm不变，缓冲器等效动刚度随振动频率的变化如图10所示。可以看到：随频率的增加等效动刚度降低，当频率超过8 Hz时，等效动刚度降低速度减慢。

图10 频率对等效动刚度的影响

假定缓冲器的振动频率保持2 Hz不变，以不同振幅的正弦位移信号作为输入，图11所示为缓冲器在激振幅值为6 mm时的力-位移迟滞曲线，其中位移为正时表示压缩，为正行程；位移为负时表示拉伸，为负行程。图12所示为幅值对等效动刚度的影响,可以看出：幅值与等效动刚度呈现严重的非线性特性，随振动幅值增加等效动刚度减小；与频率对等效动刚度的影响相比，幅值的变化对等效动刚度的影响较大。

图11 激振幅值为6 mm时的力-位移曲线 图12 幅值对等效动刚度的影响

然而，正弦激励在实际工作过程中很少遇到，作为隔振元件的油气缓冲器被广泛应用于随机振动的环境中。随机信号可以通过离散傅里叶变换分解为一系列具有不同频率和幅值的简谐波。谐波叠加法基本原理是将路面的不平度表示为大量具有随机相位的正弦或余弦谐波之和[20]。

在ABAQUS中，可以考虑采用周期形幅值曲线来近似代替随机激励，以产生伪随机激励曲线。周期形幅值曲线用傅里叶级数表示，表达式为

(12)

式中：N为傅里叶级数项的个数；t0为起始时刻；A0为初始幅值；An为cos项的系数；Bn为sin项的系数。

取A0=0.01、t0=0，频率与幅值按照表4取值。

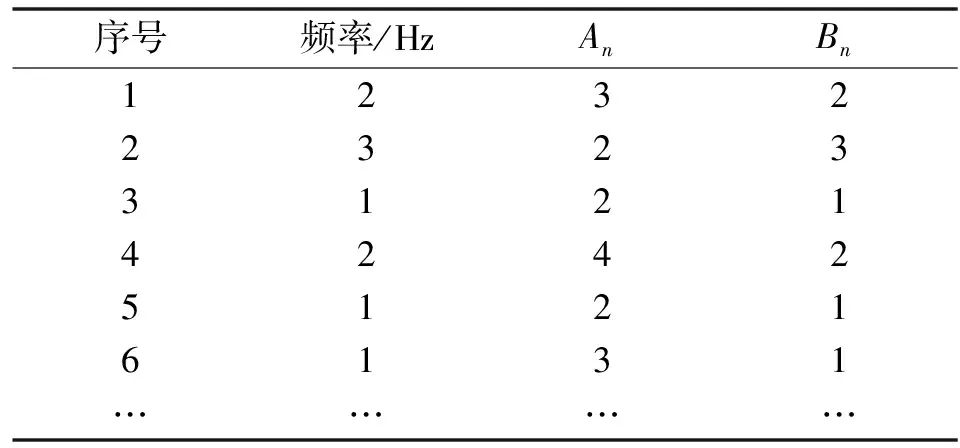
表4 伪随机激励曲线幅值与频率部分取值

图13所示为伪随机位移激励时域曲线，图14所示为0.2～1 s缓冲器输出的轴向力。选取此时间段是整个仿真过程中的随机选择，以方便观察轴向力变化趋势。由图14可以看出：有限元方法输出缓冲器轴向力略小于数值方法输出的缓冲器轴向力，原因是油液与筒壁之间产生摩擦从而引起沿程损失，但总体趋势一致。

图13 伪随机位移激励时域曲线 图14 0.2～1 s内的轴向力

5 结论

通过建立起落架双腔缓冲器的数学模型与有限元模型，模拟不同工况下的缓冲器工作特性，得到以下结论：

(1)与数学模型相比，基于流固耦合有限元模型可以较好地处理油液在流动过程中产生的压力损失，与缓冲器的实际工况更为接近；有限元仿真分析结果与数学模型计算结果在大位移冲击作用下相对误差均小于1%，进一步说明了有限元模型的可行性；

(2)在正弦激励工况下，随激振频率与幅值的改变，缓冲器等效动刚度表现出分段非线性动力学特性，随频率与幅值的增加等效动刚度减小，并且幅值的改变对等效动刚度产生的影响较大；

(3)在随机激励工况下，由于油液的流动损失导致了仿真结果小于理论结果，但仿真结果的总体趋势与理论结果基本保持一致，吻合度较高。