川渝裂缝性地层自动压井环空多相压力波速特性研究*

孔祥伟， 刘祚才， 靳彦欣

（1. 长江大学 石油工程学院，武汉 430000；2. 长江大学 油气钻完井技术国家工程研究中心，武汉 430000；3. 中石化西南石油工程公司重庆钻井分公司，重庆 400000；4. 中国石油化工股份有限公司青岛安全工程研究院，山东 青岛 266000）

引 言

川渝地区地质情况复杂，面临异常高压、多压力系统、裂缝溶洞性地层，井底易出现裂缝气、压差气等复杂气流，以及循环排气后效时间长等施工难点，需频繁循环排气和压井作业[1-3].目前，国外的哈里伯顿公司已实现了实时自动压井系统，并已投入使用；国内的研究机构研发了多种压井模拟系统，多采用低泵冲立压法控制井筒压力，控压精度不高，不能适应裂缝气地层窄密度窗口实时压井的需要.国内压井作业还没有实现自动化压井，也无自动压井系统，无法根据实时录井参数自动控制回压，实时自动压井系统的难点是目标回压值与节流阀调节时间间隔确定[4-6].准确计算环空压力波传播速度，可得到压力波沿环空的传播周期，为节流阀开度调控间隔时间提供理论基础[7-8].

石油管道压力波速的研究始于19 世纪，随后，国外学者推导了关于均质流、分层流的波速基本公式[9-10].到21 世纪，波速的研究更细致化，压力波速应用至柴油、蒸汽、纳米铝热剂反应、交叉管道、气动管道、环道实验、输油管道、黏弹性管道、瞬态混相流、动力压力波、高低纬度变化等许多领域中进行研究，并应用频率分析、小波变换及复系数方程等求解方法对波速求解[11-12]，迄今为止，压力波的研究仍在继续，领域扩展至储气库采气、钻井控压钻井、大跨越管道油气输送、非常规（页岩气、煤层气等）油气储层改造中.

川渝地区裂缝性地层具有出气不规律、出气量大的特点，井筒压力变化较为迅猛，需要考虑自动化压井带来的自动监控、控制作用，目前自动压井涉及压井方法的选择、复杂多相流的求解等难点，自动压井技术尚不成熟，仍需进一步研究.尽管前人对水平管道波速的研究很详尽[13-15]，但目前尚没有针对自动压井相关环空压力波速的研究.由于压力波速影响井底压力的响应时间，压力波沿环空传播的相长是调节节流阀时间间隔的重要判断依据，本文分析了自动压井过程中回压产生的压力波沿环空传播变化特性，可使压井工程师更直观地了解压力波传播速度以及传播影响的敏感因素，为川渝裂缝性地层实时压井提供帮助.

1 环空压力波速模型建立

1.1 环空控制体多相流模型建立

在环空中求解环空的压力波速，首先需要求解环空气相空隙率、环空压力、环空中气液两相密度等基础参数，作为压力波速求解的初始条件.因此，首先建立环空控制体多相流模型.

环空中取一控制体，气液连续数学模型[4]如下所示：

式中，A为环空截面积； ρk为气或钻井液相密度； φk为气/钻井液相的体积分数；vk为气或钻井液相速度；k为气/钻井液相；t为时间；s为环空长度.

式中，vsl，vsg分别为钻井液相及地层气相的表观速度，m/s；φl为持液率；φg为空隙率；∆s为控制体长度，m；∆t为微元时间，s；ρl为混相密度，kg/m3；p为压力，MPa.

1.2 压力波速双流体数学模型建立

建立环空气相质量守恒方程：

建立环空液相动量守恒方程：

经过小扰动变换，可得到

2 模型求解流程

2.1 环空压力多相压力波速求解思路

将环空离散成n个网格单元，对每个离散单元i分别利用半显式差分的方法求解多相流模型，获得环空多相流空隙率、气液密度、气体滑脱速度等参数；将每个单元i的多相流基础参数代入双流体数学公式（25），得到离散单元i的压力波速（具体求解技术路线如图1 所示）.求解步骤如下：

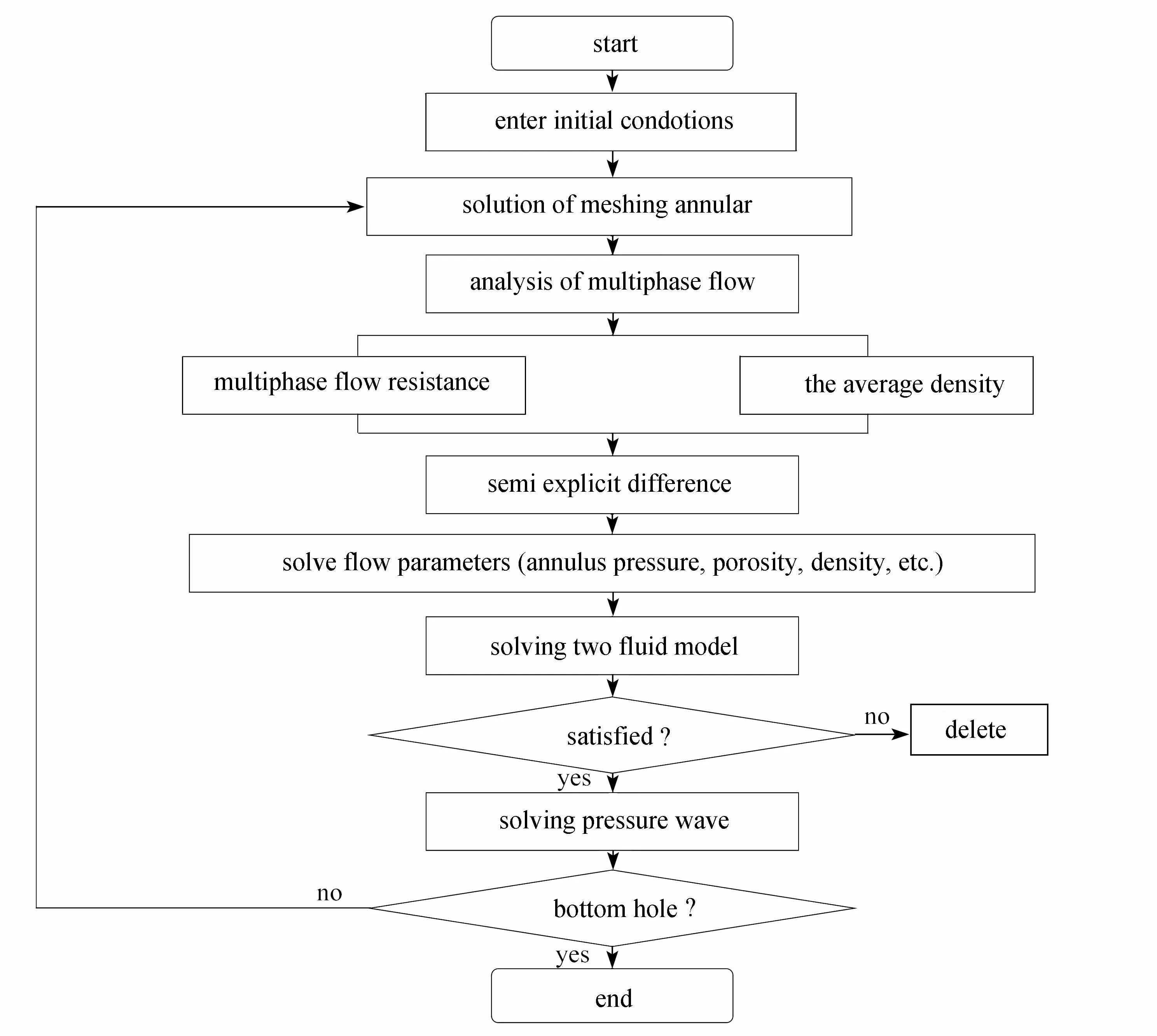
图1 环空多相压力波速求解技术路线图Fig. 1 The flowchart for solving the multiphase pressure wave velocity in annulus

第1 步 获取环空多相流中压力、空隙率、气相密度、液相密度、气体滑脱速度等参数；

第2 步 装双流体压力波速模型计算模块；

第3 步 按照网格顺序，获取压力波速.

2.2 压力波速模型验证

考虑虚拟质量力、环空沿程压力、相间阻力、气体滑脱、环空空隙率等因素，计算机编程求解了环空双流模型，分别对比了压力为30 MPa[15]及含气率在1%及20%条件下[16]前人实验实测的压力波速（图2），通过对比，编程求解的压力波速与前人实验测试数据具有一致性.

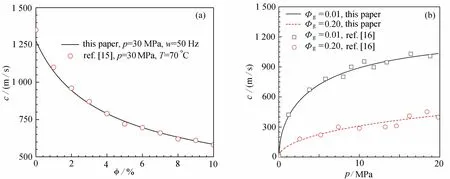
图2 文献[15-16]的实验测试结果与本文模型计算压力波速对比：（a）30 MPa 压力条件下压力波速对比结果；（b）含气率在1%及20%条件下波速对比结果Fig. 2 Comparisons between the experimental results of ref. [15-16] and the wave velocities calculated in this paper: (a) comparison of the wave velocity at a pressure of 30 MPa; (b) comparison of the wave velocity at gas contents of 1% and 20%

3 环空压力波速变化规律分析

PZ-5-3D 井位于四川省成都市彭州市葛仙山镇，完钻层位：雷四段TL43-3 层，靶点储层顶垂深5787 m、储层底垂深5827 m（如图3 所示），地质条件复杂，上下地层压力系数差别大，须家河组-小塘子组高压裂缝性气层发育（典型裂缝性地层），分布广，显示活跃且能量大，小塘子组气层活跃，钻至5600 m 发生溢流，钻井液黏度为0.056 Pa·s，钻井液密度为1.66 g/cm3，套管管柱弹性模量为2.07 × 1011，地面大气压为0.1 MPa，段塞流气泡平均宽度为0.002 m，裂缝地层出气量为0.33 L/s，BPT 节流循环排气回压，SPT 为立管压力.

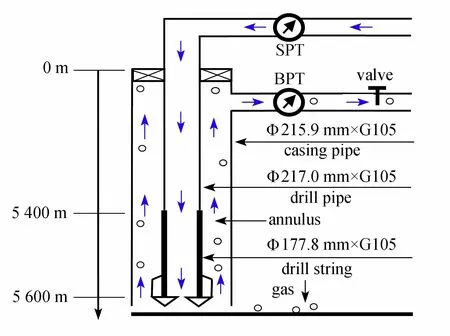
图3 自动压井气侵循环排气示意图Fig. 3 Schematic diagram of automatic well killing gas invasion circulating exhaust

3.1 裂缝气段塞流空隙率对压力波速影响

图4 为裂缝性地层出气，环空段塞流空隙率对压力波速的影响.随着压井环空压力波速增大，井底压力响应时间减小，节流阀调节时间间隔减小.流体弹性特点决定了流体的压缩性、气液能量耗散程度，从而影响压力波传递速度.随空隙率增大，压力波速呈现先减小后增大的趋势；裂缝气出气具有环空呈现段塞流流型特点，环空空隙率在0%至16%区间同16%至82%区间比较，压力波速变化幅度大.环空空隙率在0%至16%区间，流体主要以液相弹性为主，压力波速呈现急剧下降趋势；空隙率在16%至45%区间，流体主要以气相弹性-液相弹性为主，压力波速趋于恒定值；环空空隙率在45%至70%区间，流体主要以气相弹性为主，压力波速呈现增大趋势；环空空隙率大于70%区间压力波速区域稳定.

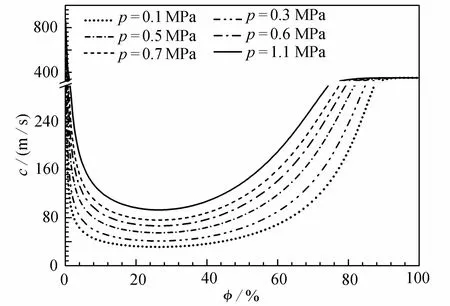
图4 裂缝气段塞流空隙率对压力波速的影响Fig. 4 Effects of the crack gas slug flow void fraction on the pressure wave velocity

3.2 裂缝性气侵速度对压力波速影响

图5 为裂缝性地层气侵流量v=0.01 L/s，0.08 L/s，0.15 L/s，0.22 L/s，0.29 L/s，0.33 L/s 条件下，压力波速沿环空变化特性分析.随环空空隙率减小，压力波速整体呈现减小趋势；当井底气侵流量增大时，环空整体空隙率也呈现增大趋势，压力波速呈现降低趋势，各井段压力响应时间延长，压井节流阀调节间隔增大.当气侵量较小时，在小于等于721 m 井深时，压力波速急剧增大，从132 m/s 增大至958 m/s；当气侵流量较大时，环空遭受气侵程度较大，压力波速沿着整个环控段呈现线性增大趋势，井底压力响应呈现减小趋势，节流阀调阀时间间隔呈现减小趋势.

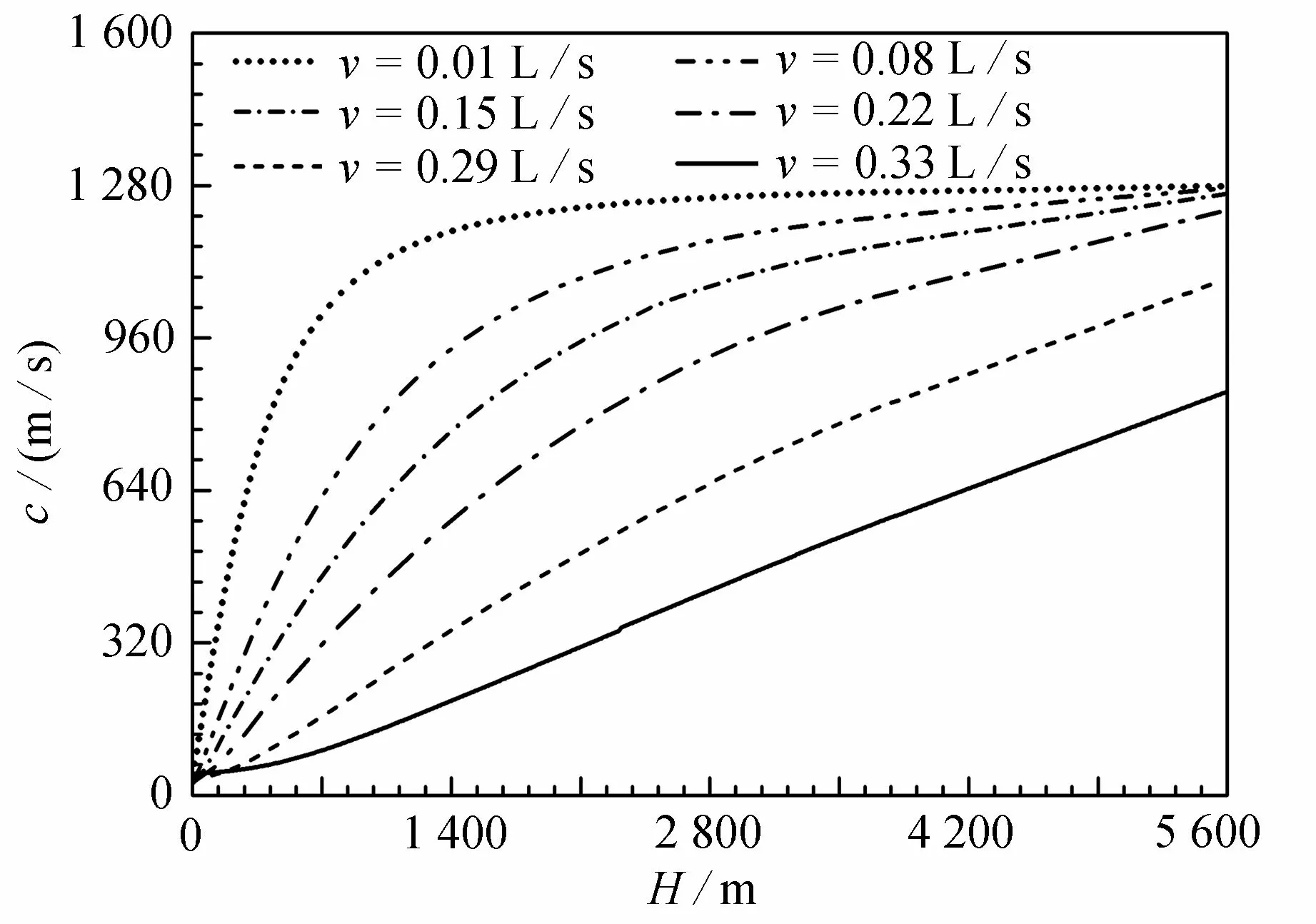
图5 裂缝性地层气侵流量对压力波速的影响Fig. 5 Effects of the gas invasion velocity on the pressure wave velocity in the fractured gas reservoir

3.3 压井节流阀回压对压力波速影响

图6 为压井节流阀回压（pBP=0.1 MPa，1.0 MPa，2.0 MPa，3.0 MPa，4.0 MPa，5.0 MPa）对压力波速的影响.当井底发生溢流时，自动压井系统依靠井口节流阀产生的实时回压循环排气，达到平衡井底压力的目的；随井口回压增大，压力波速整体呈现增大的趋势.回压的增大，增大了环空流体的平均压力，从而密度增大，减小了气液界面间动量、能量传递的损失，加大了气液相间的动量交换，从而压力波速呈现增大趋势.

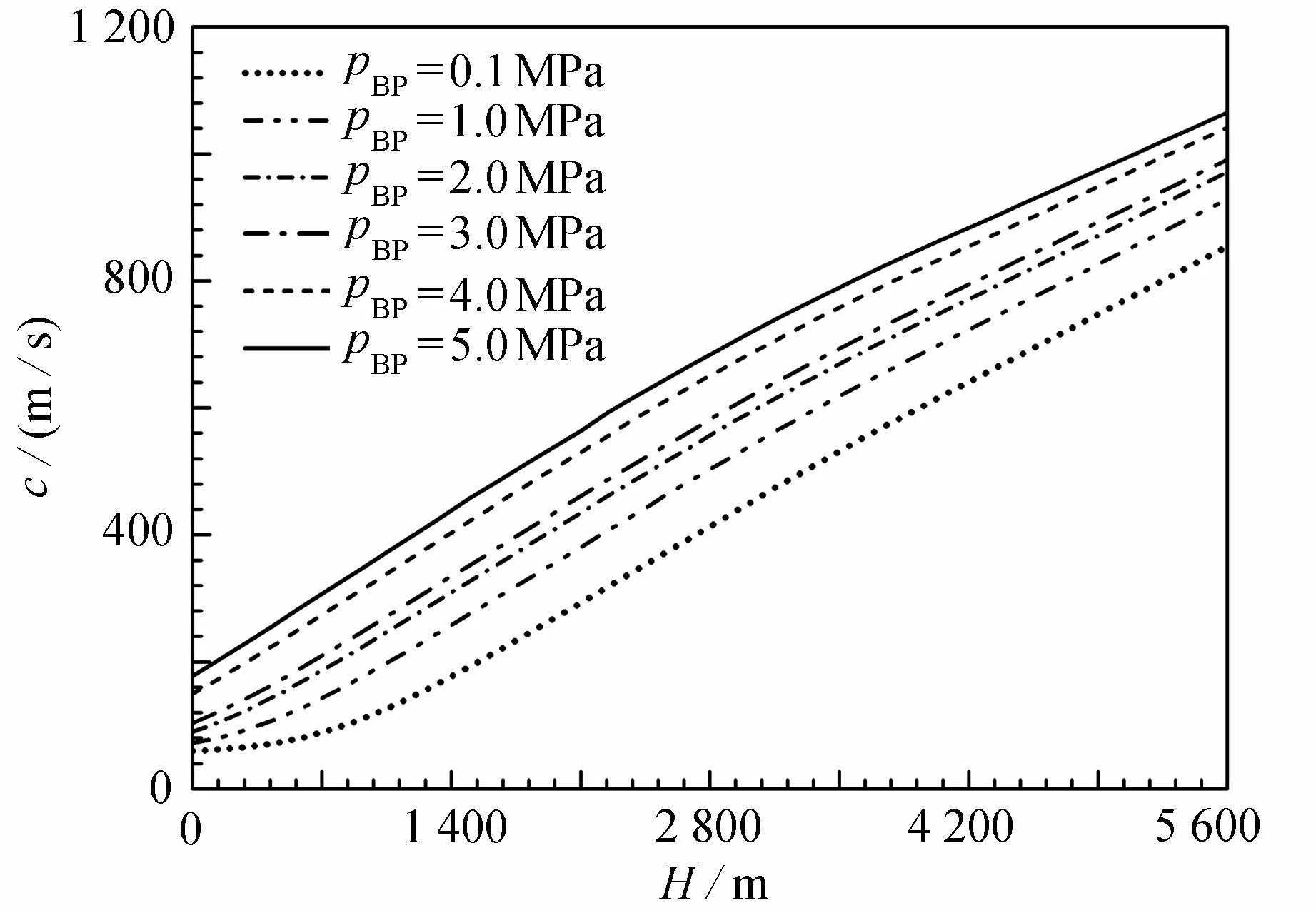
图6 压井节流阀回压对压力波速的影响Fig. 6 Effects of the throttle valve back pressure on the pressure wave velocity

3.4 角频率对压力波速影响

图7 为角频率(w=50 Hz，150 Hz，250 Hz，350 Hz，450 Hz，550 Hz)对压力波速的影响.很多工程类问题都选择了压力波速经验法求取压力波速，由于经验法求取压力波速忽略了角频率因素的影响，自动压井频繁调阀，会周期性产生压力波，如不考虑角频率，压力波速计算结果会产生一定误差.随角频率的增大，压力波速逐渐增大；当角频率到达高频段时，随角频率增大，减小了气液界面间动量、能量传递损失，加大了气液相间的动量交换，从而压力波速呈现增大趋势.

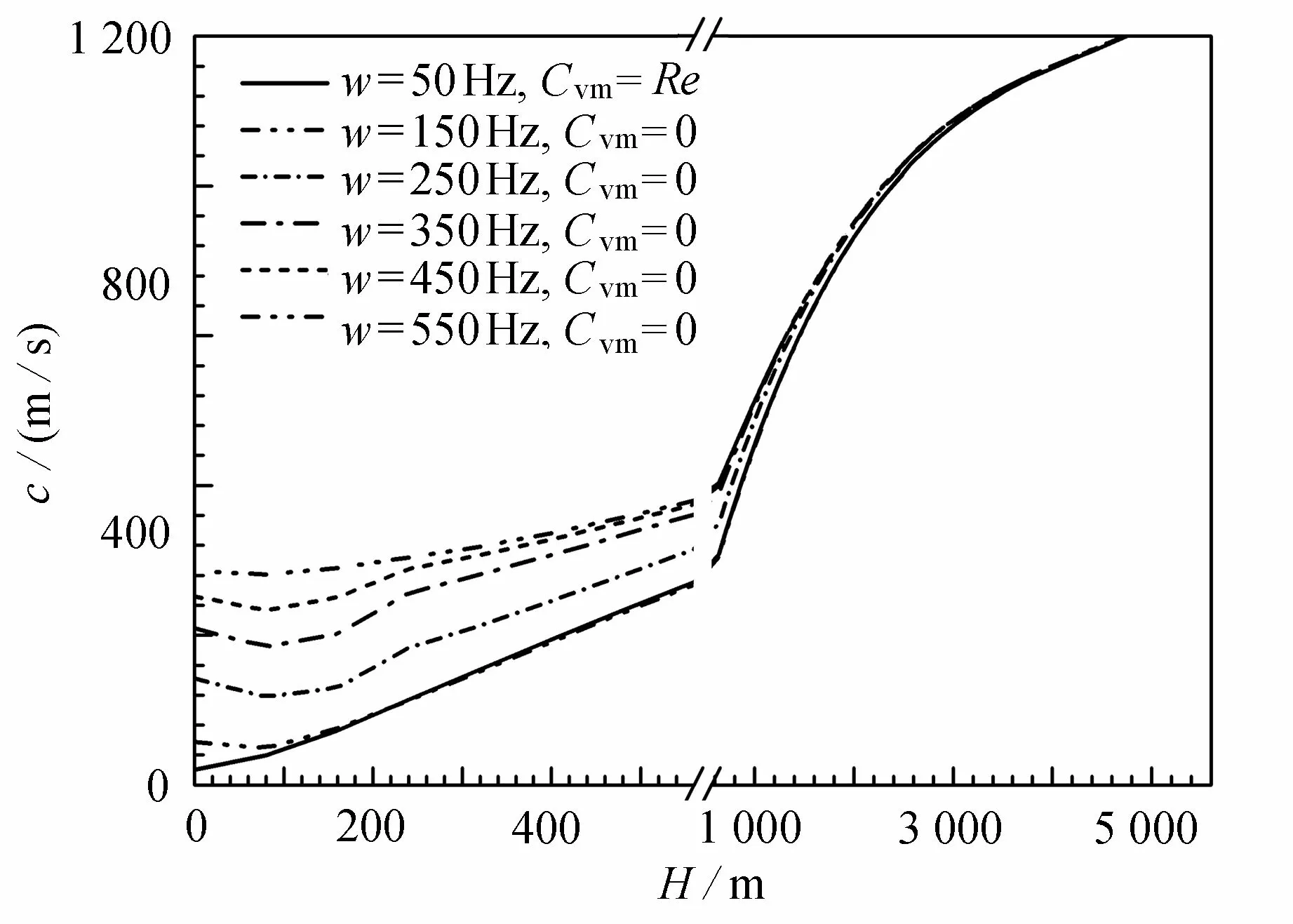
图7 角频率对压力波速的影响Fig. 7 Effects of the angular frequency on the pressure wave velocity

3.5 气体滑脱速度对环空压力波速影响

图8 示出了气体滑脱速度（vs=0.08 m/s，0.2 m/s，0.4 m/s，0.6 m/s，0.7 m/s，0.8 m/s）对环空压力波速的影响，不考虑虚拟质量力时，空隙率在0%至13%区间内，气体滑脱速度对压力波速影响不大；当气体滑脱速度为0.8 m/s 时，空隙率在13%至85%区间内，压力波速由42.5 m/s 增至320 m/s，随气体滑脱速度增大，压力波速呈减小趋势.考虑虚拟质量力时，空隙率在13%至85%区间内，压力波速呈现平缓恒定趋势；在压井环空中，考虑虚拟质量力与不考虑虚拟质量力相比，压力波速从40 m/s 增至290 m/s，增大了6.25 倍.

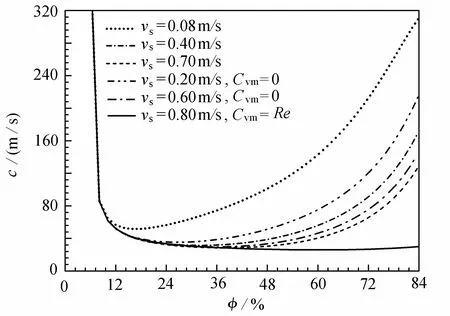
图8 气体滑脱速度对压力波速的影响Fig. 8 Effects of the gas slippage velocity on the pressure wave velocity

表1 为气体滑脱速度对压力波速影响数据表.在少量含气率的条件下，由于流体介质主要以液相为主，虽然气体滑脱速度增大，但对气液两相平均体积、平均密度影响不大，此阶段气体滑脱对压力波速的影响不大.当气体含量大于13%时，气体滑脱速度开始对压力波速产生影响，这是由于气体沿着环空向井口运移过程中，气体滑脱速度的增大，使得气体膨胀体积更大，此阶段气体体积对气液平均密度、环空压力影响逐渐增大，因此，此阶段气体滑脱对压力波速的影响逐渐增大.当含气率为98.1%时，滑脱速度0.8 m/s 同0.08 m/s 比较，压力波速从87.31 m/s 增大至349.99 m/s，压力波速增大了262.68 m/s，同87.31 m/s 比较，增大了200.86%.

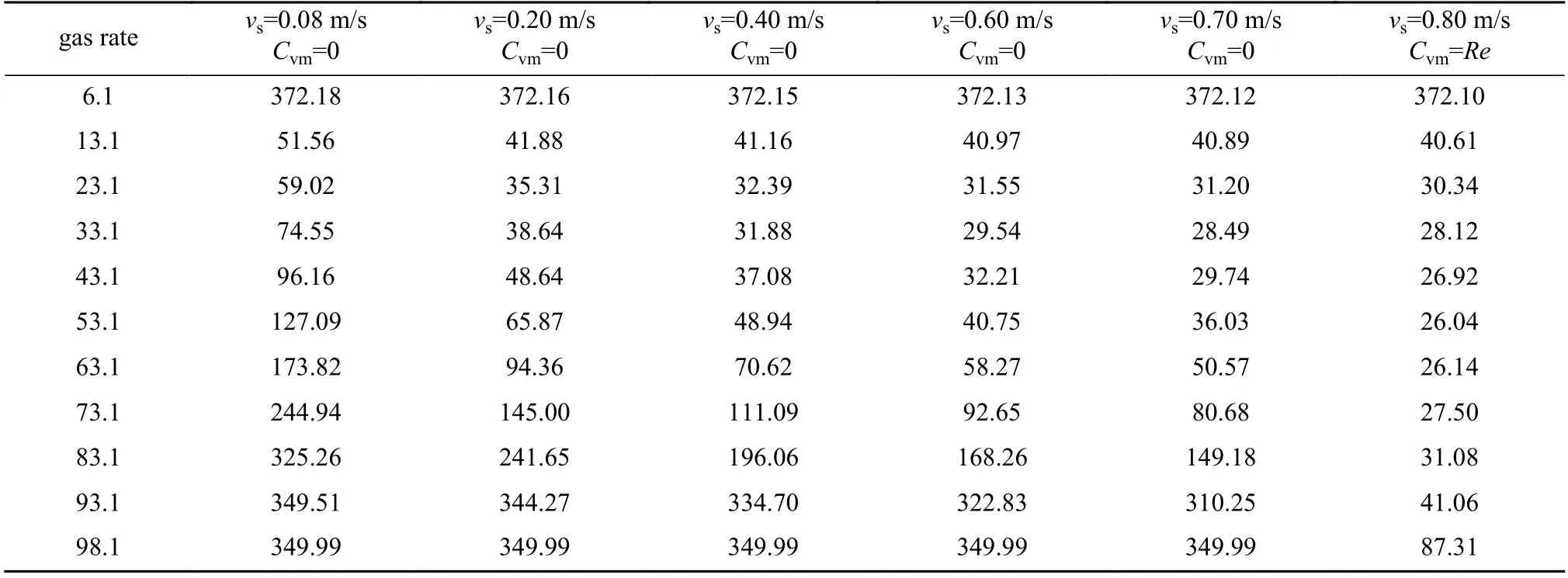
表1 气体滑脱速度对压力波速影响数据表Table 1 Effects of the gas slippage velocity on the pressure wave velocity

4 结 论

本文以川渝地区裂缝性地层气侵自动压井为背景，结合压井节流阀动作产生的压力波动源，分析了沿环空多相流动方向的压力波速变化特性，主要得到以下结论：

1） 由于裂缝气地层出气比较迅猛，环空多相流流型主要考虑段塞流流型；环空空隙率在0%至16%区间，压力波速呈现急剧减小趋势；环空空隙率在16%至45%区间，压力波速呈现增大趋势；环空空隙率在45%至70%区间，压力波速呈现增大趋势；环空空隙率大于70%区间，压力波速趋于稳定.

2） 与常规油气输送管道比较，压井循环排气过程中，压力波速计算不仅要考虑环空中时刻变化的空隙率、节流阀动作产生的回压值、气体滑脱速度、环空深度等因素，也要考虑虚拟质量力的因素，在压井环空中，考虑虚拟质量力与不考虑虚拟质量力相比，压力波速增大了6.25 倍.

3） 在压井循环排气操作中，节流阀频繁动作产生回压，达到控制环空循环排气的目的，从而平衡井底压力；节流阀动作间隔需要考虑压力波动的传播周期，压井工程师应尽量控制节流阀动作产生的稳态回压周期大于压力波沿环空传播一个周期时间，随压井环空压力波速增大，井底压力响应时间减小，节流阀调节时间间隔减小.

参考文献（ References ） ：

［1］ 姜海龙, 朱培旺, 徐东华. 考虑气体加速效应的高压气井产能方程推导及其应用[J]. 应用数学和力学, 2020, 41（2）:134-142. （JIANG Hailong, ZHU Peiwang, XU Donghua. Derivation and application of productivity equations for high-pressure gas reservoirs with gas acceleration effects[J].Applied Mathematics and Mechanics, 2020, 41（2）:134-142.（in Chinese））

［2］ 伍贤柱, 胡旭光, 韩烈祥, 等. 井控技术研究进展与展望[J]. 天然气工业, 2022, 42（2）: 133-142. （WU Xianzhu, HU Xuguang, HAN Liexiang, et al. Progress and prospect of well control technology research[J].Natural Gas Industry, 2022, 42（2）: 133-142.（in Chinese））

［3］WILLIAM B.Consideration of Compressibility Effects for Applied-Back Pressure Dynamic Well Control Response to a Gas Kick in Managed Pressure Drilling Operations[M]. Master of Science in Mechanical Engineering,The University of Texas at Arlington, 2011.

［4］ 史爽, 敬加强, 孔祥伟. 大跨越管道油气混输压力波速及响应特性研究[J]. 应用数学和力学, 2016, 37(3): 290-300.（SHI Shuang, JING Jiaqiang, KONG Xiangwei. Research of pressure wave velocity and response time for oil-gas mixing transportation in large span pipelines[J].Applied Mathematics and Mechanics, 2016, 37（3）: 290-300. （in Chinese））

［5］ 刘磊, 王跃社, 周芳德. 气液两相流压力波传播速度研究[J]. 应用力学学报, 1999, 16(3): 22-27, 150-151. （LIU Lei,WANG Yueshe, ZHOU Fangde. Propagation speed of pressure wave in gas liquid two phase flow[J].Chinese Journal of Applied Mechanics, 1999, 16（3）: 22-27, 150-151. （in Chinese））

［6］ 黄飞, 白博峰, 郭烈锦. 水平管内气液两相泡状流压力波数学模型及其数值模拟[J]. 自然科学进展, 2004, 14（4）: 344-349. （HUANG Fei, BAI Bofeng, GUO Liejin. Mathematical model and numerical simulation of pressure wave in gas-liquid two-phase bubble flow in horizontal tube[J].Progress in Natural Science, 2004, 14（4）: 344-349.（in Chinese））

［7］ 白博峰, 黄飞, 王先元. 气液两相流压力波色散特性实验研究[J]. 工程热物理学报, 2005, 26（3）: 447-450. （BAI Bofeng, HUANG Fei, WANG Xianyuan. Experimental study on pressure wave dispersion characteristics of gas-liquid two-phase flow[J].Journal of Engineering Thermophysics, 2005, 26（3）: 447-450.（in Chinese））

［8］ 王海成. 天然气井压井与带压施工的实践与认识[J]. 中国石油和化工标准与质量, 2021, 41(10): 144-145. （WANG Haicheng. Practice and understanding of natural gas well killing and pressure construction[J].China Petroleum and Chemical Standards and Quality, 2021, 41（10）: 144-145. （in Chinese））

［9］SUROSO T, TRIYOSO W, PRIYONO A. Hydrocarbon identification by evaluating anisotropy parameters estimated from crosswell seismic data[J].Journal of Physics:Conference Series, 2021, 1943（1）: 12030-12038.

［10］ 袁凡, 吴望一. 脉象的血管位移波理论[J]. 应用数学和力学, 1989, 10（6）: 469-476. （YUAN Fan, WU Wangyi. The displacement wave theory of blood vessel[J].Applied Mathematics and Mechanics, 1989, 10（6）: 469-476.（in Chinese））

［11］ 刘小靖, 周又和, 王记增. 小波方法及其力学应用研究进展[J]. 应用数学和力学, 2022, 43（1）: 1-13. （LIU Xiaojing,ZHOU Youhe, WANG Jizeng. Research progresses of wavelet methods and their applications in mechanics[J].Applied Mathematics and Mechanics, 2022, 43（1）: 1-13.（in Chinese））

［12］ 卫志军, 申利敏, 关晖, 等. 拓扑优化技术在抑制流体晃荡中的数值模拟研究[J]. 应用数学和力学, 2021, 42（1）: 49-57. （WEI Zhijun, SHEN Limin, GUAN Hui, et al. Numerical simulation of topology optimization technique for tank sloshing suppression[J].Applied Mathematics and Mechanics, 2021, 42（1）: 49-57.（in Chinese））

［13］MEHRDAD K, ABDORREZA K, MOHAMMAD N S, et al. Investigating the effects of transient flow in concrete-lined pressure tunnels, and developing a new analytical formula for pressure wave velocity[J].Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2019, 11（91）: 18-25.

［14］MOSLAND E N, LOHNE K D, YSTAD B, et al. Pressure wave velocity in fluid-filled pipes with and without deposits in the low-frequency range[J].Journal of Hydraulic Engineering, 2018, 144（10）: 101-106.

［15］LIU X, LI B, YUE Y. Transmission behavior of mud-pressure pulse along wellbore[J].Journal of Hydrodynamics, 2007, 19（2）: 236-240.

［16］ 李相方, 管丛笑, 隋秀香, 等. 压力波气侵检测理论及应用[J]. 石油学报, 1997, 18（3）: 128-133. （LI Xiangfang,GUAN Congxiao, SUI Xiuxiang, et al. The theory of gas influx detection of pressure wave and its application[J].Acta Petrolei Sinica, 1997, 18（3）: 128-133.（in Chinese））