基于期权价值状态的股市预测模型分析
2022-01-29张艺


摘 要:期权在整个资本市场中占据着重要地位,本文在经典的Black-Scholes公式理论框架下,以上证50ETF指数、中国一年期国债历史收益率等数据为研究对象,通过Python计算和可视化等技术,构建交易策略,实证检验了基于期权价值状态的股市预测模型。发现无论是定投ETF基金的当前收益率还是累计收益率,对整个策略到期收益率的解释程度都不高,存在定投标的资产无法解释的收益率。
关键词:上证50ETF指数;期权定价策略;隐含波动率;Black-Scholes模型;到期收益率
本文索引:张艺.<标题>[J].商展经济,2022(03):-099.
中图分类号:F830.9 文献标识码:A
1 项目背景
期权在整个资本市场中占据着重要地位,与期货、现货相互配合,完善了金融市场的风险管理体系。我国期权市场发展较晚、品种较少、成熟度较低,对国内期权的相关研究起步也较晚。直到2015年2月9日,在经过一年多的模拟测试后,上证50ETF期权才在上海证券交易所上市,经过一年多的稳健发展,这一合约品种交易越来越活跃,参与的市场投资者也越来越多,在这样的背景下,对国内期权市场的研究和预测也变得越来越重要。
期权有实值、平值和虚值三种价值状态。实值状态意味着立刻行权即可获得正收益,平值状态意味着立刻行权不赚也不亏,虚值状态意味着立刻行权将获得负收益。当市场处于带有泡沫的繁荣期时,资产估值虚高,同时投资者看多情绪也会高涨,往往导致虚值看涨期权的价值偏高(即市场普遍认为当前行权产生负收益的期权在未来行权会产生正收益),同时虚值看跌期权的价值偏低。
本文以期权的价值状态为指标构建交易策略,选取真实的市场数据,实证检验期权的价值状态并构建交易策略预测股市。
2 数据预处理与特征挖掘
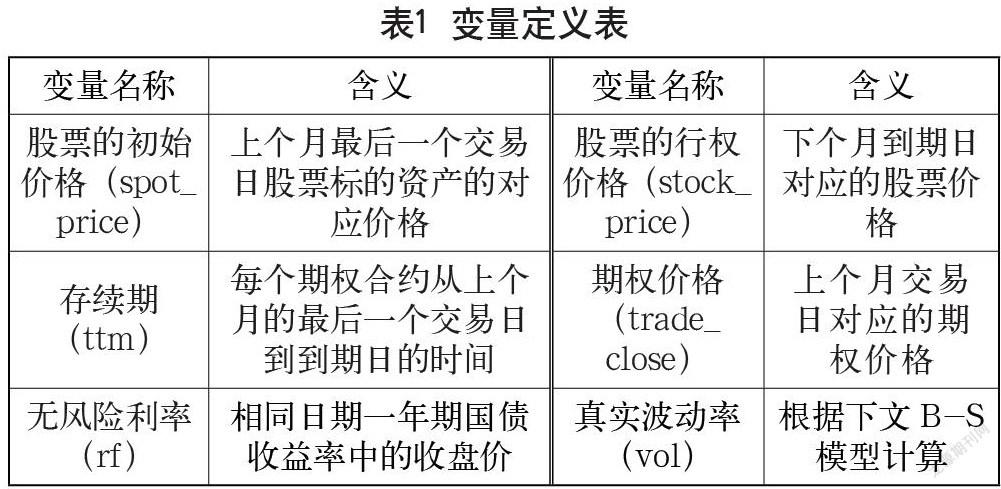
本文选取2015年3月—5月我国一年期国债收益率数据、华夏上证50ETF股票数据和华夏上证50ETF期权数据作为样本。其中,华夏上证50ETF期权历史数据中包括期权类型、行权价、发行日期、到期日和期权发行价。本文利用剩余两项数据获取包括无风险利率、股票当日价格和波动率在内的其他信息:首先,本文以相同日期一年期国债收益率中的收盘价作为该日期华夏上证50ETF期权的无风险利率(rf)。其次,本文从华夏上证50ETF股票历史数据中选取每个日期的前收盘价作为该日期期权所对应的股票初始价格(spot_price)。最后,通过股票历史数据中的涨跌幅,本文又计算了每个日期所对应的真实波动率(vol)。因为构建交易策略时,建仓和平仓分别是在最后一个交易日和下一个月的到期日完成,以期权合约在每月最后一个交易日与到期日的价格数据分别作为即期价格和行权价格。
具体的变量定义如表1所示。
上交所有上证50ETF期权和沪深300ETF期权两类期权合约。其中,上证50ETF期权在2015年已上市交易,而沪深300ETF期权在2019年才上市交易,样本量相对较少,分析结果可能有偏差,参考已有研究剔除沪深300ETF期权数据。同时,考虑到数据的有效性,本文只保留2020年5月之前到期且存续期大于30天的期权合约。
最终本文选取2015年3月—5月上证50ETF期权共62个交易数据作为研究样本。
3 构建实值期权对冲交易策略
自上证50ETF期权上市交易开始,上个月的最后一个交易日建仓,如果当日实值看涨期权的平均隐含波动率大于实值看跌期权的平均隐含波动率,说明看涨期权合约整体相对被高估,看跌期权合约整体相对被低估。因此,买入所有实值看跌期权,同时卖出所有实值看涨期权,构建对冲交易策略。每个月的到期日平仓,交割所有到期的期权合约,隐含波动率指标蕴含着投资者对后市判断的主观信息。针对每一个到期日做一个建仓和平仓操作,每一期都构建一个交易策略,看整体的表现。
3.1 计算隐含波动率
隐含波动率是将市场上的期权交易价格代入Black-Scholes期权理论定价模型(以下简称B-S模型),反推出来的波动率,是一个重要的風险指标。历史波动率反映期权标的证券在过去一段时间的波动幅度,期权发行商与投资者在期权发行初期只能利用历史波动率作参考。一般来说,期权的隐含波动率越高,隐含的风险也就越大。期权投资者除了可以利用期权的正股价格变化方向来买卖权证外,还可以从股价波动幅度的变化中获利。一般来说,波动率并非无限上涨或下跌,而是在一个区间来回振荡,投资者可以通过在隐含波动率较低时买入,在较高时卖出来获利。
B-S模型的基本思路是构造一个无风险且无套利机会的股票加期权的投资组合(Black and Scholes,1973)。首先,模型构建无风险投资组合,即无论股票价格未来如何变动,投资组合的未来收益是确定的。其次,模型进行无套利定价,即投资组合的未来收益率等于市场的无风险利率(见表2),基于B-S模型的欧式看涨期权价格由下式给出:
由上述公式可知,B-S定价模型对看涨期权的定价计算可用公式(1)表示,对看跌期权的定价计算可用公式(2)表示。其中,N(d1)和N(d2)为d1与d2的正态累积分布函数。
3.2 构建模型
本文选取2015年3月—5月交易日期权合约的数据建立隐含波动率模型。隐含波动率是期权的市场价格中所包含的波动率,即由期权价格和期权定价公式反推的波动率。隐含波动率和历史波动率作比较,可以指导投资者的操作,故交易员非常关心。投资者可以直接买卖波动率,或者参考波动率确定买卖时机。
3.3 策略比较可视化分析
3.3.1 策略当前收益率与上证50ETF基金同期收益率比较
相较于定投50ETF基金的同期收益率(fund returns),期权策略当期收益率(option strategy returns)的整体表现比基金好得多,但其波动率很大。从图1可知,最高一期(不到30天)的收益能超过50%,最差的时候一期就会亏掉70%的本金,可以看出,期权策略的收益和风险远大于股市投资。
3.3.2 策略累积收益率与上证50ETF同期收益率比较
从策略累积收益率可以看出,期权策略的风险远大于定投标的资产的风险。如图2所示,期权策略的回撤非常明显,可以从350倍的收益直接回撤到十几倍,幅度非常大。做期权策略投资的时候要注意,如果确信期权策略有盈利空间,就要避免由于前期表现不好而放弃的行为,一旦抓住机遇,盈利空间就非常可观。
4 期望假设回归分析
期望假设回归分析是回归分析的变种,是在做回归分析的时候提出显著性假设,构建线性回归方程。基于此,对option strategy returns和fund returns做期望假设回归分析。期望假设回归分析的目的在于判断fund_profit能否解释收益率的变动,以及能在多大程度上解释。
4.1 当期收益率期望假设回归分析
通过调用Python库statsmodels拟合多种统计模型,执行统计测试及数据探索和可视化。使用OLS(普通最小二乘模型)进行建模,回归结果如表3所示。
收盘价系数是3.532,显著不为1,R-squared和Adj.R-squared反映数据对模型的解释程度,故数据对模型有大约11%的解释程度,解释程度不是非常理想。
4.2 到期收益率期望假设回归分析
通过调用Python库numpy的cumprod累积函数处理数据,OLS进行建模,回归结果如表3所示。
数据对模型有23%的解释程度,且解释变量无论是系数大小还是显著性均有明显提高。无论是定投ETF基金的当前收益率还是累积收益率,对整个策略到期收益率的解释程度都不是特别高,同时变动幅度都不是1∶1,说明策略有定投标的资产无法解释的收益率,策略捕捉到独一无二的与标的资产不相关的市场盈利空间,这就是做期望假设回归分析的目的。
5 其他策略
5.1 虚值期权构建策略
如图3所示,选取虚值期权构建交易策略得到当期收益率。
如图4所示,分析累期收益率。fund returns依旧是一条曲线,option strategy return只有一个点。
从图5可以看出,第一个数值ret_cat=2.6158,是正常的,第二个数值ret_cat=inf,表示这一期的收益是无限的。原因是做第二期期权的时候成本为0,则收益无限大,但依旧承担风险,接近套利行为,产生极高的正收益。往后看出现ret_cat=-1,表示本金亏完,收益为0。这就是构建期权策略需要承担的风险。如果期权仓位都是多头,存在亏光本金的风险;期权仓位存在空头,则会产生无法想象的亏损,损失无下限。因此,构建期权交易策略在取得高收益的同时,也面临着高风险。同时,虚值期权的交易风险大于实值期权。
5.2 所有期权构建策略
通过对所有期权进行拟合,得到如图6所示的当期收益率。
如图7所示,蓝色曲线option strategy return拟合出的到期收益率一直处于增长状态,在2020年前几个月,期权策略的效果非常好。
6 结语
综上所述,本文以上证50ETF指数数据、中国一年期国债历史收益率等数据为研究对象,通过Python计算和可视化等技术,验证基于期权价值状态的股市预测模型。通过基于期权价值状态的分析,得出以下结论:
(1)合约价值状态的改变,从实到虚会大大增加亏损幅度。
(2)趋势判断错误,若合约处于虚值状态,则应果断止损,择机再进场。
(3)虚值状态的合约进一步虧损时,不要轻易补仓、加仓,期权投资没有传统股票的“摊低成本”之说,轻易加仓大概率会加大亏损。
(4)无论是定投ETF基金的当前收益率还是累积收益率,对整个策略到期收益率的解释程度都不高。
(5)本文策略模型预测存在着定投标的资产所无法解释的收益率,策略捕捉到与标的资产不相关的市场盈利空间。
参考文献
BLACKF, SCHOLESMS. The pricing of options and corporate liabilities[J]. Journal of Political Economy, 1973, 81(3): 637-654.
姜晓晴.上证50ETF期权定价研究:基于B-S模型与CEV模型[J].吉林工商学院学报,2020,36(3):64-70+75.
李柔昊,尹航.上证50ETF期权在套期保值中的应用实证分析[J].商展经济,2020(6):55-60.
吕雪岭,熊熊,严雨萌,等.“稳定”还是“扰动”:基于上证50ETF期权的实证分析[J].管理科学,2020,33(4):149-157.
郁瑞澜,商豪.基于随机波动率模型的沪深300ETF期权定价[J].湖北工业大学学报,2021,36(4):116-120.
张益敏,王献东.上证50ETF波动率的研究[J].现代营销(学苑版),2021(8):34-35.
赵阳.上证50ETF波动率的实证研究[D]. 北京:北方工业大学,2017.
郑振龙,汪饶思行.隐含波动率曲面的建模与预测[J].当代财经,2017(3):48-60.
