基于多传感器信息融合的异步点迹关联方法

刘静涛 路 娜 周君会

1(91977部队 北京 100036) 2(西安电子科技大学通信工程学院 陕西 西安 710071)

0 引 言

基于多传感器的信息融合系统充分利用了各个传感器的信息资源，通过各传感器之间信息互补来发挥各传感器的性能优势，通过将多个传感器的信息进行关联、融合等多级处理来获得更加精确的点迹信息，使得多传感器系统能够更加高效稳定的工作。

点迹关联的目的是找到各个传感器中来自同一个目标的局部点迹。基于统计学，文献[1]和文献[2]将加权法应用于点迹关联中；Bar-shalom等[3-5]通过改进加权算法提出了修正法；Kosaka等[6]提出了最近邻(Nearest Neighbor,NN)算法；何友等[7-8]对最近邻算法进行改进，提出了KNN和MKNN算法。然而当目标数目比较密集或者误差较大时，统计学算法关联的效果明显下降。

由于不同传感器的原因，得到的往往是异步点迹。文献[9-11]提出了最小二乘法进行时间配准解决异步点迹关联。然而，通过时间配准解决异步点迹关联的方法会产生较大的估计误差，并会增加算法的复杂度，因此提出一种有效的异步点迹关联方法是非常有必要的。

本文基于分布式多传感器信息融合系统，主要对一般场景下的点迹关联以及异步场景下的点迹关联进行研究。在不进行时间配准的前提下，提出一种基于时间分段和提取趋势项的方法解决异步点迹关联问题。

1 点迹关联原理及流程

在不同的传感器系统下，由于各自的工作方式、参考坐标系、测量误差及采样速率等不同，生成的局部点迹相互独立。将不同传感器局部点迹数据转换到统一坐标系下并进行时间配准，通过预处理可提高目标跟踪精度。点迹关联处理流程如图1所示。

图1 点迹关联处理流程

在目前的研究中，一般方法是通过时间配准将异步点迹同步化，最常见的就是内插外推及最小二乘法时间配准的方法。在本文的研究中，传感器A和传感器B的采样速率是倍数关系，采用的方法是将采样速率比较快的传感器的量测数据统一到采样速率比较慢的传感器上，从而实现时间的同步化，完成时间配准。

2 异步点迹关联

在分布式传感器的点迹融合系统中，由于不同传感器不同的采样速率或者通信延迟，因此得到的往往是异步点迹。

在异步点迹关联的研究中，主要是将异步同步化。由于异步同步化计算量比较大，同时也会带来较大的计算误差，最终使得配准精度较低。本文提出一种基于时间分段和EEMD提取趋势项的方法解决异步点迹关联问题。首先将时间进行分段，在每一个时间段内，用EEMD方法提取趋势项，然后用最小二乘法的方法拟合该趋势项的表达式，根据多项式系数的统计检验结果进行关联判断以进行异步点迹关联。异步点迹关联的模型如下：传感器A和传感器B在一个周期内获得N个目标的异步点迹。传感器A在第k个周期内的点迹集合为：

(1)

(2)

图2 异步点迹不同速率采样示意图

2.1 异步点迹关联的一般方法

异步点迹传统方法是通过时间配准的方法将异步同步化，基本流程如图3所示。

图3 传统的处理异步点迹方法基本流程

2.1.1基于最小二乘法的异步点迹关联算法

(3)

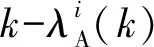
(4)

(5)

传感器A点迹i的所有点的真实状态量为:

(6)

(7)

令:

(8)

(9)

(10)

(11)

在k时刻的估计误差为：

(WA(k)TWA(k))-1WA(k)TVA(k)

(12)

2.1.2基于点迹重构的异步关联算法

点迹重构就是统一不同时刻的状态估计值和点迹滤波值到同一时刻上，当所有点迹都重构到相同的时间点上，就完成了时间配准，如图4所示。

图4 基于点迹重构的异步关联算法结构

将传感器A和传感器B在Tk前后时刻的估计值外推到Tk时刻。传感器A和传感器B在Tk时刻的估计值为X1(Tk,Tk)和X2(Tk,Tk)。点迹目标j的状态方程为：

(13)

(14)

(15)

(16)

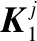
(17)

(18)

(19)

(20)

2.2 基于分段趋势项提取的异步关联算法

本文提出了一种基于时间分段和基于集合经验模态分解(EEMD)提取趋势项的异步关联。该算法的整体框架如图5所示。

图5 基于分段趋势项提取的异步点迹关联框架

(1)时间分段。在获得传感器的点迹集合内，如果直接进行趋势项提取，计算量很大。如果多项式是低阶的，得到的曲线会过于粗糙，明显降低关联效果。由于在每一小段时间内，目标可以视为做加速运动，因此用二阶多项式表示即可。采取的思想是：根据不同传感器的异步采样速率，确保每一段时间内，两个传感器的起止时刻相同或者相似。一个简单的时间分段如图6所示。

图6 时间分段

白色和黑色分别代表传感器1和传感器2，采样步长分别设置为2和3。T1,T2,T3,T4,T5,…代表不同传感器的相同的采样时刻，每两个采样相同的时刻可以作为一个时间段。首先将点迹集合进行时间分段，然后在每一个时间段内，采用上述方法进行异步关联。

(2)趋势项提取。趋势项的定义为[12]：信号中周期大于采样长度的频率部分。在EEMD提取趋势项中，如果分解的IMF分量满足该定义，则满足条件的IMF分量(一般是低频的IMF分量)和余量之和就可以作为趋势项。如果直接将余量作为趋势项，则提取的精度低，影响关联的效果。通过提取趋势项再进行曲线拟合的方法减小了高频项作为噪声扰动的影响，通过趋势项的提取，使序列相对平稳，因此多项式的阶数不需要设置为高阶，本文将多项式的阶数设置为二阶。

(3)确定多项式系数。提取的趋势项作为新的点迹集合特征向量，在同步点迹关联中可以利用传统的点迹关联的方法进行关联。在异步点迹的关联中，对应的时间点不是对齐的，因此，不能利用传统的点迹关联方法。在每一段时间内，比较的是两个点迹集合对应的发展走势和形态，这种特征用一个二阶多项式表示出来。每一个提取趋势项的点迹集合看作一个二阶多项式，这个二阶多项式系数唯一。在一个时间段内，点迹集合i和点迹集合j如果有相同的发展趋势，则它们对应的多项式系数是接近的，可以通过接近程度判断是否相关。提取的趋势项用最小二乘法曲线拟合的方法来确定多项式的系数，然后对多项式的系数进行统计检验。

(4)最大似然值统计检验。用最大似然值统计检验的方法来比较多项式系数的接近程度，从而判断这两个多项式表达的点迹是否来自于同一个目标。用以下二阶多项式描述：

(21)

式中：kTi=[miTi,niTi]，miTi=Tk，niTi=Tk+1;lTj=[mjTj,njTj]，mjTj=Tk，njTj=Tk+1；ai表示点迹集合i要估计的二阶多项式系数；aj表示点迹集合j要估计的二阶多项式系数。

(22)

Hs=[fs(msTs),…,fs(nsTs)]Ts=i,j

(23)

θs=[as0,as1,as2]Ts=i,j

(24)

式中：[Tk,Tk+1]为第k个时间段；Ts表示两个传感器采样周期；ns-ms+1 (s=i,j)表示每个时间段内两个传感器的采样长度。利用最小二乘法可以得到：

(25)

Lij(x,k)=

(26)

Lij(x,k)、Lij(y,k)、Lij(z,k)就是X、Y和Z方向上在时间段[Tk,Tk+1]上的最大似然值。

(5)异步关联判断。根据上面得到的Lij(x,k)、Lij(y,k)、Lij(z,k)，进行如下异步关联判断：

Lij(k)=(Lij(x,k)>δ)∩

(Lij(y,k)>δ)∩(Lij(z,k)>δ)

(27)

式中：δ值为关联门限值，该值通过经验和实验进行设置。根据关联质量mij的判断，当满足式(27)关系时，mij加1。N0次关联检验中，如果超过K次满足该条件，则判断点迹i和j来自同一个目标。当不止一个点迹集合判断为关联时，考虑在每一个起止时刻一致的点或者时间差相差很小的时刻，可以利用多义性关联判断。

3 实验与结果分析

在各个点迹集合规律不同的场景且有一定的误差条件下，研究目标数目和关联正确率间的关系。

从第四个时刻开始，点迹i和j提取趋势项后采用最小二乘法拟合出二次多项式的表达式。通过算式a=polyfit(x,y,m)(MATLAB函数)求出多项式系数，其中x、y和m分别表示输入航迹序列的采样时间、点迹序列数据和拟合多项式的阶数，a中存储的即为二次多项式的系数。

传感器A和传感器B从同一时刻开始采样，但采样速率不相同，传感器A的采样速率为5 s，传感器B的采样速率为7 s。首先在一段长度为100的航迹片段内，在传感器A中选择了目标1的航迹点，在传感器B中分别选择了目标1和目标2的点迹点，其中目标1与传感器A的目标1是来自于同一个目标，并对这两个传感器的三个目标的点迹利用EEMD的方法提取趋势项，在X、Y和Z方向上对这三个目标的点迹集合和趋势项提取进行仿真，结果如图7所示。

图7 X、Y和Z方向上异步采样点和提取趋势项显示结果

可以看出，传感器A的目标1的趋势项和传感器B的目标1的趋势项最为接近，这是因为它们来自于同一个目标。

传感器A的采样速率为5 s，传感器B的采样速率为7 s，仿真中每35 s为一个时间段，且只考虑了不同传感器采样速率不同的情况，点迹总长度设置为350，在每一个时间段长度为35的情况下，将时间段数设置为10，将关联门限值设置为0.75。将本文算法与基于时间配准的KNN算法进行对比分析，两种算法的仿真结果如图8所示。

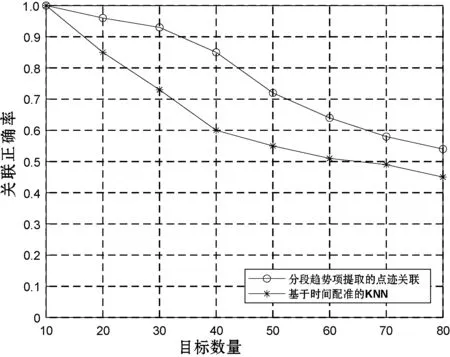
图8 异步关联点迹不规则情况下的对比

可以看出，在点迹不规则场景下，随着目标数目的增加，关联正确率下降，基于分段趋势项提取的异步关联整体关联效果好于基于时间配准后的KNN算法。当目标数目在30个以内时，分段趋势项提取的异步关联正确率保持在90%以上，然而随着目标数目再继续不断增加时，关联的正确率下降得也很快。因此，在目标数量适中的场景下，基于分段趋势项提取的异步点迹关联算法有较好的关联效果。

4 结 语

本文采用基于分段趋势项提取的异步点迹关联算法研究了异步场景下的点迹关联，对关联方法中的时间分段、趋势项提取、确定多项式系数，以及异步关联判断进行了具体分析，选取了基于时间配准的KNN算法与本文方法进行了对比，发现在目标数量适中的情况下，本文方法有较好的关联效果。在下一步的工作中，将提高方法的实用性，并提升系统的时效性。