高冲击载荷作用下平面式电涡流阻尼器特性数值模拟研究
2022-01-27高钦和刘志浩刘大伟
黄 通, 高钦和, 刘志浩, 刘大伟
(火箭军工程大学 导弹工程学院,西安 710025)
火炮、导弹等武器装备由于在发射过程中产生巨大的冲击载荷,不利于发射平台的稳定和射击精度的提高。传统的液体气压式制退机通过提供液压阻力制动可以达到平缓后坐力,降低后坐阻力峰值的效果,但是由于理论假设的近似性和制造装配误差的不确定性,结构较为复杂的液体气压式制退机难以达到理想后坐阻力曲线的平台效应,国内外研究学者针对这一问题,提出了多种技术方案[1]。
电涡流阻尼技术由于在阻尼产生过程中初级与次级不发生接触,具有磨损小、结构简单、便于控制等优点,在振动控制、桥梁建筑和列车制动等领域得到了广泛应用[2-5]。其中,陈政清等[6-8]建立了平面式电涡流阻尼器有限元模型,分析了各设计参数对阻尼比的影响;汪志昊等[9-10]基于性能测试和有限元分析,发展和完善了平面式电涡流阻尼器的磁路优化设计。电涡流阻尼技术在火炮后坐制动中的应用研究在国内也已经开展,但主要集中在圆筒形结构方面的研究,其中,李子轩等[11]研究分析了火炮发射载荷下圆筒形电涡流阻尼器的阻尼特性;黄通等[12]研究分析了圆筒型电磁阻尼器在冲击载荷作用下的动力学特性,但存在结构尺寸和质量过大的问题。
本文针对平面式电涡流阻尼器在发射冲击环境中的应用,建立了高冲击载荷作用下平面式电涡流阻尼器二维数值仿真模型,重点分析了永磁体和磁靴结构尺寸、导电层和导磁层厚度以及气隙间距对阻尼力的影响,进而探究了冲击环境中去磁效应现象的影响特性,研究结果可为平面式电涡流阻尼器在冲击环境中的应用提供支撑和参考。
1 数值仿真模型
1.1 物理模型
电涡流阻尼器的种类多样,按照结构形式区分一般可以分为圆筒式、圆盘式和平面式。某型平面式电涡流阻尼器物理模型如图1所示,该型平面式电涡流阻尼器属于被动式电涡流阻尼器,磁源为永磁体,主要是由定子板和动子块两部分组成,其中,定子板由铜质导电板和铁质导磁板组成,定子块由磁靴及永磁体组成,永磁体的布置采用相邻永磁体充磁方向相反的阵列方式。
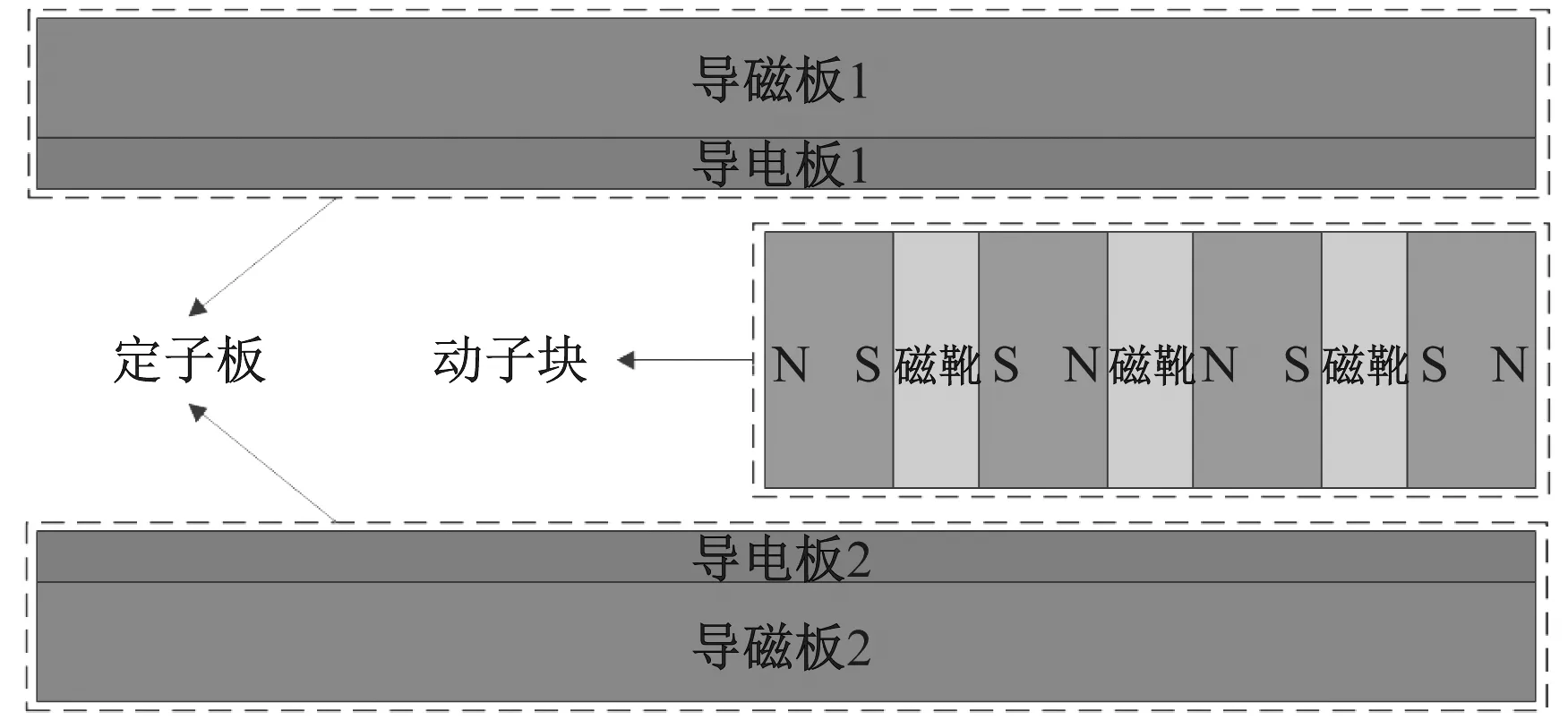
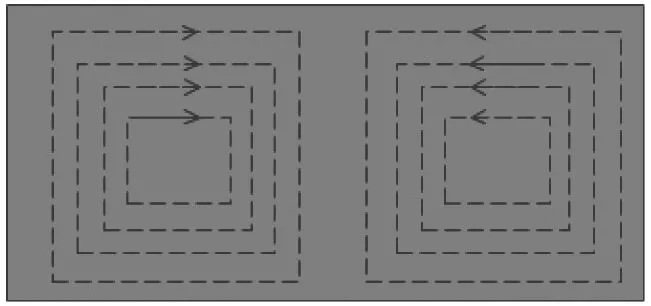
(a) 导电板上的涡流
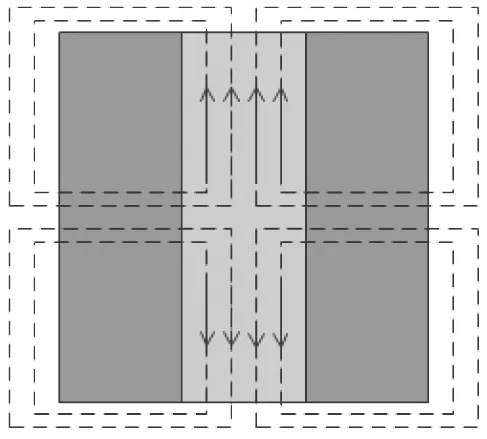
(b) 永磁体上的磁力线图1 平面式电涡流阻尼器物理模型Fig.1 Physical model of the planar eddy current damper
当动子块与定子板发生相对运动时,根据电磁感应原理,铜质导电板中会产生电涡流,进而激发出与动子块运动方向相反的作用力,阻碍动子与定子的相对运动。从能量的角度考虑,动子运动的机械能首先转化为铜质导电板的电能,并最终转化为阻尼热能进行耗散。影响平面式电涡流阻尼器磁阻尼特性的因素主要为磁场强度和涡流强度。尽管平面式电涡流阻尼器的相关理论研究已经取得了一定的进展[13],但其研究成果通常具有较强的针对性,本文采用电磁场有限元分析来研究高冲击载荷作用下的平面式电涡流阻尼器磁阻尼特性。
1.2 数值模型
本文选用Ansoft Maxwell电磁学有限元软件建立平面式电涡流阻尼器二维有限元模型如图2所示。在Model Depth中通过设置二维模型厚度,以模拟模型实际结构尺寸。并利用pwl函数输入发射载荷作用的高冲击载荷。该数值模型各部件的材料如表1所示。
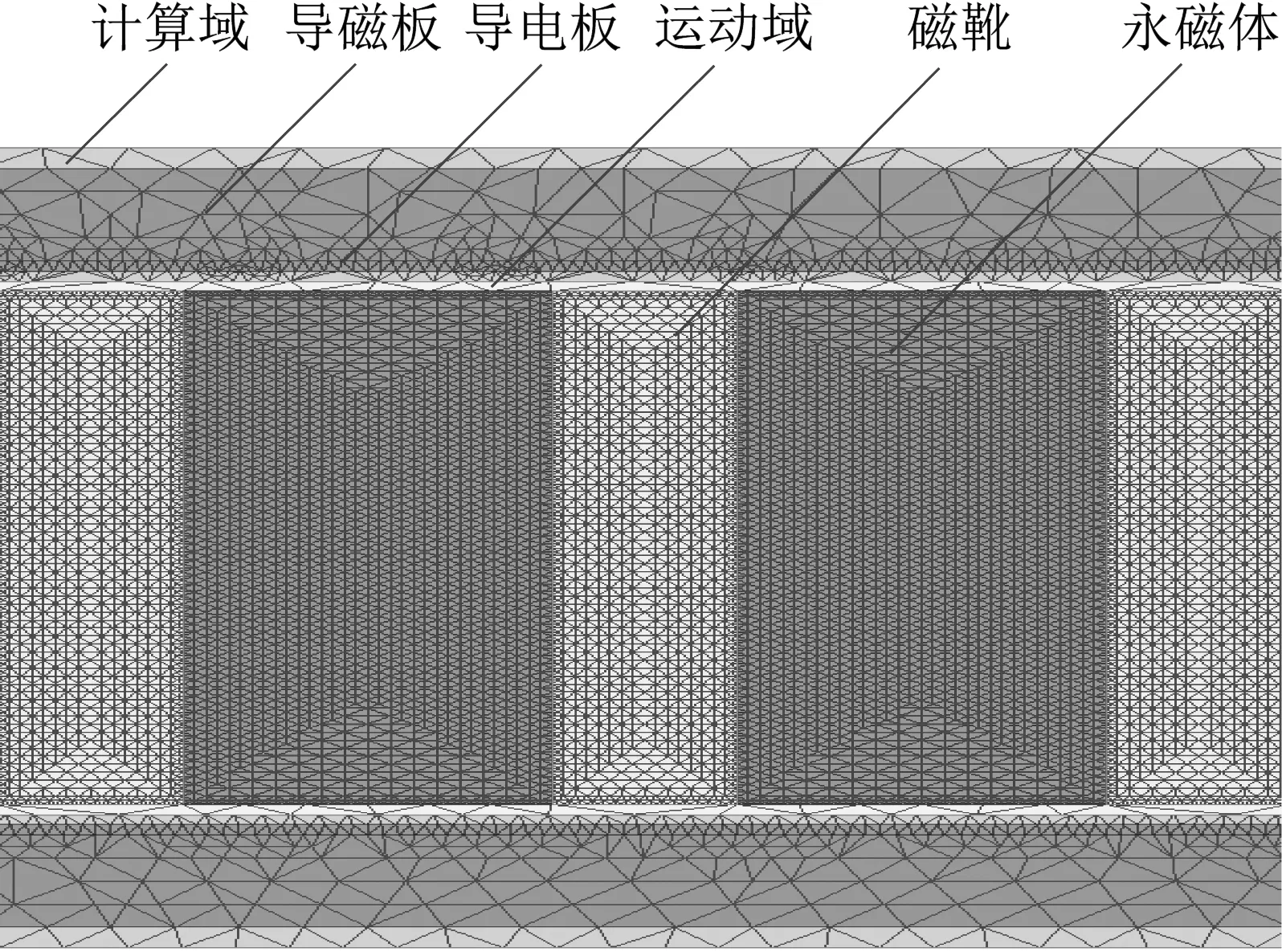
图2 平面式电涡流阻尼器二维局部网格模型Fig.2 Mesh model of the planar eddy current damper

表1 数值模型各部件材料Tab.1 Material of the numerical model parts
为进一步验证模型的准确性,通过不断的加密数值模型的网格数量提升网格质量,表2为7组数值模型的网格数量。通过对这7组不同网格质量的数值模型进行仿真计算,得到如图3所示的动子块速度曲线,可以发现,随着数值模型网格质量的不断提升,当网格数量超过376 462个时,动子块速度曲线逐渐趋于稳定。为节省计算时间,本文选择网格数量为631 586个的mesh-4网格剖分模式。
1.3 数值计算
图4为发射时产生的冲击载荷,图5为高冲击载荷作用下的平面式电涡流阻尼器动力学特性,可以看出,该平面式电涡流阻尼器能够满足安全制动某型火炮发射时产生的高冲击载荷。同时,平面式电涡流阻尼器的磁阻尼力在高速运行阶段出现了与文献[11]和文献[13]一致的阻尼削弱现象。这是因为随着动子块速度增大时,电涡流产生的感应磁场对永磁体主磁场的削弱作用增大和感应趋肤效应而引起的,由于本文研究平面式电涡流阻尼器在冲击环境中的应用,故需要对高速制动段的磁阻尼影响因素进行详细分析。
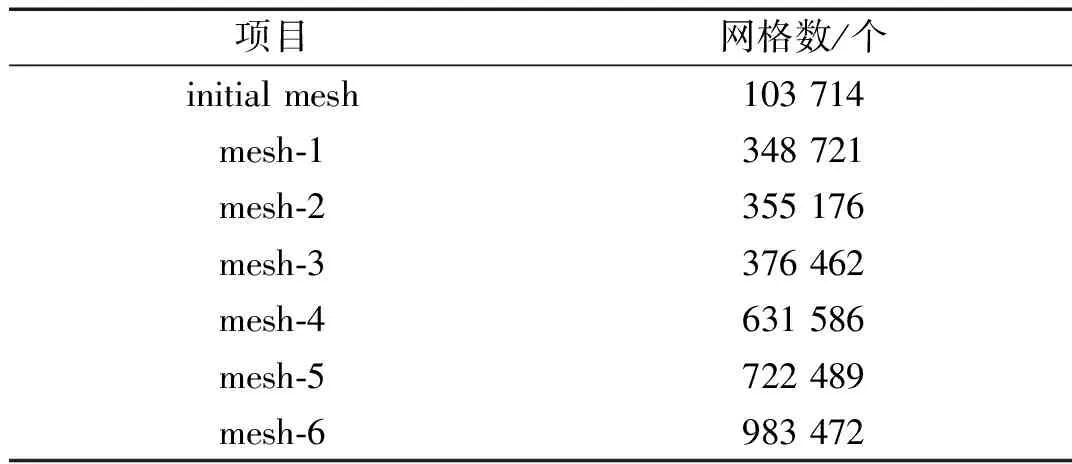
表2 数值模型网格数量
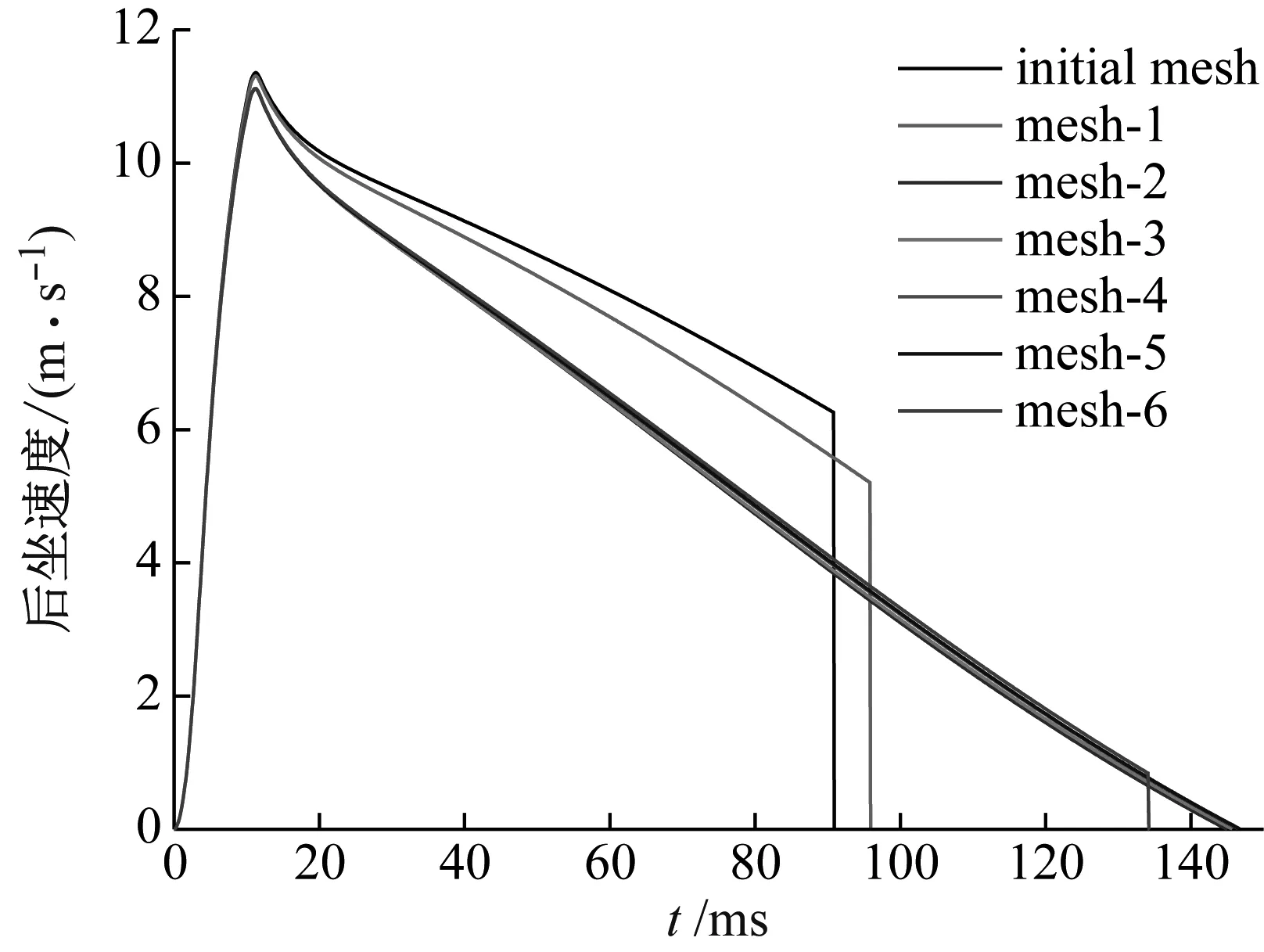
图3 不同网格质量的动子块速度曲线Fig.3 Speed curves of different mesh quality
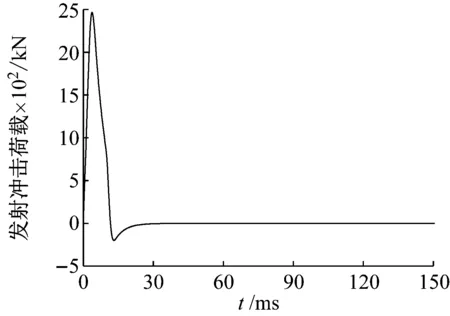
图4 发射时冲击载荷曲线Fig.4 Impact load curve during launch
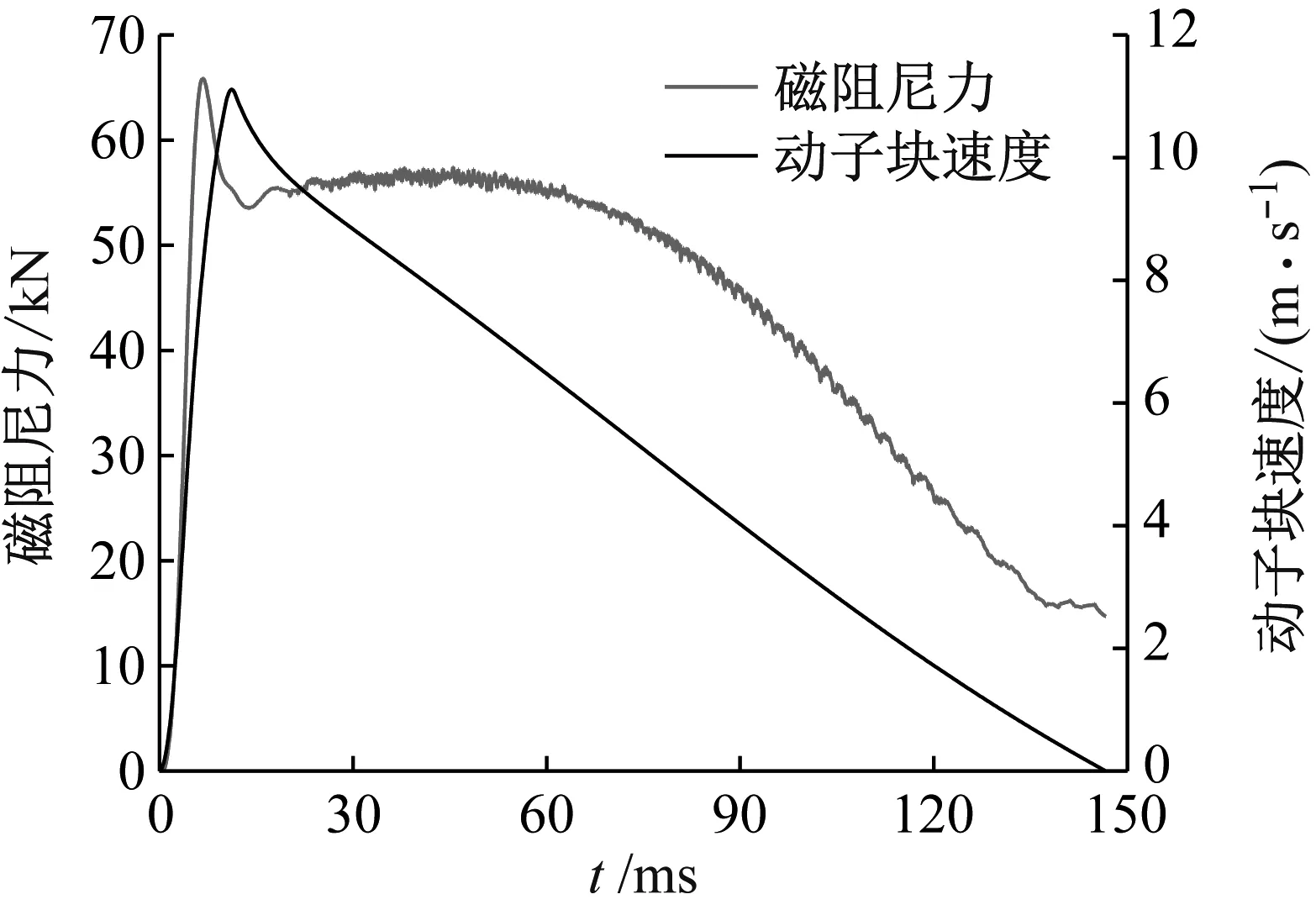
图5 冲击载荷作用平面电涡流阻尼器动力学特性
2 参数影响分析
2.1 永磁体结构尺寸
磁阻尼力受磁场强度的影响较大,而永磁体结构宽度和厚度对磁场强度有着直接的影响。平面式电涡流阻尼器结构尺寸参数如表3所示。

表3 平面式电涡流阻尼器结构参数
图6为不同永磁体宽度的磁阻尼曲线,随着永磁体宽度的增加,磁阻尼力随之增加,这是因为宽度的增加,增大了永磁体主磁场的磁场强度,但永磁体宽度的增加也增大了整个动子块的质量,为了量化表述动子块质量对磁阻尼力的影响,设定阻尼削弱后的磁阻尼稳定段均值与动子块质量之比为阻尼质量分配比
(1)
式中:Fsta为磁阻尼稳定段均值;m为动子块质量。
同时,随着永磁体宽度的增加,高速阶段的阻尼削弱现象越来越明显。在冲击载荷制动过程中,这种阻尼突然削弱的现象不利于制动的稳定性,为了量化表述阻尼削弱现象的大小,设定高速运行阶段阻尼凹陷处的磁阻尼力与磁阻尼峰值之比为峰值跌落比
(2)
式中:Fmax为磁阻尼峰值;Fval为凹陷处磁阻尼力。
如图7所示,随着永磁体宽度的增加,峰值跌落比和阻尼-质量分配比均呈现出下降趋势,这表明永磁体宽度增加虽然能够提高磁阻尼力,但是单位质量提供的磁阻尼力下降,永磁体的质量利用率降低。峰值跌落比也由88.5%下降为72.4%,峰值跌落更大。
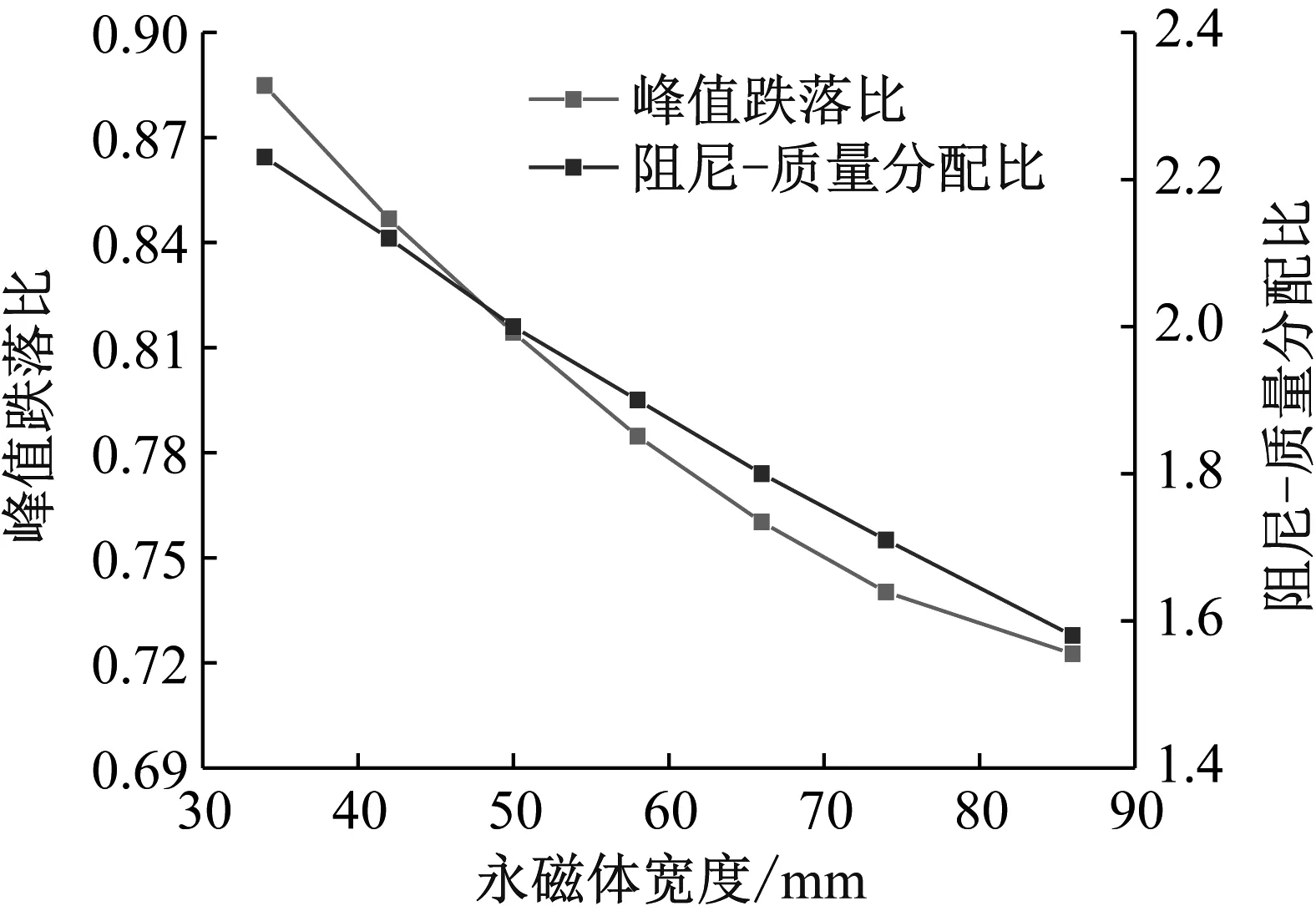
图7 不同永磁体宽度的磁阻尼特性Fig.7 Damping characteristics of different permanent magnet widths
图8为不同永磁体厚度的磁阻尼曲线,随着永磁体厚度的增加,磁阻尼力随之增加,这是因为厚度的增加,增大了永磁体磁动势。由图9可知,同一磁靴厚度条件下,不同永磁体厚度的磁阻尼峰值跌落比主要维在83.5%左右,同时存在先降低后增大的趋势,而阻尼-质量分配比则呈现出先增大后减小的趋势,在厚度为30 mm时达到最大。永磁体厚度增加不仅能够有效提高磁阻尼力,对峰值削弱现象的影响也较为平稳。在质量增加相同情况下,相比于增大宽度,增大永磁体厚度更为有利。
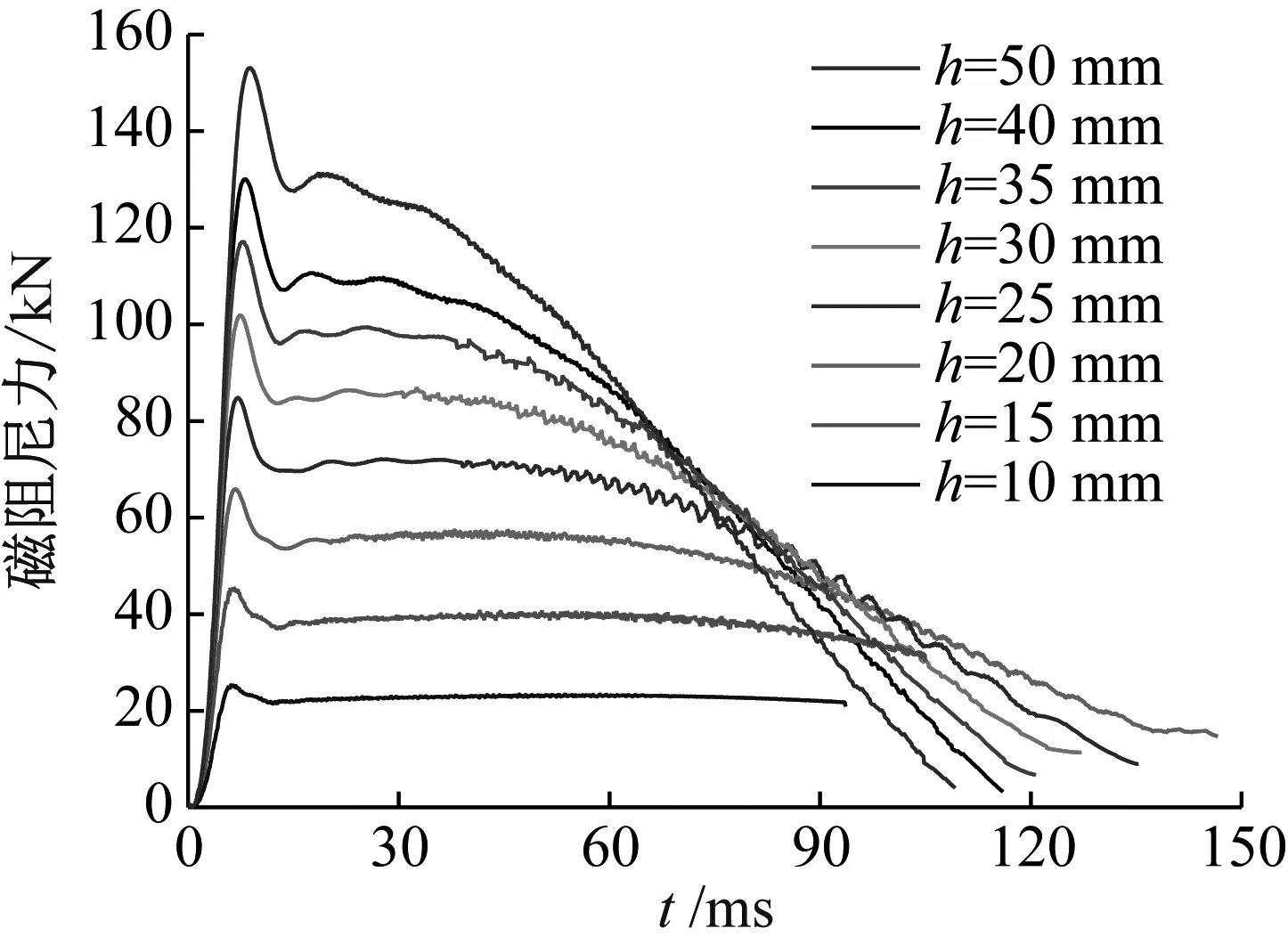
图8 不同永磁体厚度的磁阻尼曲线Fig.8 Damping curves for different permanent magnet thickness
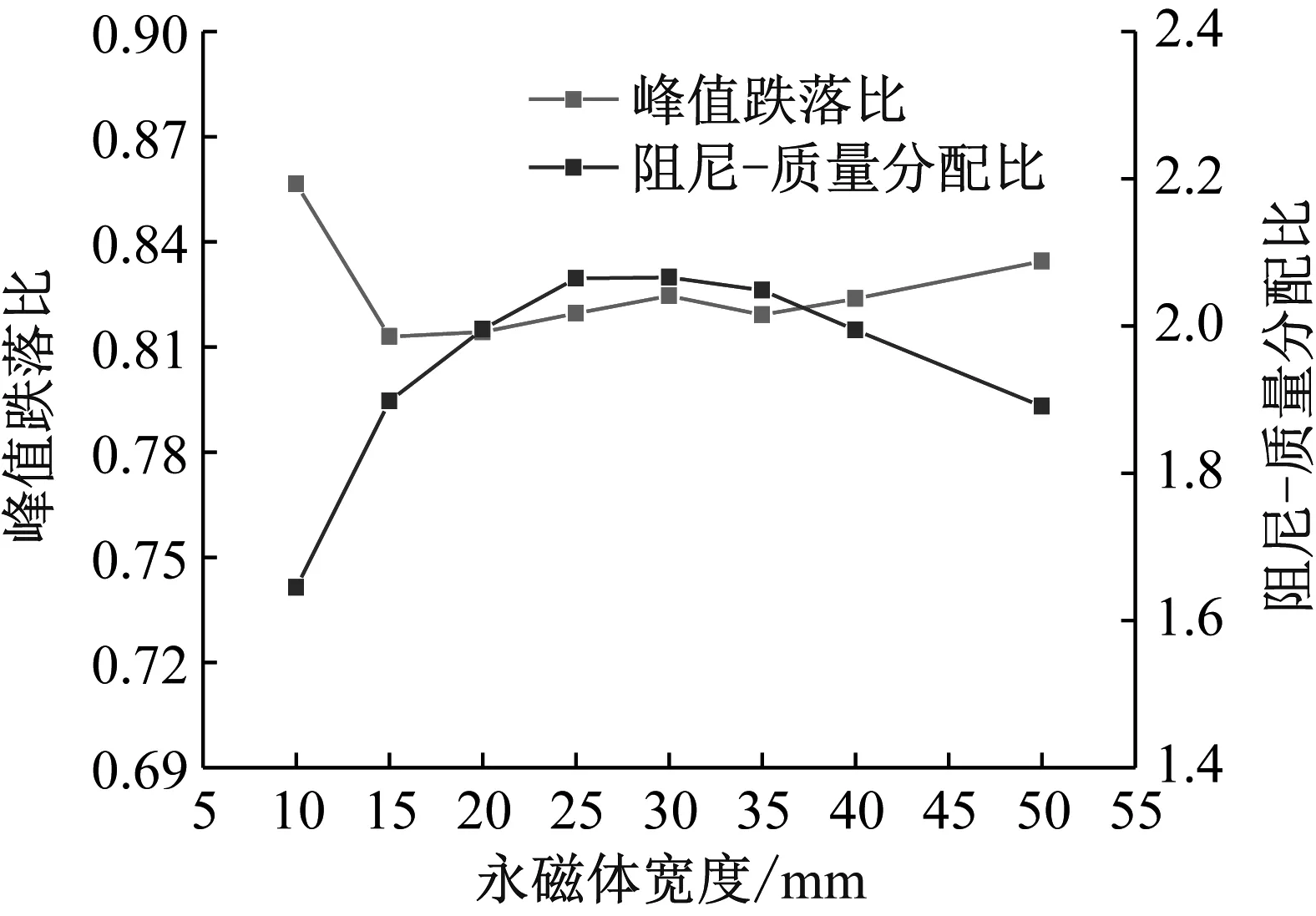
图9 不同永磁体厚度的磁阻尼特性Fig.9 Damping characteristics of different permanent magnet thickness
2.2 磁靴结构尺寸
图10为不同磁靴厚度的磁阻尼曲线,可以看出,随着磁靴厚度在一定范围内增加,磁阻尼力峰值跌落后的平稳段幅值变化不大。这是由于在永磁体结构尺寸一定时,磁场强度确定,磁靴导磁性能趋于饱和,磁靴厚度从6 mm增大到14 mm时对导磁性能影响不大,而当磁靴厚度增大到26 mm时,磁靴导磁性能不饱和时,磁阻尼力开始出现较为明显的波动变化。图11为不同磁靴厚度的磁力线分布,磁极相对的相邻永磁体磁力线同时导入磁靴当中,并相互排斥,从磁靴两端导出进入气隙,当磁靴厚度较大时,相邻永磁体的磁力线斥力减小,使得垂直进入气隙的磁力线减小,磁阻尼力下降。
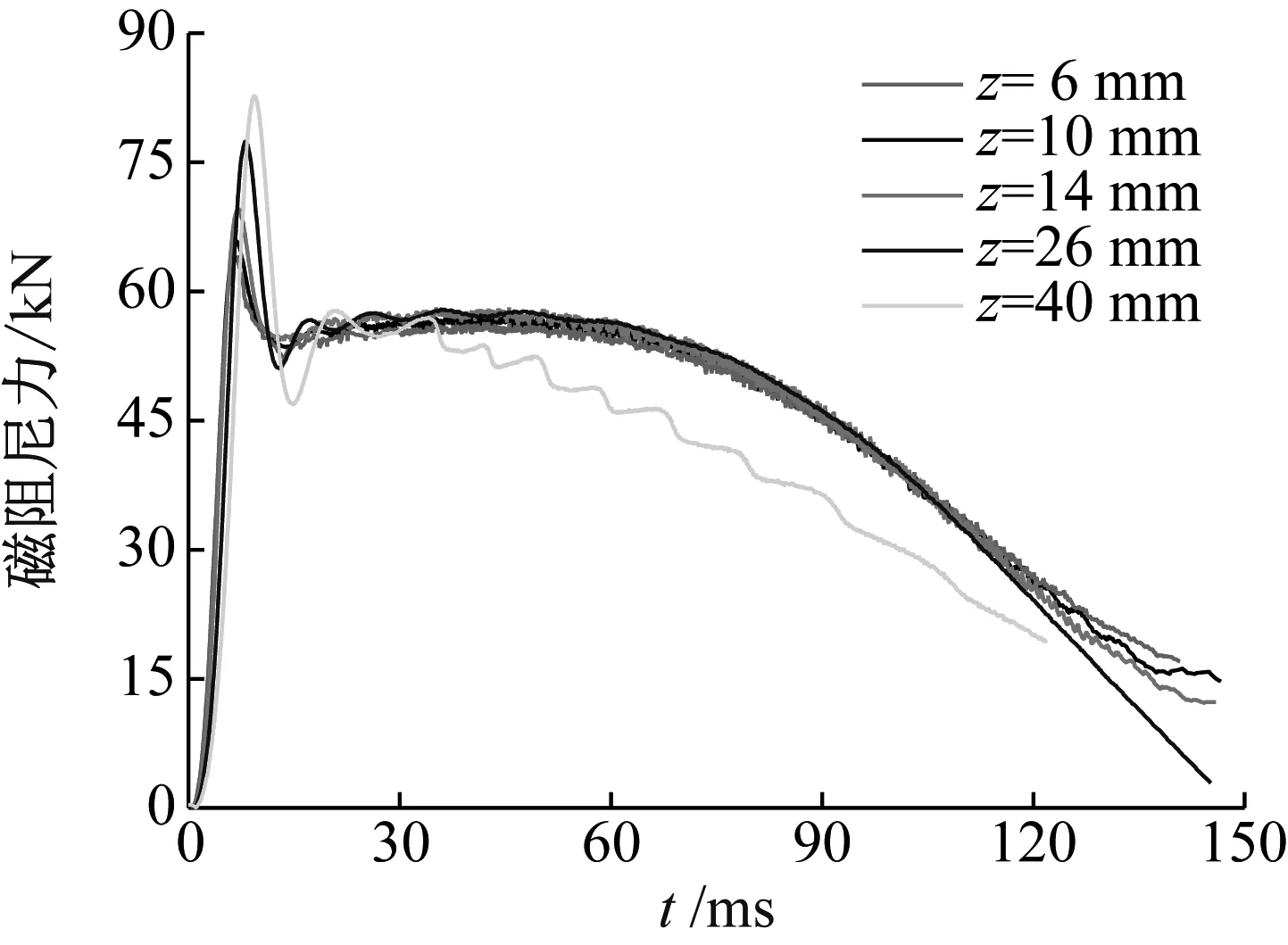
图10 不同磁靴厚度的磁阻尼曲线Fig.10 Damping curves of different magnetic boots thickness
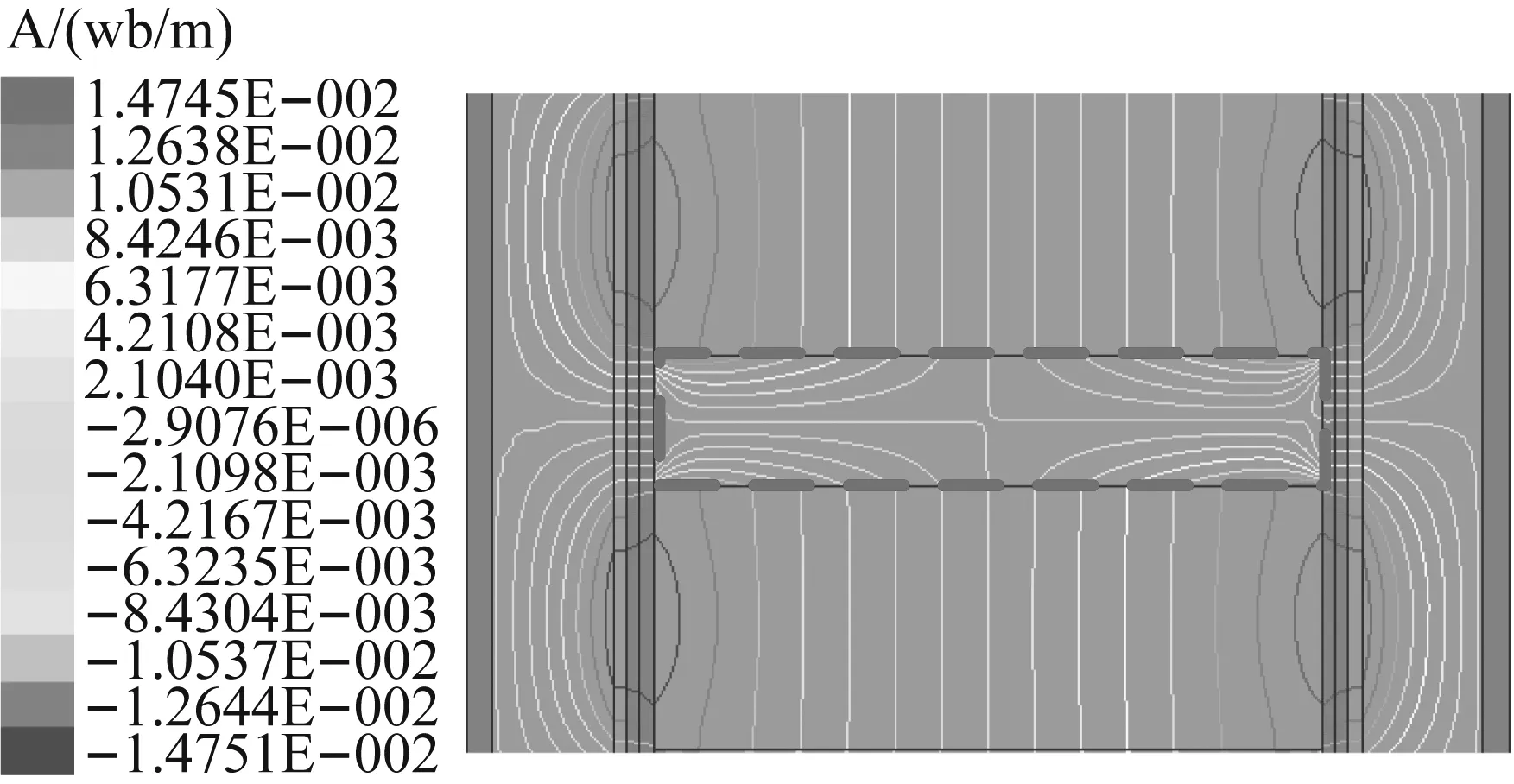
(a) 磁靴厚度z=10 mm
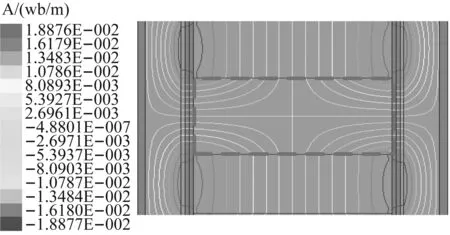
(b) 磁靴厚度z=36 mm图11 不同磁靴厚度的磁力线分布Fig.11 Magnetic field distribution of different magnetic boots thickness
2.3 导磁板厚度
图12为不同导磁板厚度的磁阻尼力曲线,有无导磁板的磁阻尼力相差较大,而导磁板的厚度变化对磁阻尼力的影响不大,在导磁板厚度超过2 mm后,磁阻尼力即趋于稳定。这是因为铁质导磁板为软磁性材料,其最大磁导率较高,磁阻较小,使得磁力线向铜质导电板的外侧汇聚,极大增加了铜质导电板的磁感应强度。而当导磁板厚度超过一定值后,导磁板对永磁体的主磁场的导磁效果开始趋于饱和,导磁板厚度影响趋于稳定。
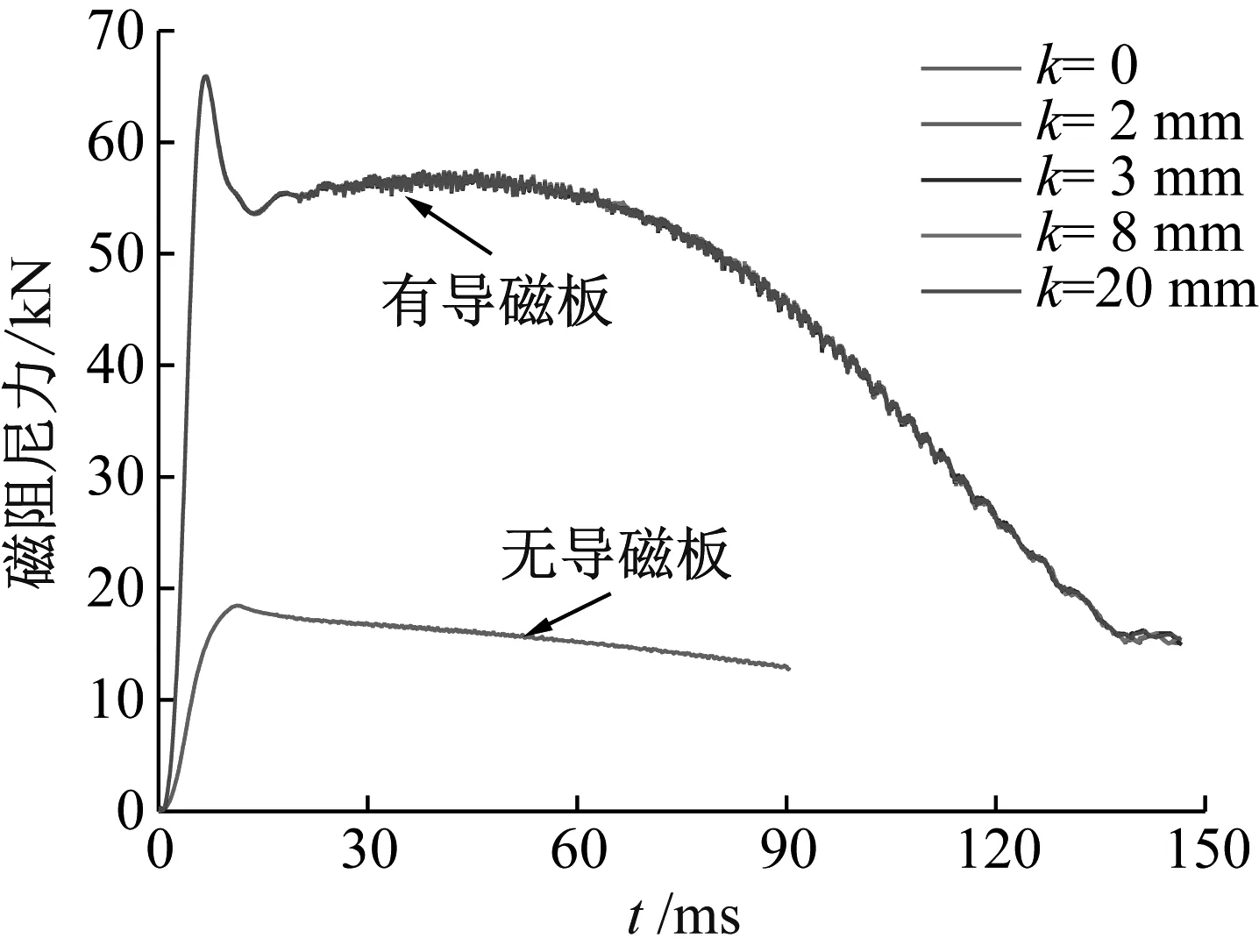
图12 不同导磁板厚度的磁阻尼曲线Fig.12 Damping curves of different permeable plate thickness
图13为不同导磁板厚度的铜质导电板上的x方向和y方向的磁通量,其中,x方向为垂直于导电板方向,y方向平行于导电板方向。由电磁感应原理可知,磁阻尼力主要与垂直于导电板方向的磁通量有关。从图12可以看出,无导磁板时x方向的磁通量小于有导磁板时x方向的磁通量,导磁板厚度超过2 mm后x方向的磁通量快速升高,并逐渐趋于稳定。同时y方向的磁通量快速降低,也趋于稳定。
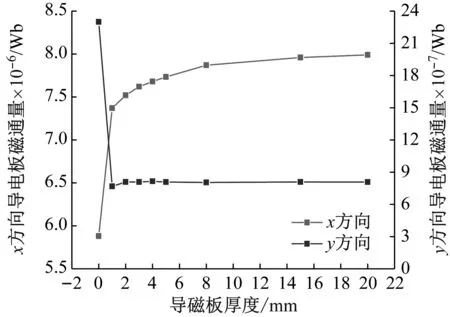
图13 不同导磁板厚度的导电板磁通量
2.4 导电板厚度
图14为不同导电板厚度的磁阻尼曲线,当导电板厚度从0增加到0.6 mm时,磁阻尼力逐渐呈比例增大,这是因为在这一阶段导电板厚度的增加,使得涡流区的厚度增加,涡流强度增加引起了磁阻尼力的呈比例增大。当导电板厚度从0.8 mm增加到2.0 mm时,磁阻尼力的阻尼削弱现在逐渐明显,峰值跌落比明显增大,这是因为随着涡流强度的继续增加,涡流产生的感应磁场对永磁体主磁场的削弱作用也随之增大。图15为1.0 mm厚度的导电板在不同时刻的磁感应强度,在动子块加速阶段,导电板的磁感应强度开始增大,在6.5 ms速度最大点时,导电板的磁感应强度达到最大,引起这一时刻以后的阻尼力开始削弱,直至14 ms磁阻尼跌落点时,导电板的磁感应强度减小,磁阻尼力开始回升,在动子块减速阶段,导电板磁感应强度逐渐平稳。
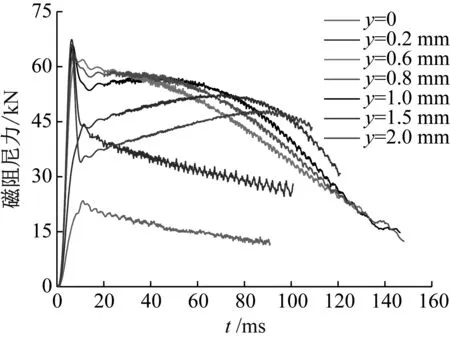
图14 不同导电板厚度的磁阻尼曲线Fig.14 Damping curves of different conductive plate thickness
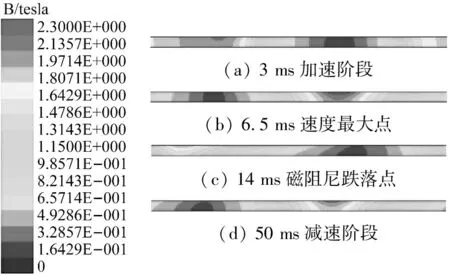
图15 不同时刻导电板磁感应强度
2.5 气隙间距
图16为不同气隙宽度的磁阻尼曲线,可以明显看出,随着气隙间距的增大,磁阻尼力减小,气隙间距微小的变化,也对磁阻尼力造成较大影响,并且气隙间距还与阻尼器各部件的加工工艺、工装误差等因素密切相关,需要在设计时综合考虑。相关试验研究也认为,为了提高电涡流阻尼器工作效率,在保证所需安全条件时,应当尽可能的减小气隙间距。
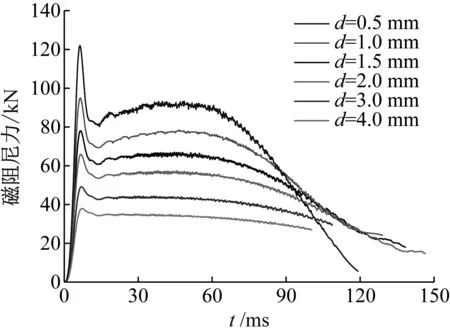
图16 不同气隙宽度的磁阻尼曲线Fig.16 Damping curves of different air gap widths
3 结 论
本文通过对高冲击载荷作用平面式电涡流阻尼器特性进行数值模拟研究,分析了永磁体和磁靴结构尺寸、导电层和导磁层厚度以及气隙间距对电磁阻尼力的影响,得出以下结论:
(1) 平面式电涡流阻尼器能够满足安全制动某型发射时产生的高冲击载荷,在高速阶段会出现阻尼削弱现象。在相同发射载荷下,平面式电涡流阻尼器结构参数较小。
(2) 与增加永磁体宽度相比,增加永磁体厚度能够有效提高磁阻尼力,且当永磁体厚度为30 mm时其质量利用率将达到最大。
(3) 磁靴厚度和导磁板厚度由于导磁性能饱和的影响,使得磁靴厚度在10 mm时性能最优,而导磁板厚度超过2 mm后磁阻尼力开始趋于饱和。
(4) 由于涡流产生的感应磁场对永磁体主磁场的削弱作用,导电板厚度从0增加到0.6 mm时,磁阻尼力成比例增大,但当导体板厚度由0.8 mm增加到2 mm时,高速阶段的磁阻尼削弱现象明显增大。
(5) 磁阻尼力受气隙间距的影响单一,但敏感程度较大,为了提高电涡流阻尼器工作效率,在保证所需安全条件时,应当尽可能的减小气隙间距。
