考虑扣件温频变的车轨桥垂向耦合系统振动能量研究

刘林芽， 李 辉， 秦佳良， 左志远， 孟宪金

(华东交通大学 铁路环境振动与噪声教育部工程研究中心， 南昌 330013)

随着时代的发展，列车行驶速度不断提高，在给生活带来便利的同时，也给线路养护部门带来了各种养护难题。当列车在运行时，轮轨之间的相互接触会引起巨大振动，这个振动会通过扣件向下传递至轨道及其下部支撑结构上，但实际运营中有时会因为轨道结构中的振动能量过大，远超结构和部件的能量承受极限，导致轨道结构及部件伤损。国内外学者已将功率流[1-2]作为一种更完善的振动能量评价标准应用于轨道振动研究中。Jiang等[3]基于功率流理论建立了高速铁路车辆-轨道-桥梁计算模型对轨道-桥梁系统的振动能量特性进行了评价，并分析了滑动层面刚度、扣件刚度等参数对轨-桥耦合系统振动能量的影响。谷爱军等[4]通过将基础结构部分简化为简支梁建立了单块浮置板轨道振动能量传递计算模型，根据功率流理论分析了浮置板和基础梁的结构参数对输入至基础结构的振动能量的影响。顾民杰等[5]基于功率流计算理论计算了轮轨滚动激励引起的轨道和桥梁空间的平均振动均方速度，并对比分析了U型梁与双箱双室梁及单箱单室梁之间的振动差异。李增光等[6]建立车-轨-桥耦合系统振动模型，采用功率流法研究了耦合系统中不同轨道结构子系统的振动能量特性，并探讨了垫片阻尼、扣件刚度等参数对输入至高架桥的振动能量的影响。Li等[7]提出了基于力法原理的车轨桥系统功率流分析方法，分析了轨道交通槽型梁的振动与噪声的主导频率。付娜等[8]通过功率流法分析与评价了设置减振垫对于桥上双块式无砟轨道振动能量特性的影响，并探讨了设置减振垫引起的轨道结构能量重分布问题。但是在上述研究中，车辆-轨道-桥梁耦合系统中钢轨扣件动参数都取的是定值，但是实际运营中钢轨扣件动参数会受到环境温度和激振频率等因素的影响，这是由于扣件系统中主要提供弹性和阻尼性能的组成部分是扣件弹性垫板，扣件弹性垫板中含有橡胶高分子材料，这种高分子材料的动态力学特性与激振频率和环境温度等因素有关[9]。钢轨扣件作为高速铁路不可或缺的组成部分，其作用是弹性地吸收轮轨作用力并将轮轨接触产生的振动能量传递至轨下基础，扣件的力学性能会对车辆-轨道垂向动力响应造成很大影响[10]，而动力响应的改变会对结构振动能量产生巨大影响。因此忽略扣件的温频变动态力学特性会导致难以精准预测轨道结构振动能量分布特性。

综上所述，本文将通过动态力学分析仪对扣件进行定频变温试验，获取扣件弹性垫板的模量及损耗因子随温度变化的关系，结合温频等效原理与高阶分数导数FVMP模型[11]建立能充分表征扣件的温频变动态力学特性的扣件模型，并将其嵌入车辆-轨道-桥梁垂向耦合系统模型中。基于功率流法系统地研究扣件温频变特性对车辆-轨道-桥梁垂向耦合系统的振动能量分布及传递的影响。

1 扣件温频变力学性能试验及模型拟合

1.1 扣件温频变力学性能试验

由于扣件的主要力学性能由扣件弹性垫板体现，故本文以高速铁路常用的常阻尼弹性垫板为试验对象，如图1～图3所示。扣件弹性垫板主要物理和力学指标如表1所示。通过德国GABO公司生产的动态力学分析仪的压缩模式对弹性垫板进行温度扫描试验，获取扣件弹性垫板的模量和损耗因子随温度的变化曲线。试验时设置设备的固定试验频率为 2 Hz，设置动态应变为0.1 %，温度设置在-60～40 ℃，扣件胶垫试件尺寸选用直径15 mm,厚度10 mm的圆柱体作为试验试件，对于弹性垫层分别制作三组试件，进行平行试验。给弹性垫层试样施加预荷载后，进行温度扫描试验，试验设置仪器的升温速率为2 ℃/min，台阶升温中，每个台阶高度为2 ℃，恒温时间300 s，测定试样的荷载-位移响应随温度的变化，最终获取弹性垫层动参数的温度谱。

图1 扣件整体构造示意图Fig.1 Overall structure of fastener

图2 试验样本Fig.2 Test sample

图3 动态力学分析仪Fig.3 Dynamic thermomechanical analysis

表1 弹性垫板性能参数Tab.1 Performance parameters of elastic base plate

图4为-60 ℃～40 ℃温度范围内扣件弹性垫板的模量与损耗因子随温度变化的曲线，在低于-50 ℃的温度范围内，弹性垫板的储能模量随温度升高而小幅下降，而在温度低于-46 ℃时耗能模量数值则随温度的升高而上升，并在-46 ℃左右达到峰值；当温度在-46 ℃及以下时弹性垫板处于玻璃态，此时弹性垫板的储能模量值较大，并具有刚硬性；而随着温度的不断升高当超过弹性垫板玻璃态极限温度后，弹性垫板模量值会陡然降低，且降速逐渐趋于缓和。扣件弹性垫板的损耗因子-46 ℃左右存在明显的峰值，当温度大于-46 ℃时，损耗因子逐渐减小且降速渐渐变缓，而当温度继续升高至0 ℃以后，损耗因子的变化变得非常缓和。

(a) 模量值

(b) 损耗因子图4 常阻尼扣件弹性垫板Fig.4 Constant damping fastener elastic pad

1.2 扣件温频变的FVMP模型参数识别

FVMP模型是一种高阶分数导数模型，其能准确描述扣件弹性垫板在较宽频率范围内的动态力学特性，为了能够准确描述温度与频率对扣件弹性垫板动态力学特性的影响，本文将温频等效原理与FVMP模型相结合，建立一种考虑了温频变特性的FVMP模型。FVMP模型频域本构方程参考文献[11]。

根据温频等效原理[12]，密度为ρ的黏弹性材料，在激振频率为ω、温度为T的条件下，其复模量Y*(ω,T)在进行公式换算后可转换为温度T0、密度ρ0及ωα(T)频率条件下的复模量Y*[ωα(T),T0]，其表达式

(1)

式中，α(T)为温度转换因子，其可对不同温度或不同频率下的橡胶黏弹性材料的力学特性进行转换。

α(T)可用WLF方程表示

(2)

式中：C1与C2为常数；T0与温度和弹性垫板黏弹性材料的种类有关。

将式(2)代入式(1)，并分离实部与虚部通过计算即可得到包含温度和频率因子的温频变动态力学模型表达式

(3)

(4)

(5)

图5为温频变动态力学模型预测的模量值与损耗因子。由图5可知，钢轨扣件弹性垫板的黏弹性力学特性随频率和温度的变化关系是非线性的。温度越低，荷载频率越高，弹性垫板的模量值越大，例如温度-40 ℃、频率1 000 Hz条件下常阻尼弹性垫板的储能模量增大至1 960 MPa，说明弹性垫板在低温高频条件下具有刚硬的特性，而1 Hz、20 ℃下的预测值仅为15 MPa，且在20～40 ℃的低频条件下，弹性垫板的模量值相差较小，这也证实了弹性垫板在高温低频条件下具有柔软的特性。弹性垫板的损耗因子随着频率的升高而增大，在低温高频条件下的数值大于1，此时弹性垫板的耗能刚度大于储能刚度；当温度从-40 ℃逐渐升高至40 ℃时，弹性垫板的损耗因子减小，且降速逐渐变缓。由此可以看出，所建立的温频变动态力学模型能够准确地描述弹性垫板的黏弹性力学特性。

(a) 储能模量

(b) 耗能模量

(c) 损耗因子图5 弹性垫板温频变动态力学模型表征Fig.5 Characterization of dynamic mechanical model of temperature-frequency change of elastic pad

2 考虑扣件温频变的车-轨-桥耦合振动功率流计算模型

由上述可知，扣件的动参数与环境温度和激振频率有关。因此，在车-轨-桥耦合振动模型中加入扣件温频变动态力学模型分析其对轨道结构振动能量的影响显得尤为必要。现以中国CRH380A型高速客车与CRTSII型板式无砟轨道为例，分析扣件温频变动态特性对车-轨-桥耦合振动能量的影响。

2.1 计算模型

建立图6所示的车-轨-桥垂向耦合振动模型，采用功率流法分析与评价扣件温频变动态力学特性对车轨桥耦合系统振动能量的影响。模型中的扣件采用新建的考虑温频变的FVMP模型代替传统的线性模型。

图6 计算模型Fig.6 Calculation model

车辆系统采用10个自由度的半车模型，其分别为4个车轮的垂向位移zw1、zw2、zw3、zw4，2个转向架的点头θt1、θt2和浮沉zt1、zt2，车体的点头θc、浮沉zc。车辆系统振动微分方程为

(6)

式中：Cv、Mv、Kv分别为车辆系统的阻尼、质量、刚度矩阵；Pv为车辆系统上作用的外力；Zv为车辆系统的位移矢量。

由谐波不平顺引起的垂向轮轨力为谐荷载，在谐荷载作用下车辆做简谐振动，因此设式(6)中P(t)、zV(t)分别等于频域范围内不平顺引起的垂向轮轨力的幅值P(ω)eiwt和车辆系统的位移幅值ZV(ω)eiwt，并将其代入式(6)即可求出车辆系统的稳态响应为

(7)

在通过动柔度理论，可求得车轮动柔度为

(8)

由于钢轨存在剪切变形，故钢轨采用无限长的Timoshenko梁模拟，其振动方程为

(9)

(10)

式中：ω为激振圆频率；zr为钢轨垂向位移；Er为杨氏模量；Ir为截面惯性矩；κ为剪切系数；ηr为损耗因子；Ar为横截面面积；Gr为剪切模量；φr为截面转角；ρr为钢轨密度。

设βr(x1,x2)为动柔度函数，表示单位力在钢轨x1处作用时x2处的位移。通过式(9)、式(10)与动柔度函数定义相结合，得到Timoshenko梁钢轨动柔度表达式为

βr(x1,x2)=u1e-ik1|x1-x2|+u2e-k2|x1-x2|

(11)

由轮轨耦合振动响应叠加原理可得钢轨在频域内的振动位移为

(12)

式中：Nw为轮对数；xw为第w个轮轨接触点的位置；Kfzr(xn)为第n个扣件作用在钢轨xn处的扣件反力；Pw为第w个轮轨接触点上的轮轨力；N为扣件数。

Kf为扣件弹性垫板的复刚度，其表达式为

(13)

式中：h、A为扣件弹性垫板的厚度与横截面面积；Ys为扣件弹性垫板的储能模量；δ为弹性垫板的损耗因子。Ys、δ的大小与激振频率和环境温度有关。

轨道板简化为两端自由的Euler-Bernoulli梁，轨道板频域内的振动位移表达式为

(14)

式中：βs(x1,xn)为轨道板动柔度函数，N为所有扣件的个数，Ffn为第n个扣件力；Fjm为CA砂浆层第m个离散弹簧力；M为CA砂浆层离散弹簧个数。

桥梁简化为简支Euler梁，其频域内振动位移表达式为

(15)

式中，Fzh为第h个桥梁支座施加到桥梁xzh处的支反力。

通过联立式(10)、(12)、(13)可得矩形矩阵

[βK]{Z}={P}

(16)

式中：[βK]为由轨道-桥梁各结构动柔度乘复刚度组成；{Z}为由轨道-桥梁各结构位移组成；{P}为荷载矩阵。

由式(16)可以求出轨道桥梁的动柔度为

(17)

轨桥动柔度与车轮动柔度一样可写为

(18)

轮轨接触弹簧动柔度的计算根据文献[13]可得

(19)

式中：I4×4是4×4的单位矩阵；I4×4βC为轮轨接触弹簧的动柔度矩阵；kc称为线性化的轮轨接触刚度系数。

通过虚拟激励法[14]求解车-轨-桥系统随机振动响应，其中Srr(ω)为轨道不平顺谱密度，由于列车行驶时4个轮轨接触点之间存在位移差，因此对应的虚拟激励可表示为

R(ω)=

(20)

通过上述所建立的车-轨耦合模型可得轮轨动态作用力Pwr表达式

Pwr=-(βV+βRB+I4×4βC)-1R(ω)

(21)

式中：βV为车轮动柔度矩阵，βRB为轨道桥梁动柔度矩阵；I4×4是4×4的单位矩阵，I4×4βC为轮轨接触弹簧的动柔度矩阵。

将式(6)、式(16)结合，求出车辆、轨道、桥梁各结构位移响应，在通过位移响应求出结构振动响应。

2.2 输入功率流计算

轨道结构的功率流又名平均功率流，其根据计算方法的不同分为时域、频域两种。而本文分析的是频域范围内扣件温频变特性对车轨桥耦合系统振动能量的影响，因此使用频域平均功率来分析振动能量在车轨桥耦合系统中的传递。

通过频域车辆-轨道-桥梁耦合动力学模型计算得到各个离散阻尼弹簧的力Fi(k)和各个节点的速度Vi(k)，再对各个节点的速度Vi(k)取共轭后与Fi(k)相乘，得到的结果取其实部就是所求的结构节点功率流[15]，表达式为

(22)

由于式(22)是对结构某特定节点的功率流进行计算，其并不能反映整个结构的振动能量，故需要进行多节点功率流求和得到结构输入总功率流，求和公式为

(23)

式中：i为功率流的节点序号；n为节点总数；k为计算点频率。

在得到轨道-桥梁系统的总功率流后，为了方便比较，还需要将其转换为相对功率流，转换公式为

(24)

式中：Pω(k)为频率k对应的结构总功率流；P0为基准功率流取1×10-8N·m/s；Pre(k)为频率对应的结构相对功率流，dB。

本文采用CRH380A型高速列车车辆及CRTSII板式无砟轨道，结构的计算参数参考文献[10]。本文将通过四种工况来综合描述扣件温频变特性对系统振动能量的影响，工况分类如表3所示，其中24 ℃定值工况下扣件刚度取2.7×104kN/m，损耗因子取0.25，扣件温频变特性下的动参数由新建的模型给出。

表3 计算工况

3 结果分析

以常用的短波不平顺谱Sato谱(波长为1 m以下)作为高频激励，以德国高速轨道谱(波长为1～100 m)作为低频激励，行车速度设为350 km/h，采用上述模型计算车辆与轨道系统在不同工况下的振动能量特性。

3.1 轨道结构振动能量分布研究

图7所示为不同工况下的钢轨振动能量的分布，从图中可以看出，钢轨振动能量曲线的第一主频为52～207 Hz内的中频，其与车轮和轨道的耦合振动有关。不同工况下钢轨振动能量在整个频段内都有所不同，这是由于考虑扣件的温频变特性后轨道结构参数发生了改变。不同工况下在6 Hz处都有一个峰值，这是因为该频域为桥梁一阶共振频域。24 ℃常温下考虑扣件频变特性后钢轨振动能量在中频段内的峰值增加了11.3 dB，其对应的峰值频率也向右偏移至59 Hz左右。-40 ℃频变工况与24 ℃频变工况相比，钢轨振动能量的峰值增加了4.1 dB，其对应的峰值频率也向右偏移至206 Hz左右，这是由于温度的降低使得扣件的刚度增大，轮轨力也随之增大，因此钢轨功率流会增大。

图8和图9为不同工况下轨道板与桥梁振动能量的分布，从图中可以发现，不同工况下的轨道板振动能量的变化趋势与桥梁振动能量大致相似，在29 Hz以内的低频段无明显变化，而在中高频段内振动能量随温度的降低而增大，24 ℃常温下考虑扣件频变特性后轨道板与桥梁振动能量在中频段内的峰值分别增加了2.5 dB、3.8 dB，其峰值频率也向右偏移至55 Hz处。-40 ℃低温条件与24 ℃常温相比，轨道板与桥梁振动能量在87 Hz后振动能量开始增大，轨道板与桥梁振动能量峰值分别增加了4 dB、5.5 dB，其峰值频率也向右偏移至203 Hz处左右。这是由于温度的降低使得扣件的刚度增大，扣件下部结构振动响应会变大，因此其由上至下传递的振动能量也会变大。

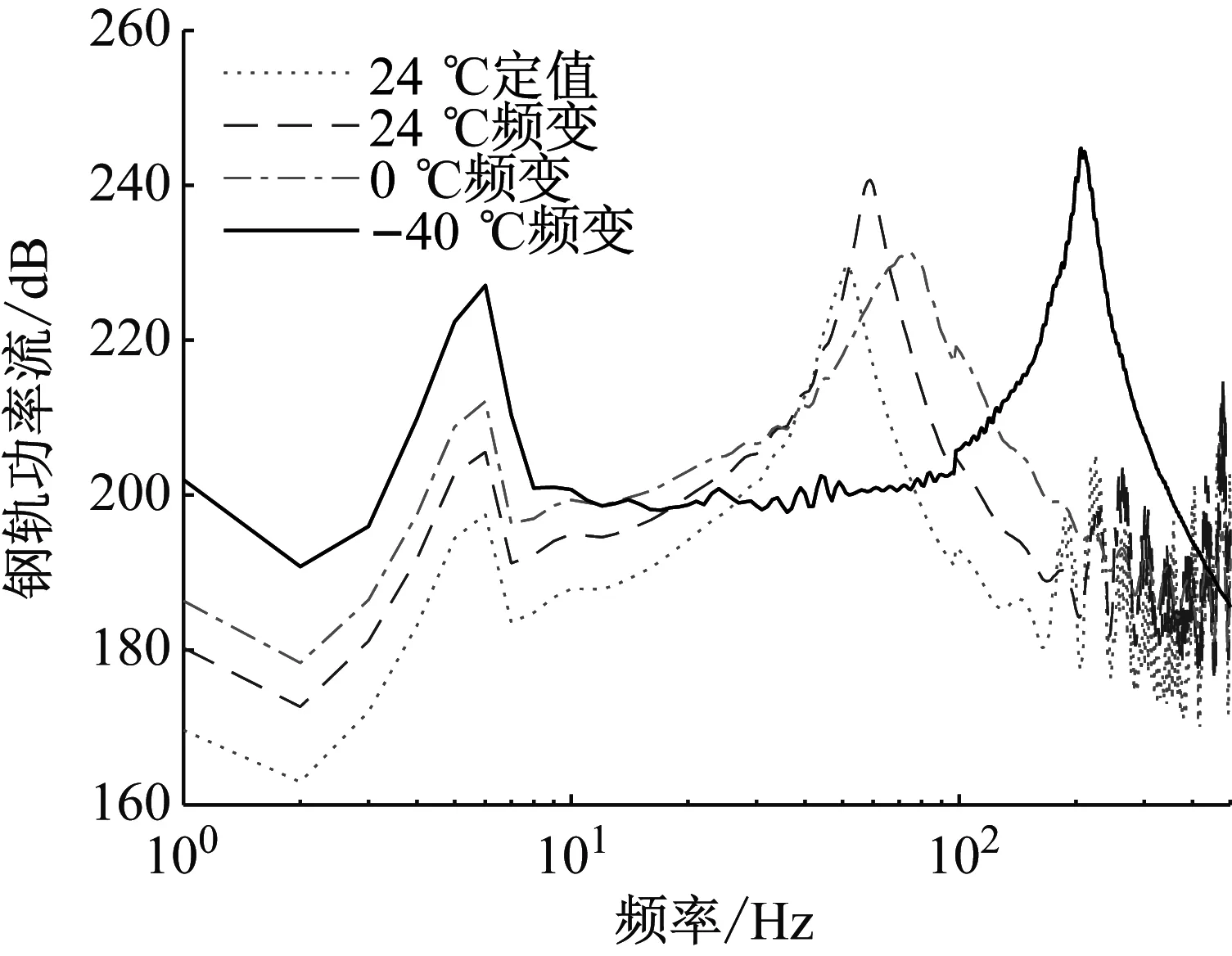
图7 钢轨振动能量图Fig.7 Rail vibration energy diagram

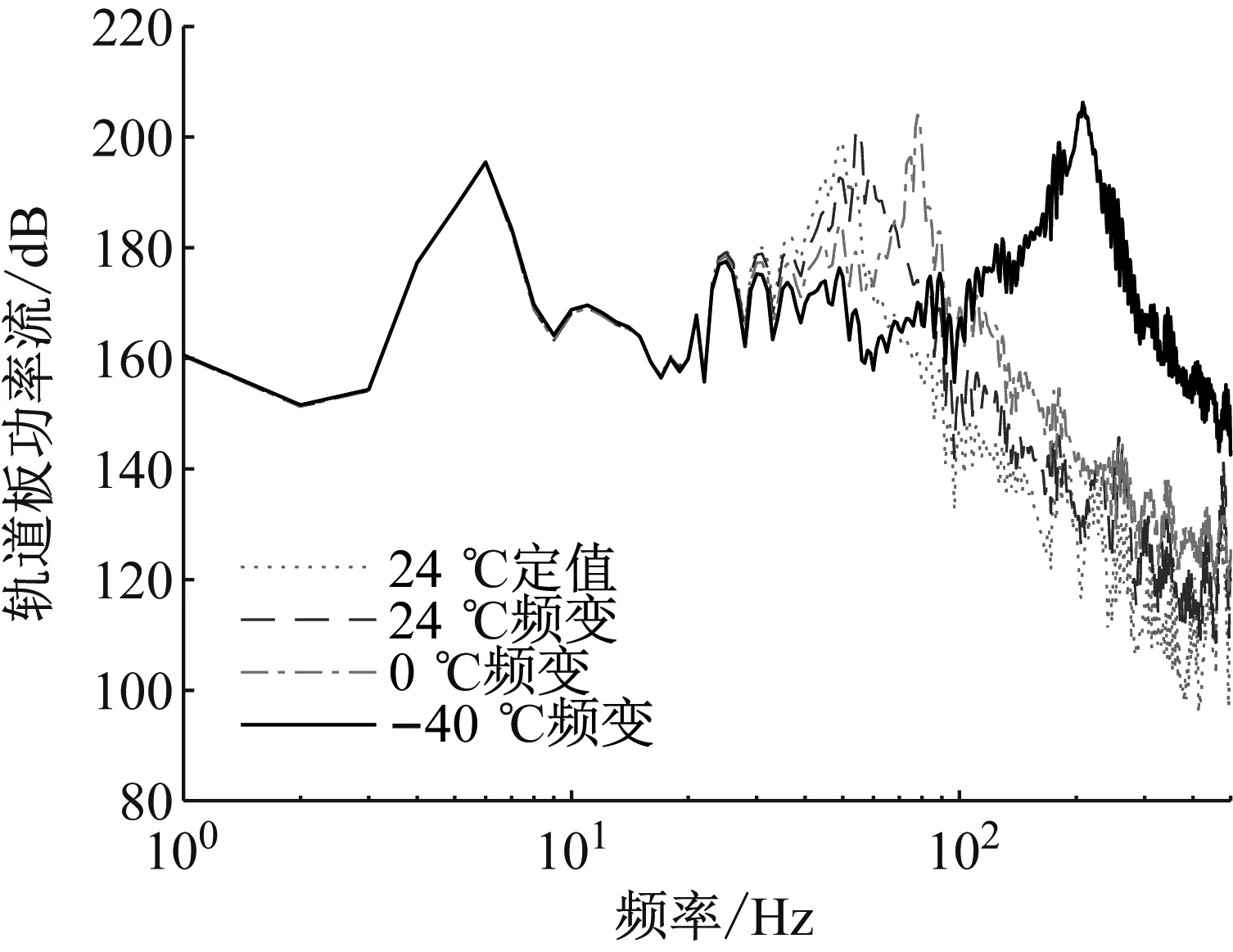
图8 轨道板振动能量图Fig.8 Vibration energy diagram of track plate

图9 桥梁振动能量图Fig.9 Bridge vibration energy diagram

3.2 轨道结构平均振动能量级分析

在频域范围内，由于扣件温频变特性对钢轨、轨道板、桥梁等不同轨道结构的振动能量的影响有所不同，各个结构在不同频段范围内的增减趋势也不尽相似，使用单一的功率流值进行描述具有一定的局限性，其并不能完整的体现轨道结构总体振动能量特性。而平均振动能量级(AELV)因其可从整体上反映轨道结构的振动能量，故被提出用来系统地评价轨道结构总振动能量，平均振动能量级表达式为

(25)

式中，m为功率流计算频率点的数量。

表4为考虑扣件温频变特性后钢轨、轨道板和桥梁的平均振动能量级。由表4可知，24 ℃常温下考虑扣件频变特性后钢轨、轨道板与桥梁振动能量分别增加了2.64%、5.99%、8.06%。-40 ℃低温条件与24 ℃常温条件相比，钢轨、轨道板与桥梁振动能量分别增加了6.02%、22.64%、38.35%。从总振动能量的角度看，温度的降低和考虑扣件频变特性后，轨道结构的振动能量明显增大，其中考虑扣件温频变特性后轨道板与桥梁的振动能量振幅较为明显，而对于钢轨振动能量影响较小。

表4 平均振动能量级

3.3 轨道结构振动能量传递率分析

为了更直观的表达振动能量的竖向传递特性，使用功率流传递率从整体上对车辆-轨道-桥梁耦合系统振动能量传递特性进行评价，功率流传递率表达式为

(26)

图10为钢轨-轨道板的振动能量传递率。从图中可以发现，四种不同工况下钢轨至轨道板的振动能量传递率差别较大，24 ℃常温下考虑扣件频变特性后钢轨至轨道板的振动能量传递率峰值由1.0降低为0.97，且在143 Hz后钢轨至轨道板的振动能量传递率有所增加，最多增大约20.6%。-40 ℃低温条件与24 ℃常温相比，钢轨至轨道板的振动能量传递率在61 Hz后开始增大，最多增大约46.03%。这说明考虑扣件频变特性后在中高频范围内增加了钢轨传递给轨道板的振动能量。

图10 钢轨-轨道板振动能量传递率图Fig.10 Energy transfer rate diagram of rail track plate vibration

图11为桥梁的振动能量传递率。从图中可以发现，不同工况下计算的轨道板至桥梁振动能量传递率，在100 Hz以内的中低频段几乎无明显变化，而在中高频段内振动能量传递率随温度的降低而增大，但是频变工况和温变工况下轨道板到桥梁的振动能量传递率相差较小，这说明扣件温频变动态特性对轨道板-桥梁的振动能量传递率影响不大。

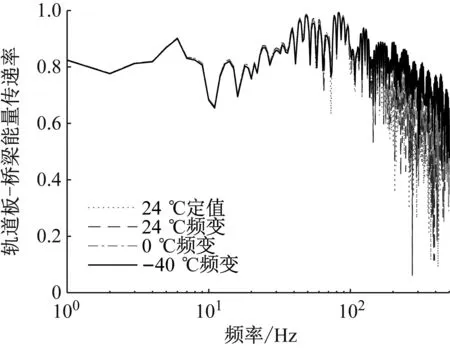
图11 轨道板-桥梁振动能量传递率图Fig.11 Energy transfer rate diagram of track slab bridge vibration

4 结 论

本文对扣件进行定频变温试验，结合温频等效原理与高阶分数导数FVMP模型建立钢轨扣件的温频变动态力学模型，并将此新型扣件模型嵌入车辆-轨道-桥梁垂向耦合系统中，基于功率流法系统地分析与评价扣件温频变动态力学特性对车轨桥耦合系统振动能量分布与传递的影响。所得结论如下：

(1) 扣件的储能模量与损耗因子对环境温度和激振频率具有依赖性。储能模量值随温度升高先小幅下降后陡然降低，且降速逐渐缓和；激振频率的增大也将导致扣件模量值与损耗因子的增大。

(2) 考虑扣件动参数频变会使中高频段内得轨道结构振动能量增大，对低频段内的轨道结构振动能量影响较小，且会使轨道结构振动能量向高频区域偏移；温度的降低会增大扣件的刚度与损耗因子，导致轨道结构的振动能量向高频偏移，且会使轨道结构功率流在中高频范围内增大

(3) 温度的降低会导致轨道结构的振动能量增大，其中轨道板与桥梁的振动能量增幅明显；考虑扣件动参数频变特性后，输入轨道结构的振动能量也会明显增大。从整体能量的角度而言，扣件温频变特性对轨道结构振动能量的分布有较大影响。

(4) 考虑扣件的频变特性后钢轨传递给轨道板的振动能量在143 Hz后的中高频段明显增加，但对桥梁的振动能量传递影响较小；温度的降低会导致钢轨传递给轨道板振动能量在61 Hz后的中高频段增大，但其同样对桥梁的振动能量传递影响较小。从能量传递的角度而言，扣件温频变特性对于钢轨传递给轨道板的振动能量影响较大，而对桥梁的振动能量传递影响较小。

(5) 由于橡胶材料在低温下的硬化现象，轨道结构的振动能量会增大并向高频移动。而且温度-频率相关的放大效应会容易造成寒冷地区的轨道系统中由扣件向下传递的能量的增大，从而引起扣件下部结构的伤损破坏。