高速列车谐波转矩振动分析及自抗扰控制
2022-01-27李伟平邬平波石怀龙朱万刚张玉忠
李伟平, 魏 静, 邬平波, 石怀龙, 朱万刚, 张玉忠
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.西南交通大学 牵引动力国家重点实验室,成都 610031; 3.太原重工轨道交通设备有限公司,太原 030001)
高速列车上大功率异步电机一般采用交-直-交的方式供电,电压、电流中除了含有驱动异步电机所需的基波分量,还含有频率与振幅不一样的谐波电压与谐波电流[1-2],使电机输出谐波转矩造成齿轮箱振动加剧[3-4],当路面不平顺、车轮磨耗或者列车由明线运行到突然进入隧道均可能会引起谐波转矩[5-6]。
赵心颖等[7-8]建立了高速列车牵引传动系统的机电耦合模型,研究异步电机谐波转矩输出对牵引齿轮箱振动行为的影响。孙刚[9]研究了传动系统对车辆各结构的动力学响应影响。Wu等[10]牵引齿轮箱壳体在无转矩、理想转矩和谐波转矩情况下的振动加速度进行了计算和分析,结果表明牵引转矩对振动加速度和动应力有放大作用。Zhang等[11]基于传统的车辆-轨道耦合动力学理论和齿轮动力学理论建立了机车-轨道耦合动力学模型,考虑了齿轮传动系统的动态影响,将仿真实测数据对比验证了该模型的准确性。赵心颖等建立其四阶扭转-弯曲振动模型,对牵引电机输出转矩谐波成分进行了分析,提出了基于误差电压死区补偿的振动抑制策略。Qi等[12]的研究表明了牵引电机谐波转矩将导致牵引传动系统纵向振动异常。黄冠华等[13]建立了考虑齿轮啮合的高速列车动力车整车动力学模型,认为谐波转矩不仅会增大轮齿的角加速度和啮合力,同时使齿轮箱的振动加剧,并改变系统的振动主频,可能引发共振。Winterling等[14-15]指出了电机谐波转矩特性与传动系统的耦合关系。以上研究定性地说明谐波转矩会影响传动系统振动特性,但未给出具体影响规律。
抑制牵引传动系统振动、规避可能发生的共振、降低振动噪声是当前高速列车传动系统振动研究的重点和难点。限于被动隔振方法减振效果局限性、高速列车运行边界条件的复杂性以及考虑到轮轨磨耗和参数蜕化的特点,半主动、主动悬挂技术可以进一步提高优化高速列车的动力学响应,例如采用半主动和主动式横向减振器[16-17]、具有频变特性的转臂定位橡胶节点[18]、刚度阻尼可调式抗蛇行减振器[19]等。有学者对直流环节采用补偿控制来抑制直流电压脉动对电机侧的影响,Gou等[20-21]提出了一种基于频率补偿的中间直流回路故障容错控制算法,抑制中间直流电压脉动对电机侧的影响,该方法需要精确检测直流环节电压脉动幅值。
本文建立考虑时变啮合刚度、啮合阻尼、啮合误差、齿侧间隙的齿轮传动系统与三相异步动态电机耦合的机电传动系统模型,主要研究了电机输出变谐波转矩工况下齿轮箱输入端的振动加速度变化,然后利用自抗扰控制(active disturbance rejection control,ADRC)方法对电机输出谐波转矩引起的横向振动进行了有效抑制。
1 牵引传动系统建模
1.1 传动系统参数
250 km/h“复兴号”某型标准动车组其中一传动系统模型如图1所示。三相异步电动机作为驱动电机将扭矩和转速通过联轴节传递给齿轮箱,经过单级斜齿轮副减速增矩,并最终驱动高速列车轮对。其中齿轮箱处的轴承编号为1~5。

图1 传动系统模型Fig.1 Transmission system model
传动系统参数如表1所示。

表1 传动系统参数
轴承各方向刚度值如表2所示。

表2 轴承刚度
1.2 异步电机模型
利用Clark坐标变换和Park变换将三相异步牵引电机静止坐标系下的非线性微分方程组转化为以转子磁链定向的同步旋转坐标系M-T下的数学模型。鼠笼式异步牵引电机的电压方程为
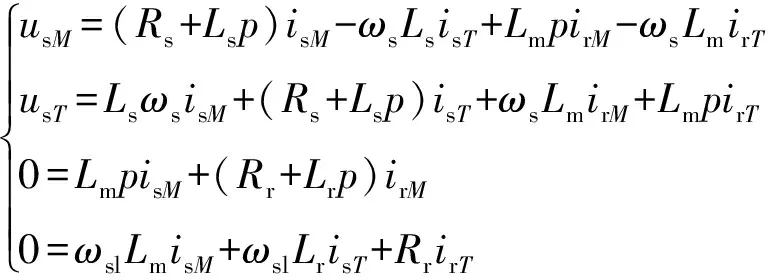
(1)
式中:usM、usT为定子M轴和T轴的电压;isM、isT为定子M轴和T轴的电流;irM、irT为转子M轴和T轴的电流;Rs、Rr为定子和转子电阻;Ls、Lr为定子和转子自感;Lm为定转子绕组间互感;ωs、ωsl为定子电流角频率与定转子转角差频率;p为微分算子,p=d/dt。
磁链方程可表示为

(2)
式中:ΨrM为M轴上的转子磁链分量;ΨrT为T轴上的转子磁链分量;Ψr为转子磁链。
电磁转矩表达式为
(3)
式中,np为极对数。
异步电机运动方程为
(4)
式中:TL为负载阻力矩;J为旋转机组的转动惯量;ωr为电机转子电角速度。
异步电机参数如表3所示。
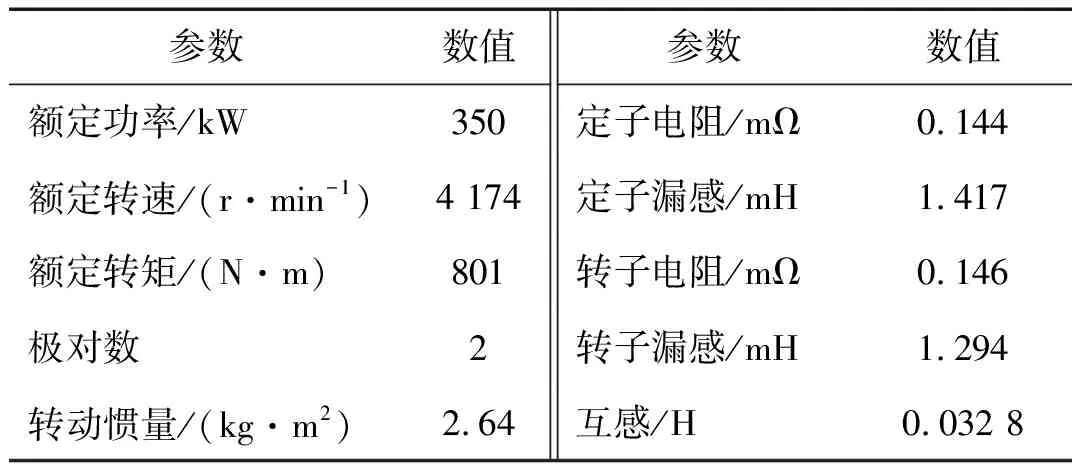
表3 异步电机参数
1.3 齿轮传动系统动力学建模
高速列车牵引齿轮箱斜齿轮副在传动过程中,由于轮齿啮合力会产生一个轴向分力,因此系统产生扭转振动、横向振动和轴向振动。在综合考虑齿轮时变啮合刚度、啮合阻尼、啮合误差和齿侧间隙的影响下,建立齿轮传动系统的弯扭轴耦合动力学模型,啮合单元模型如图2所示。
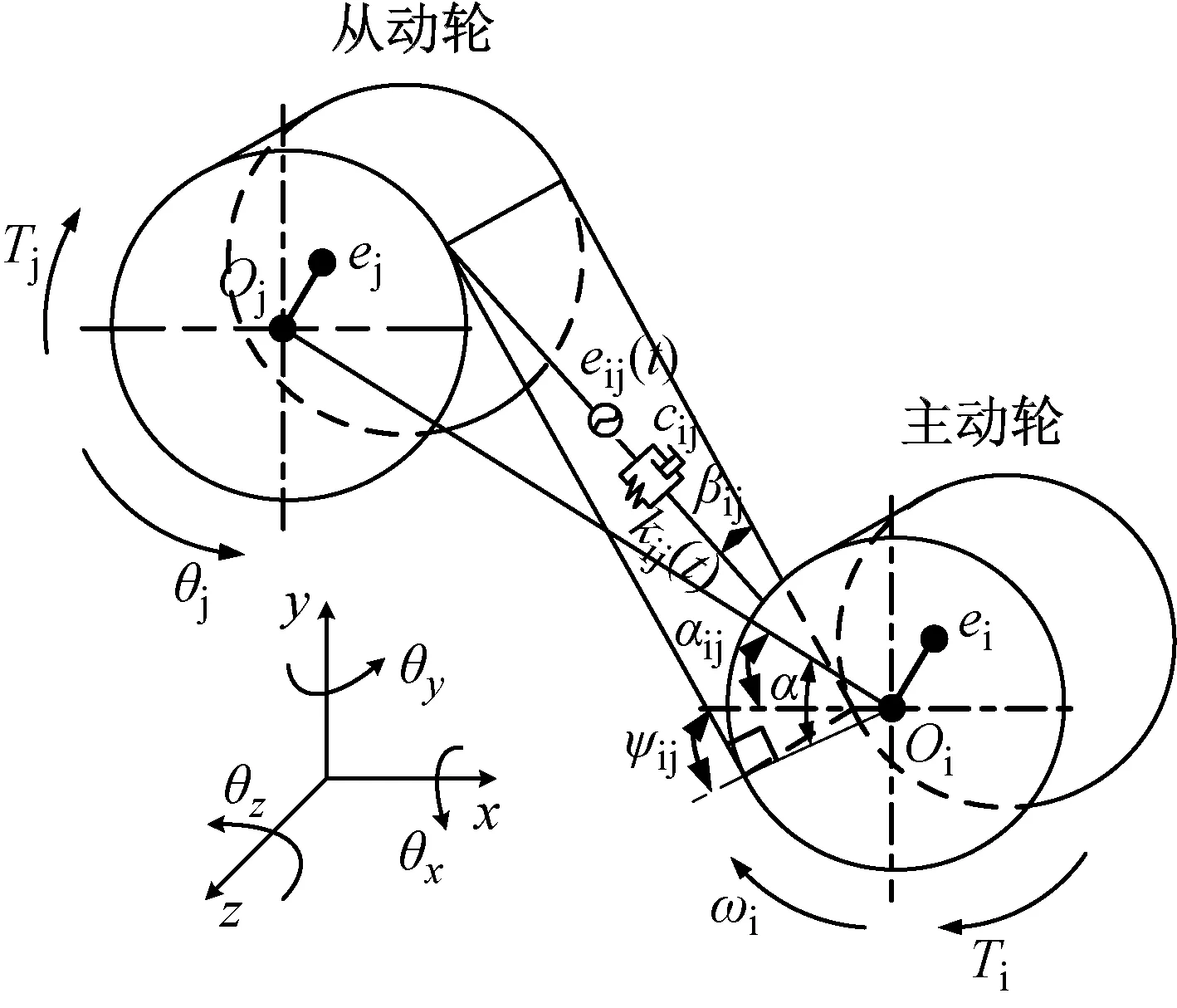
图2 斜齿轮副啮合模型Fig.2 Helical gear meshing model
考虑齿轮x,y,z三个方向的移动自由度和z向的旋转自由度,以及电机端和负载端的扭转自由度,设啮合刚度为km,啮合阻尼为cm,支撑刚度为kab(a=i, j;b=x,y,z),支撑阻尼为cab(a=i, j;b=x,y,z),轴的扭转刚度为kn(n=p, r),扭转阻尼为cn(n=p, l),齿侧间隙为gij,啮合误差为eij,齿轮副中心线与x轴正向的夹角为αij,Ψij是轴y正向到啮合面的方向角。下标i,j分别表示主、从动齿轮,下标m表示电机端,下标l表示负载端,下标p, r分别表示输入轴和输出轴。
定义系统广义位移矩阵为
{δ}={θm,x1,y1,z1,θ1,x2,y2,z2,θ2,θl}T
(5)
主动轮左旋顺时针转动时的啮合线位移为[22]
δij=cosβisinαijxi-cosβicosαijyi+sinβ1zi-
Ricosβiθi-cosβjsinαijxj+cosβjcosαijyj-
sinβjzj+Rjcosβjθj-eij+gij
(6)
建立齿轮传动系统动力学方程

(7)
式中:m为质量;J为转动惯量;T为扭矩;Ri、Rj分别为主、从动齿轮基圆半径。
啮合误差和齿侧间隙分别采用简谐函数和分段式函数模拟[23]。啮合误差计算公式为
eij(t)=Etsin(2πωit+φs)+
Essin(2πωmt+2πγs)
(8)
式中:Et为齿轮副齿距累积总偏差;Es为齿轮副一齿切向综合偏差;ωi为主动轮所在轴的轴频;φs为齿轮轴频的初相位;ωm为齿轮副的啮频;γs为啮频的初相位。
齿侧间隙计算公式
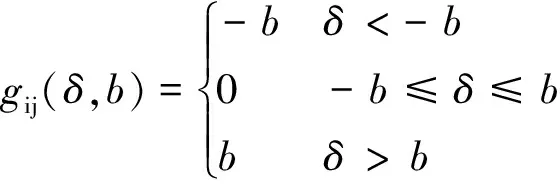
(9)
式中,b为啮合齿侧间隙。最小齿侧间隙为
(10)
啮合阻尼计算公式[24]
(11)
式中,ξg为轮齿啮合阻尼的阻尼比,取0.1。
电机端动力学方程为
(12)
负载端动力学方程为
(13)
2 机电耦合仿真
基于Simulink平台建立异步动态电机与齿轮箱耦合模型,三相逆变器控制信号的产生采用的是两电平空间矢量脉宽调制(SVPWM)控制策略,SVPWM能够十分显著地减小逆变器输出电流的谐波成分,使得输出电磁脉动转矩降低。耦合仿真模型如图3所示。

图3 Simulink仿真模型Fig.3 Simulink simulation model
2.1 异步电机输出分析
异步电机转速如图4所示,因为电机转子转动惯量和负载车轮的转动惯量较大,空载启动3 s过后电机转速经过超调回落到额定速度运行。3.5 s时添加负载,转速略有跌落然后逐渐恢复到额定转速稳定运行。

图4 电机输出转速Fig.4 Motor output speed
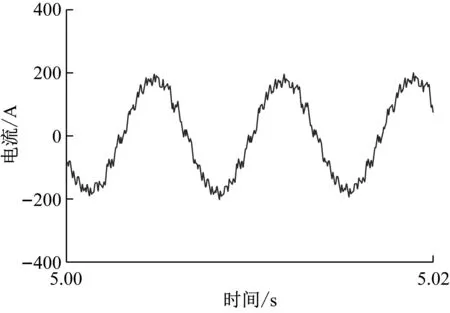
额定工况下电机定子A相电流时域图和电磁转矩时域图分别如图5(a)和图6(a)所示,对应的频域分析分别如图5(b)和图6(b)所示。
(a) 时域图

(b) 频域图

(a) 时域图

(b) 频域图图6 电磁转矩Fig.6 Electromagnetic torque
从图5(b)可以看出,定子电流基频的幅值为177 A,其它较大幅值的频率有fs-fn、fs+fn、5fs、7fs、11fs、13fs、17fs、19fs、23fs和25fs,谐波幅值最大的是电流的13次谐波频率,其中fn表示电机转子轴频、fs为定子电流基频。由于采用三相逆变器,定子电流频谱包含6n±1倍电流基频的谐波成分。从图6(b)可以看出,电磁转矩谐波成分中轴频峰值最大,主要谐波成分为6n倍电流基频,还存在斜齿轮副啮合频率fm。
2.2 齿轮箱振动加速度分析
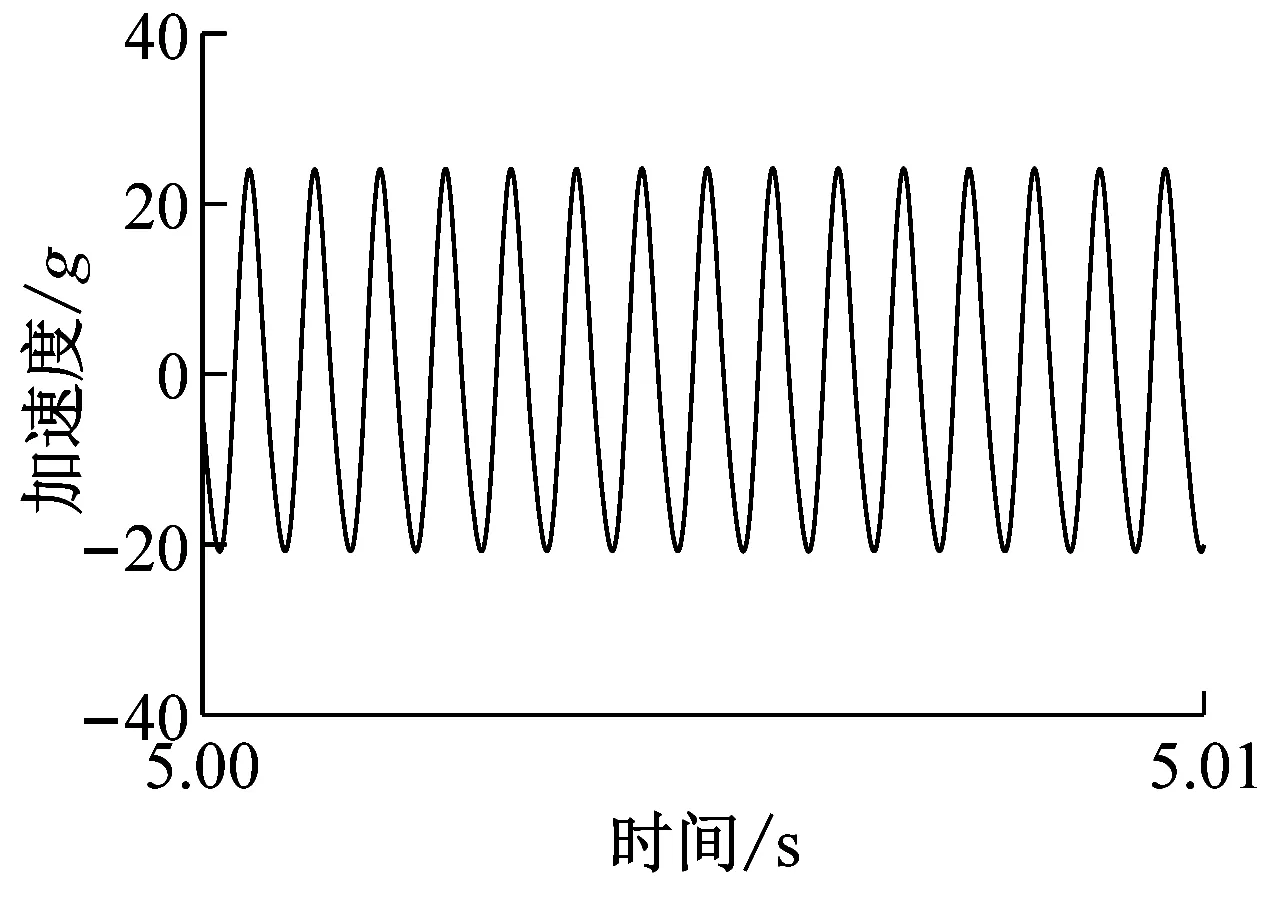
将齿轮的振动加速度折算到轴承孔处,限于篇幅,选取牵引齿轮箱靠近电机输出端的轴承孔处振动加速度进行分析。额定稳态运行工况下轴承孔x、y、z向振动加速度时/频域如图7所示。

(a) x向时域

(b) x向频域
(c) y向时域

(d) y向频域

(e) z向时域

(f) z向频域图7 振动加速度图Fig.7 Vibration acceleration graph
x、y、z三个方向振动加速度频谱中均明显含有fn、fm、6fs、fm、2fm、3fm以及fm、2fm与fn组成的边频带谐波成分。fm是三个方向谐波幅值最大的频率,其中y向的fm幅值是三个方向啮合频率中最大值,瞬时值能够达到15g;其次是z向,瞬时最大值为2.6g;x向振动加速度瞬时最大值为1.4g。
对比图6(b)可知,振动加速度谐波成分与电机输出转矩的谐波成分密切相关,且系统垂向(y向)的谐波振动加速度值比另外两个方向的值更大,是系统振动加速度的主要部分。
2.3 谐波转矩激励下振动加速度分析
高速列车在输入电压受到扰动和复杂外部运行环境下会产生附加谐波转矩,此节具体分析谐波转矩变化对耦合系统的影响。以额定转矩的0、20%、40%、60%、80%作为附加谐波转矩的幅值叠加到电机输出转矩上,并进行对比分析。
2.3.1 对定子电流和输出转矩的影响
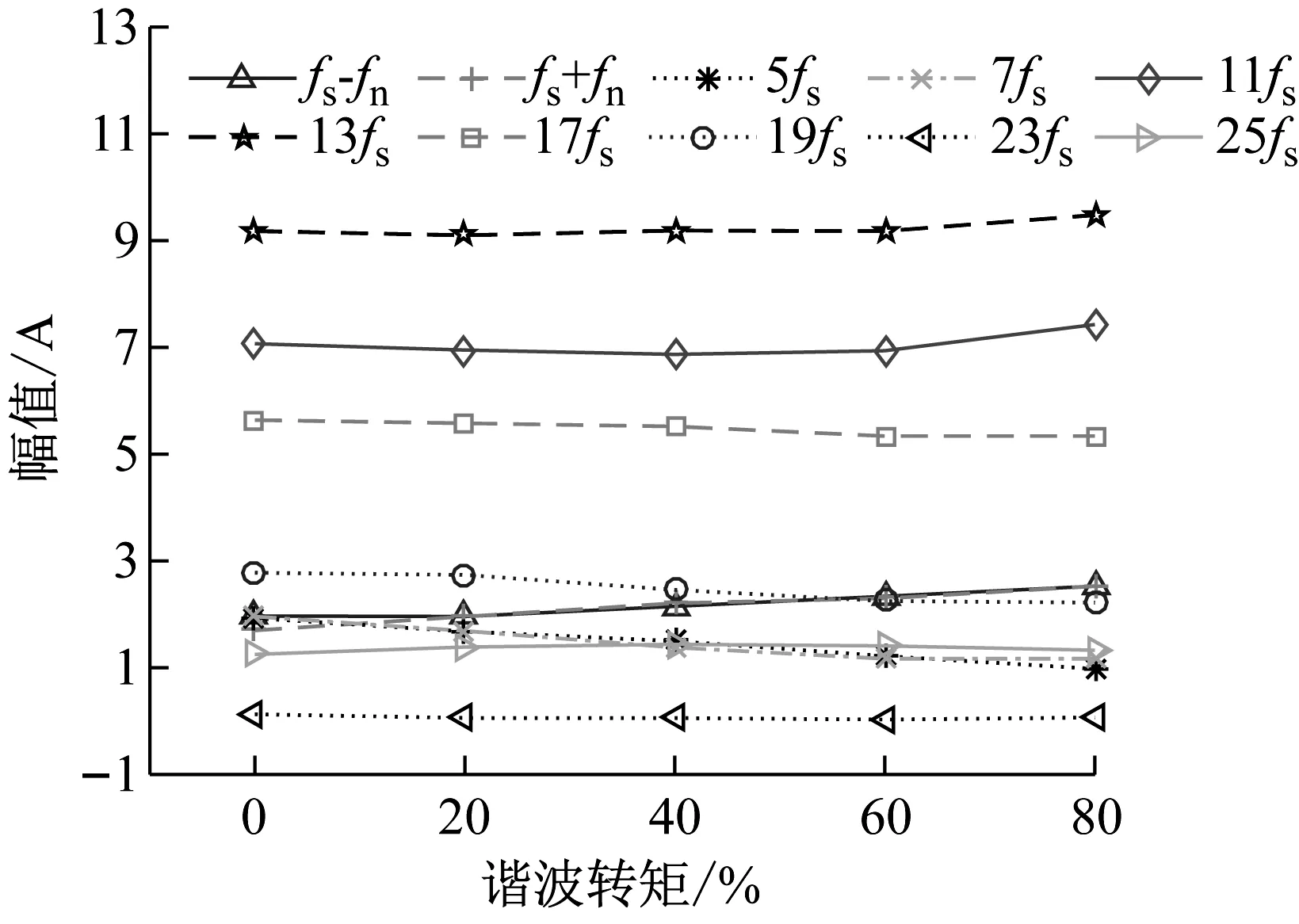
当附加谐波转矩幅值从电机额定转矩值的0增加到80%时,电机定子电流各谐波幅值变化和电磁输出转矩各谐波幅值变化如图8所示。
从图8(a)可以看出,随着附加谐波转矩幅值百分比不断增加,电机定子电流谐波成分除5fs、17fs和19fs的幅值略有减小,其它成分谐波幅值均有不同程度的增大,因此附加谐波转矩幅值逐渐增加会引起定子电流部分谐波幅值增加。
(a) 定子电流变化图

(b) 电磁转矩变化图图8 谐波幅值变化图Fig.8 Harmonic amplitude variation graph
分析图8(b)知道,随着附加谐波转矩幅值百分比不断增加,电机输出转矩谐波成分中fn的幅值呈现持续上升趋势;12fs和24fs的幅值增长幅度较小;6fs和18fs的幅值有着缓慢减小趋势;fm的幅值变化不明显。说明附加谐波转矩幅值逐渐增大,电机输出转矩波动也逐渐加大。
2.3.2 对齿轮箱振动加速度的影响
同样,选取靠近电机输出侧齿轮箱轴承孔进行分析。为了分析振动加速度随谐波转矩改变的变化趋势,采用频谱曲线与频率轴围成的面积作为衡量指标。x、y、z三个方向振动加速度频谱曲线与频率轴围成的面积随附加谐波转矩幅值比例增加的增大值和增长率如图9所示。

(a) 增加值

(b) 增长率图图9 振动加速度对比图Fig.9 Comparison of vibration acceleration
根据图9可知,当附加谐波转矩幅值增加时,齿轮箱输入位置每个方向振动加速度也在不断增大。不同方向振动加速度增加比率不同,z向增加比率最大,谐波转矩幅值每增大20%,振动加速度谐波幅值累计值增加率约为6.4%;x向其次,谐波转矩幅值每增加20%,振动加速度谐波幅值累计值增加率在3%左右;而y向增加很小,可以认为基本不变。
由此说明谐波转矩对牵引传动系统振动横向(z向)影响很大,这也表明谐波转矩的存在和加大会严重影响列车向前行驶时的稳定性;而谐波转矩对牵引传动系统振动纵向的影响不是很大,对垂向的影响可以忽略。
从图7可知,斜齿轮副啮合频率及其倍频是系统振动加速度的主要谐波成分,谐波转矩加大也会增大啮合力。斜齿轮副动态啮合力频谱曲线与频率轴所围成的面积大小增加值和增长率随着谐波转矩幅值增加的变化如图10(b)所示。

(a) 动态啮合力频域

(b) 增加值与增长率图图10 动态啮合力及其变化图Fig.10 Dynamic mesh force and its variation
动态啮合力谐波成分主要包含轴频、啮频及其倍频和啮频及其啮频与轴频形成的边频带,由图8(b)可知,谐波转矩增加会引起轴频谐波幅值增大,则动态啮合力也会增加。由图10(b)可以看出,当谐波转矩幅值增加时,斜齿轮动态啮合力随着附加谐波转矩幅值的增加而增大,但是增大程度不同。当谐波转矩由20%增加到40%时,啮合力增加值为346 N,增大率为4.3%,其它情况下增加值均大于2%。即谐波转矩从0%上升到80%过程中啮合力不断增加,增长率先升高后降低。
3 基于ADRC的电流补偿减振策略
3.1 混合型自抗扰控制
考虑到电机内部非线性因素和牵引传动系统内外复杂激励,使用混合型自抗扰控制(ADRC)电流补偿策略来减小牵引传动系统振动加速度。利用线性扩张状态观测器(LESO)估计扰动,实时动态跟踪补偿,在PI控制的T轴上叠加补偿电流,将因内外部非线性扰动产生的可能振动从电气控制部分进行抑制。扰动消除环节采用非线性状态误差反馈(NSLEF),得到一阶混合型自抗扰控制原理如图11所示。

图11 混合型自抗扰控制原理Fig.11 Principle of ADRC
LESO被控对象为[25]
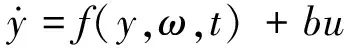
(14)
式中:y、u分别为输出与输入;ω为外扰作用;f(y,ω,t)为包括外扰和内扰的总扰动。
选取状态变量:x1=y,x2=f,将式(14)转化为连续的扩张状态空间

y=Cx
(15)
式中:E[0 1]T;C=[1 0]。
对应的连续线性扩张状态观测器为
yc=z
(16)

λ(s)=|sI+LC|=(s+ω0)2
(17)
式中,I为单位矩阵。
采用非线性状态误差反馈消除扰动,形式如下
(18)
式中:α(0<α≤1)为非光滑系数;δ为线性范围;β为比例系数。
自抗扰控制器输出为
(19)
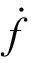
将电机轴两端的转速差作为观测目标,以转速差Δω=0作为控制目标,实时观测转速差并计算出系统所需的补偿电流将其直接叠加在转速环输出电流上。
3.2 结果分析
额定工况扩张状态观测器对转速差跟踪估计值与实际值的对比如图12所示。所设计的扩张状态观测器能够很好地跟踪转速差实际值,误差很小。
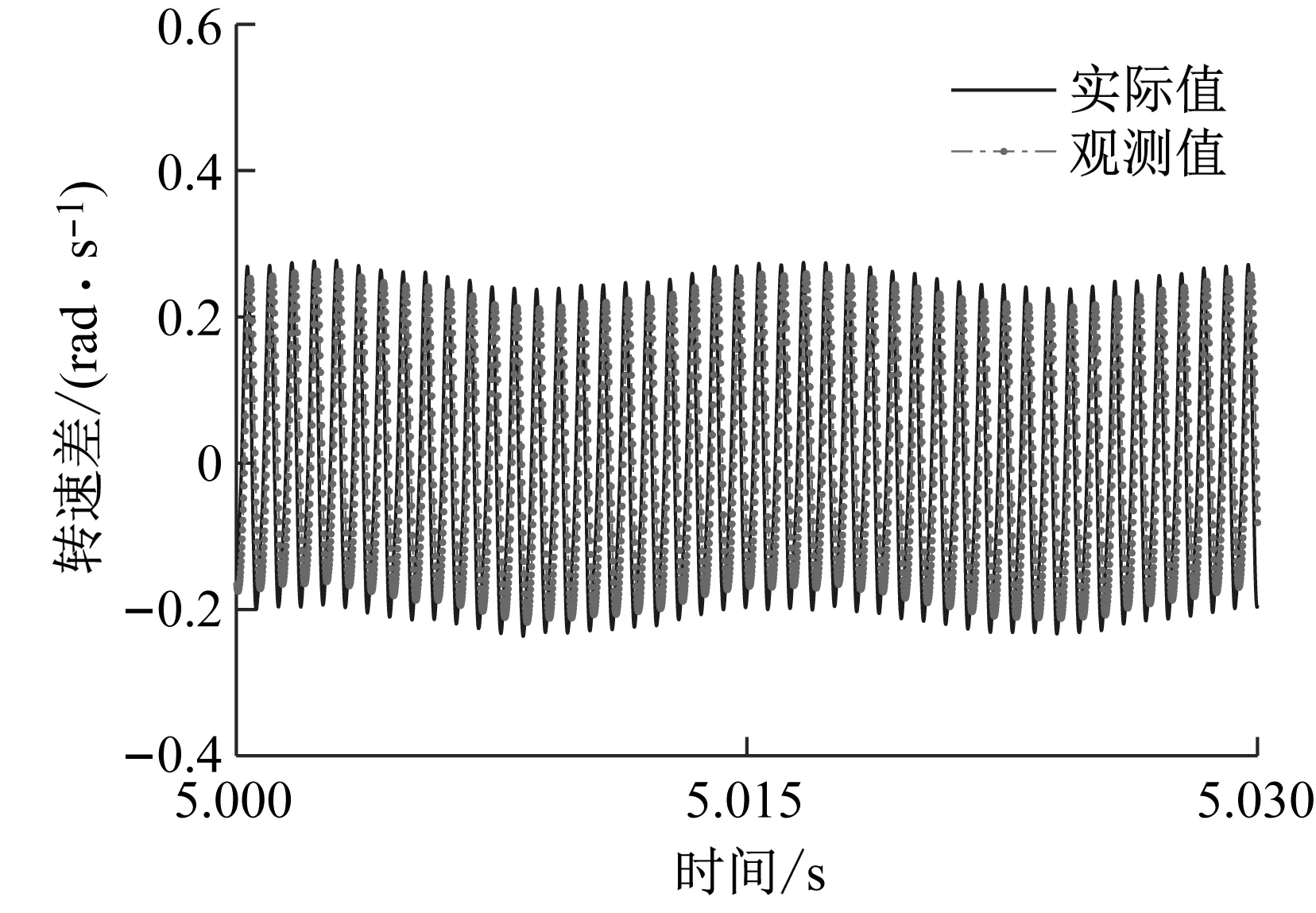
图12 观测值与实际值对比Fig.12 Comparison of observed and actual values
额定工况下电机输出转速对比如图13所示,说明在ADRC电流补偿策略下不改变电机输出转速,同时转速比纯PI控制下波动更小。ADRC与PI控制下电流频谱曲线与频率轴围成的面积对比图如图14所示。

图13 转速对比图Fig.13 Speed comparison graph

(a) 定子电流对比图
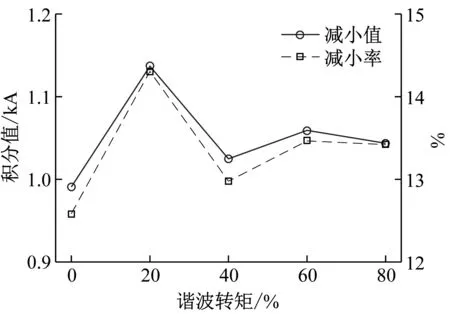
(b) 定子电流减小值与减小率图14 定子电流随转矩谐波变化图Fig.14 Stator current changes with torque harmonics
随着谐波转矩增大,ADRC控制下定子电流频谱曲线与频率轴围成面积比PI控制下面积有所减小,20%谐波转矩时降低最大,达到了14.3%。
ADRC策略下与PI控制下的斜齿轮副动态啮合力对比如图15所示。其中,图15(a)为60%谐波转矩的时域图。

(a) 啮合力时域图

(b) 啮合力对比图
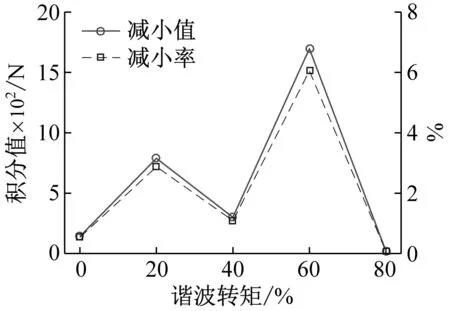
(c) 啮合力减小值与减小率
ADRC策略对不同谐波转矩的啮合力减小幅度差异较大,对20%、40%和60%谐波转矩下啮合力的谐波成分减小最为明显,而对0%和80%谐波扭矩下无显著减小。图16是在80%谐波转矩情况下z向振动加速度频谱分析对比图。
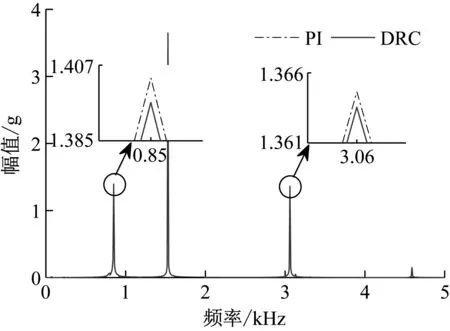
图16 z向振动加速度频谱图Fig.16 Spectrum of vibration acceleration in z direction
采用ADRC策略后,振动谐波峰值比纯PI控制有所降低。采用面积法分析谐波转矩幅值分别为额定转矩值的0%,20%,40%,60%,80%时振动加速度的抑制情况。随着谐波转矩增加ADRC控制下与PI控制下的面积值如图17(a)所示,ADRC控制下减小值与减小率如图17(b)所示。

(a) 振动加速度对比

(b) 减小值与减小率图17 ADRC与PI对比Fig.17 Comparison of ADRC and PI
从图17(a)可知,在不同百分比谐波转矩下,ADRC策略下的齿轮箱横向振动加速度值均小于PI 控制下的振动加速度,说明ADRC在不同谐波转矩情况下均可减小振动。从图17(b)可知,谐波转矩从0%增加到80%过程中,抑振效果先降低后升高。在40%谐波转矩下的抑振效果略差,80%谐波转矩下的抑振效果最好。
4 结 论
本文建立考虑时变啮合刚度、啮合阻尼、啮合误差、齿侧间隙的高速列车齿轮传动系统与三相异步动态电机耦合的机电传动系统模型,开展了谐波转矩振动分析及自抗扰控制研究,具体结论如下:
(1) 振动加速度谐波成分与电机输出转矩的谐波成分密切相关,而且系统垂向的谐波振动加速度值比另外两个方向的值更大,是系统振动加速度的主要成分。
(2) 谐波转矩对电机定子电流和电磁转矩有一定的影响,谐波转矩幅值增加会导致定子电流和电磁转矩的部分谐波幅值增大;谐波转矩对牵引传动系统横向的振动加速度影响很大,对纵向和垂向的振动加速度影响很小。
(3) 所提出的ADRC电流补偿策略对谐波转矩导致的传动系统啮合力谐波成分增加具有很好的减小作用,特别是在60%谐波转矩时;同时ADRC策略对传动系统横向振动加速度有较好的减振作用,且在80%谐波转矩时的抑振效果最好。
