基于EEMD和参数自适应VMD的高速列车轮对轴承故障诊断
2022-01-27李翠省廖英英刘永强
李翠省, 廖英英, 刘永强
(1.石家庄铁道大学 交通运输学院,石家庄 050043; 2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)
轮对轴承是列车走行部中关键的旋转部件之一,起着支撑、传动、运动转换等重要作用,其运行状态直接关系到列车的运行安全[1-2]。因此,对轮对轴承进行故障诊断研究具有重要的意义。
轮对轴承长期处于高速重载的运行环境中,承受着多种交变载荷的作用,同时还受到踏面磨耗、轨道不平顺等外部复杂激励的影响。所以轴承元件的工作表面极易出现压痕、点蚀、剥落等局部损伤[3]。这些故障冲击响应被强烈的背景噪声所淹没,通常无法直接识别。因此,在复杂干扰下准确分离与识别出故障特征,是轮对轴承故障诊断的重点和难点。
针对这一难点,学者们提出了多种分析方法,比如共振解调法,短时傅里叶变换,小波变换等,其中重要一类就是信号分解方法[4]。经验模态分解(empirical mode decomposition,EMD)[5]是一种自适应信号处理方法,可将非平稳信号分解成不同频段的模态分量,在信号处理中应用较广,但EMD存在端点效应、模态混叠等问题[6]。集成经验模式分解(ensemble empirical mode decomposition, EEMD)是EMD的一种改进算法,能有效抑制模态混叠现象[7]。局部均值分解(local mean decomposition,LMD)[8]改善了EMD中过包络或欠包络的问题,但其本质与EMD、EEMD一样都属于递归式模态分解,终究避免不了端点效应和模态混叠现象。Dragomiretskiy等[9]根据约束性变分问题,提出了一种非递归式模态分解方法,即变分模态分解(variational modal decomposition,VMD),可有效减少模态混叠现象的发生。该算法可以将信号在频域内灵活分割,能有效挖掘信号中被噪声淹没的故障特征信息。一经提出,受到国内外众多学者的关注[10-11]。
学者们研究发现,VMD对信号的处理效果受其自身参数设置的影响。文献[12]通过中心频率观察法确定分解模态数,实现了滚动轴承故障特征提取;文献[13]利用奇异值最佳有效秩阶次来确定分量个数,用于风电齿轮箱故障分析。上述文献在应用VMD时,仅考虑了模态数K的影响,而忽略了二次惩罚因子α对模态带宽的影响[14]。目前流行方式之一是通过引入智能优化算法,来自适应地确定[K,α]参数组合。如文献[15]采用混合灰狼进化算法,以局部最小包络熵为目标函数优化VMD参数;文献[16]提出了基于相关峭度和蝗虫优化算法的参数自适应VMD方法。不难发现,基于智能优化算法的参数自适应VMD方法的关键在于确定合适的目标函数,引导全局寻优。倘若目标函数确定不恰当,将导致寻优失败。如上文提到的包络熵指标,其对异常尖脉冲比较敏感,当信号中存在该项干扰时,优化后的VMD将不能准确提取出轴承的故障特征信息。为提升目标函数的抗噪性,学者们经过不断探索,提出了一些先进指标。文献[17]提出了加权峭度指标(weighted kurtosis index,KCI),文献[18]提出了全体峭度指标(ensemble kurtosis index,EKI),文献[19]提出了融合冲击指标(syncretic impact index,SII),均取得了不错的效果。然而,高速列车轮对轴承工作环境复杂,振动信号中时常伴有冲击性噪声和循环平稳性噪声。笔者研究发现,在这些强干扰存在的环境中上述三种先进指标依然会受到影响。
通过上述分析可知,参数自适应VMD方法的核心在于确定合适的目标函数。而在强噪声的环境下,现有的指标又很难避开这些干扰的影响。为此,本文提出了一种基于EEMD预处理的参数自适应VMD方法。首先将原始信号进行EEMD分解,选取包络峭度值大于原始信号包络峭度值的分量进行重构,生成新的信号。其次再以局部最大包络谱峭度作为目标函数,利用粒子群优化算法对VMD进行参数优化。最后使用优化后的VMD对新信号进行分解,选取包络谱峭度值最大的分量进行包络解调分析,可以准确地提取到轮对轴承的故障特征信息。
1 基于EEMD预处理的参数自适应VMD方法
1.1 集成经验模态分解(EEMD)
EEMD是一种基于信号本身时间尺度特征进行自适应分解的方法,其本质是在原信号中加入高斯白噪声,利用白噪声频率均匀分布的统计特性,经多次EMD分解,达到抑制模态混叠的目的。
EEMD具体分解过程如下[20]
(1) 在信号x(t)中加入随机高斯白噪声
xm(t)=x(t)+knm(t)
(1)
式中,k为所加噪声幅值系数。
(2) 利用EMD方法对信号xm(t)进行分解;
(3) 每次加入不同的高斯白噪声序列,重复步骤(1)、(2),直至达到终止条件;
(4) 将分解得到的各个IMF分量的均值记为最终分解结果
(2)
式中:N为加噪声的次数;ci,m表示第m次EMD分解得到的第i个IMF分量。
1.2 VMD算法
VMD是一种完全非递归的信号分解模式,其实质是构造一个受约束的变分模型,通过迭代搜寻最优解。VMD可将一个非平稳的输入信号y分解成K个具有特定稀疏性的模态分量yk,并能确定出每个分量的中心频率ωk和带宽。
算法中通过计算调制信号梯度的L2范数来估计各分量的带宽,其对应的约束变分模型表达式如下
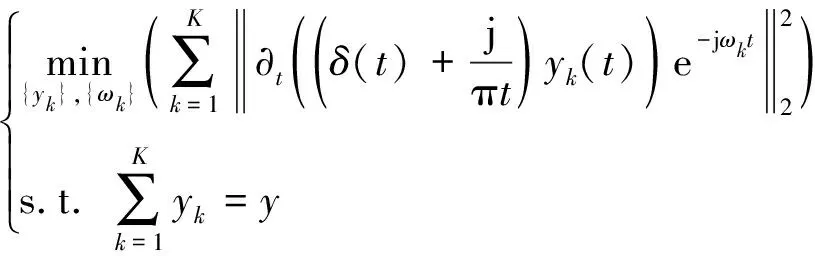
(3)
式中:{yk}表示分量信号;{ωk}表示相应的中心频率的集合;K为分解层数。
引入二次惩罚因子和Lagrange乘子将式(3)转化为无约束优化模型,表达式如下
(4)
式中:α为二次惩罚因子;λ为Lagrange乘子。
对式(4)采用交替乘子算法求其最优解,结果如下
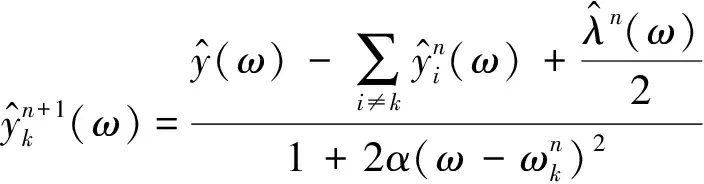
(5)
(6)
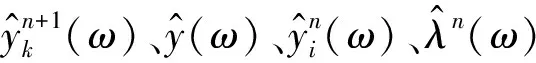
(3) 根据式(7)更新
(7)
(4) 根据式(8)判断是否收敛,若满足收敛条件分解过程结束;否则迭代次数n=n+1,返回步骤(2)继续分解。
(8)
1.3 改进粒子群优化算法
粒子群算法拥有进化计算和群体智能的特点,具有良好的全局优化能力。在一个D维空间中,由m个粒子组成的种群Z={Z1,Z2,…,Zm},每个粒子所处的位置Zi={zi1,zi2,…,zin}都表示一个解,且会根据目标函数搜索新解,每个粒子的速度为Vi={vi1,vi2,…,vin}。每次迭代中,粒子跟踪个体最好解Pid和种群最优解Pgd,根据式(9)来更新自身速度和位置
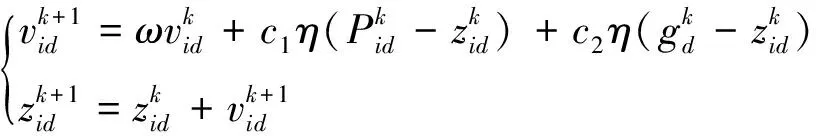
(9)
式中:ω为惯性权重;d=1,2,…,D;i=1,2,…,m;k为当前跌迭代次数;c1和c2为学习因子;η为介于[0,1]间的随机数。
在标准粒子群算法中,随着粒子速度的不断更新会对ω进行动态调整,用于权衡全局和局部搜索能力,线性递减权值策略如下
(10)
式中:Tmax为最大迭代次数;t表示当前迭代次数;ωmax为最大惯性权重;ωmin为最小惯性权重。
粒子群的性能在很大程度上依赖于参数ω、c1和c2的设置,文献[21]在上述标准粒子群的基础上,提出了动态学习因子,成功用于VMD参数优化,公式如下
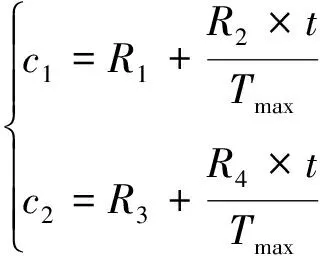
(11)
式中,R1、R2、R3和R4为初始系数值。
文献[22]对惯性权重进行了深入研究,发现凹函数递减策略在不影响收敛精度的前提下,能较大幅度地提升粒子群的收敛速度,整体效果优于线性递减策略。因此,为进一步提升粒子群的优化性能,本文将凹函数递减权值代替式(10),构成新的改进粒子群优化算法,具体公式如下
(12)
根据文献[23],设置改进PSO的具体参数,如表1所示。

表1 粒子群参数
1.4 故障指标性能分析
滚动轴承的故障信号在时域具有冲击性,在频域具有循环平稳性,在进行故障特征提取时需同时考虑这两大特征。顾晓辉等指出振动信号包络的稀疏性可表征轴承故障的冲击性,信号包络谱的稀疏性可表征轴承故障的循环平稳性,对于稀疏性的度量,峭度为最常用指标之一。
信号包络的峭度如式(13)所示
(13)
式中:Ex为信号经Hilbert解调后得到的包络信号;μE为Ex的均值;σE为Ex的标准差。
信号包络谱的峭度如式(14)所示
(14)
式中:ESx=DFT[Ex];μES为ESx的均值;σES为ESx的标准差。
在对轴承故障进行评价时,单一指标易受冲击性噪声或循环平稳性噪声的影响。为此,学者们经过不懈努力,提出了一些新的复合型指标。Zhang等提出了加权峭度指标IKC,公式如下
IKC=KI·|C|
(15)
式中:KI代表信号的峭度;|C|代表相关系数。
Miao等提出了全体峭度指标IEK,公式如下
IEK=KES·K
(16)
式中:K代表信号的峭度;KES代表信号的包络谱峭度。
He等提出了融合冲击指标ISI,公式如下
ISI=KEPS·|CC|
(17)
式中:KEPS代表信号的包络功率谱峭度;|CC|代表相关系数。
为了研究这些指标的性能,用第3章的仿真信号进行分析。仿真信号是由故障冲击、高幅值随机脉冲、周期性干扰和高斯白噪声组成。用上述五种指标对这四种成分进行敏感性分析,如图1所示。我们不难发现,KE和IKC对高幅值随机脉冲敏感,KES、IEK和ISI对周期性干扰敏感。在强干扰环境下,现有的单一或复合型指标都很难统一并平衡轴承故障响应的冲击性和循环平稳性特征。
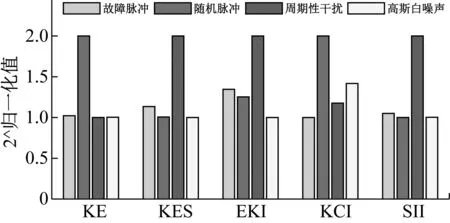
图1 五种指标对不同成分的敏感性Fig.1 Sensitivity of five indexes to different components
2 方法步骤
参数自适应VMD方法有很强的故障特征提取能力,但诊断效果严重依赖于优化算法中目标函数的设置。在冲击性噪声和循环平稳性噪声存在的环境下,现有的故障评价指标又很难避开这些干扰的影响。针对该问题,本文同时考虑到EEMD具有优秀的降噪能力和自适应性[24],为此提出了基于EEMD预处理的参数自适应VMD方法。首先将原信号进行EEMD分解,以包络峭度为评价指标,进行信号重构,可排除循环平稳性噪声的影响,但新信号中仍会存在冲击性噪声;其次再以包络谱峭度为目标函数,优化VMD参数,可消除冲击性噪声的干扰,最终达到精准提取故障特征信息的目的。详细步骤如下:
步骤1将采集到的振动信号进行EEMD分解,计算原信号以及各分量的包络峭度值,选取峭度值大于原始信号峭度值的分量进行重构,生成新的振动信号。
步骤2给定VMD中二次惩罚因子α的寻优范围[100,5 000],模态分解个数K的寻优范围[2,10]。
步骤3根据表1设置PSO中的参数,以局部最大包络谱峭度为目标函数,搜寻VMD的最佳参数组合。
步骤4利用优化后的VMD对新信号进行分解,生成K个分量,选取包络谱峭度值最大的分量,进行包络解调分析,与理论故障特征频率对比,判断轴承故障。
具体诊断流程如图2所示。
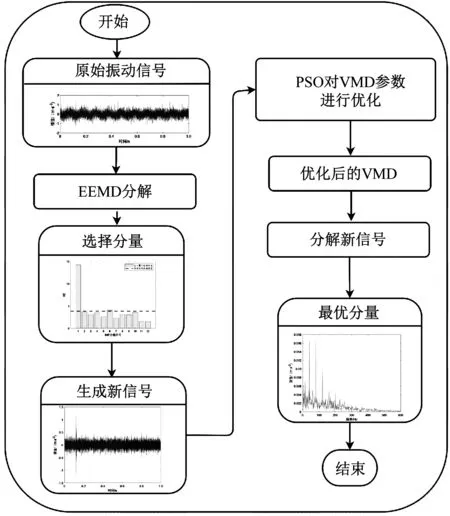
图2 轮对轴承故障诊断流程图Fig.2 The flow chart of wheelset bearing fault diagnosis
3 仿真信号分析
为了验证本文方法的正确性,采用文献[25]中介绍的模拟信号模型,来模拟复杂工况下真实的振动信号。信号中包含四部分:轴承故障引起的重复性瞬态,电磁干扰引起的高幅值随机脉冲,轴旋转和齿轮啮合产生的周期性干扰,以及高斯白噪声。公式如下

(18)
式中:fr代表转频;Z代表齿轮的齿数;Td为故障周期;τi为滚动体的随机滚动误差;S(t)为脉冲响应函数。S(t)的表达式如下
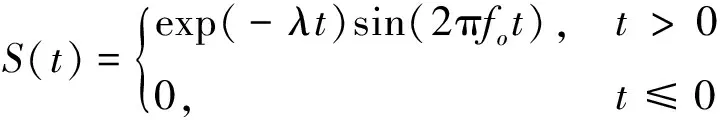
(19)
在式(18)和(19)中用到的具体参数如表2所示,n(t)为均值为0,方差为0.25的高斯白噪声。

表2 仿真信号中的参数
采样频率Fs为10 000 Hz,采样时间为1 s。仿真信号各组成成分如图3所示,图3(a)为轴承故障脉冲信号,图3(b)为高幅值随机脉冲信号,图3(c)为周期性干扰,图3(d)为高斯白噪声。

(a) 故障冲击
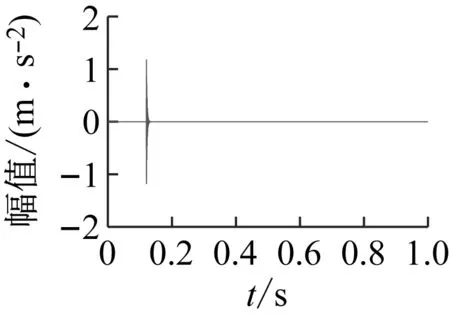
(b) 随机冲击
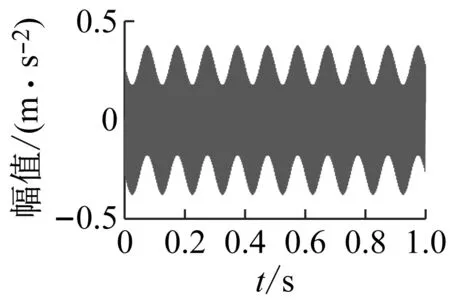
(c) 周期干扰
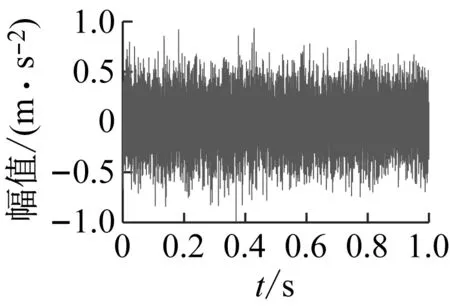
(d) 高斯白噪声图3 仿真信号的四种成分Fig.3 The four components of the simulation signal
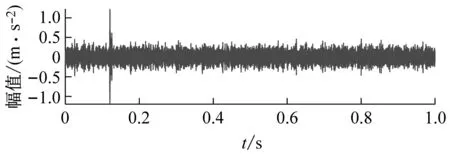
仿真信号的时域波形、频谱以及包络谱如图4所示,在时域波形图中可以看出故障冲击信号已经被强噪声完全掩盖,其中高幅值随机脉冲比较明显;频谱中转频以及齿轮啮合频率谱线比较突出;在包络谱中难以辨别出故障特征频率,表明传统的谱分析方法失效。
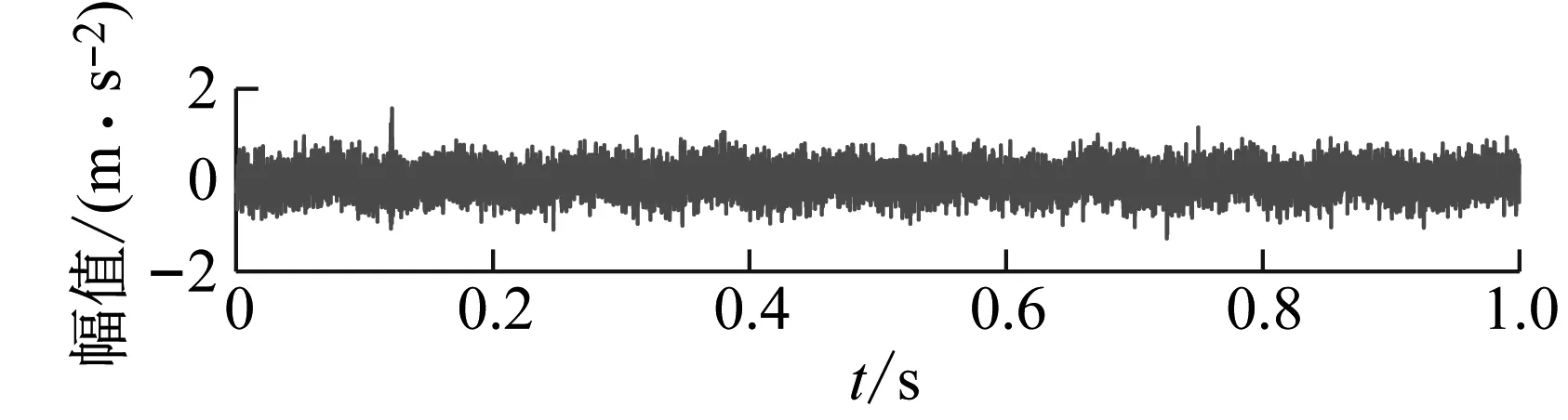
(a) 时域波形
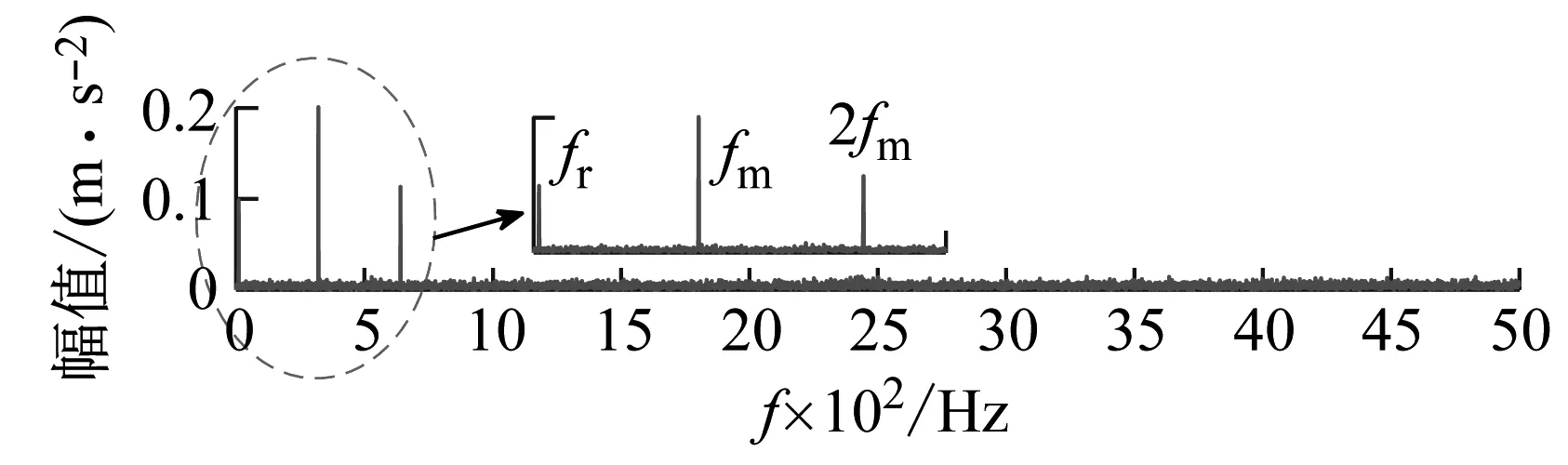
(b) 频谱
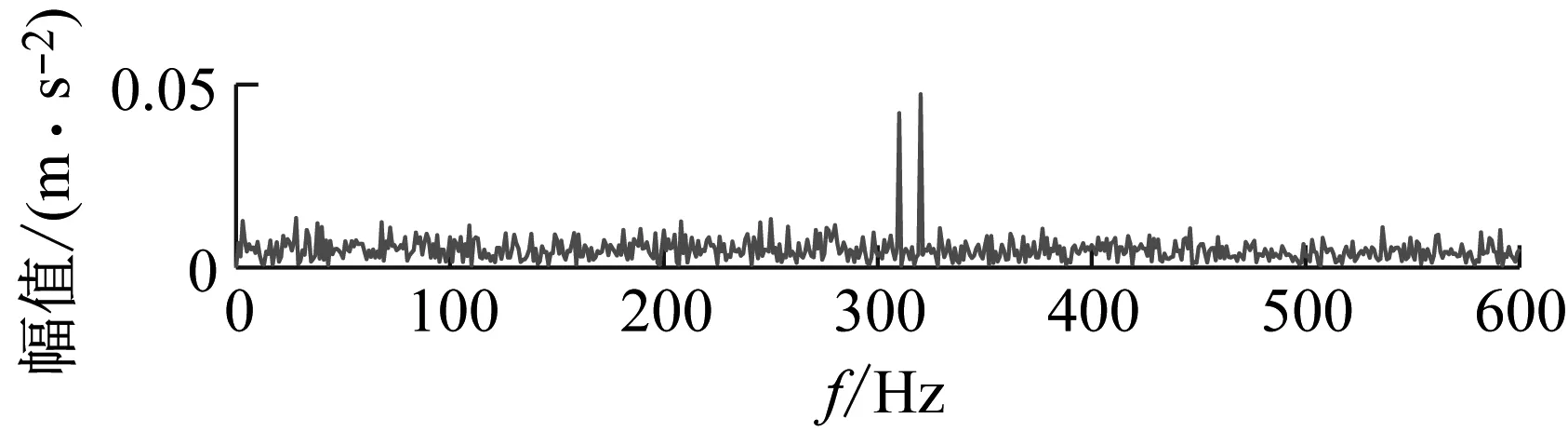
(c) 包络谱图4 仿真信号Fig.4 The simulation signal
应用本文所提方法进行分析。首先,对原始信号进行EEMD分解,生成12个IMF分量和1个余量r。计算原始信号以及各分量的包络峭度值,如图5所示,选取IMF1和IMF6进行重构,生成新的信号,其时域波形和包络谱如图6所示。可以发现,循环平稳性噪声被有效地剔除了,冲击性噪声依然存在,包络谱中可以找到故障特征频率的基频。
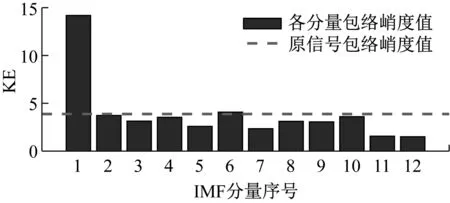
图5 各分量以及原始信号的包络峭度值Fig.5 Envelope kurtosis values of each component and original signal
(a) 时域波形
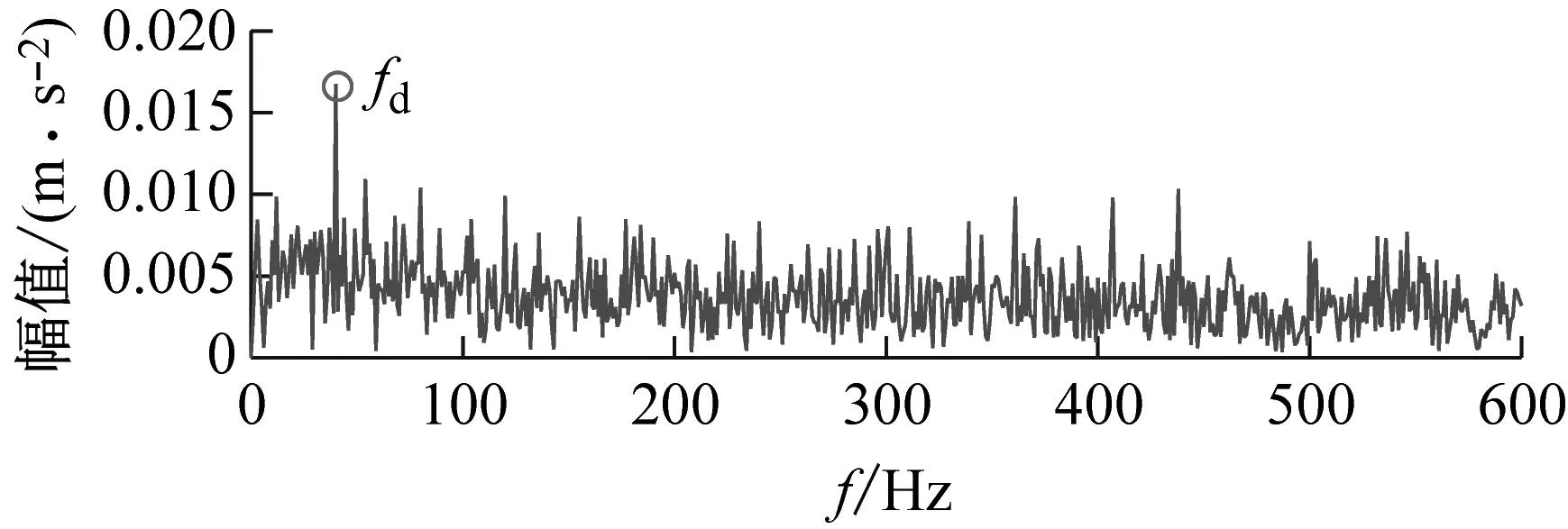
(b) 包络谱图6 新信号的时域波形以及包络谱Fig.6 The time domain waveform and envelope spectrum of the new signal
其次,以局部最大包络谱峭度为目标函数,利用PSO对VMD进行参数优化,用优化后的VMD对新信号分解,选取包络谱峭度值最大的分量进行包络解调分析,结果如图7所示。在时域波形上可以看到清晰的故障冲击,高幅值随机脉冲被有效剔除;在包络谱上可以清晰地发现故障特征频率的基频及其倍频,谱线都很突出。结果表明,本文方法可以在复杂干扰下,准确提取出轴承的故障特征信息。
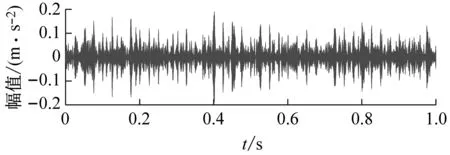
(a) 时域波形
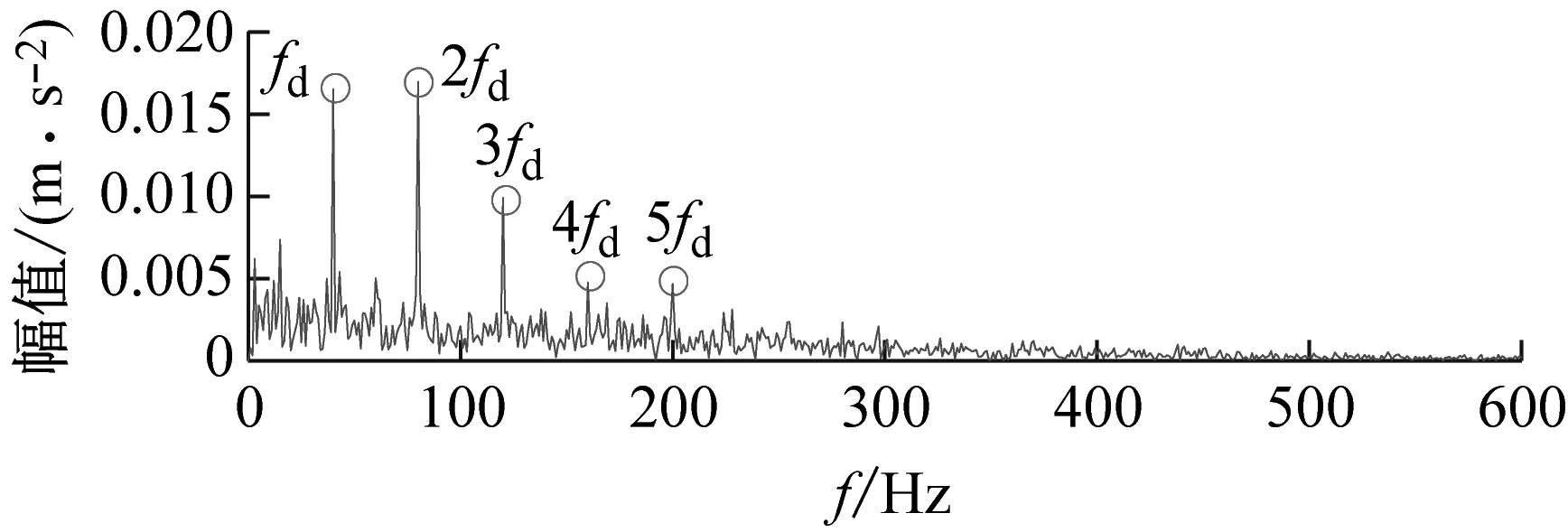
(b) 包络谱图7 本文所提方法的最终结果Fig.7 The final result of the method presented in this paper
为说明本文方法的优越性,直接对原始信号进行参数自适应VMD方法分析。以KE为评价指标,最优分量如图8所示,只能发现高幅值冲击,找不到任何故障信息;以KES为评价指标,最优分量如图9所示,搜寻到的是齿轮啮合信息。用目前提出的先进复合指标进行寻优,分别以EKI、KCI和SII为评价指标,最终分析结果如图10、图11和图12所示,由于受冲击性噪声或循环平稳性噪声的影响,这三种指标引导的参数自适应VMD方法依然不能找到轴承的故障信息。
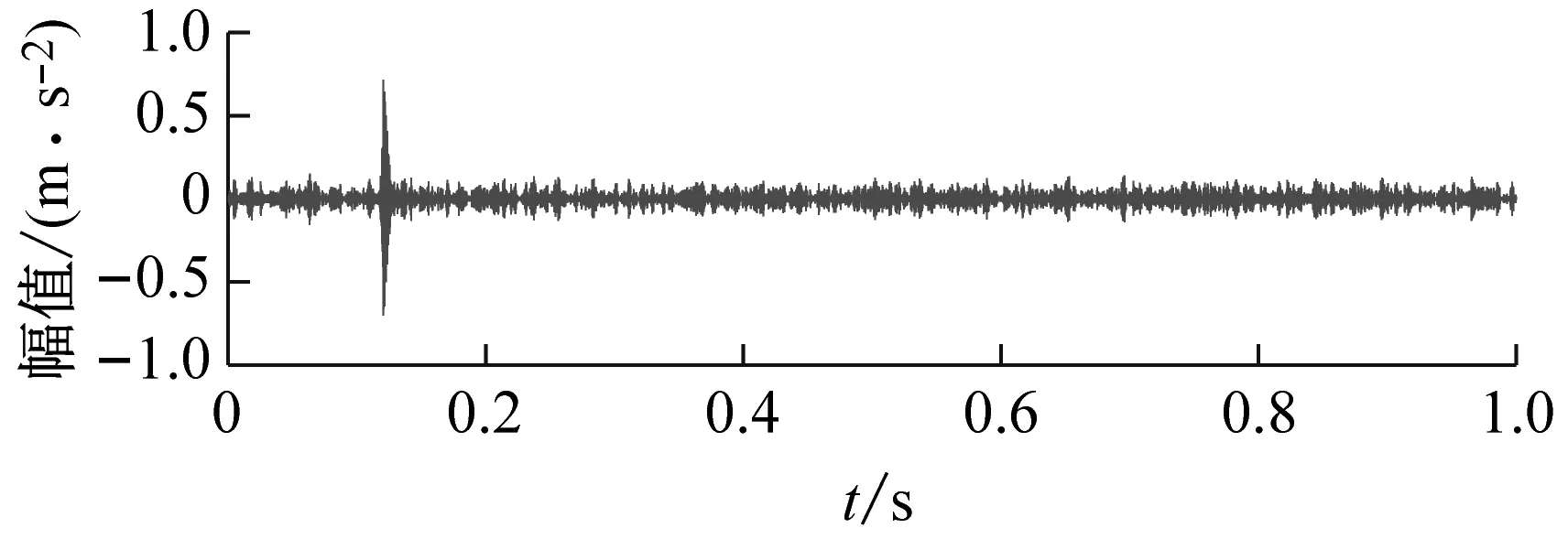
(a) 时域波形
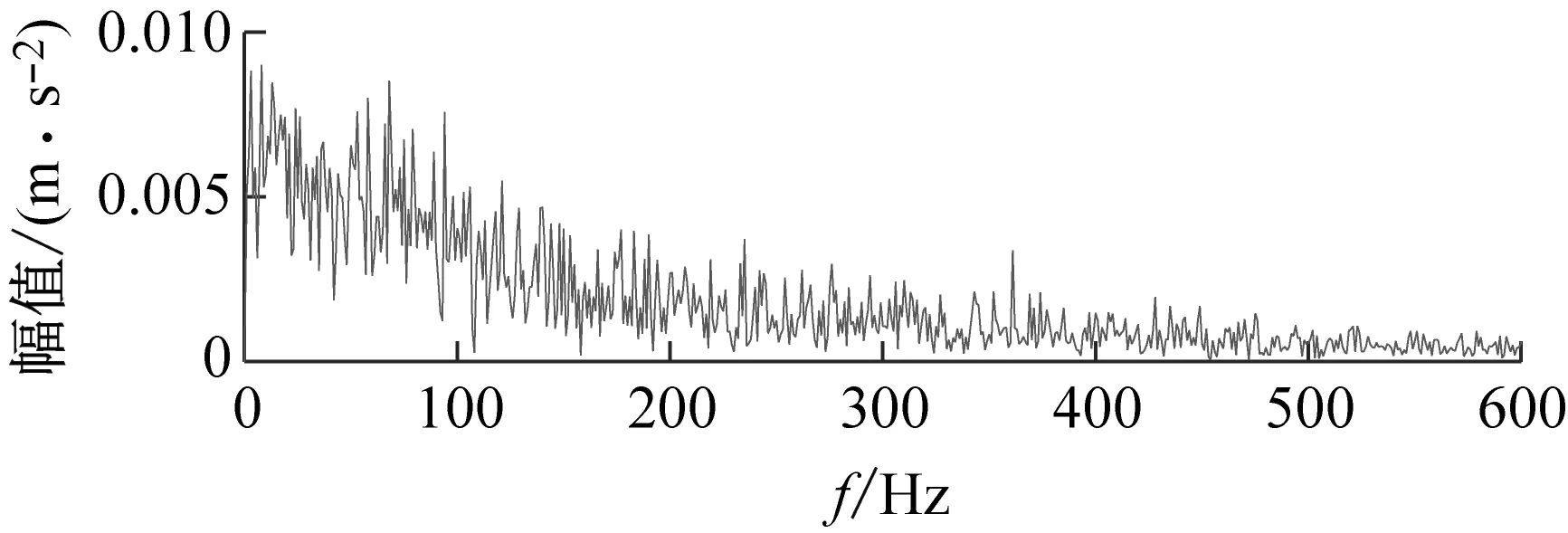
(b) 包络谱图8 以KE为目标函数的VMD分析结果Fig.8 VMD analysis results with KE as the objective function
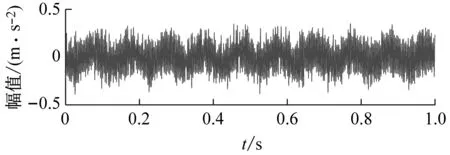
(a) 时域波形
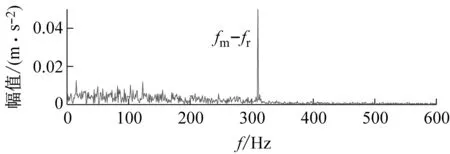
(b) 包络谱图9 以KES为目标函数的VMD分析结果Fig.9 VMD analysis results with KES as the objective function
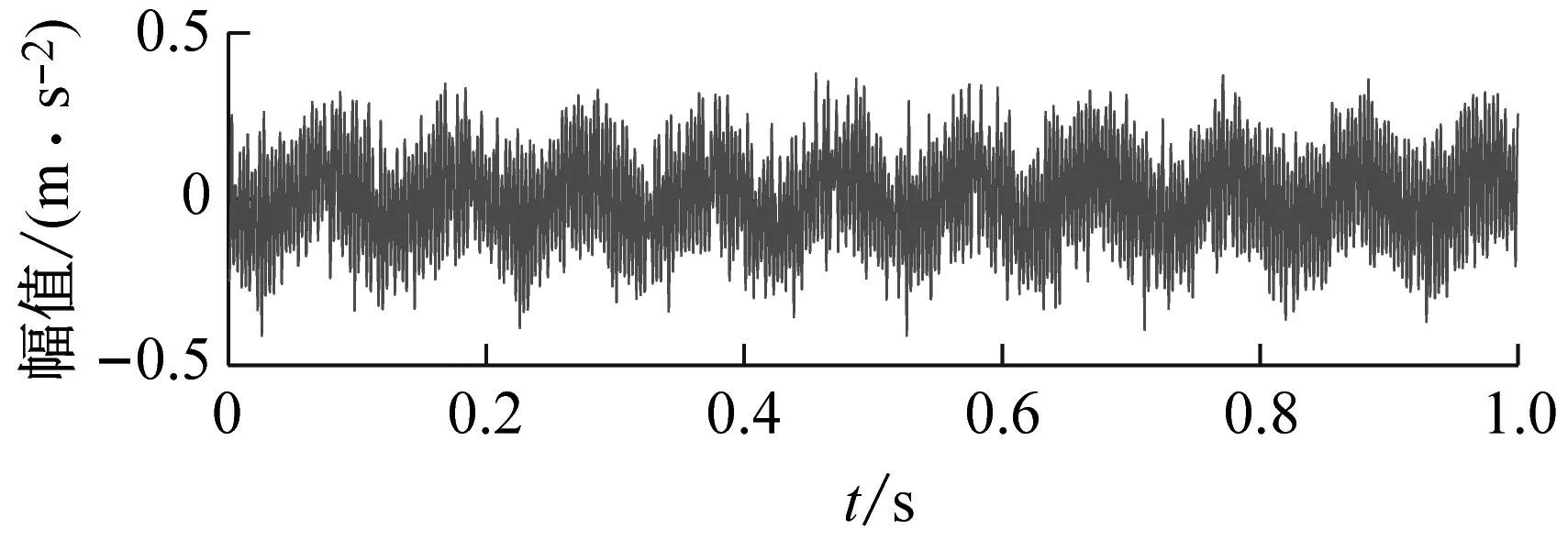
(a) 时域波形
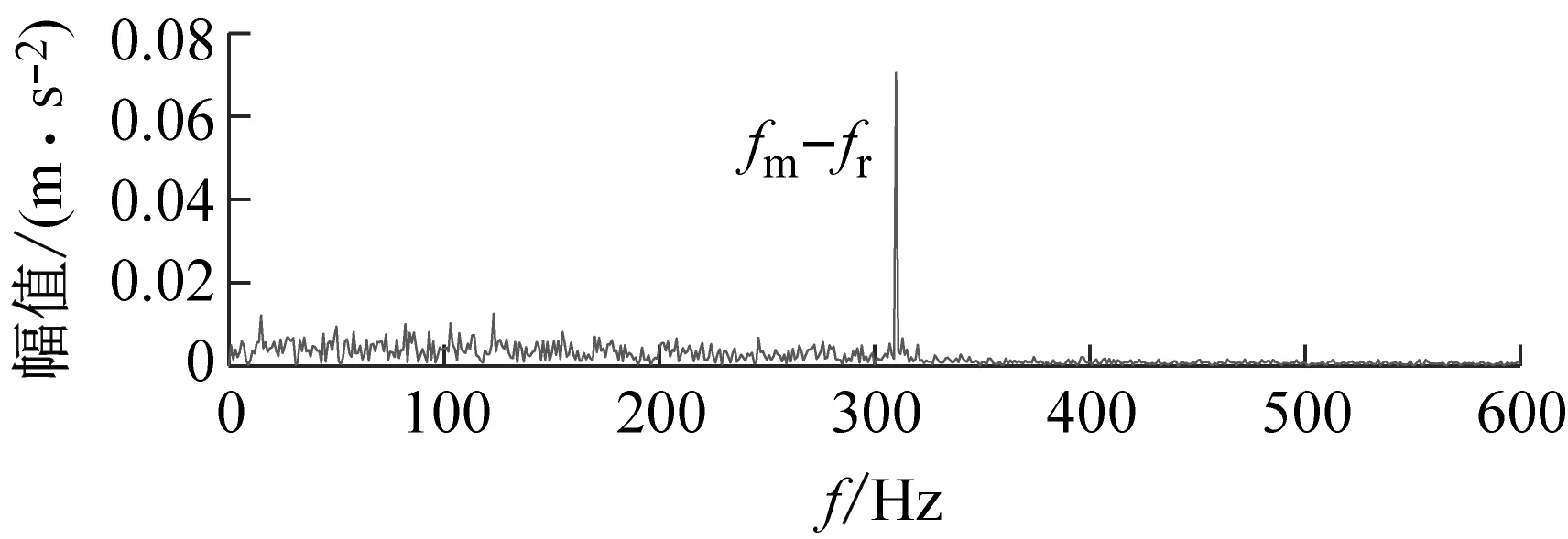
(b) 包络谱图10 以EKI为目标函数的VMD分析结果Fig.10 VMD analysis results with EKI as the objective function
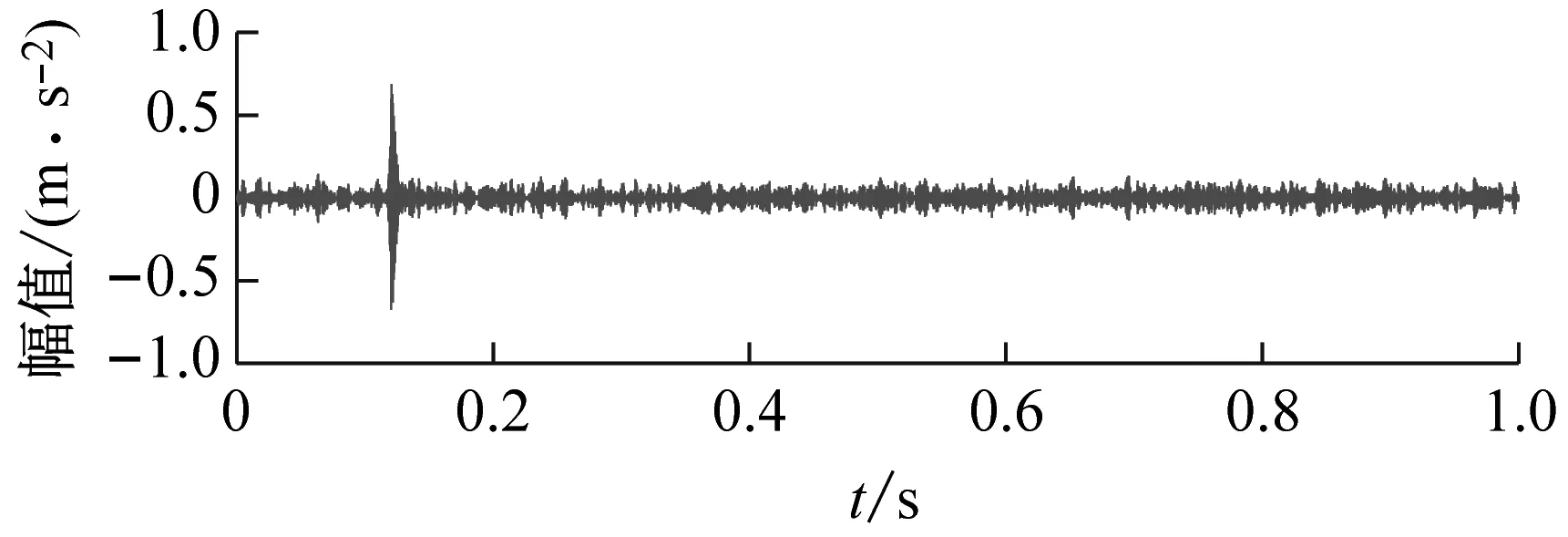
(a) 时域波形
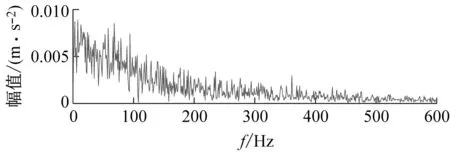
(b) 包络谱图11 以KCI为目标函数的VMD分析结果Fig.11 VMD analysis results with KCI as the objective function
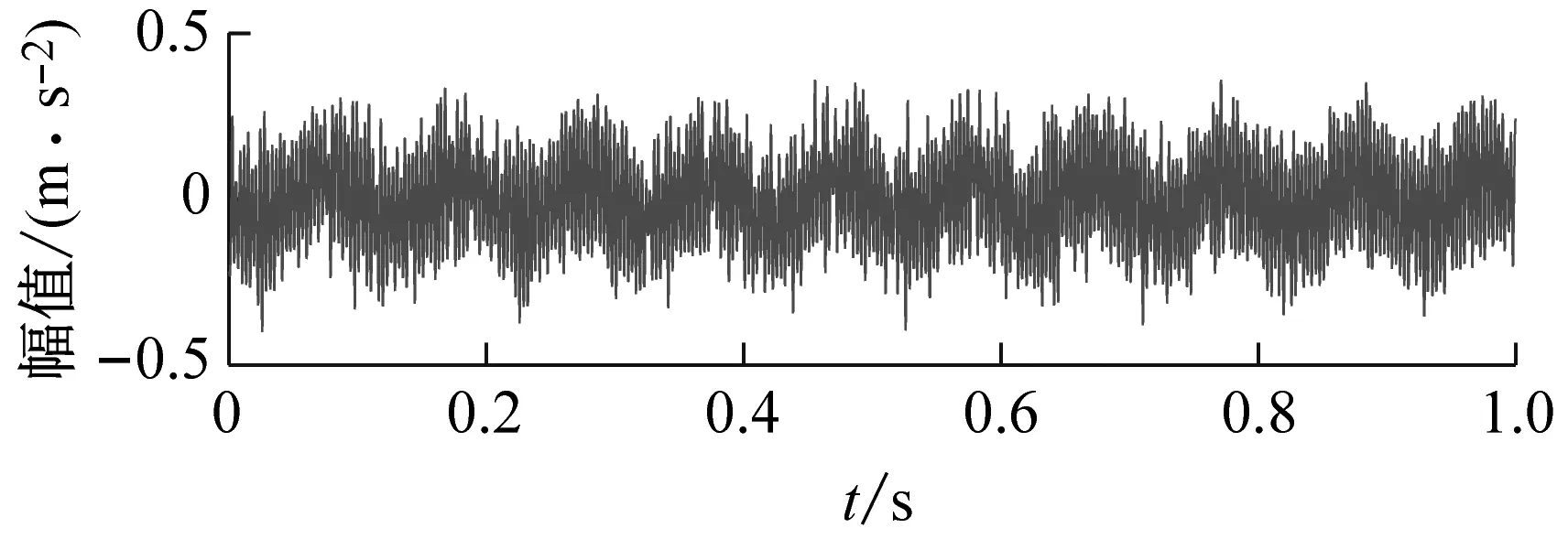
(a) 时域波形
(b) 包络谱图12 以SII为目标函数的VMD分析结果Fig.12 VMD analysis results with SII as the objective function
4 试验信号分析
为进一步验证本文所提方法的有效性,将其应用于高速列车轮对轴承的故障诊断分析。铁路轴承综合试验台以及测试轴承如图13所示。测试轴承主要结构参数如表3所示,轴承的外圈上存在长5 mm,宽1 mm,深0.7 mm的损伤。与它的几何形状相比,缺陷尺寸相对较小。

(a) 铁路轴承综合试验台
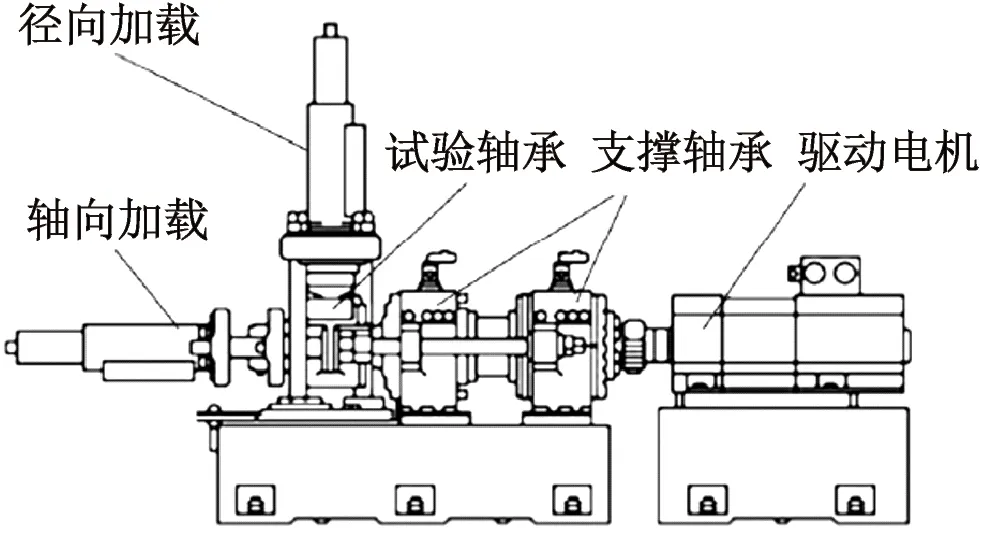
(b) 铁路轴承综合试验台结构图

(c) 测试轴承图13 铁路轴承综合试验台及故障轴承Fig.13 Railway bearing comprehensive test-bed and fault bearing

表3 测试轴承主要参数
试验时,为模拟轮对轴承真实的运行工况,施加平均径向力为80 kN,最大轴向力为±40 kN,激励频率为0.2~20 Hz的动态荷载。
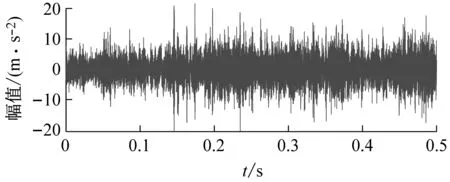
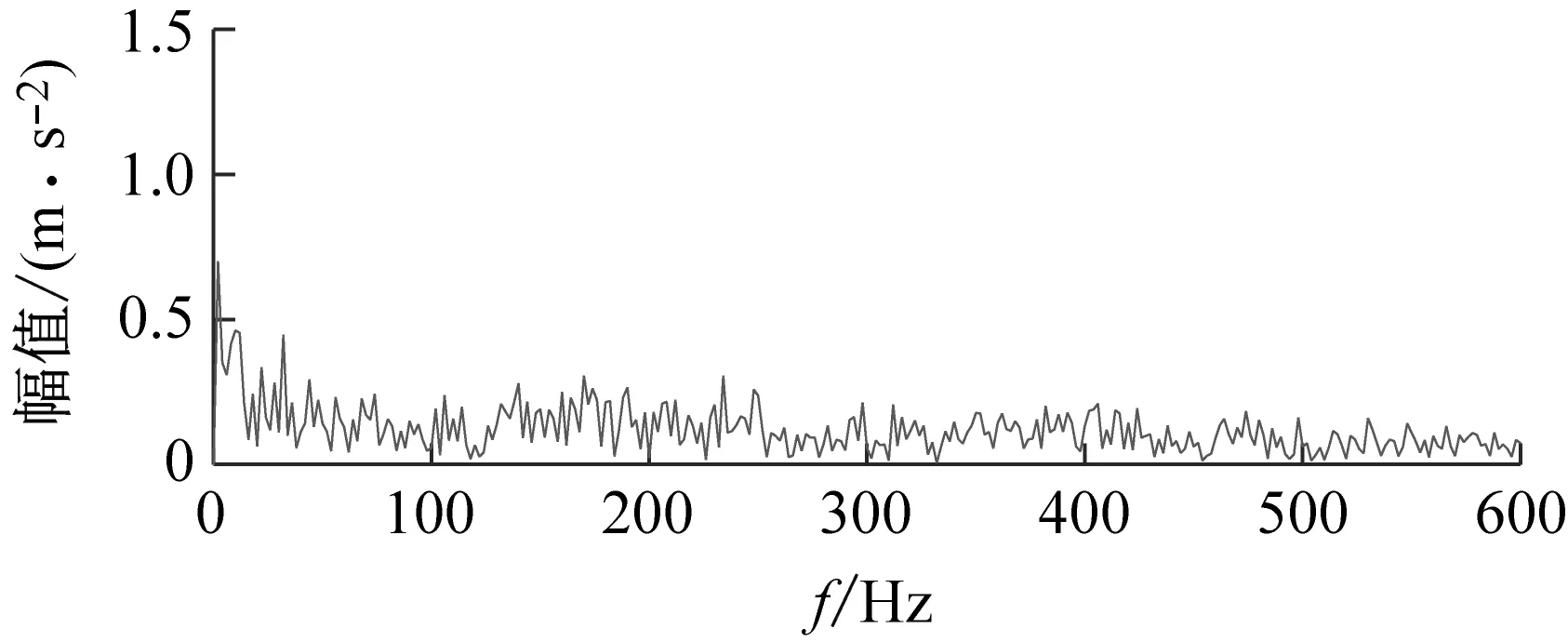
采样频率为51.2 kHz,转频为28.5 Hz。根据轴承尺寸和试验工况,计算得到外圈故障频率fBPFO=208.1 Hz。应用加速度传感器采集60 s的振动数据,截取其中0.5 s的数据进行分析,其时域波形和包络谱如图14所示。由于受到背景噪声的干扰,从时域信号中无法找到较明显的故障冲击,包络谱中亦看不到故障特征频率谱线,表明传统的谱分析方法失效。
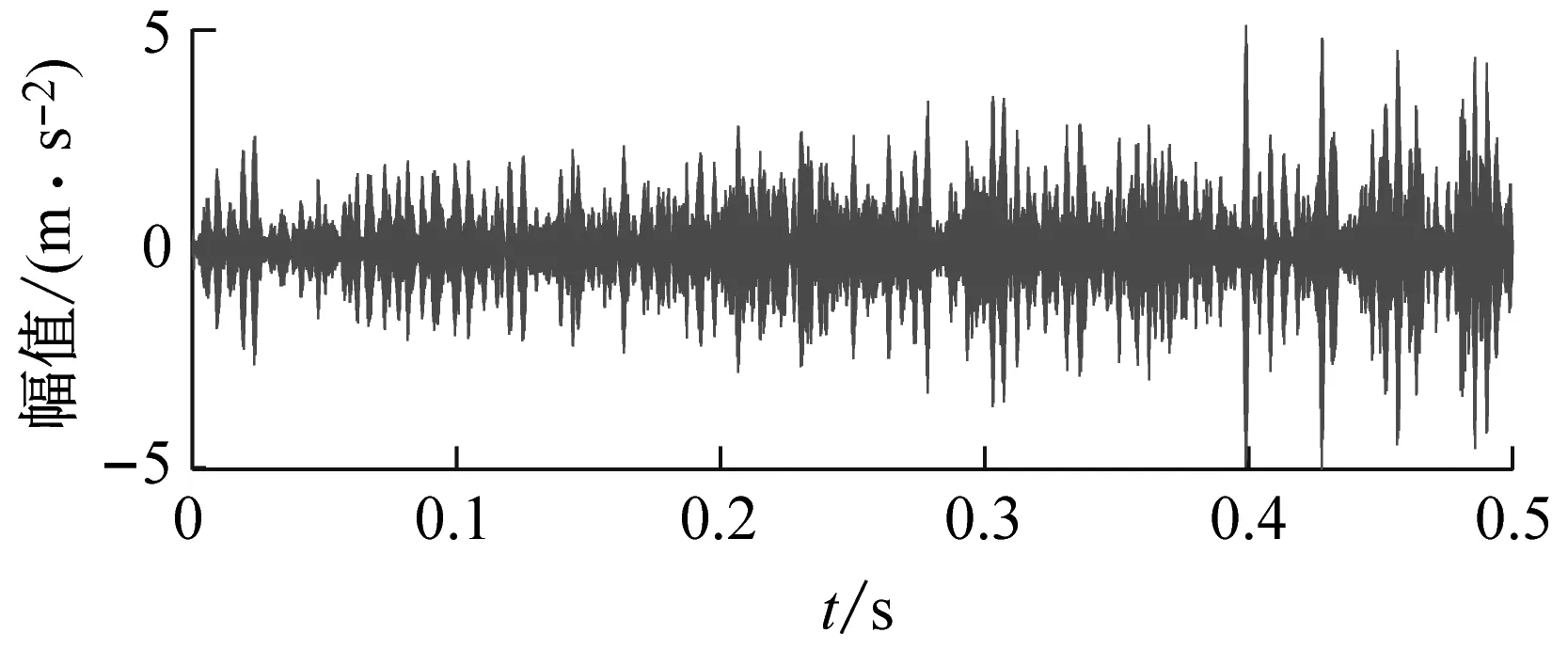
应用本文所提方法对试验数据进行分析。首先,对原始信号进行EEMD分解,生成13个IMF分量和1个余量r。计算原始信号以及各分量的包络峭度值,如图15所示,选取IMF1、IMF2、IMF4和IMF5进行重构,生成新的信号,其时域波形和包络谱如图16所示。从时域图上可以看出噪声含量有所降低,但包络谱上依然找不到故障特征频率的谱线。
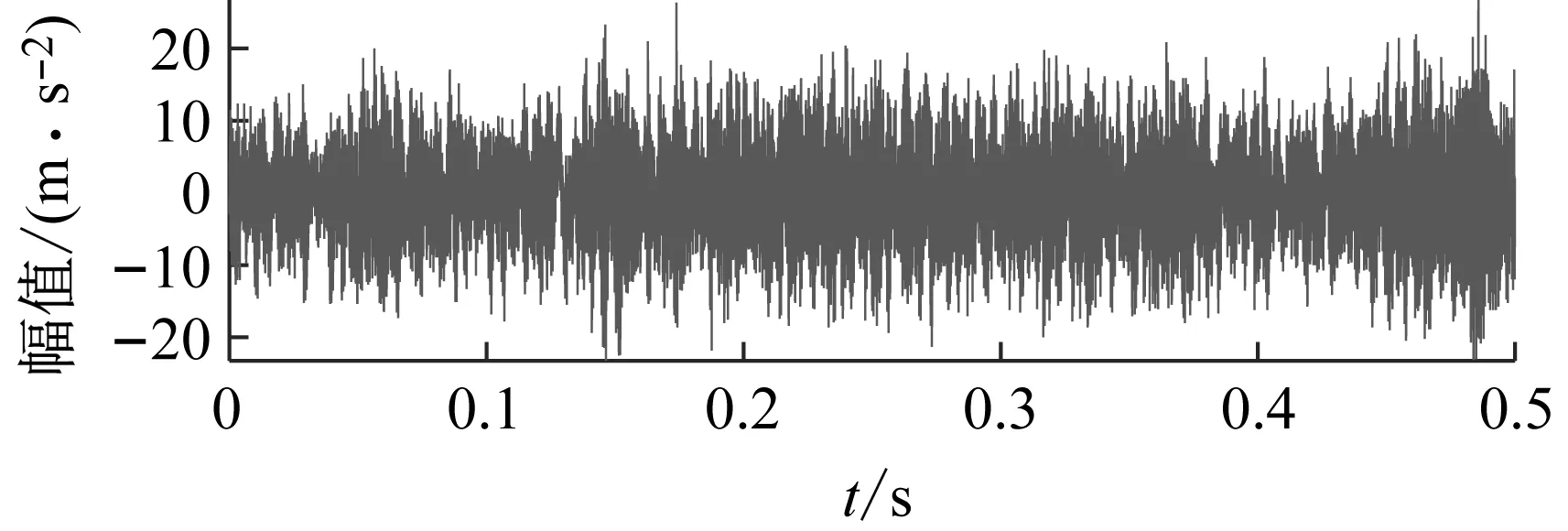
(a) 时域波形
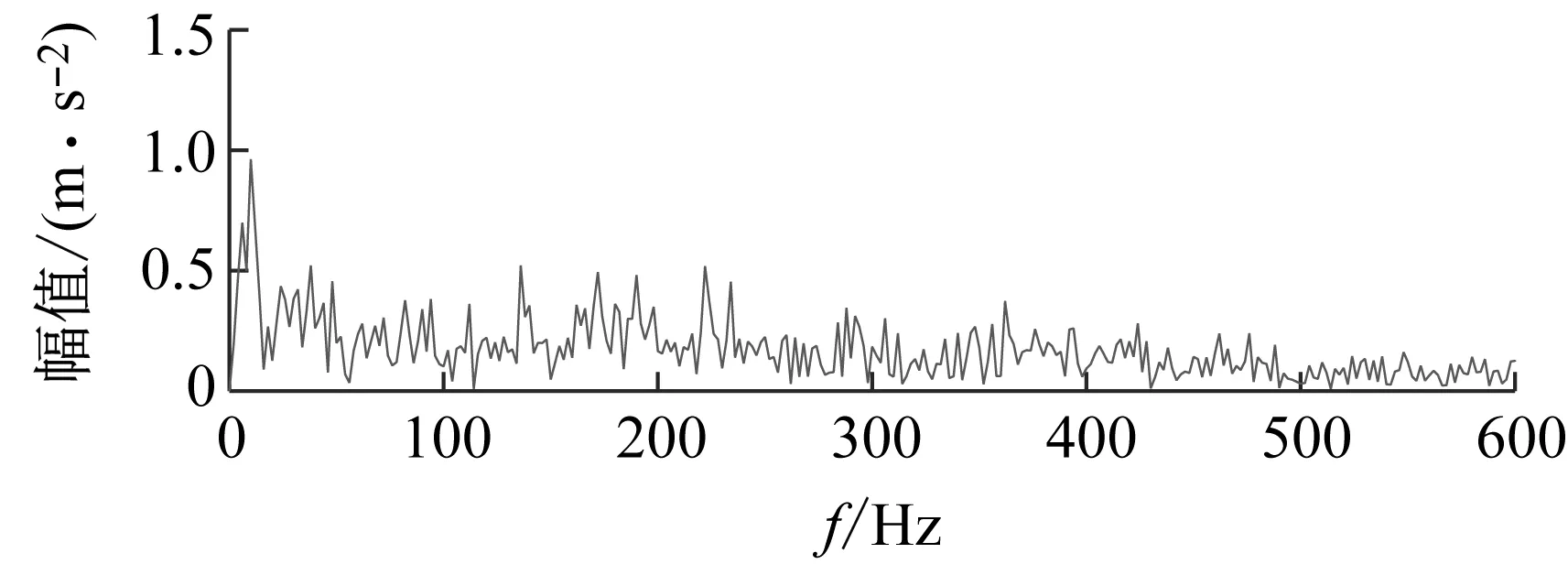
(b) 包络谱图14 试验信号Fig.14 Test signal
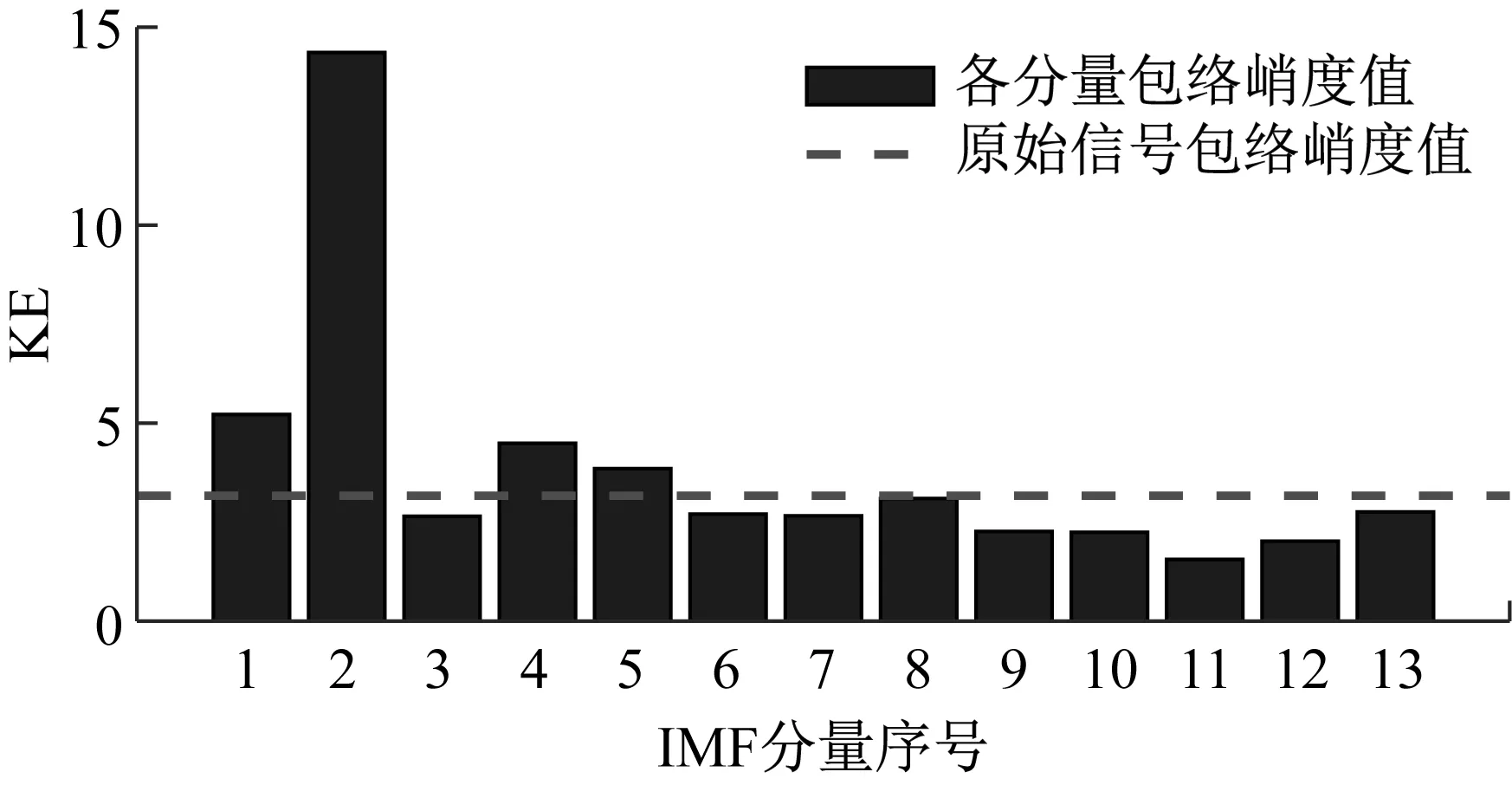
图15 各分量以及原始信号的包络峭度值Fig.15 Envelope kurtosis values of each component and original signal
(a) 时域波形
(b) 包络谱图16 新信号的时域波形以及包络谱Fig.16 The time domain waveform and envelope spectrum of the new signal
其次,以局部最大包络谱峭度为目标函数,利用PSO对VMD进行参数优化,用优化后的VMD对新信号分解,选取包络谱峭度值最大的分量进行包络解调分析,结果如图17所示。在时域波形上可以看到清晰的故障冲击;在包络谱上可以清晰地发现故障特征频率的基频及其二倍频,谱线都很突出。结果表明,本文方法可以在复杂干扰下,准确提取出轮对轴承的故障特征信息。
(a) 时域波形
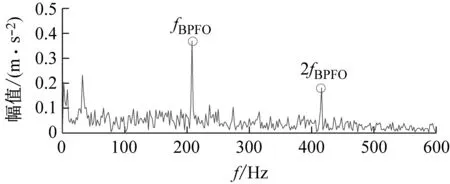
(b) 包络谱图17 本文所提方法的最终结果Fig.17 The final result of the method presented in this paper
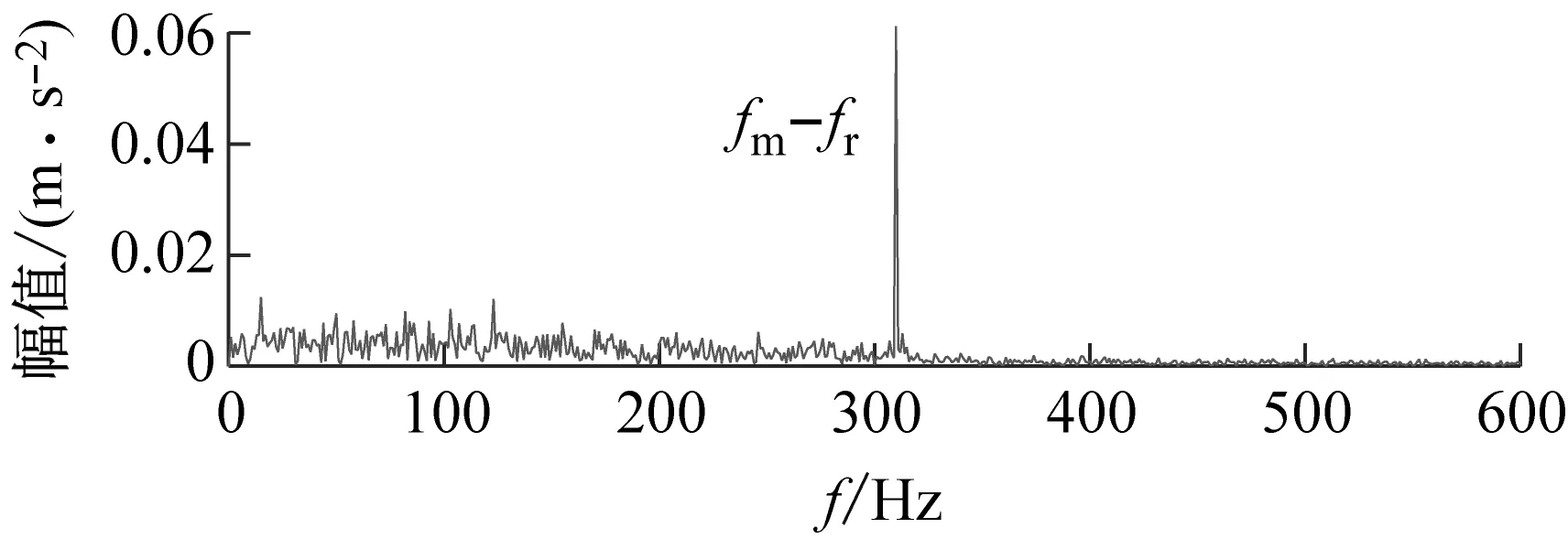
为说明本文方法的优越性,直接对原始信号进行参数自适应VMD方法分析。以KE为评价指标,最优分量如图18所示,时域波形上有高幅值冲击,包络谱上找不到任何外圈故障信息;以KES为评价指标,最优分量如图19所示,包络谱上亦发现不了外圈故障信息。用目前提出的先进复合指标进行寻优,分别以EKI、KCI和SII为评价指标,最终分析结果如图20、图21和图22所示,由于受到强噪声的干扰,这三种指标引导的VMD依然不能找到外圈的故障信息。
(a) 时域波形
(b) 包络谱图18 以KE为目标函数的VMD分析结果Fig.18 VMD analysis results with KE as the objective function
(a) 时域波形
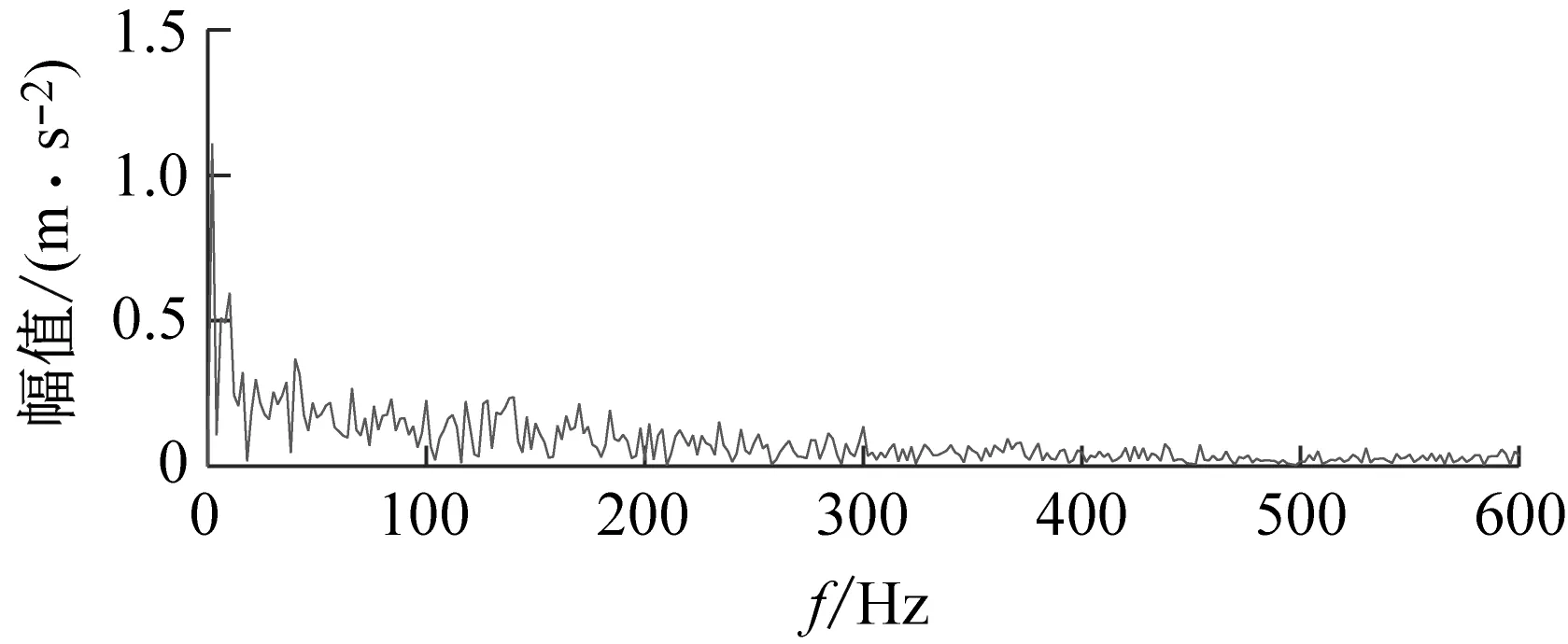
(b) 包络谱图19 以KES为目标函数的VMD分析结果Fig.19 VMD analysis results with KES as the objective function
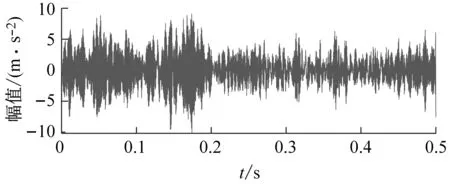
(a) 时域波形
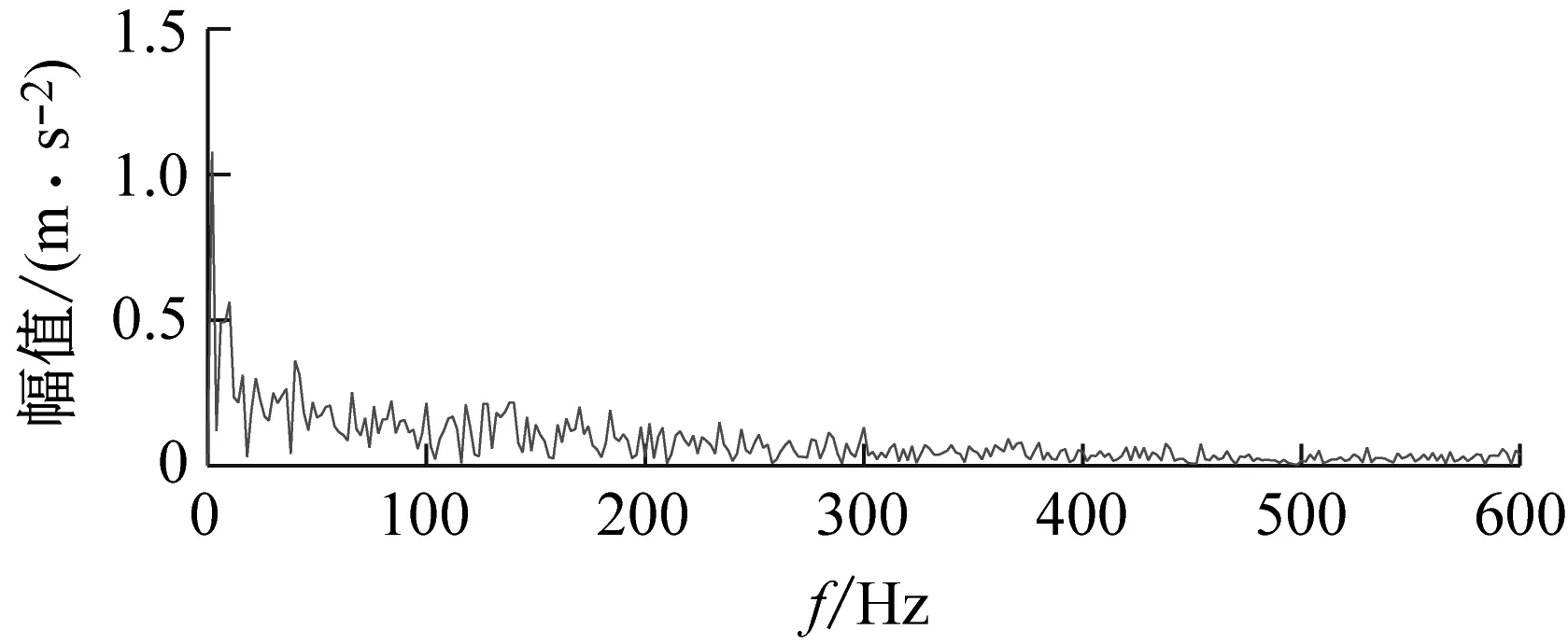
(b) 包络谱图20 以EKI为目标函数的VMD分析结果Fig.20 VMD analysis results with EKI as the objective function
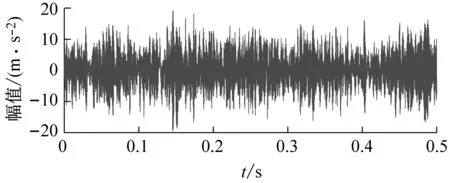
(a) 时域波形
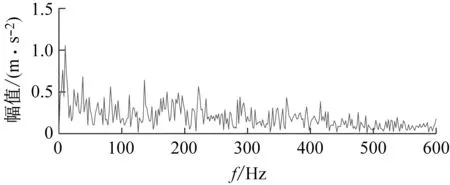
(b) 包络谱图21 以KCI为目标函数的VMD分析结果Fig.21 VMD analysis results with KCI as the objective function
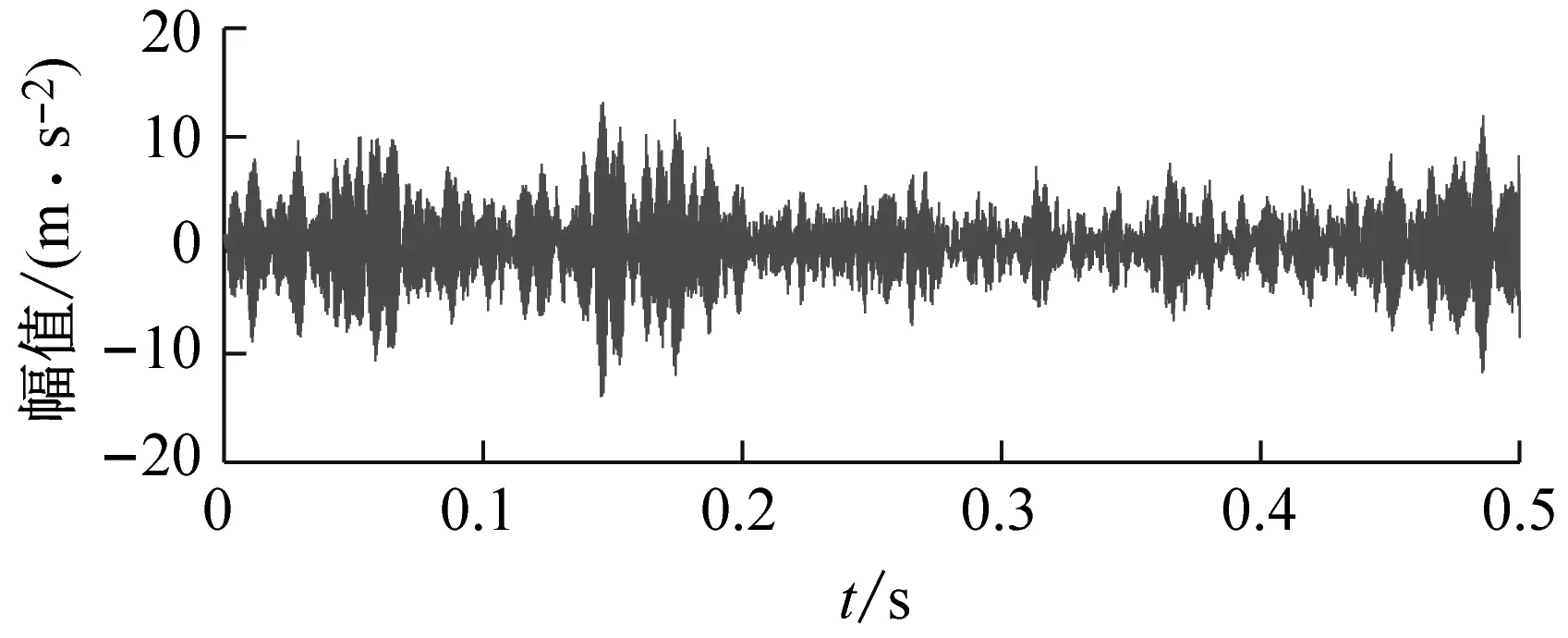
(a) 时域波形
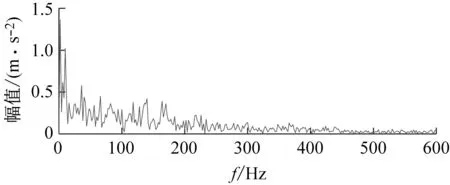
(b) 包络谱图22 以SII为目标函数的VMD分析结果Fig.22 VMD analysis results with SII as the objective function
5 结 论
(1) 本文在文献[21]使用的粒子群基础上,将凹函数递减权值代替线性递减权值,进一步提升了PSO的全局搜索能力。
(2) VMD能够将信号在频域内进行精细分析,但效果受到K和α的影响。利用智能优化算法可自适应确定这两个关键参数,但优化效果严重依赖于目标函数。在强噪声干扰下,现有作为目标函数的故障评价指标又易受冲击性噪声或循环平稳性噪声的影响。
(3) 针对传统参数自适应VMD方法易受噪声影响的问题,提出了基于EEMD预处理的参数自适应VMD方法。首先信号经EEMD分解,以包络峭度为指标,可以消除循环平稳性噪声的影响。其次利用VMD优秀的故障特征提取能力,以包络谱峭度为指标可以避开冲击性噪声的影响。通过仿真和试验分析,验证了本文所提方法的有效性和鲁棒性。结果表明,该种方法在强干扰环境下依然能够实现轮对轴承故障的精准诊断,效果优于传统参数自适应VMD方法。
