约束膜式空气弹簧的刚度建模与分析
2022-01-27赵亚敏崔俊宁邹丽敏边星元程钟义
赵亚敏, 崔俊宁, 邹丽敏, 边星元 , 程钟义
(1.哈尔滨工业大学 超精密光电仪器工程研究所,哈尔滨 150080;2.哈尔滨工业大学 超精密仪器技术及智能化工信部重点实验室,哈尔滨 150080)
环境中的低频微幅振动干扰逐渐成为限制各种大型精密/超精密仪器、尖端实验系统性能的关键因素。例如,其会影响生物医学显微成像分辨力与成像质量[1]、移相干涉仪测量精度[2]、光刻机最小线宽与套刻精度[3]、卫星相机调心精度与成像质量[4]。此外,随精度与性能需求的提升,大口径天文望远镜、长焦距透镜等大型光学系统的体积、重量及结构复杂度愈发增大,不仅要求隔振设备具有高隔振性能,还提出了大承载需求。因此,开发大承载、低刚度及超低频隔振性能(<1 Hz)兼顾的高性能隔振器需求迫切[5]。
空气弹簧因其承载大、固有频率低等优点,广泛应用于大型超精密加工设备[6-8]、测量系统[9-11]的隔振领域。空气弹簧大承载、低刚度及超低频隔振性能的实现依赖于指导结构优化设计与精密加工的理论模型。郭荣生[12]假设弹性膜总弧长保持不变及弹性膜变形不引起腔室体积变化,建立了空气弹簧的刚度模型。该模型被列入隔振设计规范[13],并沿用至今[14-15]。朱德库等[16-18]建立了不同形式空气弹簧的改进刚度模型。改进模型考虑了弹性膜变形引起的腔室体积变化,但仍假设弹性膜总弧长保持不变。夏超[19]考虑弹性膜弧长变化建立了约束膜式空气弹簧的改进刚度模型,但改进模型忽略了弹性膜变形引起的腔室体积变化。空气弹簧的结构变形及压力变化必然导致弹性膜弧长发生变化,弧长的改变及其变形引起的腔室体积变化直接影响有效面积及腔室体积,进而导致实际刚度与理论值相差较大。对于由多个空气弹簧并联支撑的大型、超大型精密隔微振平台,累计误差将更加突出。
本文兼顾弹性膜弧长变化及其变形引起的腔室体积变化,建立约束膜式空气弹簧的改进刚度模型。基于改进刚度模型研究几何结构与材料参数对刚度的影响规律,实现大承载、低刚度隔振性能的优化设计。
1 理论建模
空气弹簧是一种在弹性膜中充入压缩气体,利用气体的可压缩性实现弹性支撑的非金属弹簧。由图1所示的受力分析可得
F=(P-Pa)S
(1)
(2)
式中:F为负载;S为有效面积,指载荷与腔室内部充气压强相平衡时的断面面积,或者说是弹性膜在载荷方向没有分力的断面面积,即通过弹性膜断面自由圆弧做切面时的断面面积;K为刚度;P、V为任意位置压缩气体的绝对压强及腔室体积;Pa为大气压强;P0、V0、S0为静平衡位置压缩气体的绝对压强、腔室体积及有效面积;m为气体多变指数,与运动速度有关;对于振幅几至几十μm/s的空气弹簧,m取1;dV/dx为有效体积变化率;dS/dx为有效面积变化率。空气弹簧的刚度与静平衡位置的充气压强、腔室体积、有效体积变化率、有效面积变化率有关,且有效体积变化率与有效面积变化率是刚度计算的关键参数。
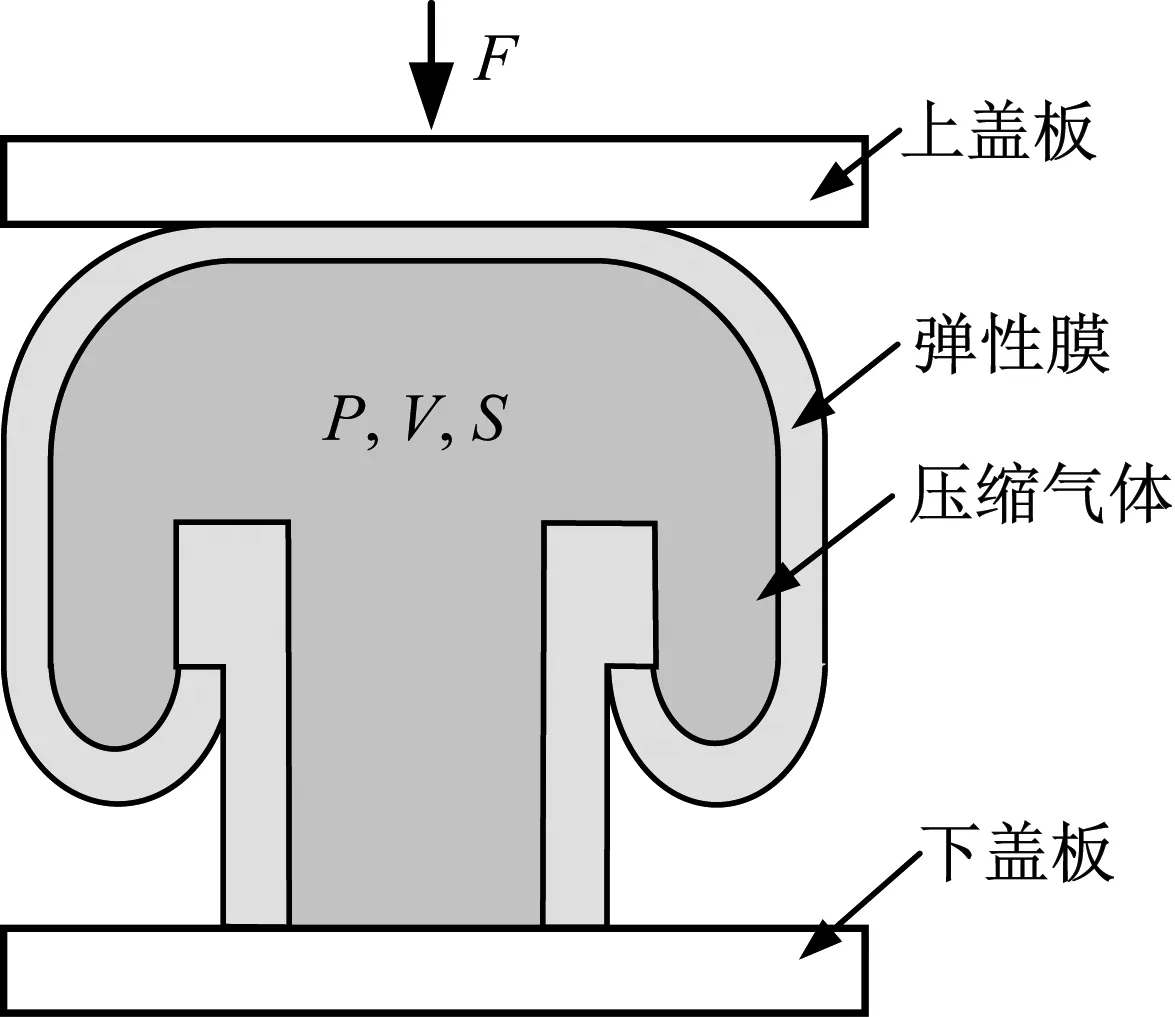
图1 受力分析图Fig.1 Stress diagram
1.1 有效面积变化率
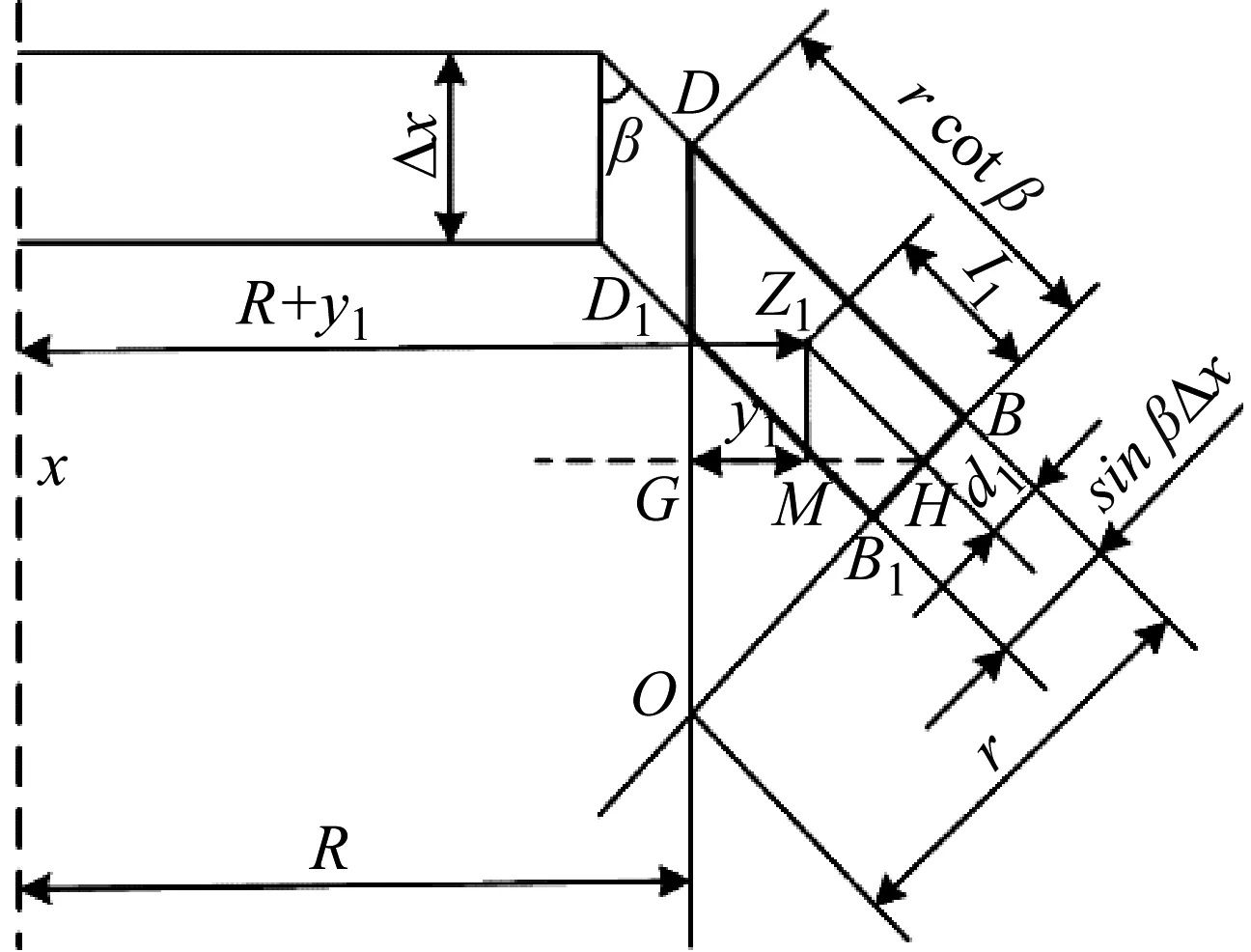
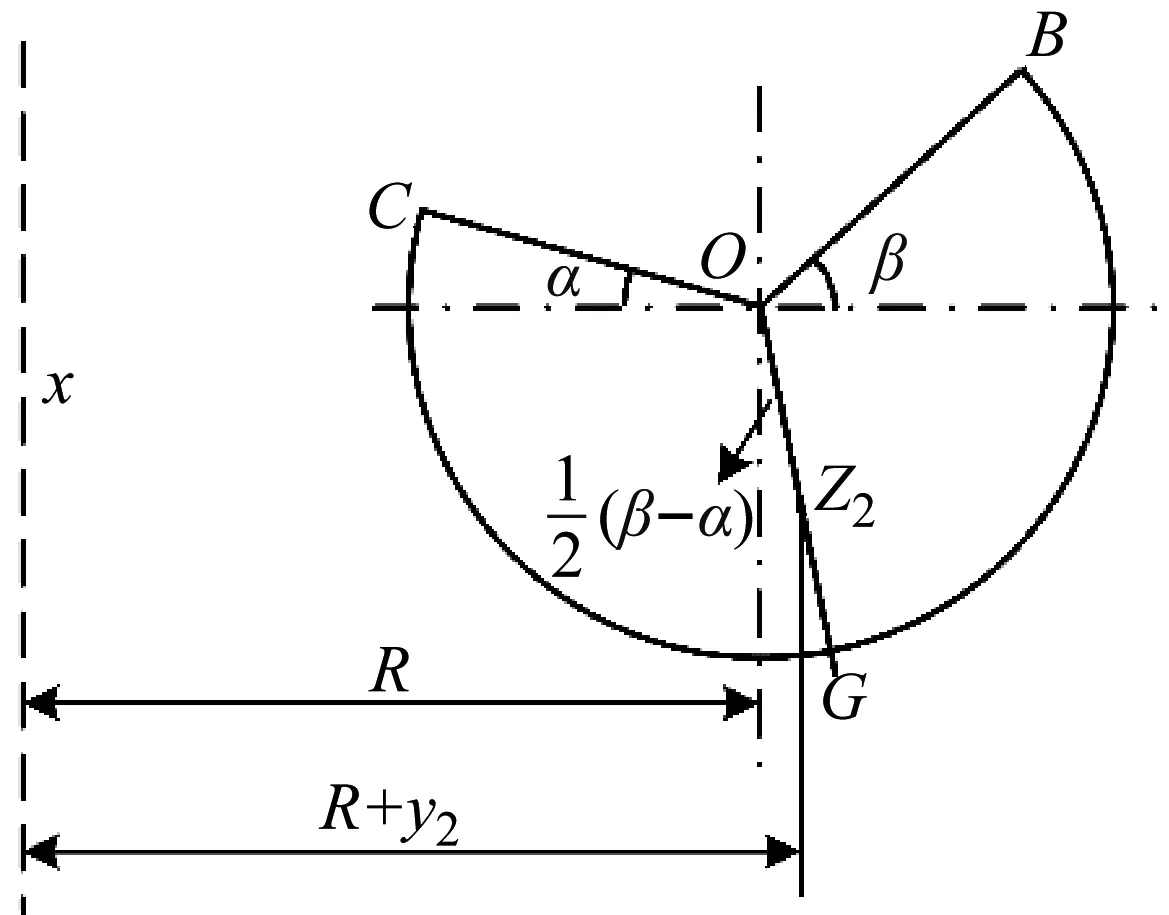
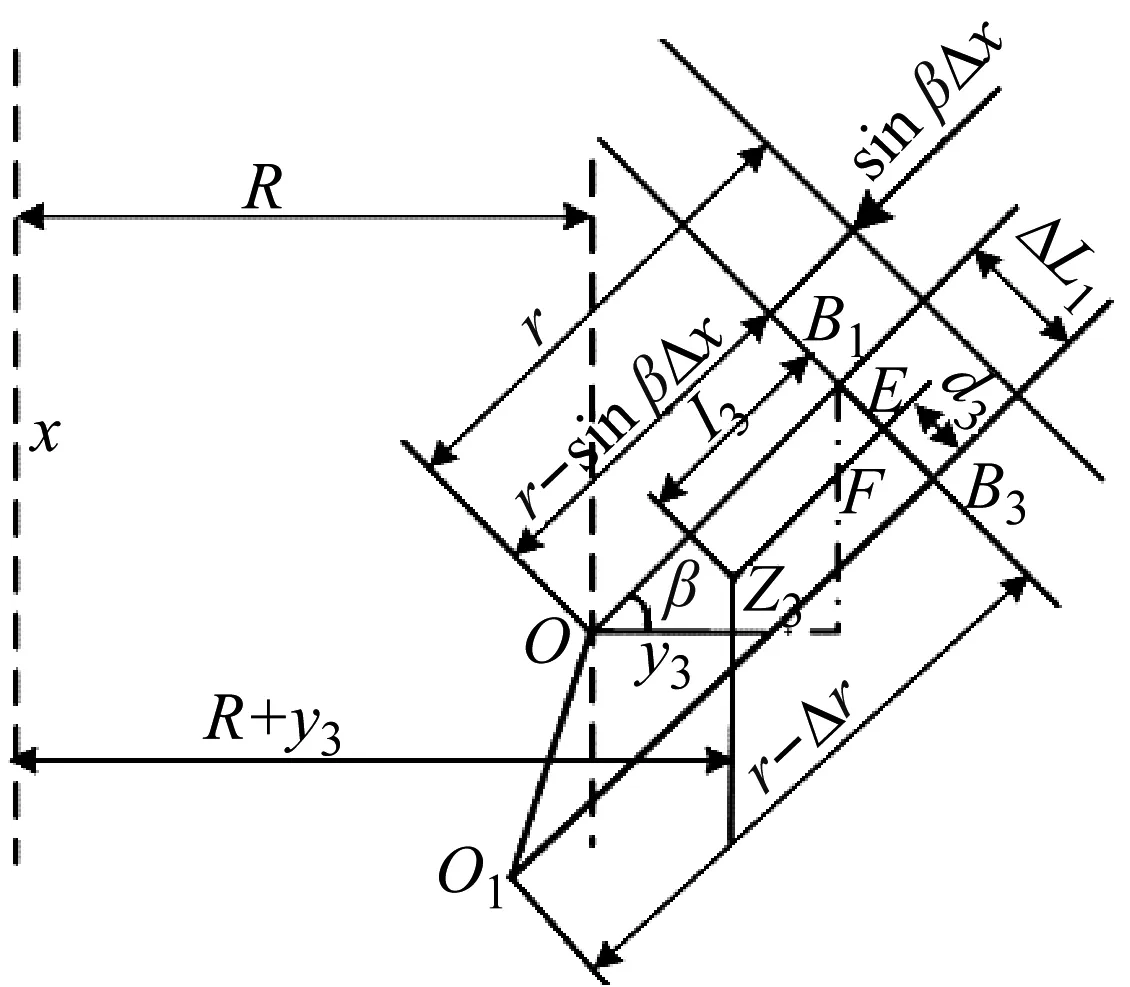
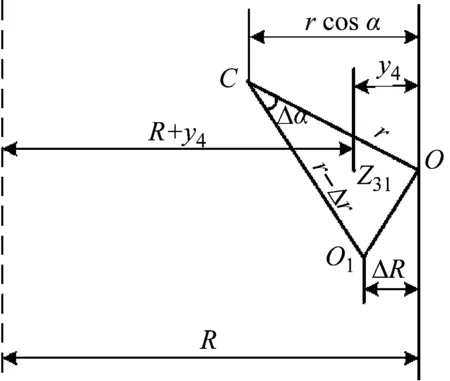
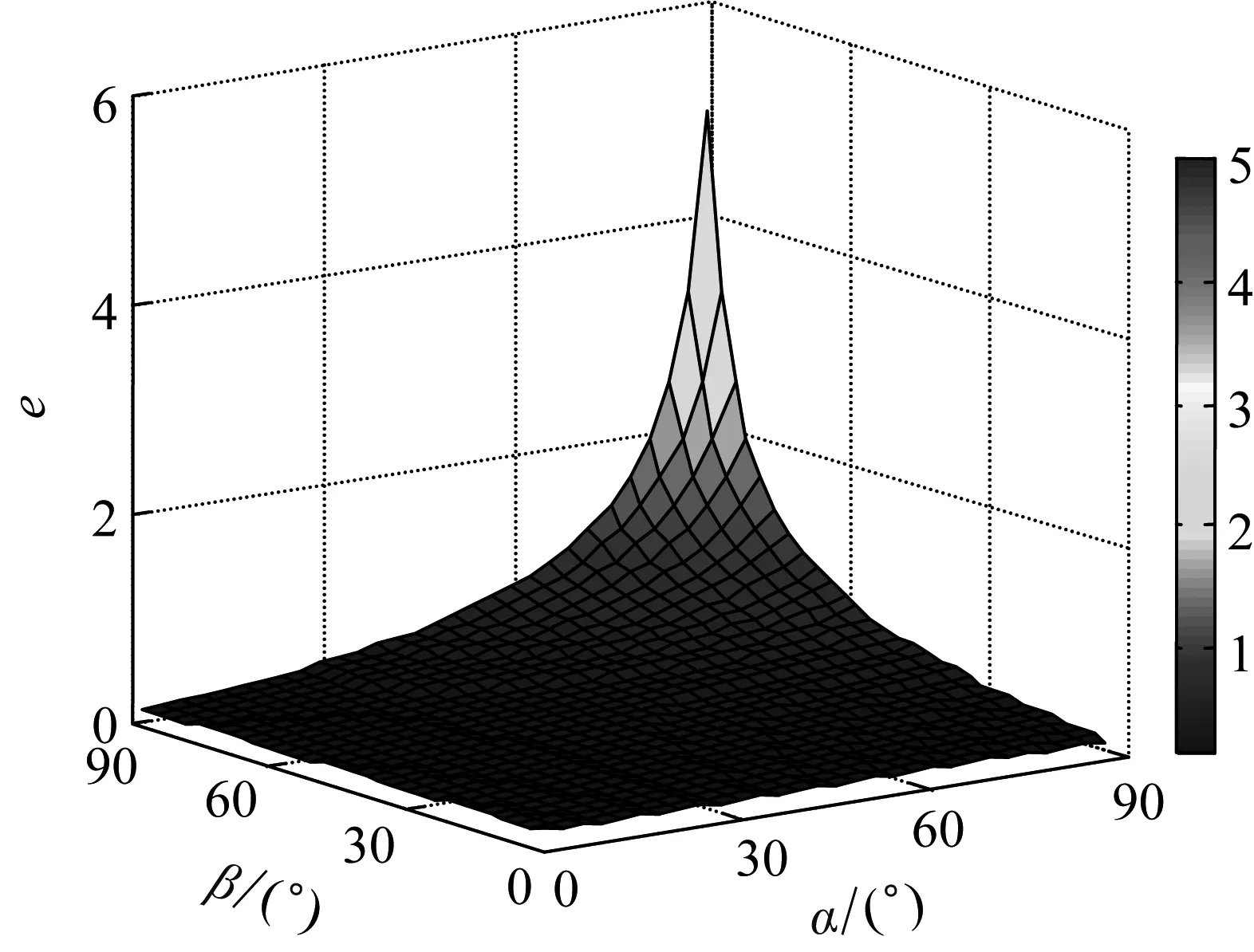
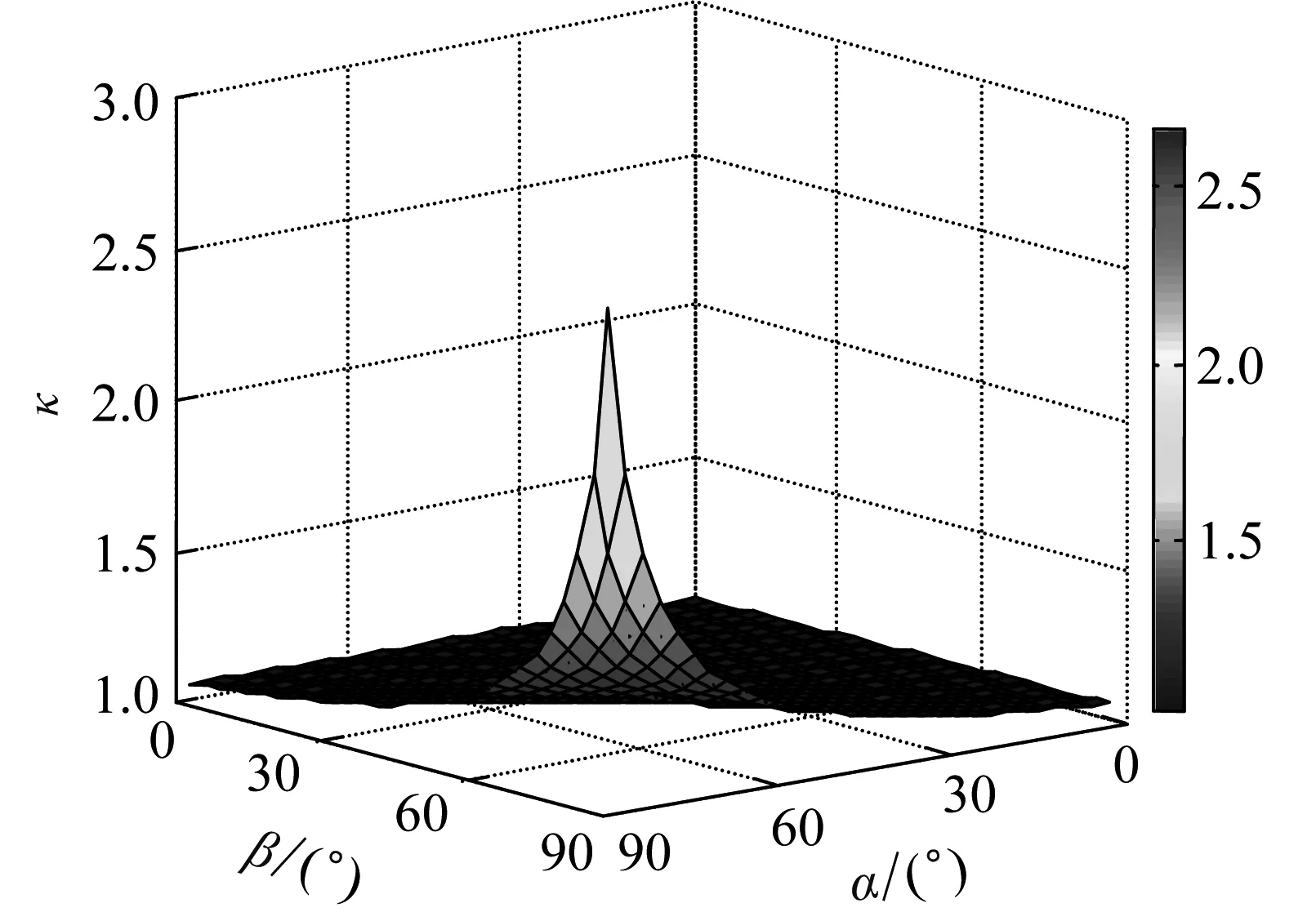
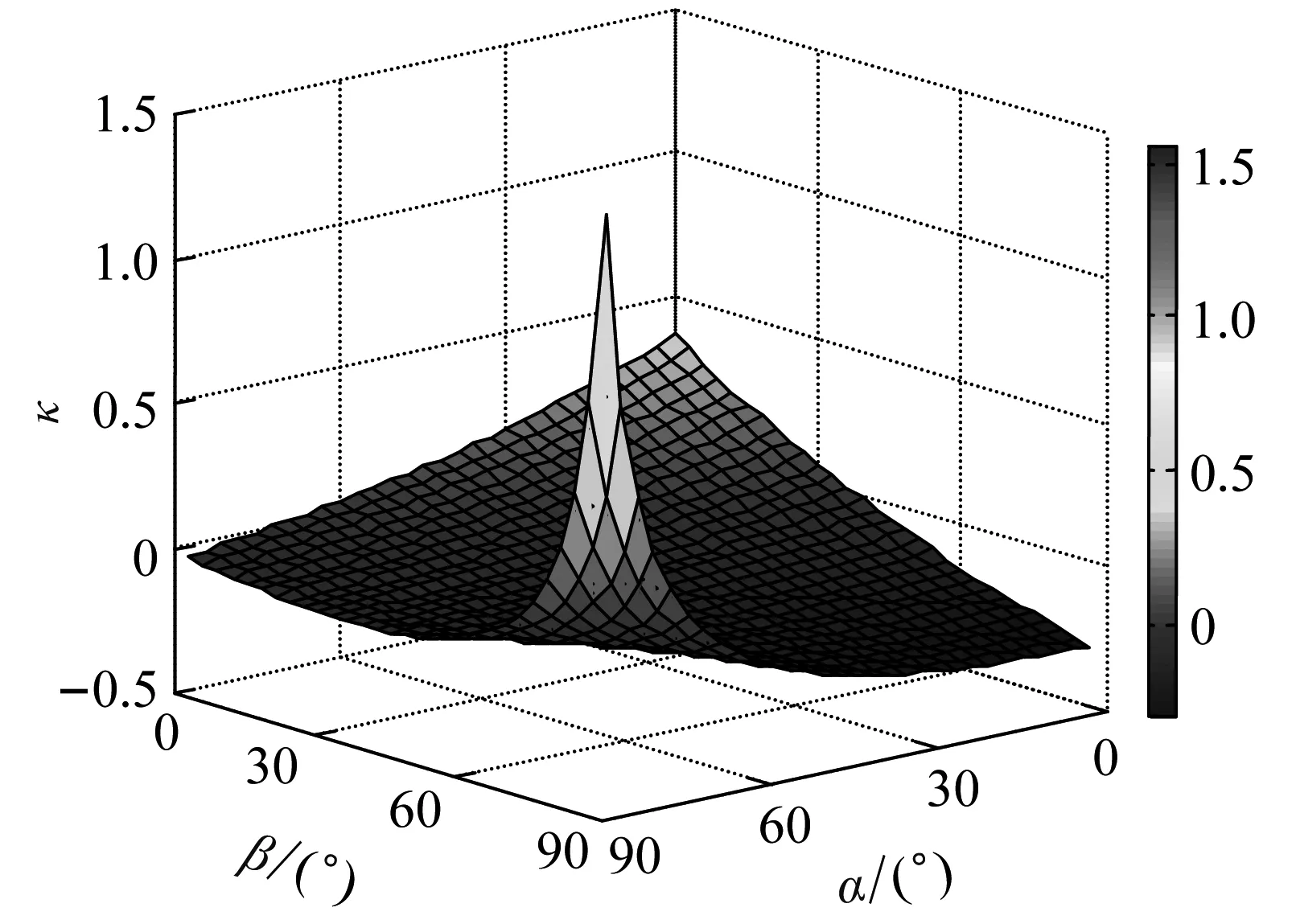
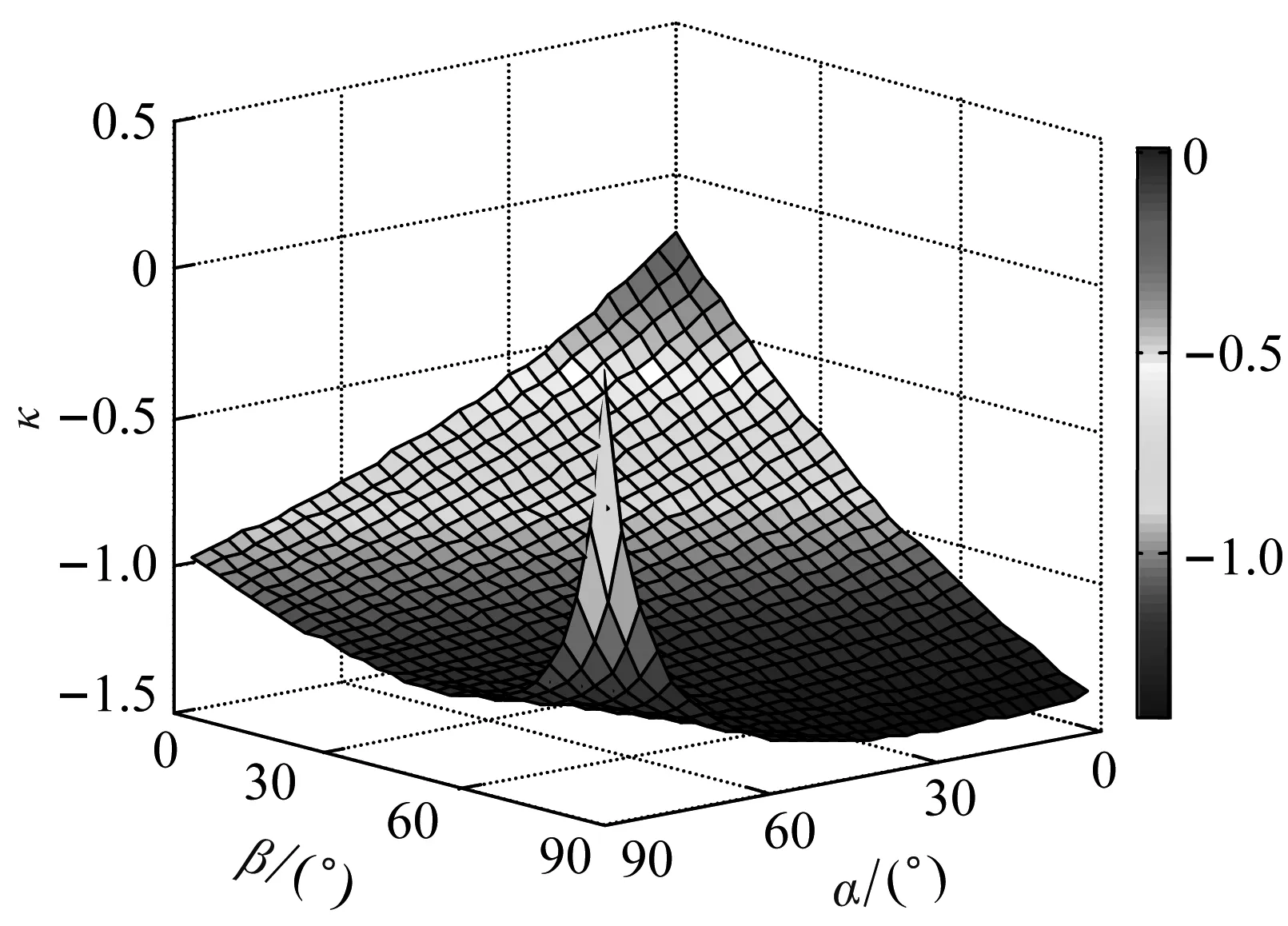
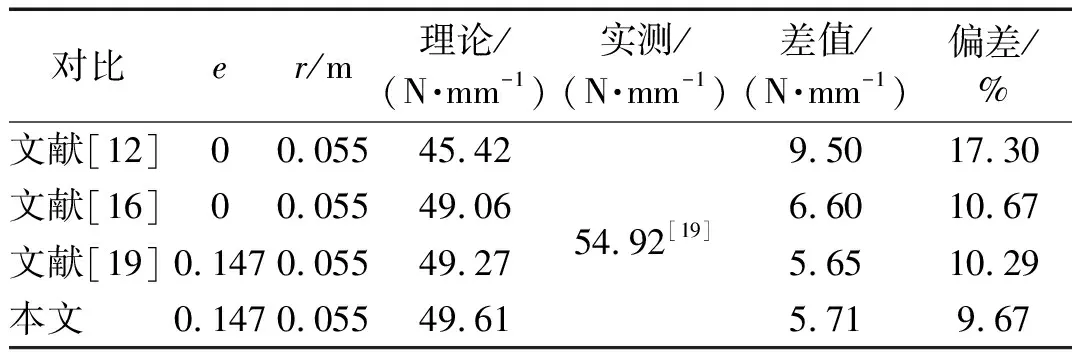
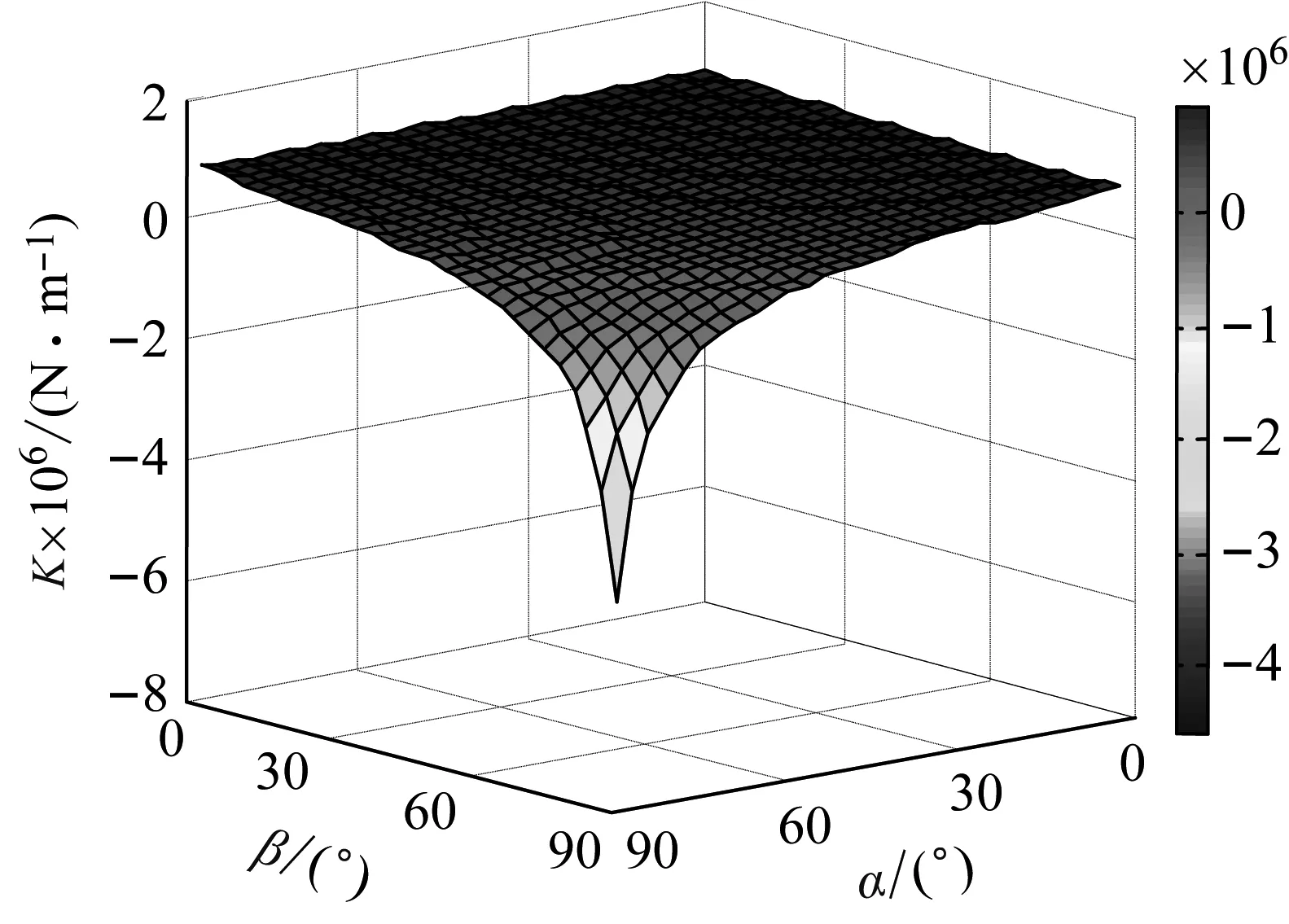
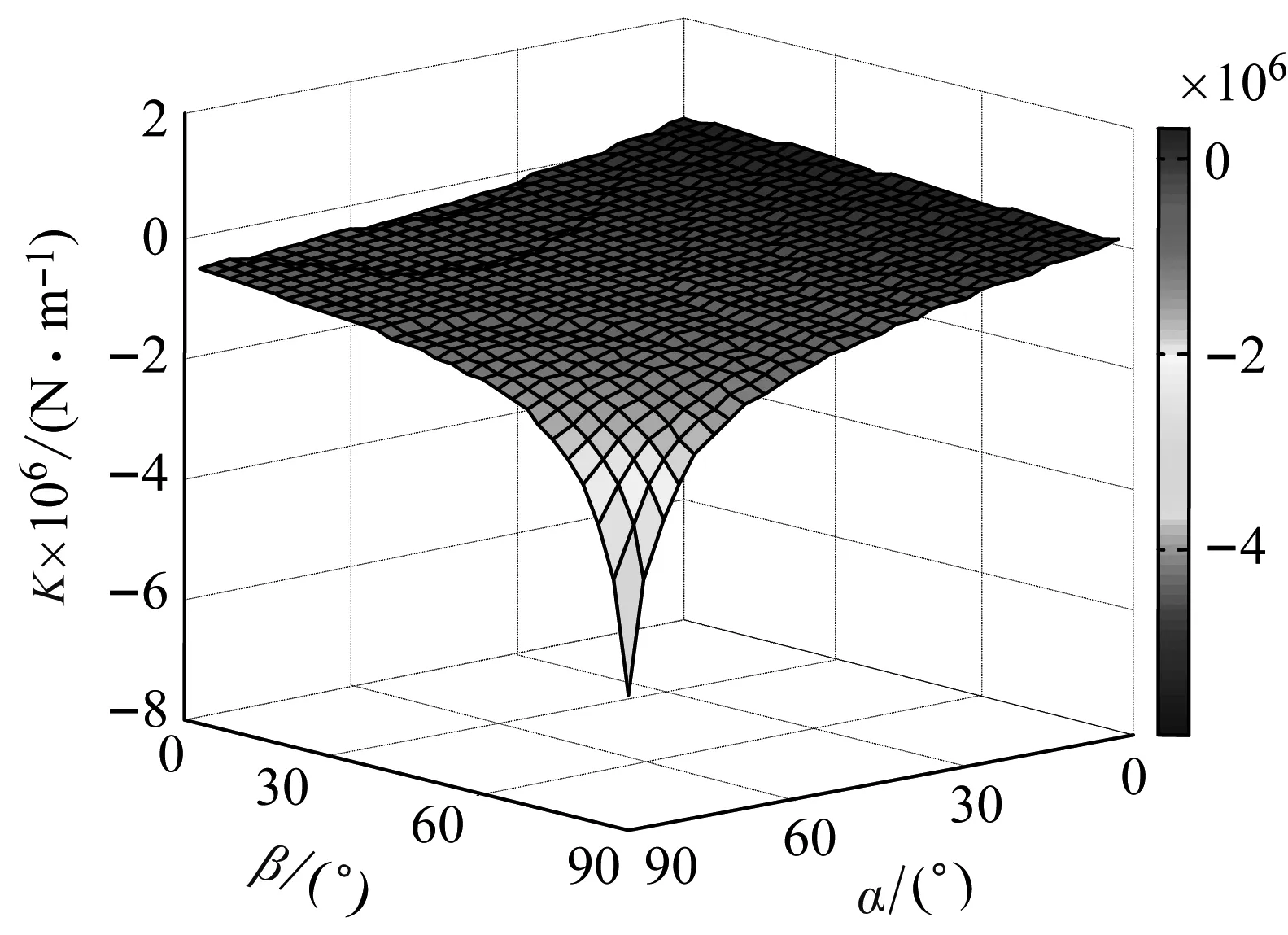
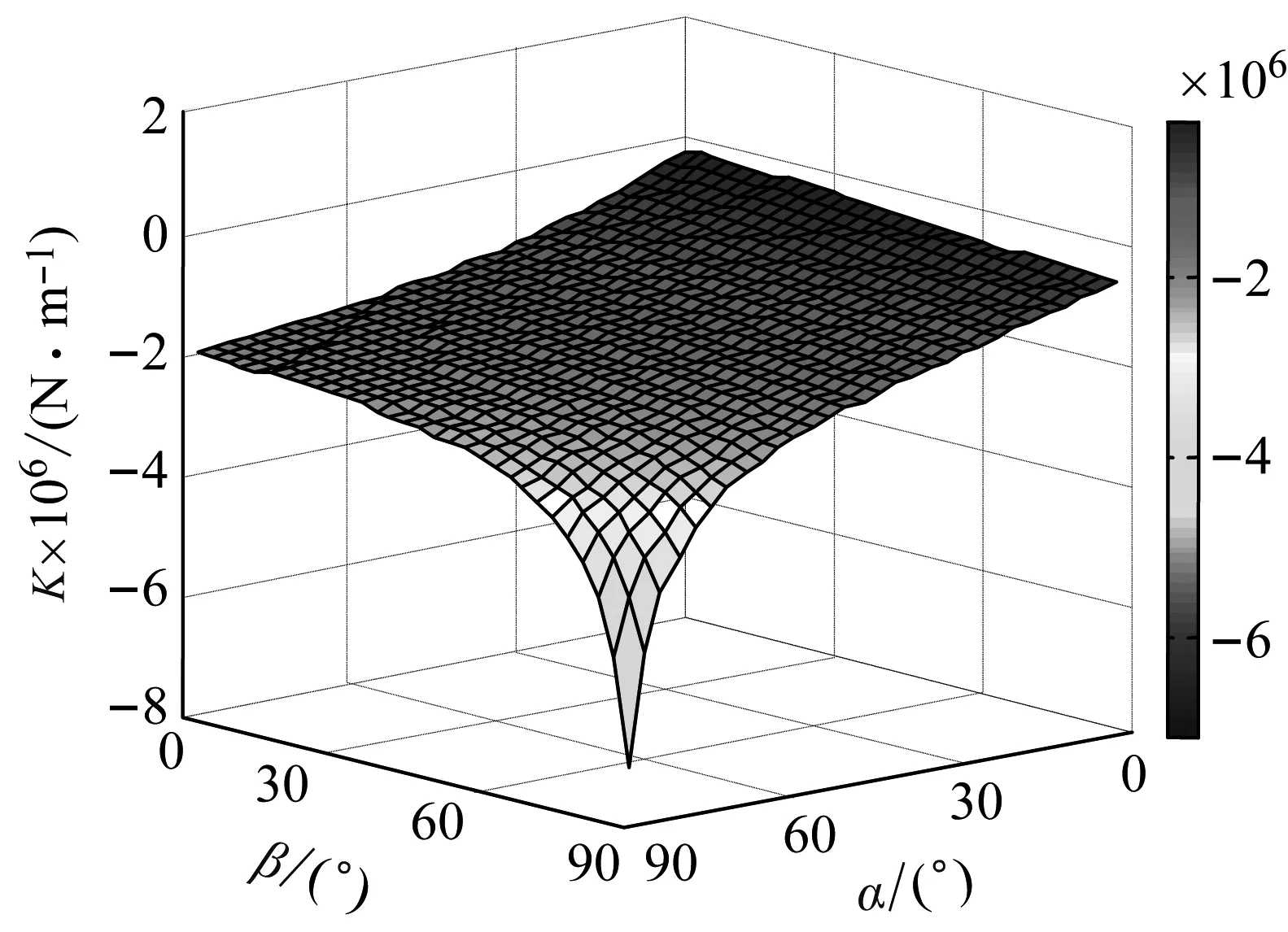
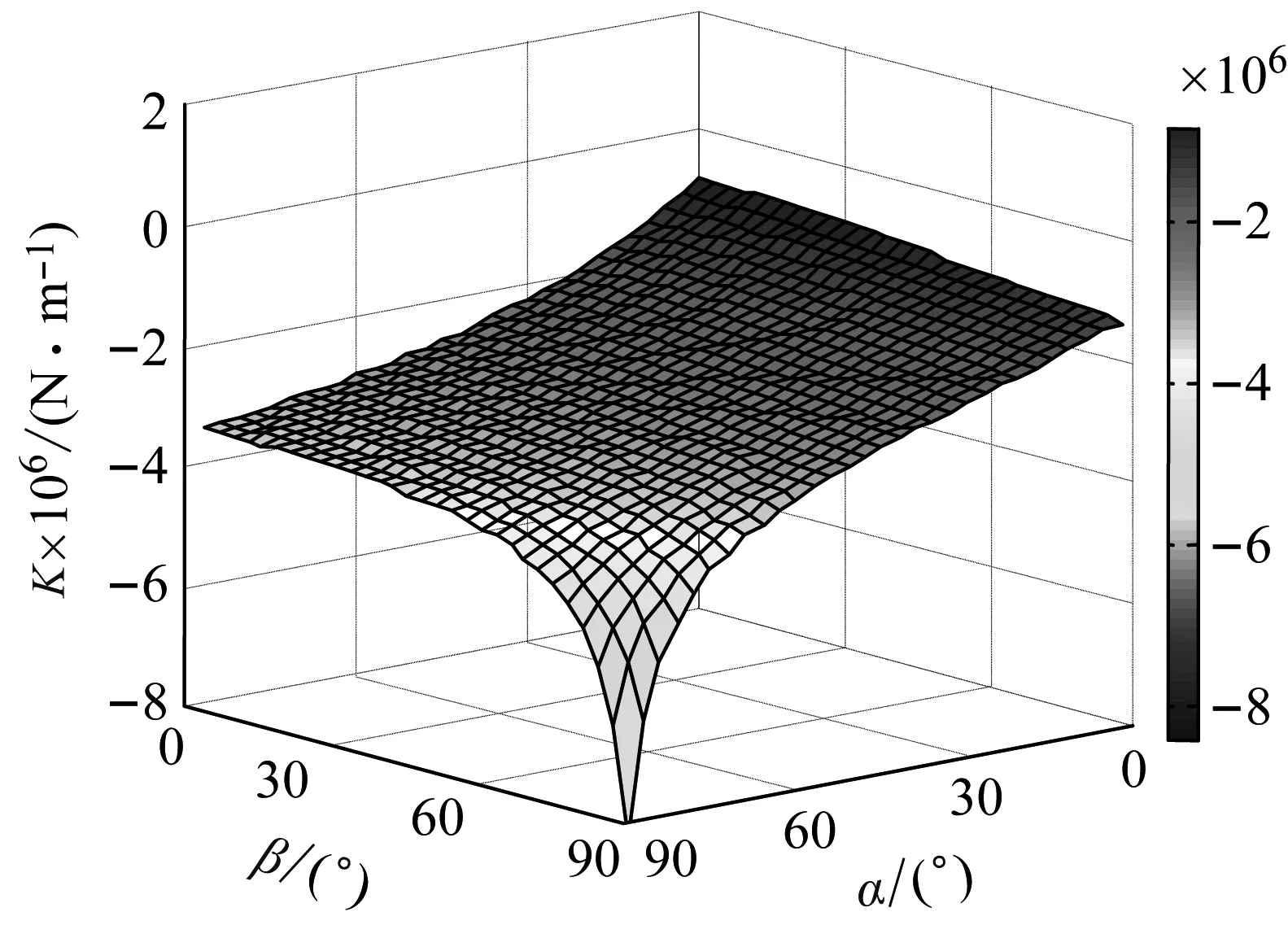
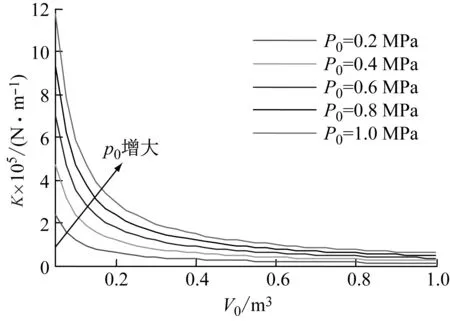
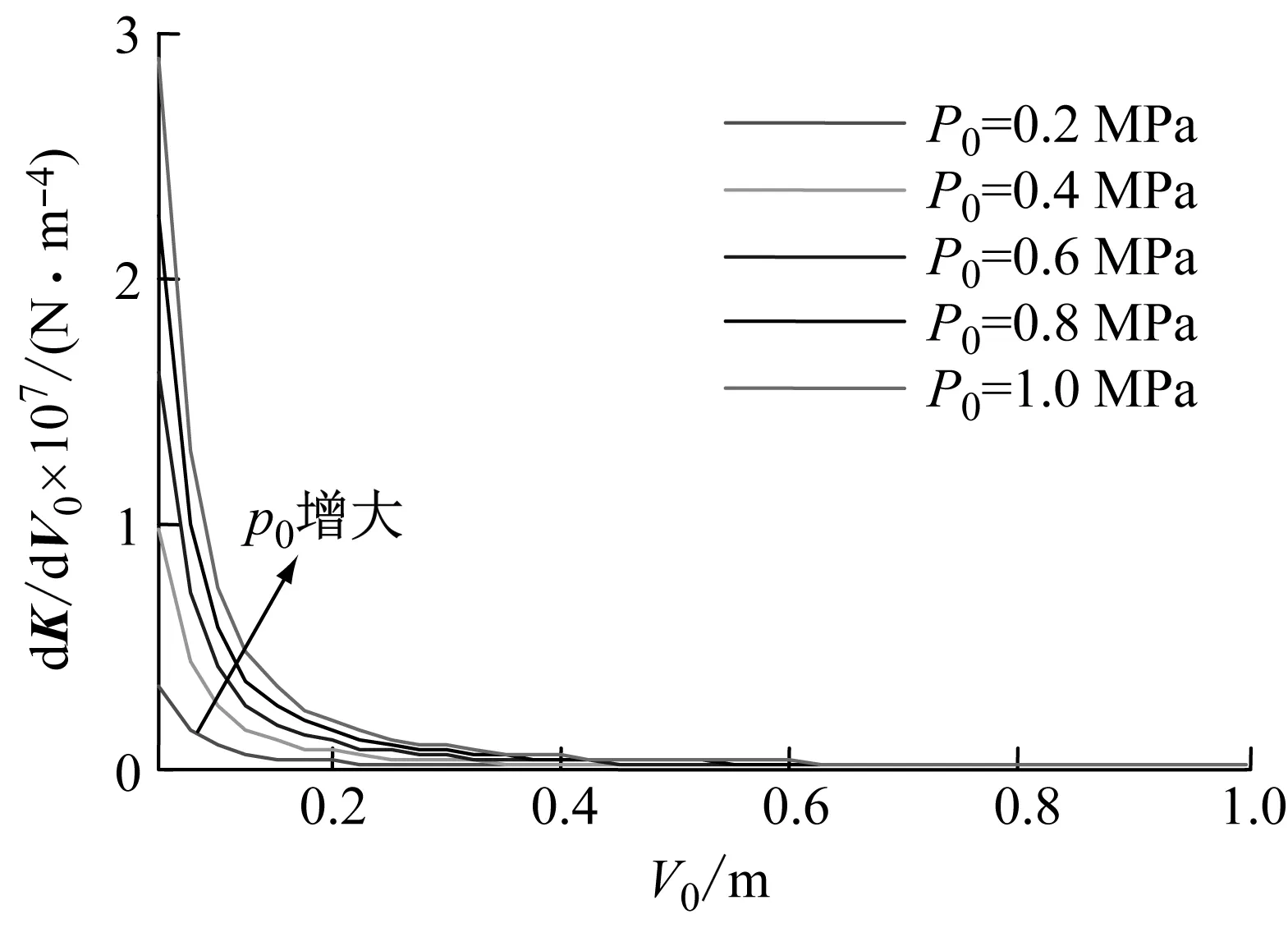
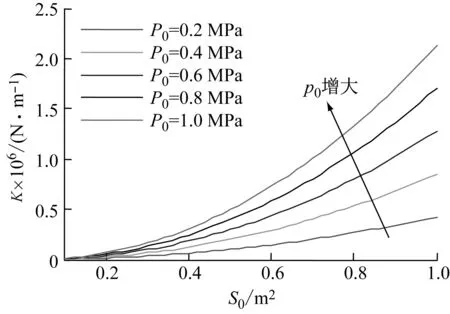
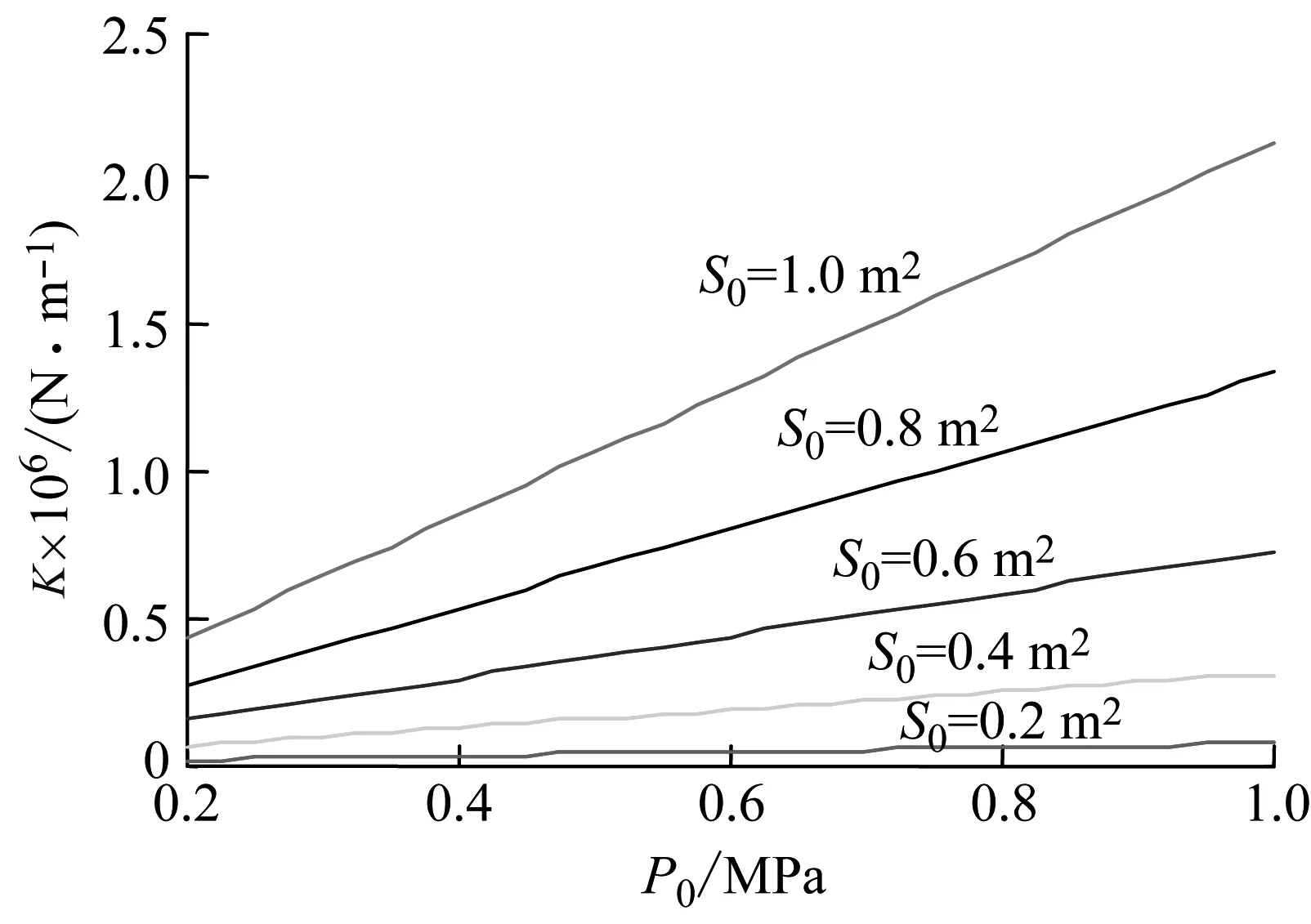
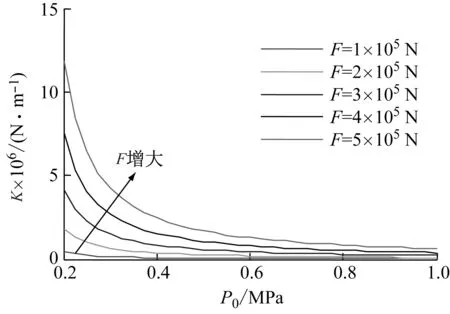
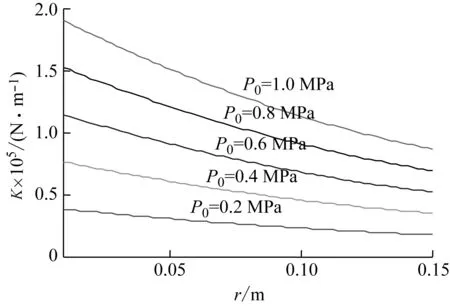
约束膜式空气弹簧的半剖面视图如图2所示,R为承载半径,r为弹性膜的圆弧半径,O为弹性膜的圆弧中心。弹性膜与上盖板交于点B2、与底座交于点C;过点O向直线DB2做垂线,垂足为点B;过点B的切线和铅垂线的夹角β为外角;过点C的切线和铅垂线的夹角α为内角;过点O的铅垂线,与上盖板交于点D。工作过程中,α发生变化,β保持不变;α和β的取值满足:0°≤α<90°,0°≤β<90°。上盖板承受载荷向下移动Δx,由MPB移至M1P1B3,过点O的铅垂线与上盖板的交点由D移至D1,弹性膜与上盖板的交点由B2移至B1,与下盖板的交点C保持不变。圆弧中心由O移至O1,沿垂向与水平向分别改变Δh、ΔR。过点O1向直线OD做垂线,垂足为点E;过点O1向直线P1B1做垂线,垂足为点B3。圆弧半径改变Δr,内角改变Δα,总弧长改变Δl。弧长变化量和垂向位移的比值定义为弧长变化率e,即:e=Δl/Δx。考虑弹性膜材料及隔振器结构特性,e的取值满足:0 eΔx=Δhcosβ-ΔRsinβ-Δxcosβ+ rΔα-(π+α+β)Δr (3) 图2中弹性膜的几何结构满足 ΔR=rcosα-(r-Δr)cos(α+Δα) (4) Δh=(r-Δr)sin(α+Δα)-rsinα (5) 如图3所示,过O点向直线O1B3做垂线,垂足为点b。Δr=OB-O1B3=BB1-O1b。其中,BB1=sinβΔx,O1b=O1a+ab=O1a+GO,O1a=O1Ecosβ=cosβΔR,GO=OEsinβ=sinβΔh,综上可得: Δr=sinβΔx-sinβΔh-cosβΔR (6) 联立式(3)~式(6)可得有效面积变化率 e(sinβ-sinα)+(π+α+β)sinαsinβ] (7) 其中:A=2+2cos(α+β)+(π+α+β)sin(α+β)。 图3 局部放大图Fig.3 Partial enlarged view 空气弹簧静平衡位置的体积V0=Vb+V1+V2+V3;向下移动Δx后的体积V=Vb+V4+V5+V6。Vb、V1、V2、V3、V4、V5、V6分别为多边形M1P1B1OCN、多边形M1MPDD1P1、梯形D1DBB1、扇形BOC、梯形OB1B3O1、扇形B3O1C与三角形COO1绕x轴旋转一周构成的回转体体积。 1.2.1 体积V0 多边形M1MPDD1P1绕x轴旋转一周构成的回转体积V1 V1=πR2Δx (8) V2=2πS1(R+y1)=πrcosβΔx(2R+rcosβ) (9) 图4 梯形D1DBB1回转体Fig.4 Rotation of trapezoidal D1DBB1 图5中扇形BOC的面积S2=0.5(π+α+β)r2,质心Z2到x轴的距离R+y2=R+OZ2sin[(β-α)/2],其中OZ2=4/3r(π+α+β)×sin[(π+α+β)/2],由巴普斯定理可得V3 (10) 图5 扇形BOC回转体Fig.5 Rotation of sector BOC 联立式(8)~(10)可得V0 V0=Vb+πRΔx(R+2rcosβ)+ (11) 1.2.2 体积V y3=(OB1-Z3F)cosβ,Z3F=I3-B1Etanβ= I3-(B1B3-d3)×tanβ 综上,R+y3=R+OB1cosβ-[I3-(B1B3-d3)tanβ]×cosβ,由巴普斯定理可得V4 V4=2π(R+y3)S3=πrΔx(2R+rcosβ)× (12) 图6 梯形OB1B3O1回转体Fig.6 Rotation of trapezoidal OB1B3O1 将r=r-Δr,R=R-ΔR,α=α-Δα代入式(10)可得V5 (13) 同理,图7中三角形COO1的面积S4=0.5r2Δα,质心Z31到x轴的距离R-y4=R-(ΔR+rcosα)/3,由巴普斯定理可得V6 V6=2π(R-y4)S4=πr2(R-rcosα/3)Δα (14) 图7 三角形COO1回转体Fig.7 Rotation of triangle COO1 联立式(12)~(14)可得V α+β)sinφ]}-πr3Δαcosα+2πRr2Δα- πr2ΔR(π+α+β)-2πRrΔr(π+α+β)- 2πr2Δr(sinβ-sinα) (15) 1.2.3 体积变化率dV/dx 由式(11)与(15)可得体积变化率 (16) 其中: (2sinβ-sinα)sin(α+β)-(π+α+β)(sinα- ρ=0对应的特征方程满足式(17)。S0=0.283 m2、V0=0.046 m3、R=0.3 m、r=0.055 m,式(17)对应的特征曲面如图8所示。弧长变化率、内角和外角在特征面上取值时,体积变化率模型与文献[19]相同,且不受弧长变化率、内角与外角影响;取值低于特征面时,体积变化率大于文献[19],反之小于。 图8 ρ=0对应的特征曲面Fig.8 Characteristic surface of ρ=0 (17) 其中: cosβ)+(2sinβ-sinα)sin(α+β)- (π+α+β)(sinα-sinβ)] 如图9(a)所示,S0=0.283 m2、R=0.3 m、r=0.055 m,e=0时,κ>1,体积变化率大于文献[19],且随内角和外角的增大而增大。对比图9(b)~(d)可知,e≠0时,κ<1,体积变化率小于文献[19];α→90°,β→90°和α→0°,β→0°,κ增幅显著;κ随弧长变化率的增大逐渐减小至负数,即体积变化引入的正刚度变为负刚度。因此,弹性膜变形引起的腔室体积变化在刚度计算过程中不能忽略。 (a) e=0 (b) e=4 (c) e=8 (d) e=12图9 不同弧长变化率下的κFig.9 κ at different arc length gradients 联立式(2)、式(7)与式(16)可得刚度 sinα)sin(α+β)-(cosα+cosβ)- (18) K=0对应的特征方程如式(19)。S0=0.283 m2、V0=0.046 m3、P0=0.501 MPa、R=0.3 m、r=0.055 m,式(19)对应的特征曲面如图10所示。由图10与图11可知,弧长变化率、内角和外角的取值高于图10中的特征面时,刚度K>0,空气弹簧稳定;反之不稳定。 [sin(α+β)+(π+α+β)sinαsinβ]+ (19) 其中: cosβ)-(π+α+β)(sinα-sinβ)] 图10 K=0的特征曲面Fig.10 Characteristic surface of K=0 图11 T随α、β的变化规律Fig.11 Variation of T with α and β 文献[12]中,空气弹簧的刚度理论模型假设e=0,dV/dS=-S0,即刚度K为 (20) 其中: 文献[16]仍保持假设e=0成立,但是推导得到dV/dS=-S0(1+Ψ),即刚度K为 (21) 其中: A=2+2cos(α+β)+(π+α+β)sin(α+β) 文献[19]仍沿用dV/dS=-S0,但是考虑了弧长变化率e对垂向刚度的影响。即刚度K为 (22) 将HIT300约束膜式空气弹簧作为研究对象验证所建理论模型的正确性。由文献[19]可知,HIT300约束膜式空气弹簧的参数α=0°、β=75°、S0=0.283 m2、V0=0.225 m3、P0=0.201 MPa、R=0.3 m、r=0.055 m,e=0.147,实测刚度为54.92 N/mm。将上述参数代入不同理论模型,计算得到的刚度值如表1所示。 表1 不同理论模型计算得到的刚度 由表1可知,由改进刚度理论模型计算得到的刚度值与实测刚度值的偏差为9.67%,比文献[12]与[13]中的模型精度提高7.63%;相比文献[16]与[19],模型精度均有所提高;验证了所建理论模型的正确性。 弧长变化率对刚度的影响规律如图12所示。S0=0.283 m2、V0=0.046 m3、P0=0.501 MPa、R=0.3 m、r=0.055 m,刚度随内角、外角以及弧长变化率的增大而减小,因此适当增大内角、外角和弧长变化率可降低刚度,实现环境微振动的低频/超低频隔振效果。 参数e=1,α=0°,β=80°下,充气压强、腔室体积、有效面积、负载及弹性膜的圆弧半径对刚度的影响规律如图13~图16所示。由图13可知,刚度随充气压强的减小而减小,随腔室体积的增大而减小。腔室体积较小时,刚度随腔室体积的增大而显著降低;超过拐点0.4 m3,增大腔室体积对刚度的衰减效果甚微。此外,较大的腔室体积也对安装空间提出了较高的要求。 (a) e=0 (b) e=4 (c) e=8 (d) e=12图12 不同弧长变化率下的刚度Fig.12 Stiffness at different arc length gradients (a) K-V0曲线 (b) dK/dV0-V0曲线图13 不同充气压强下的K-V0曲线Fig.13 K-V0 curves at different pressures (a) 不同充气压强下的K-S0曲线 (b) 不同有效面积下的K-P0曲线图14 刚度的影响因素Fig.14 Influencing factors of stiffness 如图14所示,最佳腔室体积0.4 m3下,刚度随有效面积呈指数规律增大,随充气压强线性增大。将S0=F/(P0-Pa)代入式(18)可得刚度与负载满足如式(24)。由图15所示的特征曲面可知,相同充气压强下,刚度随负载的增大而增大;相同负载下,高充气压强的工作方式及小有效面积的结构设计更有利于实现低频/超低频隔振效果。由图16可知,弹性膜的圆弧半径越大,相同负载下的刚度越小;且弹性膜的圆弧半径刚度的影响效果随充气压强的增大而增大。 β)[sin(α+β)+(π+α+β)sinαsinβ]+ (23) [(2sinβ-sinα)sin(α+β)-(cosα+cosβ)- (24) 其中: 图15 不同负载下的K-P0曲线Fig.15 K-P0 curves at different loads 图16 不同充气压强下K-r曲线Fig.16 K-r curves at different pressures 本文兼顾弹性膜弧长变化及其变形引起腔室体积变化,建立了约束膜式空气弹簧的改进刚度模型,有效解决了空气弹簧实际刚度与理论值相差较大的问题。仿真分析弹性膜弧长变化率及几何结构参数对刚度的影响规律,进而针对环境微振动的低频/超低频隔振需求,提出实现低刚度隔振特性的结构及材料参数。通过研究得出以下结论: (1) 弹性膜弧长变化及其变形引起的腔室体积变化对刚度的影响均不能忽略。 (2) 弧长变化率e=0时,体积变化率随α和β的增大而增大。弧长变化率e≠0时,体积变化率随弧长变化率的增大而减小,弧长变化率增大到一定程度,腔室体积变化引入的正刚度变为负刚度特性。 (3) 刚度随弧长变化率、内角、外角、圆弧半径与腔室体积的增大而减小。腔室体积较小时,刚度随腔室体积的增大显著减小,超过拐点0.4 m3,增大腔室体积对降低刚度的效果甚微。 (4) 刚度随充气压强线性增大,随有效面积呈指数规律增大。定负载下,高充气压强的工作方式及小有效面积的结构设计有利于实现低频/超低频隔振效果。 本文的研究为超精密加工与测量、光学加工与装配、高精度惯导器件加工和设备装配、超大规模集成电路制造等领域中低频/超低频空气弹簧的结构优化设计及精密加工提供了有效的理论依据。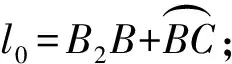
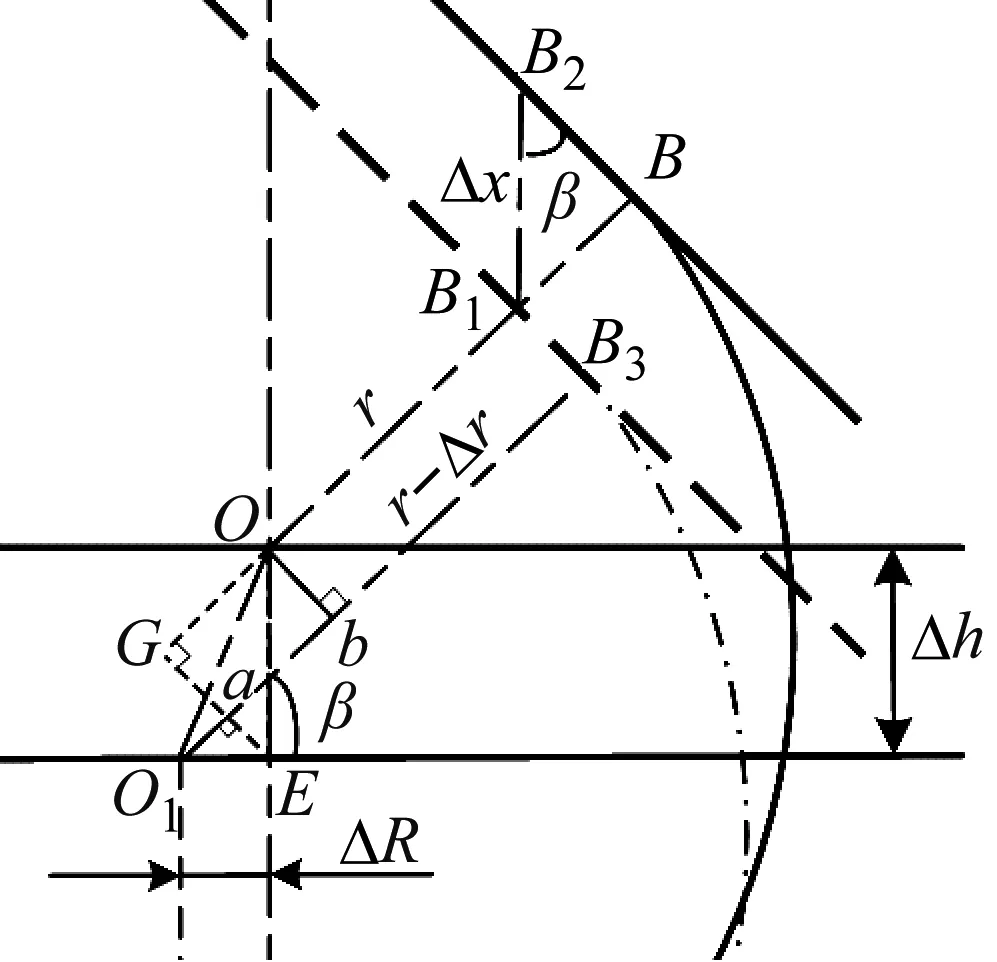
1.2 有效体积变化率
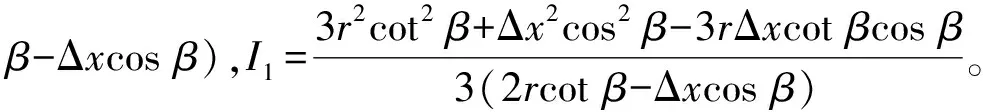
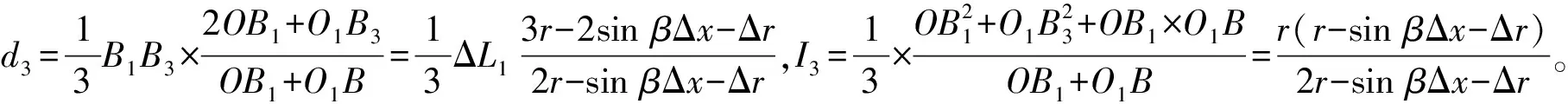
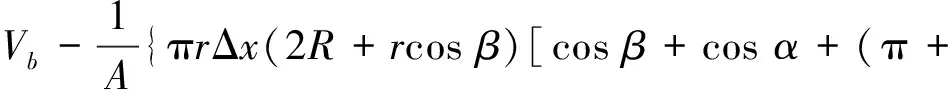
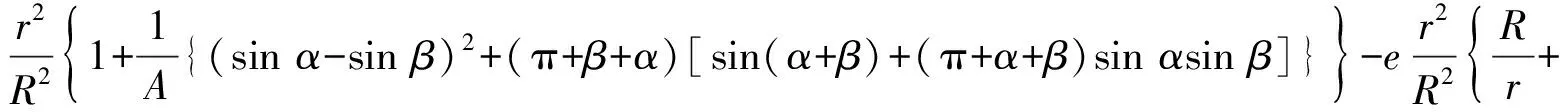

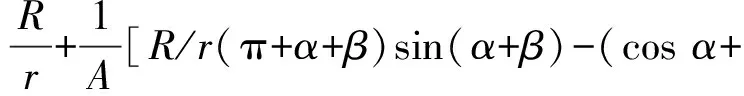
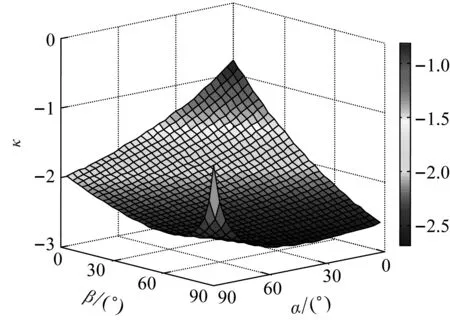
1.3 刚度
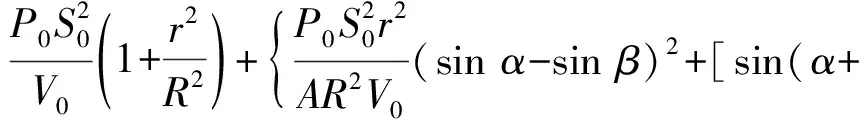
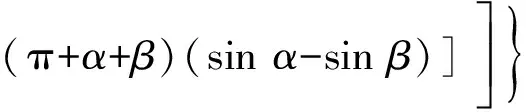
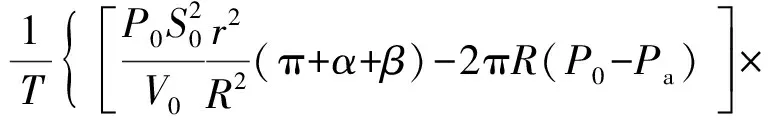
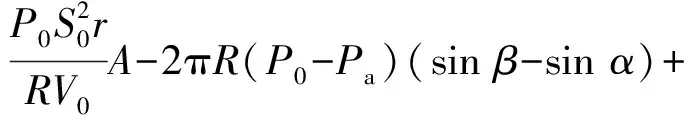
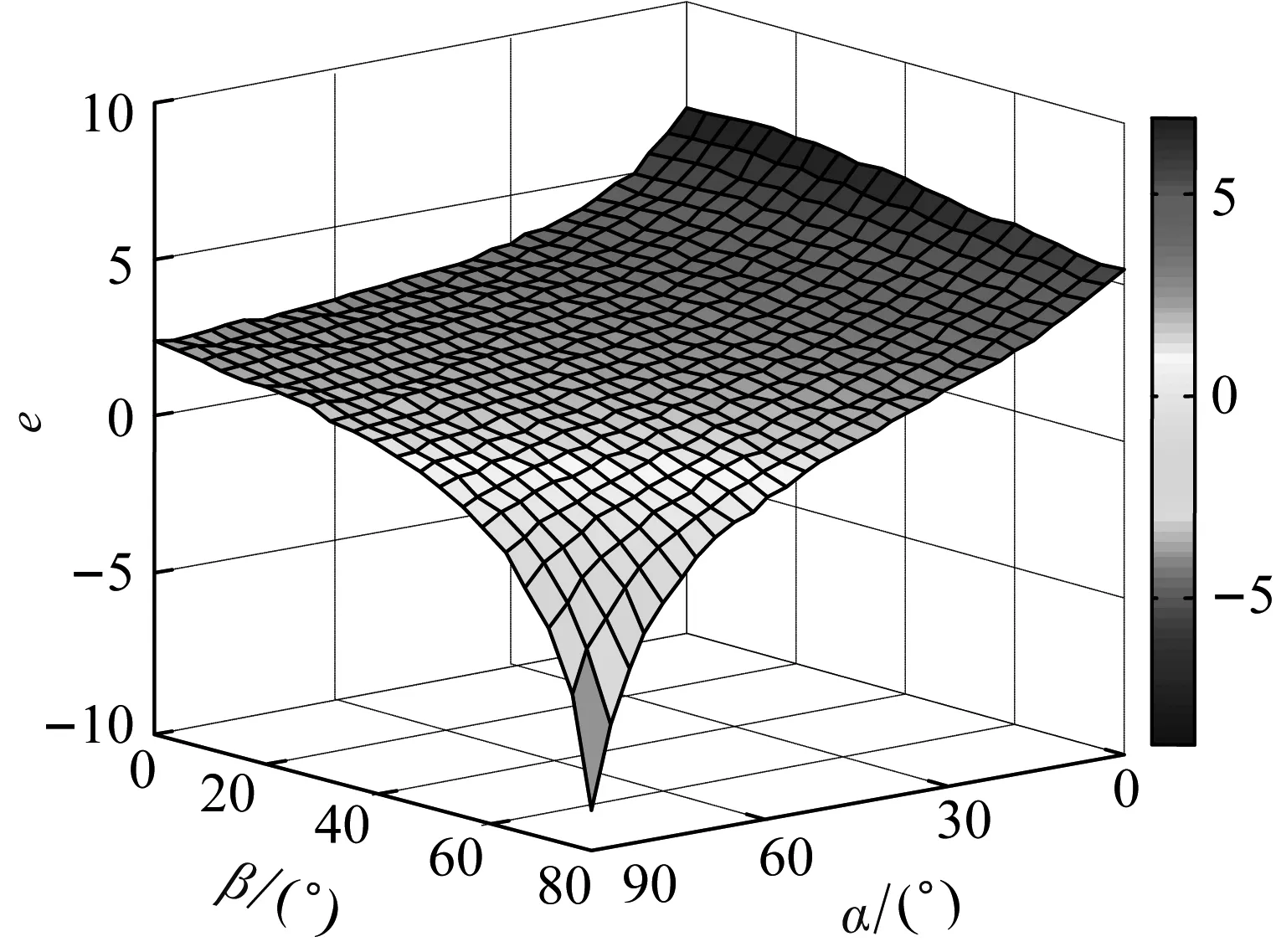
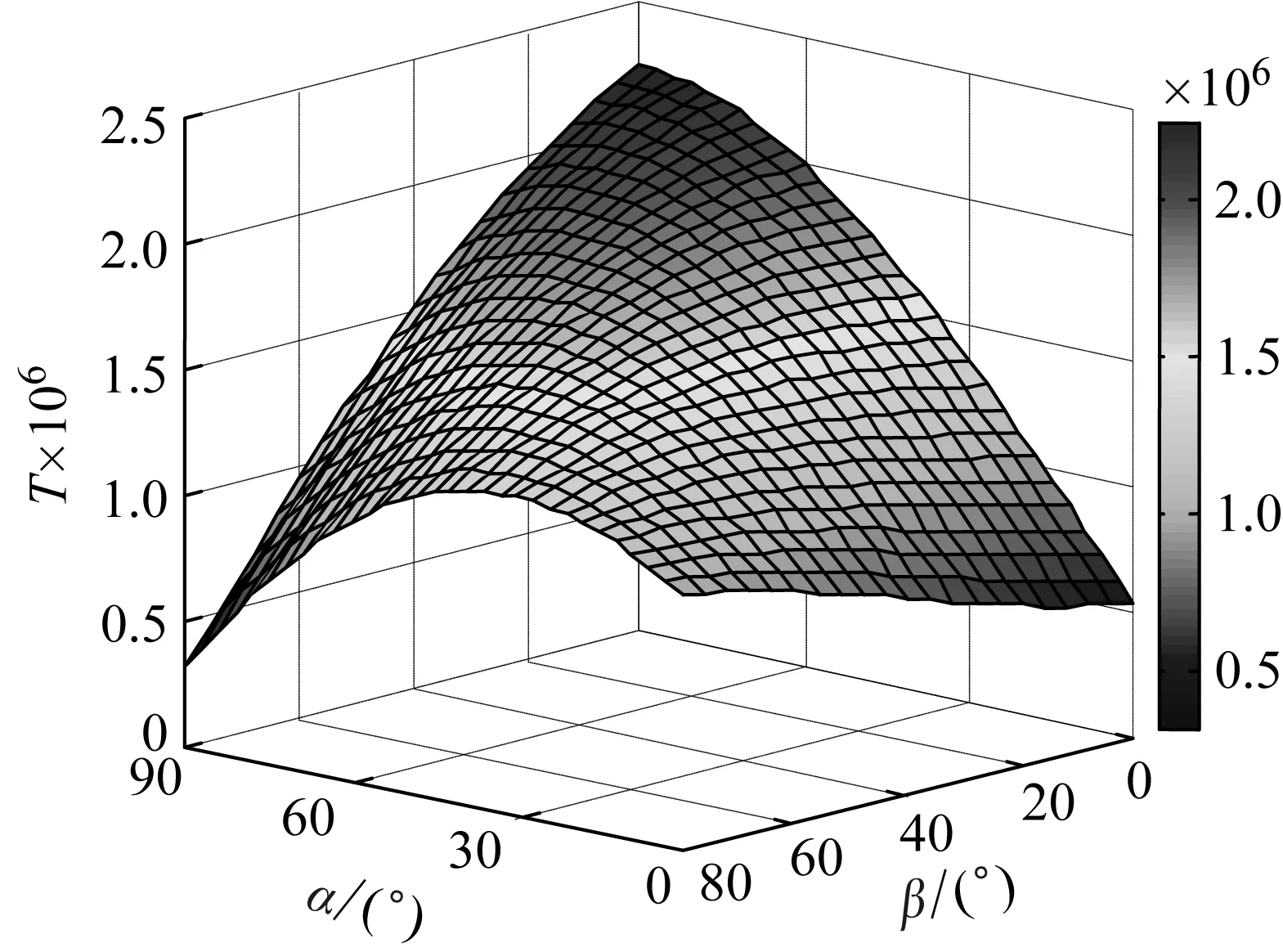
1.4 算例验证
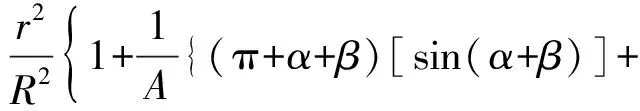
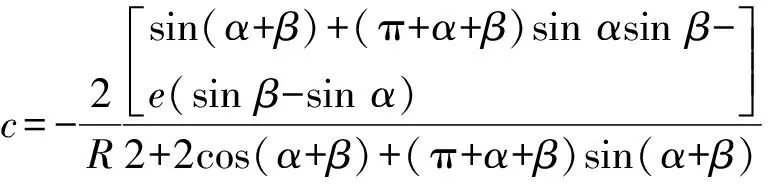
2 刚度分析
2.1 弧长变化率的影响分析
2.2 其他影响因素分析
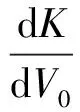
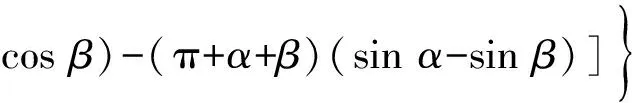
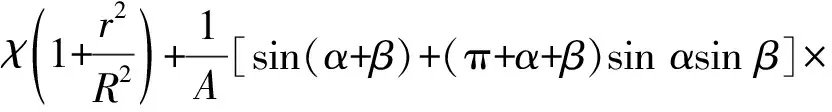
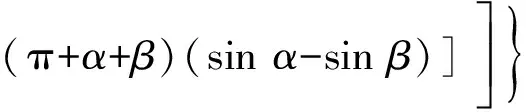
3 结 论
