广义分数阶van der Pol-Duffing振子的动力学响应与隔振效果研究

唐建花, 李向红,3, 王 敏, 申永军, 李壮壮

(1.石家庄铁道大学 数理系,石家庄 050043； 2.石家庄铁道大学 机械工程学院,石家庄 050043；3.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

非线性系统在各种扰动下会产生许多复杂的现象，如主共振、超谐共振、亚谐共振、内共振等，求解该类系统的方法有很多，如平均法、增量谐波平衡法、改进的谐波平衡法、改进的多尺度法等[1-7]。当激励频率和系统的固有频率接近时，系统往往会发生共振。在工程设计过程中，如果合理设计参数，可有效避开共振带来的危险因素；同时，在某些情况下，也可更好地利用有效振动。针对非线性系统共振的研究，许多学者已经做了大量的工作，Nayfeh[8]针对单自由度系统，通过添加具有适当振幅和相位的超谐波激励来减少、消除或增强共振的响应。Glebov等[9]讨论了WKB法在主共振方程摄动问题中的适用性。Sun等[10]通过调制不同周期信号或噪声水平来控制、激发或抑制双稳态系统的共振行为。毛晓晔等[11]用多尺度法研究了超临界流速输液管在3∶1内共振条件下的稳态幅频响应。Xia等[12]揭示了在超临界状态下Timoshenko管道强迫振动的多重共振响应。Mao等[13]提出了一种解决具有强非线性和非均匀边界条件结构振动的分析方法，并将其用到钢筋的纵向振动和非线性扭转边梁中，发现该方法对具有非线性和非均匀边界条件的复杂结构的振动分析具有很好的作用。胡宇达等[14-15]分别研究了轴向变速运动载流梁的联合共振和旋转运动圆环板、导电旋转圆板在磁场环境下的动力学行为。

近年来，有些学者发现分数阶微分更能描述材料分数阶黏弹性特征，因此，对系统主共振的研究逐渐由整数阶向分数阶拓展。Shen等[16-18]用平均法和增量谐波平衡法计算了分数阶微分自激系统、非线性时滞分数阶系统和单自由度分数阶分段光滑系统的解析解并分析了其动力学行为。Chen等[19]使用广义谐和变换法得到了随机分数阶系统的不含分数阶导数项的等价随机系统，然后使用随机平均法给出了系统的解析解。Leung等[20]提出了一种针对分数阶导数自治和非自治系统的改进谐波平衡方法，并研究了激励频率、分数阶、幅度、相位角和频率之间的相互作用。基于第一类传递函数的基本属性，Malti等[21]根据Matignon稳定性定理的推论给出了第二类传递函数的共振条件。为满足工程需要，需用不同的方法对共振带来的危害进行抑制和控制，如隔振[22]、减振[23-24]、缓冲[25]等。含分数阶算子的动力学模型能够准确地描述黏弹性材料隔振器的动态特性。因此，为尽可能减少机械或工程结构振动引起的危害，含分数阶项的隔振技术在工程中已经得到了广泛应用。周超等[26]用谐波平衡法研究了由基础振动激励、黏弹性材料隔离的被动隔振体的非线性动力响应。Makris等[27]提出了可用于管道系统，锻造锤和其它工业设备以及建筑结构隔振的分数阶导数Maxwell黏性阻尼器。Alberto等[28]给出了分数阶被动隔振系统模型，并分析了隔振器刚度和阻尼频率的影响。

前人针对分数阶van der Pol-Duffing 振子的研究大多在解析解方面，很少有学者考虑其隔振效果。因此，本文将提出具有非线性阻尼的分数阶van der Pol-Duffing振子，称之为广义分数阶van der Pol-Duffing振子，并重点分析在无量纲情况下该振子的动力学行为和隔振效果。类似的阻尼项已在模拟人体在刚性地板上行走的侧向力和船舶的侧倾运动中被讨论过并取得了很好的效果[29-30]，但是这些系统均为整数阶系统。本文在研究过程中，采用平均法得到该振子的一阶解析解，进而分析定常解的动力学行为，并讨论无量纲化后各个参数对响应和力传递率的影响，其分析方法和结论不仅能为该类振子的隔振设计和隔振效果评价提供一定的理论参考，而且可以使工程设计人员对分数阶振子的隔振特性有更进一步的了解，同样对系统动力学特性的研究有着很重要的参考意义。

1 具有分数阶导数阻尼的广义 van der Pol-Duffing 振子

广义分数阶 van der Pol-Duffing 振子可表示为

(1)

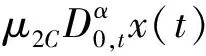
(2)

式(1)可变形为

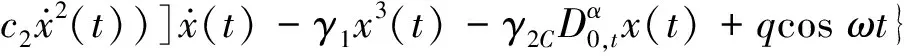
(3)

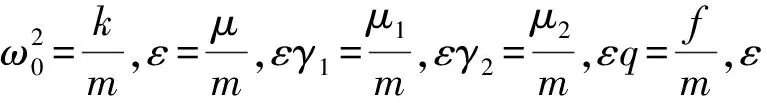
2 广义 van der Pol-Duffing 振子的近似周期解

本节用平均法研究激励频率接近固有频率时广义分数阶van der Pol-Duffing振子的一阶解析解。

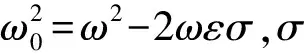
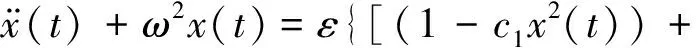
2ωσx(t)+qcosωt}

(4)

设式(4)有如下解

x=acosφ

(5a)

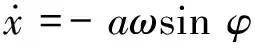
(5b)

假定φ=ωt+θ,a和φ为幅值和相位。对式(5)求导可得

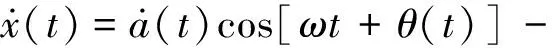
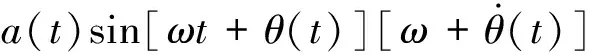
(6a)

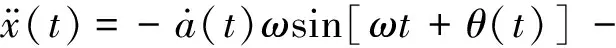
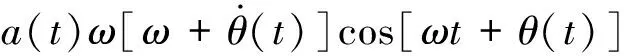
(6b)

因为振幅a和相位φ变化缓慢, 可令

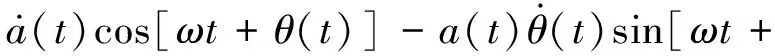
θ(t)]=0

(7)

将式(5a)和(6b)代入式(4)中,用平均法在一个周期上进行平均, 可得

(8a)

(8b)

其中

Y1(a,θ)=ε[qcos(φ-θ)+2aωσcosφ-a3γ1cos3φ]+

(-8aεωsinφ+a3εc1ωsinφ+3a3εc2ω3sinφ+

a3εc1ωsin 3φ-a3εc2ω3sin 3φ)/4

(9a)

(9b)

式中：t∈[0,T],如果被积函数为周期函数, 则T=2π；如果被积函数非周期,则T=∞。因此式(8)可化简为

a1+a2

(10a)

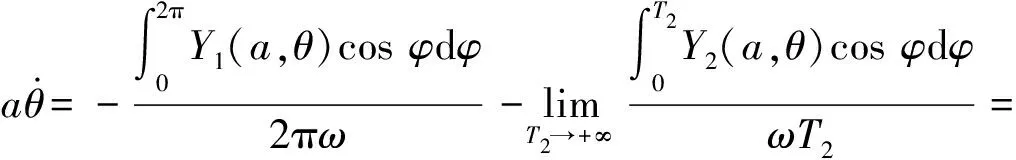
(10b)

其中

(11a)

(11b)

因为

所以

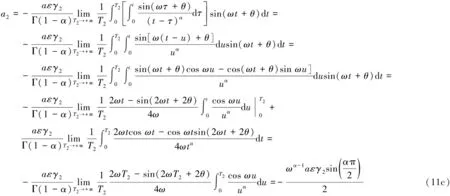
(11d)

因此

(12a)

(12b)

将原系统参数代入式(12)可得

(13a)

(13b)

3 定常解及其稳定性

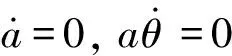
(14a)

(14b)

其中

(15a)

(15b)

由式(15)可得,如果分数阶阶次α→1时,C(α)=2μ-μ2ωα-1,K(α)=k,分数阶导数项只表现阻尼特性而不呈现刚度特性。当分数阶阶次α→0时,C(α)=2μ,K(α)=k+μ2ωα,分数阶导数项只呈现刚度特性, 这说明了分数阶器件与整数阶的不同之处, 即通过适当控制分数阶阶次可使分数阶器件同时表现阻尼和刚度特性。因此, 分数阶导数项可以分解为线性弹性恢复力和线性阻尼之和,也即

(16)

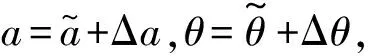
(17a)

(17b)

因为

(18a)

(18b)

所以

(19a)

(19b)

特征方程为

λ2-(b11+b22)λ+b11b22-b21b12=0

(20)

其中

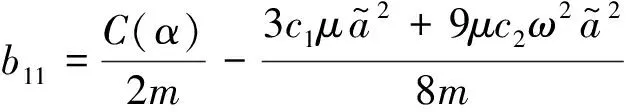
当P=b11+b22≤0,Q=b11b22-b21b12>0时,特征值的实部为负,即定常解是稳定的,反之亦然。

为验证解析解的正确性,令参数m=5、k=15、μ=0.5、c1=3、c2=2、μ1=15、μ2=0.5、α=0.3,f分别为0.2、0.5和1.2, 对式(14a)和式(4)进行数值模拟, 结果如图1所示, 其中实线和虚线分别表示稳定和不稳定解析解, “+”表示数值模拟结果。数值模拟结果采用文献[31]中提出的分数幂级数法处理, 其中步长为0.003, 计算时间为800 s,将后640 s响应的最大幅值视为稳定幅值。根据图1可得, 数值结果和稳定解析解吻合很好。因此, 本文采用平均法得到的解析解精确度较高, 可用于实际工程的参数设计或分析中。

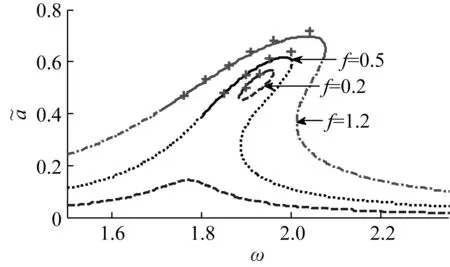
图1 解析解和数值解对比Fig.1 Comparison of analytical solution and numerical solution

4 系统参数对响应特性的影响

为深入分析该系统的响应特性, 引入下列无量纲量

其中,ξ、A0、ζ、κ1、F和κ2分别代表阻尼比、振幅、频率比、非线性刚度系数、激励幅值和分数阶项系数,χ1和χ2为非线性参数。式(14a)可变为

(21)

由式(21)得, 幅值最大值满足的方程为

(22)

无量纲化后, 判别解稳定性的特征方程为

λ2-P1λ+Q1=0

(23)

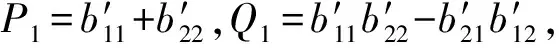
令基本参数κ1=5、κ2=0.3、χ1=0.05、χ2=0.854、α=0.3、F=0.5、ξ=0.5。假设其余参数保持基本参数值不变,只改变其中某个参数并讨论其对响应的影响,如图2～8所示。由图2～8可得, 在给定参数范围内,随着κ1、κ2、χ1、χ2、α、F和ξ的变化, 解的稳定性、解的个数、共振区域、共振频率、曲线弯曲程度和共振峰峰值均有变化, 多值解稳定性的变化使得解产生跳跃现象, 其中最大支、中间支、最小支分别被称为稳定共振支, 不稳定支、非共振支。设计系统时, 应当避免或减小不稳定区域的出现。

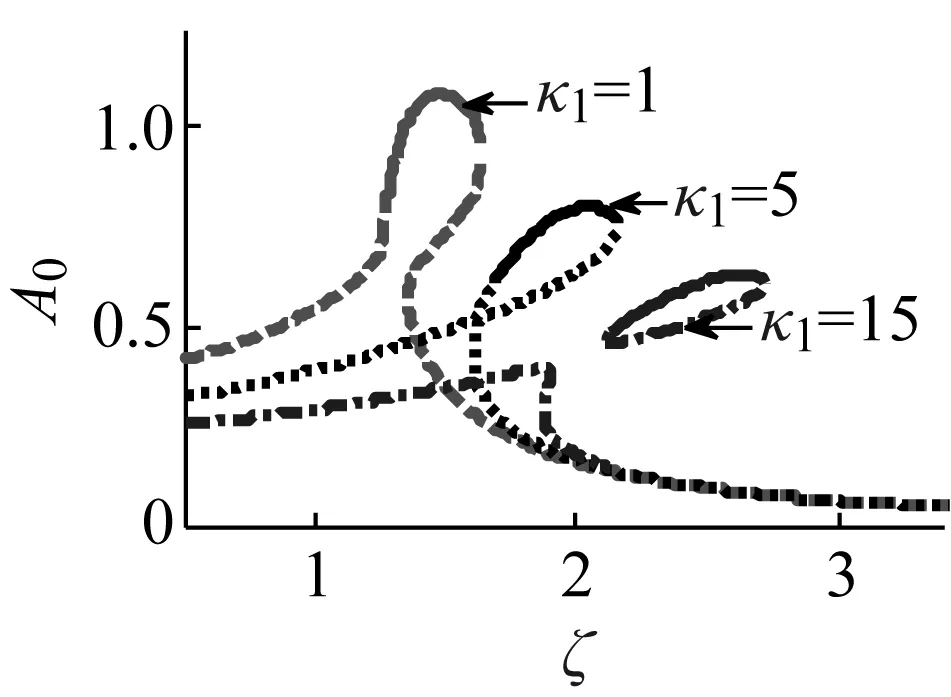
图2 非线性刚度系数κ1

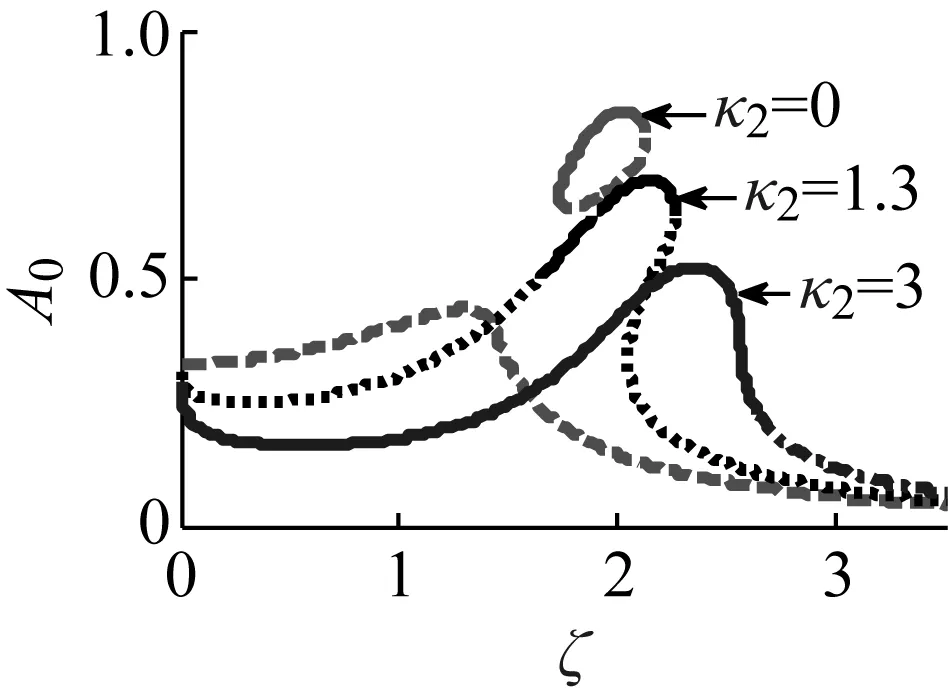
图3 分数阶项系数κ2 对响应的影响

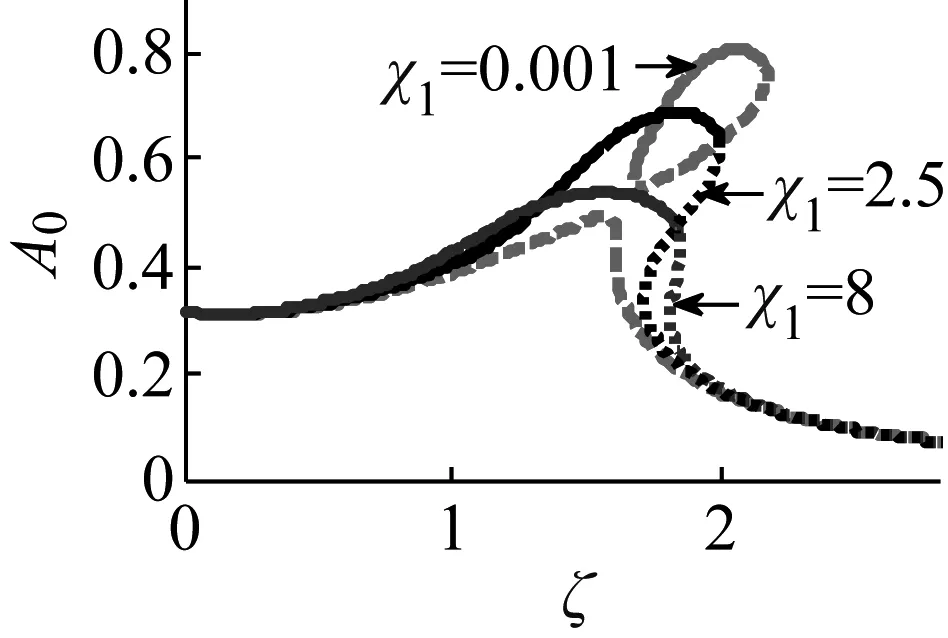
图4 参数χ1对响应的影响

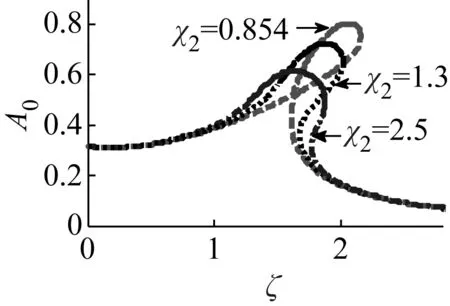
图5 参数χ2对响应的影响

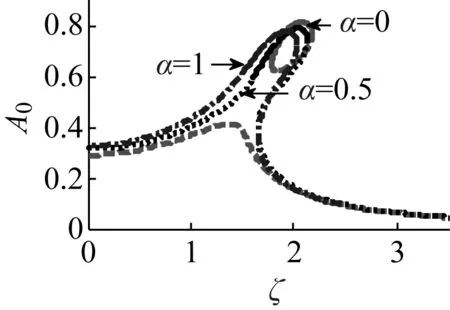
图6 分数阶阶次α对响应的影响

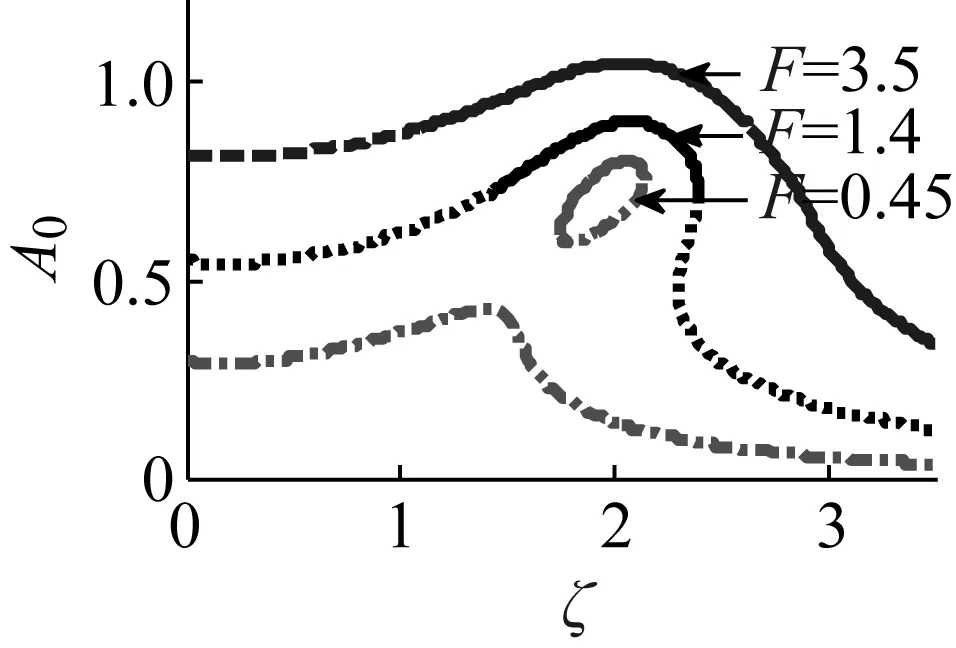
图7 幅值F对响应的影响Fig.7 Effect of amplitude F on response

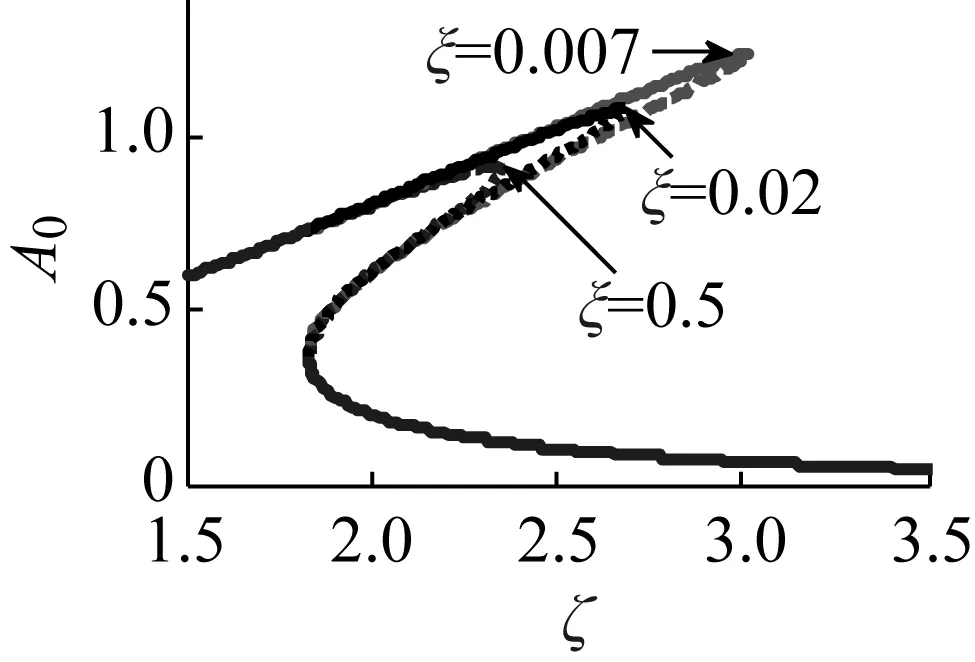
图8 阻尼比ξ对响应的影响Fig.8 Effect of damping ratio ξ on response

当非线性刚度系数κ1分别为1、5、15,其他参数保持基本参数不变时,作出幅频曲线图,如图2所示。由图2可得,随着κ1的增大,闭合曲线逐渐形成且离光滑曲线越来越远,多值解和跳跃现象一直存在,稳定共振支区域增大,非共振支一直不稳定,共振频率增大,共振峰向频率增大方向移动,幅值减小,因此,非线性刚度系数对响应的共振峰峰值有抑制作用。

当分数阶项系数κ2分别取0、1.3、3,其他参数保持基本参数不变时,系统幅频曲线的变化图,如图3所示。由图3可得,随κ2的增大,闭合曲线逐渐破裂而形成一条平滑曲线,曲线弯曲程度和幅值逐渐减小,共振区域、稳定解区域和共振频率增大,共振峰向频率增大方向移动,多值解逐渐消失,稳定单值解区域渐渐增大,因此,在选取κ2时需稍大一些,但频率不要太大。

当χ1的取值分别为0.001、2.5和8,其他参数保持基本参数不变时,其幅频曲线变化图如图4所示,同时给出χ2分别为0.854、1.3和2.5时的幅频曲线变化图,如图5所示。图4和图5的动力学行为类似，但它们对接下来力传递率的影响稍有不同,因此,在这里同时讨论了图4和图5的动力学行为。由图4和图5可得,随参数的增大,闭合曲线消失,曲线逐渐平缓,多值解范围渐渐减小,共振区域变大且共振峰向频率减小方向移动,共振频率和幅值减小,稳定解基本保持在共振区域内,因此,χ1,χ2的增大会抑制共振峰值增大,但跳跃行为减弱。

当分数阶阶次α分别为0、0.5和1,其他参数保持基本参数不变时,图6给出α对幅频曲线的影响。由图6可得,共振区域、共振峰、共振频率和幅值的变化规律与图4和5相似,刚度特性随α的增大而减小,这导致共振频率逐渐减小且曲线逐渐平缓,阻尼特性随α的增大而增大,因此系统共振振幅逐渐减小,多值区稳定共振解、不稳定解、不稳定非共振解一直存在,整体而言不稳定区域相对较大。

当参数F分别为0.45、1.4和3.5,其他参数保持基本参数不变时,幅频曲线变化图,如图7所示。幅值随F的增大而增大,解的多值性逐渐消失,不稳定区域随F的增大逐渐减小,当F达到一定值时,系统幅频曲线不再发生跳跃现象,因此,可通过加大F来抑制系统不稳定区域的产生,但会放大系统的幅值。

然而共振区域的大小并不都会随参数的变化而变化,如图8所示。阻尼比ξ(ξ=0.007、0.02和0.5)的变化对共振区域大小的影响较小,但多值区非共振支稳定,共振峰左移且共振频率减小。

综上所述可得,随参数的变化,在多值区,如果跳跃现象存在,则稳定共振解、不稳定解和不稳定非共振解一定存在，ξ变化除外。κ1的增大会使闭合曲线逐渐形成,然而其余参数增大闭合曲线消失。共振区域随κ2、χ1、χ2、α和F的减小而减小。共振峰因κ1和κ2的增大而右移且共振频率增大其余参数的变化规律则相反。除κ1影响外曲线的弯曲程度均减小。振幅会随着其它参数的增大而减小，f影响除外。因此,在实际应用中,可通过增大其它参数减小激励幅值来抑制共振峰峰值,但要避开跳跃点和不稳定状态。

5 力传递率

如果振源是被隔振物体本身,在隔振的研究中常常用通过隔振装置传递到基础上力的幅值与作用于振动系统上激励力的幅值之比,即力传递率Tf,来验证隔振系统对动态力的消减程度。在这里频率比小于共振频率比的区域称为低频区,频率比大于共振频率比的区域称为高频区。

下面分析系统的隔振效果。由式(1)和式(5)可得,传递到基础上的动荷载为

μ2K1(α)x(t)=K(α)x(t)-[C(α)-μc1x2(t)-

(24)

由于高次谐波分量对力传递率的影响很小[32],因此,这里只考虑频率为ω的力传递率,则

f(t)=f0cos(φ+φ)

(25)

其中

(26a)

(26b)

因此,力的传递率为

(27)

隔振器参数合理的选择既可使传递到基础上的力最小,也是降低振动传递的关键。当振子处于非线性振动时,分别以非线性刚度系数k1、分数阶项系数k2、非线性参数χ1和χ2、分数阶阶次α、激励幅值F、阻尼比ξ、频率比ζ为设计变量。将图2～8的数据代入式(22)和式(27)中得到不同设计参数影响下力传递率Tf与频率比ζ之间的关系图,如图9～15所示。从图9～15可得,力传递率从初始值1开始逐渐增大,达到共振频率时,产生共振峰,力传递率达到最大值,然后再逐渐减小。力传递率Tf>1时,系统不发生隔振作用,会使振动放大,若Tf<1,则说明产生隔振效果,该区域为隔振区,在隔振区Tf的值越小,隔振效果越好。

取与图2完全相同的参数,得到力传递率Tf与非线性刚度系数k1的关系,如图9所示,随着k1的减小,共振频率朝低频方向移动,在高频隔振区相同频率对应的力传递率值也变小。因此,减小刚度k1有利于提高隔振效果和增大有效隔振频率范围。根据k1与质量m、线性刚度k、系统(1)的非线性刚度μ1的关系可得,在其它参数不变的情况下减小m或μ1,增大k同样能提高隔振效果和增大有效隔振频率范围。

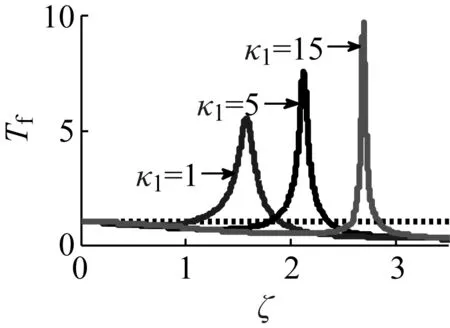
图9 非线性刚度系数κ1对 力传递率的影响

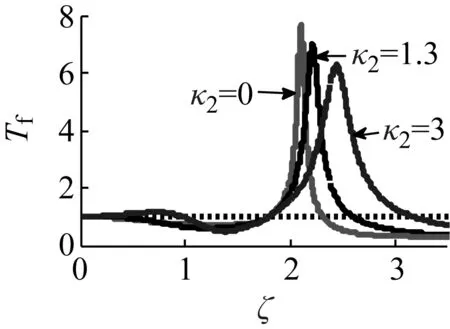
图10 分数阶项系数κ2对 力传递率的影响

图11 参数χ1对力传递 率的影响

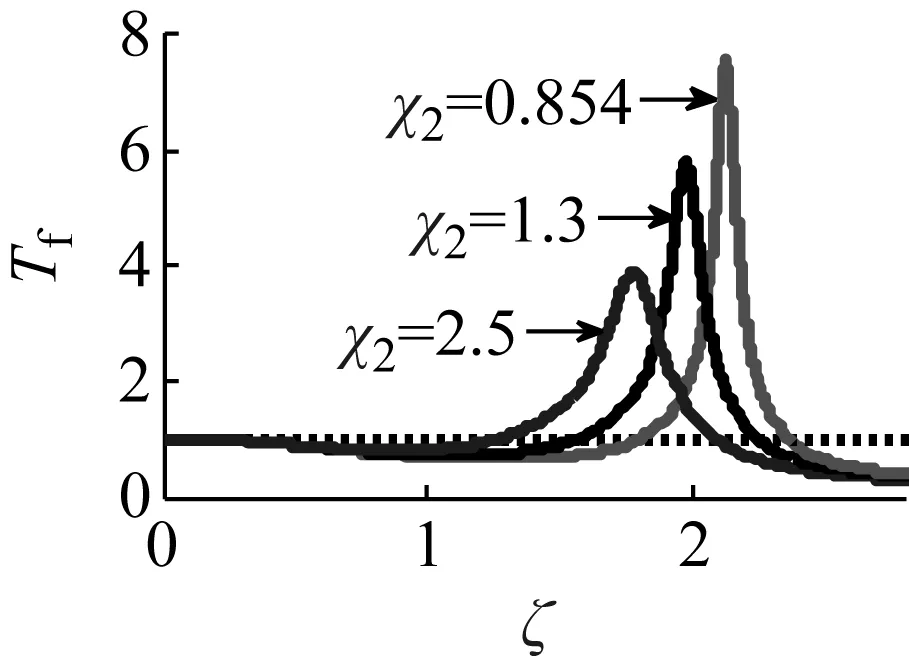
图12 参数χ2对力传递 率的影响

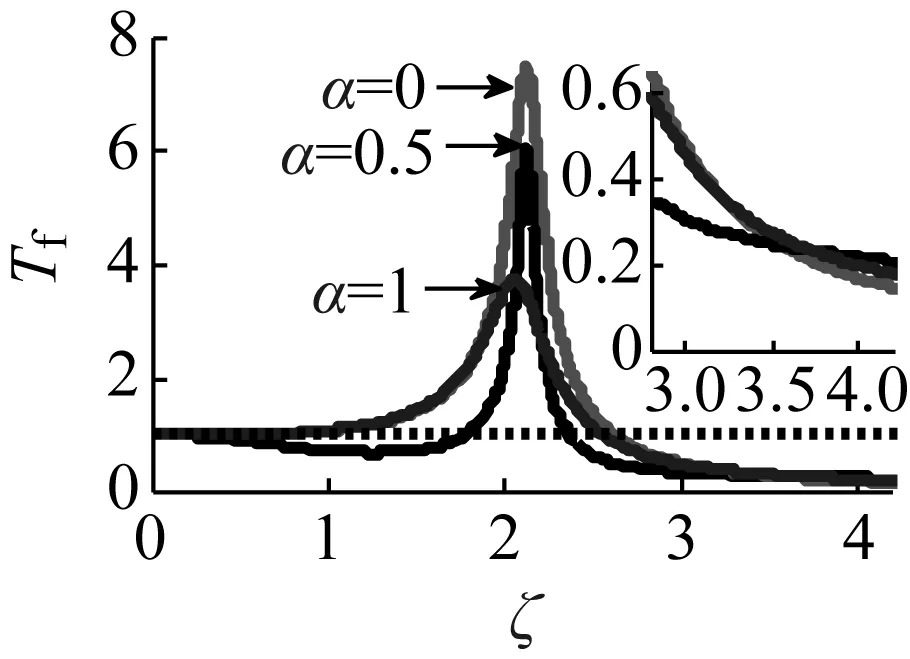
图13 分数阶阶次α对力传递率的影响Fig.13 Influence of fractional order α on force transmissibility

图14 激励幅值F对力传递率的影响Fig.14 Influence of amplitude F on force transmissibility

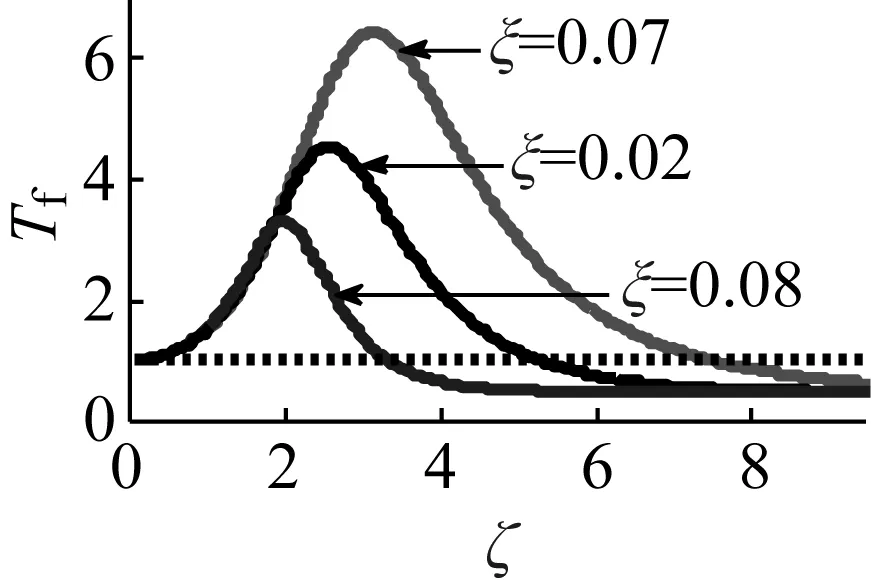
图15 阻尼比ξ对力传递率的影响Fig.15 Influence of damping ratio ξ on force transmissibility

改变分数阶项系数k2,将图3的参数代入式(22)和(27)中计算Tf,得到图10所示关系。由图10可得,增大k2,共振频率朝高频方向移动,共振峰峰值减小,在高频隔振区相同频率对应的力传递率值也变大,这说明k2在一定程度上会抑制共振峰和传递率。因而增大k2不利于提高隔振效果,也即其他参数不变,减小μ1或增大m对隔振效果有促进作用。

选取与图4和图5相同的参数,给出非线性参数χ1和χ2影响下的力传递率Tf与频率比ζ的关系图,如图11和12所示,随着χ1和χ2的增大,共振峰峰值减小,共振频率朝低频方向移动,高频隔振区对应的频率比减小,因此,产生隔振的频率范围变大。低频隔振区χ1、χ2越小隔振效果越好,高频隔振区相同频率对应的力传递率随χ1和χ2的增加而变小,也即增大χ1和χ2的值有助于提高隔振效果。考虑系统(1)中的参数,在其它参数不变时,增加c1和c2,或者增大m、减小k对提高隔振效果抑制共振峰有一定的帮助。

改变分数阶阶次α,取图6的参数得到不同α对应的力传递率,如图13所示。由图13可得,随着α的增大,共振峰峰值减小,低频隔振区α=0.5时隔振效果最好,高频隔振区较短频率比范围内α=0.5时隔振效果最好,过大频率范围内增大α会不利于隔振效果的提高。因此,增大α有利于抑制共振峰,但在大频率范围内不利于增强高频隔振区的隔振效果。

选取与图7相同的参数考虑F对力传递率的影响,如图14所示。由图14可得,与F对幅频曲线的影响不同的是随着F的增大,共振峰时Tf减小,低频隔振区F越小隔振效果越好,高频隔振区当频率比超过一定值后F越大Tf变小隔振效果越好,考虑到F与m的关系,在系统(1)中,低频隔振区增大m,高频隔振区减小m在一定程度上能提高隔振效果。

参考图8的参数,变化阻尼比ξ的值,得到不同阻尼比对应的力传递率,如图15所示。由图15可得,随着隔振器阻尼比ξ增大,共振峰时力传递率明显减小,共振频率朝低频方向移动,高频隔振区对应的频率比减小,因此,产生隔振的频率范围变大。但在低频区,系统不起隔振作用。高频隔振区阻尼比ξ越大Tf变小隔振效果越好,因此,与阻尼比ξ对幅频曲线的影响一样,增大阻尼比ξ能有效抑制共振峰,但阻尼比对低频区的力传递率没有影响,对共振区和高频隔振区的力传递率有影响,阻尼比越大力传递率越小。考虑系统(1)其他参数不变的情况下,增大μ或减小m、k在高频隔振区能提高隔振效果。

总之,在低频隔振区χ1、χ2和F越小隔振效果越好,ξ对力传递率的影响几乎可以忽略。共振区除κ1的影响外,只改变其它参数中的一个,增大参数均能抑制共振峰时的力传递率,特别地,随ξ、α、χ1和χ2的增加,共振频率朝低频方向移动,高频隔振区对应的频率比减小,这说明产生隔振的频率范围变大,然而随κ1、κ2和F的增加,共振频率朝低高频方向移动,共振频率比增大,高频隔振区对应的频率比增大,说明有效隔振频率范围变小。在高频隔振区相同频率对应的力传递率随ξ、χ1和χ2的增加而变小,F变化时当频率比达到一定值后也有相同规律,但增大κ1、κ2结果明显相反,因此,增大ξ、χ1、χ2和F的值,减小κ1、κ2的值有利于提高隔振效果。

6 结 论

本文用平均法给出了改进的分数阶 van der Pol-Duffing 隔振振子的主共振响应,在此基础上计算了力传递率,进一步分析了不同参数对幅频曲线和力传递率的影响,为该类隔振振子的设计和应用提供一定的参考。主要结论如下

(1) 将数值解与解析解进行比较,发现其结果吻合良好,证明了解析解的正确性。

(2) 分析了无量纲化后非线性刚度系数、分数阶项系数、非线性参数、分数阶阶次、激励幅值和阻尼比对幅频曲线的影响。结果表明,解的稳定性、解的个数、共振区域、共振频率、跳跃性、弯曲程度、共振峰峰值均受这些参数的影响,且除激励幅值影响外,共振峰峰值随其它参数的增大而减小,也即增大其它参数可达到抑制共振峰峰值的目的。

(3) 在幅频曲线的基础上,进一步讨论了不同频率区段的力传递率受非线性刚度系数、分数阶项系数、非线性参数、分数阶阶次、激励幅值和阻尼比的影响。结果发现,在低频隔振区,非线性参数和激励幅值对隔振效果的影响十分明显,阻尼比对隔振效果影响不大。在共振区,除非线性刚度系数外其它参数均抑制力传递率的峰值且随阻尼比、分数阶阶次和非线性参数的增加,共振峰逐渐向频率比减小方向移动,共振频率比减小。在高频隔振区,阻尼比、分数阶阶次和非线性参数的增大在一定频率比范围内有利于扩大有效隔振频率范围,增大阻尼比,非线性参数和激励幅值的值减小非线性刚度系数,分数阶项系数的值有助于提高隔振效果。本文的研究过程和结果对于多自由度类似系统的稳态解或者单自由度类似系统的瞬态响应分析具有一定的借鉴价值。