基于区间数TOPSIS法的绿色工艺方案决策

周 涛，汪永超，李汶俊，张栩静，毛凯宁

(四川大学机械工程学院，成都 610065)

0 引言

制造业是国民经济持续发展的基础产业，而机械加工是制造业中的一个关键环节，工艺方案的优劣会对生产成本、生产效率和产品质量造成显著的影响。同时，环境污染和资源紧缺等问题引发出加工工艺的绿色性需求，原料使用率和废料废气的排放量也成为衡量工艺方案优劣的衡量指标。所以，对加工工艺方案的绿色决策，具有重要的理论和实际意义。

目前，加工工艺方案决策的方法主要有遗传算法、层次分析法、熵权法以及逼近理想排序法等。郭继通等[1]针对研磨抛光加工的工艺选择问题，提出基于遗传算法和神经网络的加工工艺参数决策方法；丛成[2]从加工工艺考察指标出发，提出基于层次分析法的加工工艺评价方法；韩自强等[3]根据绿色制造的要求，提出基于熵权TOPSIS法的机械加工绿色工艺方案决策。

但是，这些方法不能在保证工艺方案绿色性的同时解决决策者的主观偏好和加工过程中复杂的干扰因素导致的决策结果的偏差。针对这些问题，本文利用绿色制造决策体系，结合模糊层次分析法和逼近理想排序法构建决策模型，并且运用区间数代替点值进行运算，消除评价者主观判断的偏好和加工过程不确定性的影响。

1 建立绿色制造决策指标体系

近年来智能化、绿色化、高效化以及低耗化成为制造产业的革新方向。科学的决策指标体系能够保证工艺方案符合上述革新方向的要求。

参考绿色制造决策框架模型[4]，对工艺过程中的生产时间、生产成本、产品质量、环境影响和资源消耗这5个绿色制造指标[5]进行分析，建立加工工艺决策指标体系，如图1所示。

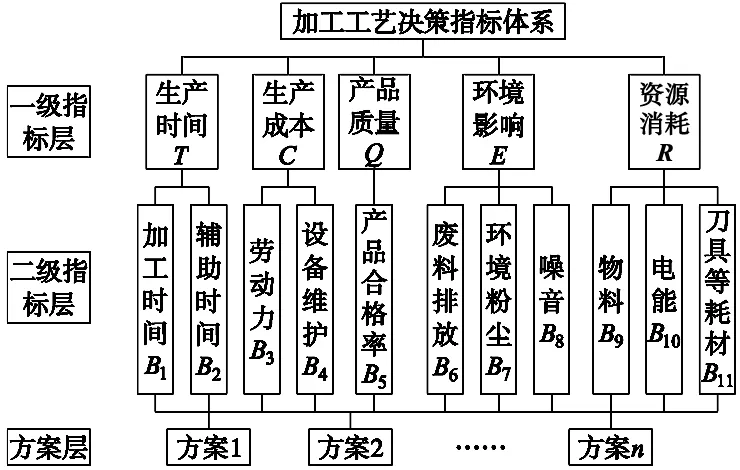
图1 加工工艺决策指标体系

2 建立加工工艺决策模型

2.1 构建模糊判断矩阵

模糊判断矩阵是根据选取的模糊标度值，比较各指标的相对重要性，得到由评分值所构成的矩阵[6]。

构建出的模糊判断矩阵A为：

(1)

其中，aij为指标i相对于指标j的重要程度。并且，模糊判断矩阵A满足：

(2)

由式(2)可知，矩阵是一个模糊互补矩阵。

考虑到模糊判断矩阵的一致性要求，采取0.1～0.9的模糊标度法[7]。

2.2 构建模糊一致性矩阵

准确可靠的权重值依赖于模糊判断矩阵的一致性。模糊一致性矩阵分为加型和积型，类型与模糊标度的选取有关[8]，0.1～0.9标度属于加型标度。

对A处理后得到模糊一致矩阵R为：

(3)

其中，

(4)

式中，

2.3 计算权重向量

在模糊层次分析法的权重计算中，普遍运用最小二乘法计算权重向量[9]。

2.3.1 层次单排序

层次单排序是指某一个一级指标的二级指标的重要程度排序。

得到模糊一致性矩阵R后，通过最小二乘法计算出各指标的权重为：

(5)

权重向量w为：

w=[w1,w2,…,wn]

(6)

2.3.2 层次总排序

层次总排序就是最底层各指标的重要程度排序。根据式(5)，可以得到第i层的指标权重向量为：

wi=[wi1,wi2,…,win]i=1,2,…,l

(7)

其中，l为层次总数。

则最底层指标的总权重W为：

（2）提高国库集中支付效率。《国务院关于印发2016年推进简政放权放管结合优化服务改革工作要点的通知》提出了“优化政府服务，提高办事效率”的具体要求。财政部门应该进一步结合高校实际，改革国库集中支付，在安全的前提下开放国库支付的端口，允许高校网银系统对接，提高财政专项的支付效率。

W=w1×w2×…×wn

(8)

2.4 构建区间数决策矩阵

根据专家团队对决策指标数值的估计，建立具有区间数[10]形式的决策矩阵[11]。

区间数决策矩阵X为：

(9)

其中，xij为第i个方案的第j个指标的区间数值。

(10)

2.5 标准化区间数决策矩阵

由于各指标的数量级和量纲不同，故要进行区间数决策矩阵的标准化[12]。

标准化区间数决策矩阵S为：

(11)

其中，

(12)

对于效益型指标：

(13)

(14)

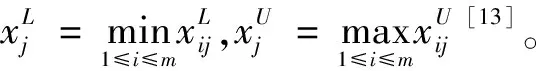
(15)

由此，可以得到再标准化区间数决策矩阵F为：

F=[fij]m×n

(16)

2.6 构造加权标准化区间数决策矩阵

加权标准化区间数决策矩阵V为：

V=[vij]m×n

(17)

其中，vij=fij×wj。

2.7 确定正、负理想解

正理想解是指每一指标中选出的最大评估值的集合，而负理想解则相反[14]。

正、负理想解分别为：

(18)

(19)

其中，I′为效益型指标；I′′为成本型指标。

2.8 计算各方案与理想解的距离和

各备选方案与正、负理想解的距离分别为：

(20)

(21)

各方案与理想解的接近度为：

(22)

其中，Ci越大，相应的方案越接近于理想解，那么就可以根据Ci的大小选择出最优方案。

3 应用实例分析

为了验证决策方法的实用性，以某车间中间轴齿轮生产为例，综合考虑设备设施、加工方法、加工流程、物料选用等问题，提出了3种加工工艺方案。现在运用上述决策方法选出最优方案。

按照中间轴齿轮生产的实际要求，以及专家团队对一级指标相对重要性的判断，建立模糊判断矩阵A：

根据式(4)，计算出模糊一致性矩阵R：

根据式(5)，计算出各指标对应的权重，得到一级指标的权重向量w1为：

w1=(0.1875,0.2063,0.2375,0.1875,0.1813)

对于每个一级指标的二级指标，同样由专家团队根据0.1-0.9模糊标度法给出其二级指标模糊判断矩阵。根据式(1)～式(6)，可以计算出各二级指标的权重w2。

根据式(8)，计算出二级指标的总权重W，如表1所示。

表1 二级指标总权重

对3种工艺方案进行详细分析和实际考察后，确定决策矩阵的各项区间数，如表2所示。

表2 决策指标区间数值

根据表2的数据以及式(9)、式(10)，可以得到指标区间数决策矩阵X。

根据式(11)～式(16)，对区间数决策矩阵X进行标准化，得到标准化区间数决策矩阵S。

根据式(17)，计算出加权标准化区间数决策矩阵V。

根据式(18)和式(19)，得到11个决策指标的正、负理想解，如表3所示。

表3 各决策指标的正、负理想解

根据式(20)和式(21)，计算出各方案与正、负理想解的距离，如表4所示。

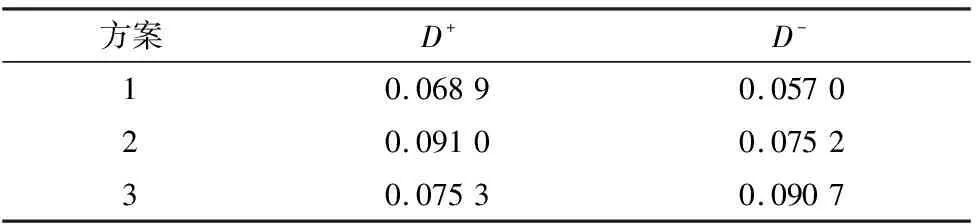
表4 各方案与正、负理想解的距离

根据式(22)，计算出各方案与理想解的接近度，如表5所示。

表5 各方案与理想解的接近度

根据表5可知，C3>C1>C2，所以方案3最优，其次是方案1，最后是方案2。

4 结束语

为了在实际生产中快速精准地确定加工工艺方案，提出了一种基于区间数逼近理想排序法的绿色工艺方案决策方法。该方法以绿色制造指标体系为基础，构建绿色加工工艺决策体系，确保了工艺方案的绿色性，减少环境影响和资源消耗。在逼近理想排序法的基础上，运用区间数对评价指标进行量化，消除了复杂加工过程中不确定因素的影响，并且更加符合人们对模糊事物的认识习惯。该方法为加工工艺方案的选择提供了新思路，让工艺方案决策更加准确和高效。最后，通过实例分析证明了该决策方法的实用性和科学性。