基于PCA和SVM的微铣刀磨损状态识别*
2022-01-27彭明松王二化
彭明松,王二化,张 屹
(1.常州大学机械与轨道交通学院,常州 213164;2.常州信息职业技术学院常州市高端制造装备智能化技术重点实验室,常州 213164)
0 引言
随着微铣刀的不断投入使用,刀具磨损量也就逐渐变大,加工方式、工件材料等都对磨损速度产生了很大的影响。加工过程中磨损现象也基本可以划分为3~4个磨损阶段,每个阶段呈现一定的规律与特性。刀具磨损程度的大小将直接影响切削过程中产生的信号。切削产生的信号带有丰富的刀具磨损信息,所以分析刀具磨损与其之间的关系,从切削信号中提取能够反映刀具磨损的特征是间接研究刀具磨损监测的关键。
李光辉[1]运用GA-BP神经网络识别旋转超声加工刀具状态,准确率显著提升。BINSAEID等[2]采用径向基神经网络,对刀具磨损状态进行了预测,得到的辨识精度也较高。谢庆陆等[3]在研究变参数铣削刀具状态监测时,引入了无量纲切削力时域特征,将旧特征和新特征分别输入SVM模型中。LI等[4]用v-SVM监测刀具监测刀具状态,提取了14个相关特征,通过分析也提高了准确率。刘宇[5]对采集到的切削力信号进行了时域、频域和时频的多重分析和特征提取,对提取的大量特征分析之后,提出各方向特征量比值法,最后组成特征向量输入多分类支持向量机模型中进行模式识别,通过实验验证更适用于刀具监测。刘同瞬[6]通过分析磨损对切削信号的影响,从切削信号中提取了能够反映微铣刀磨损的信息,进而分析了微铣削刀具磨损的变化规律,并综合提取出来的磨损特征和刀具磨损的变化规律,提高了微铣削刀具磨损的准确性。
基于此,为了提高刀具磨损状态的识别度,本文提出了一种能够有效识别微铣刀磨损状态的方法。通过花朵授粉优化算法,对SVM的模型参数寻优,提升了模型的识别性能和计算效率,和其它优化算法相比,花朵授粉优化算法也具备较大的优势,因此该方法应用于刀具磨损状态监测具有实用价值。
1 实验方法
微铣刀的刀具直径通常在1 mm以下,本文所用的微铣刀是直径0.5 mm的钨钢硬质合金。选用型号为1A314E的IEPE压电式三向加速度传感器,并通过型号为DN5902N数据采集系统采集微铣刀发生磨损时的振动信号。根据设定的参数,在实验装置上进行模具钢零件的平面铣削,同时采集主轴部件的振动加速度信号,每隔3 min,停机,拆下刀具,总共停机5次,所以总共有5种磨损状态,分别为:初始磨损、轻度磨损、中度磨损、严重磨损、刀具失效,由于刀具失效状态,刀具磨损程度过深,所以本文将微铣刀磨损类别分为4个级别。为了获取更加全面的加速度信息,两个加速度传感器分别安装在主轴的x和y轴方向,采样频率为5000 Hz。实验装置如图1所示。

图1 信号采集实验装置
2 信号分析
基于上述铣削实验装置,可以得到振动发生过程中的z轴方向上的加速度信号,如图2所示。
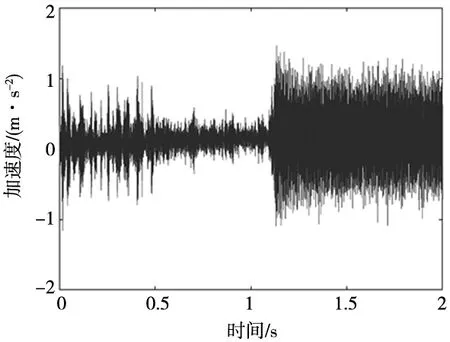
图2 加速度信号波形图
前半段表示未铣削时的状态,后半段表示发生铣削时的状态。横坐标表示的振动信号采集时间,纵坐标表示的是刀具振动加速度值。
对实验采集到的振动信号进行时域分析,提取均值、均方根等10个时域特征。但是仅通过时域分析法反映出的刀具磨损信息是有限的,且时域分析只能反映出随着刀具磨损情况变化振动和力信号幅值的变化,而实际信号中包含多种频段信息,还与频率、相位等信息变化相关。因此需要通过频域分析法来进一步提取特征值。频域特征提取首先对信号进行快速傅里叶变换,在频域范围内揭示信号内在频率特性以及信号时间特性与其频率特性之间的密切关系。对Z方向的振动信号进行傅里叶变换,得到如图3~图6所示的振动信号的频域图。

图3 初始磨损振动信号频域图 图4 轻度磨损振动信号频域图

图5 中度磨损振动信号频域图 图6 严重磨损振动信号频域图
通过对4种不同状态的Z方向振动信号频域图的分析,振动信号在500~1000 Hz这个区域可以大概看出,随着磨损量的增加,磨损程度的加剧,频谱的幅值也有一定程度的提升。用MATLAB进行编程处理,提取频域均方根、频域偏态等10个频域特征值用于接下来的模型输入。
3 微铣刀振动信号的识别
3.1 特征降维
尽管已经提取了10个时域特征和10个频域特征,但是信号处理后提取的时域特征和频域特征存在冗余特征并且维数相对较高,这会对后期所用的刀具状态识别的模型训练速度与识别度造成较大的影响。因此,需要经过适当的计算对上述的多个特征进行降维,本文应用PCA对提取的特征进行信息融合,再以融合后的特征向量作为支持向量机的样本输入。对实验采集到的1000组振动信号以及提取的10个时域特征和10个频域特征组合成一个1000行20列的矩阵M,具体组合方式如式(1)所示:
(1)
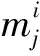
再将所建立的特征矩阵M用向量形式表示,如式(2)所示:
M=[m1m2…mb]
(2)
各个列向量的平均值如式(3)所示:
(3)
然后用协方差计算数据样本,如式(4)所示:
(4)
要想得到能代表大部分信号特征的主成分,需要对协方差Cov(M)进行特征分解,进而可以得到新的特征矩阵N和特征值,λ1,λ2,…,λk,前k阶特征值对应的特征向量就是主成分,而主成分组成的新矩阵Nk=(u1,u2,…,uk)就是振动信号数据的PCA分析结果。如此,不仅降低了特征维度,也减少了许多冗余特征。
3.2 支持向量机
根据众多实验和实践表明,影响支持向量机(support vector machine,SVM)[7-9]性能好坏的因素主要有三种类型,他们分别是核函数的类型、核函数参数g和惩罚系数C。因此,选择合适的SVM参数对支持向量机模型有着很重要的实际意义。对于训练样本集:
(x1,y1),(x2,y2),…,(xN,yN),x∈Rn,y∈{-1,1}
最优分类超平面的二次规划问题为:
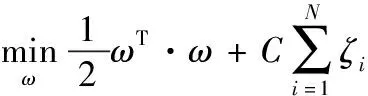
s.t.yi(ωTxi+b)≥1-ζi,ζi≥0,i=1,2,…,N
(5)
其Lagrange函数为:
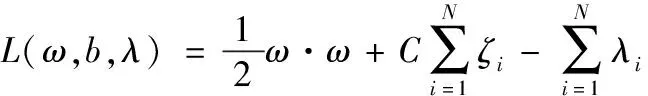
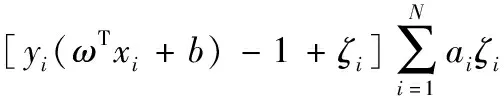
(6)
其中,λi≥0,i=1,2,…,N。其对偶问题为:
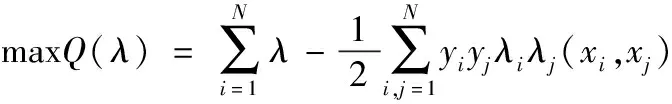

(7)
最终得到的决策函数为:
(8)
对于线性不可分问题的对偶函数则为:


(9)
其中,Φxi×Φxj=K(xi,xj)即为核函数,相应决策函数为:
(10)
采用不同的核函数会生成不同的支持向量机分类器。由于在RBF中只需确定一个参数(即参数g),在优化过程中,更利于获得更好的参数,所以本文选择高斯核函数作为SVM的核函数。高斯核函数:
(11)
惩罚系数C的用途是控制模型复杂度和逼近误差的折衷,选取的C的值越合适,对数据的拟合程度就越高,此外,高斯核函数值g对模型的分类精度也有重要影响,所以要获取支持向量机的优越性能,需要选取合适的C及g。
3.3 基于花朵授粉算法优化SVM模型
从达尔文进化论可知,经过大自然各种复杂环境条件的挑选,花朵通过外力进行授粉繁衍,最终保留下能更好适应目前环境的的最优机制。通过简化自然界中花朵授粉的原理,花朵授粉算法[10-12]的基本原理和优化SVM的流程图如图7和图8所示。
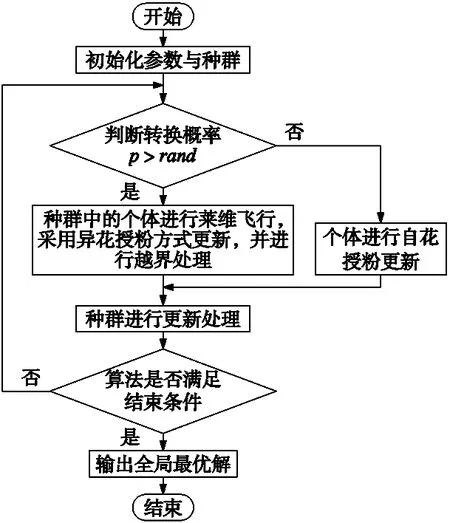
图7 花朵授粉算法基本原理的流程图
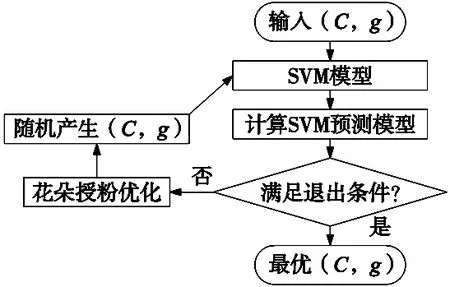
图8 花朵授粉算法优化SVM的流程图
花朵授粉算法(flower pollination algorithm,FPA)的具体流程如下:
确定一个目标函数:f(x),x=(x1,x2,…,xk),为了在初始种群中找到全局最优解d,需要初始化种群。将图7中的转换概率p的范围设置为[0,1],并设置最大迭代次数。
While (s<最大迭代次数)
Fori=1:n(种群中全部的n个花粉)
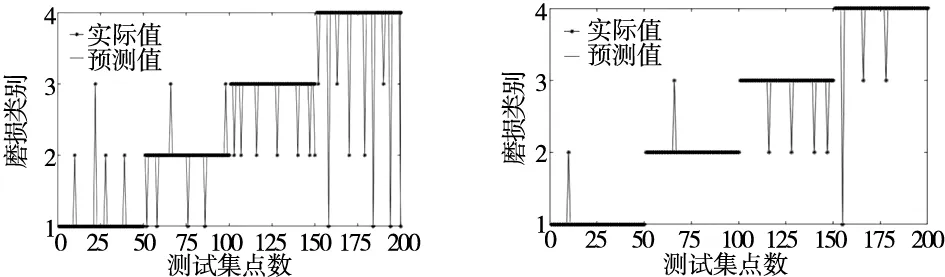
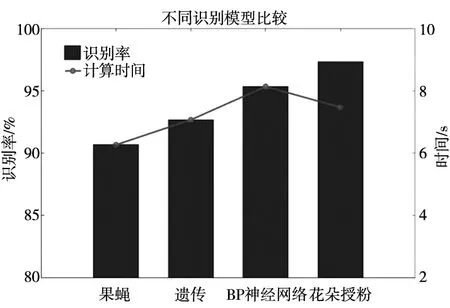
If rand Else 局部搜索 End if评测新解,若新解好,继续在种群中更新 End for找出当前最优解 End while输出找到的最优解组合(C,g) 在全局搜索过程中,授粉者通过Lvey的这种飞行机制进行下一步探索,所以L是和授粉强度密切相关的参数,L可用式(12)表示: (12) 其中,Γ(λ)是标准的伽马函数。 接下来通过FPA算法寻找SVM的惩罚系数C和RBF核函数参数g的组合变量(C,g)的最优对象,直至算法停止,输出使SVM模型分类识别率最高的最优组合解。 本文将铣刀的磨损程度分为4类,以特征降维后的特征数据为基础,取出一定量的数据,按照一定的比例来划分训练集和测试集。以PCA降维后的特征作为SVM模型的输入,最终的识别结果如图9和图10所示。 图9 SVM模型识别结果 图10 花朵授粉优化SVM模型识别结果 从图9和图10可以看出,特征降维后SVM模型的总体识别率也比较高,达到了87%。但是经过花朵授粉算法对惩罚系数C和RBF核函数参数g寻优后,优化参数后的模型的总体识别率有了明显的提升,达到了95.5%。并且各个磨损状态的识别率也有不同程度的提升。 为了进一步验证本文提出的方法具备优势,将计算结果与果蝇算法优化、遗传算法优化和BP神经网络进行对比,结果如图11所示。 图11 不同识别模型的比较 和其它分类算法相比,虽然计算时间仅低于BP神经网络,但是本文的花朵授粉算法优化SVM模型在识别率方面具备明显优势。说明引入的花朵授粉优化算法在提高分类精度的同时,算法效率也相对较高。 本文结合花朵授粉优化算法,对SVM模型的惩罚系数C和RBF核函数的参数g进行寻优。避免了起初SVM参数选择的不合适而带来的局部最优和过拟合的问题。对实测样本的分析结果表明,微铣刀磨损的振动信号可以用于刀具磨损状态的有效识别,花朵授粉算法优化SVM模型后,花朵授粉优化算法可以在特征向量的偶然性与确定性之间找到一个更好的平衡点,从而避免较大的随机性所带来的低效的搜索效率以及较低的收敛速度等问题。在分类识别和算法效率方面具有综合优势,和其它优化模型相比,也有更好的学习能力和泛化能力,具备一定的实践意义和理论价值。
4 结论
