基于模型线性自抗扰的PMLSM位置控制

熊东海

(惠州城市职业学院机电学院，惠州 516000)

0 引言

永磁直线同步电机(Permanent magnet linear synchronous motor，PMLSM)由于采用直接驱动的方式，具有效率高、推力大、响应速度快等特点，在精密加工、半导体封装、视觉检测等各种精密运动领域得到了广泛应用[1-3]。从工程控制的角度看，PMLSM由于没有了中间传动机构，使得在实际运行中受到的推力波动、导轨摩擦力变化以及负载阻力等扰动将直接作用在PMLSM动子上，影响位置控制精度，增加了抗扰动控制难度[4-5]。

目前，大多PMLSM运动控制系统仍采用传统的PID控制策略[6]。PID控制不依赖被控对象的模型，具有较强的适应性，但是存在“快速性”与“超调”的矛盾，且参数整定往往依赖工程经验，对扰动的抑制能力差，不适合用于PMLSM伺服系统的快速准确控制。为了弥补传统PID控制的不足，一些现代控制理论方法被尝试用于PMLSM伺服控制系统，并取得了一定的成果，如模糊控制[7]、滑模控制[8]、迭代学习控制[9]、神经网络控制[10]等。这类方法通常需要建立被控对象的精确数学模型，但由于PMLSM本身存在多变量、强非线性、强耦合的特征，获得精确的模型将十分困难，限制了其在工程中的应用。

自抗扰控制(active disturbance rejection control，ADRC)技术不依赖被控对象精确的数学模型，将建模误差、内部不确定性以及外部扰动统一为总扰动，通过扩张状态观测器进行实时观测，并在状态反馈控制律中对总扰动进行动态补偿，具有极强的抗扰动能力[11]。传统的ADRC采用非线性调节函数，控制参数多且难以整定。为此，学者们提出了许多改进算法，并取得了良好控制效果[12-15]。其中，GAO[12]提出的线性ADRC(linear ADRC，LADRC)结构，将控制参数减小为3个，大大方便了工程实践。

本文以PMLSM伺服系统为研究对象，提出了一种基于已知模型信息的线性自抗扰控制(model-based LADRC，MLADRC)算法。区别于传统的线性自抗扰控制策略，该方法中设计的模型线性状态扩张观测器，能够降低对未知总扰动的观测负担，提高对系统各阶状态的观测精度；引入加速度前馈的改进线性状态反馈控制律，以位置观测信号作为反馈输入，避免了速度观测信号的相位滞后影响，进一步提高了PMLSM伺服系统的动态响应性能和抗干扰能力。

1 PMLSM伺服系统建模

通过坐标变换，得到PMLSM在d-q轴下的数学模型为：

(1)

式中，R为初级电阻；id、iq为d、q轴电流；ud、uq为d、q轴电压；Ld、Lq为d、q轴电感；ψPM为定子永磁体磁链；v为动子运动速度；τ为极距；np为极对数；Fe为电磁推力。

驱动器采用矢量控制方式，d轴的参考电流信号id=0。由于直线电机气隙较大，近似认为d轴和q轴的定子电感相同，即Ld=Lq=L。于是电磁推力方程可重写为：

Fe=Kfiq

(2)

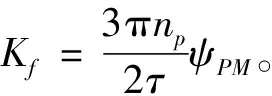
iq=kqu

(3)

式中，kq为缩放比例。PMLSM伺服系统的机械运动方程可表示为：

(4)

式中，Mv为电机运动质量；Bv为电机粘滞摩擦系数；Fd为外部扰动阻力；y为电机输出位移。

结合式(2)～式(4)，忽略外部扰动阻力的影响，可得PMLSM伺服系统从输入电压到输出位移的传递函数表达式为：

(5)

式中，a=Bv/Mv；b=kqKf/Mv，其模型参数通过系统辨识获得。而系统在实际运行中，除存在外部扰动阻力外，推力波动、未建模动态以及反馈回路的测量噪声均不可避免。为得到简化的PMLSM伺服系统控制模型，将所有的不确定项归为未知总扰动du。于是得到最终控制模型的微分方程为：

(6)

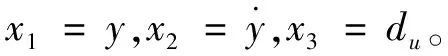
(7)

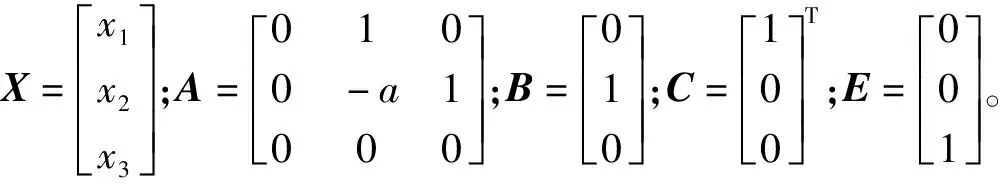
2 基于模型的线性自抗扰控制器设计

2.1 模型线性扩张状态观测器设计

根据式(7)设计基于模型的线性扩张状态观测器(model-based linear extended state observer，MLESO)，其表达式为：

(8)

式中，b0为b的估计值；A、B、C同式(7)；Z=[z1z2z3]T为系统X的观测状态；L=[l1l2l3]T为观测增益参数。式(8)的特征多项式为：

λ1(s)=s3+(l1+a)s2+(l2+l1a)s+l3

(9)

根据极点配置原理[12]，将MLESO的极点配置在-wo处，即λ1(s)=(s+wo)3，得到关于观测增益参数的整定公式：

(10)

式中，wo为MLESO的观测带宽。

2.2 改进线性状态反馈控制律设计

由于观测器得到的系统观测状态相比实际状态必定存在一定的相位滞后，其中速度观测信号作为位置观测的信号的近似微分，其滞后问题可能更为严重。传统的LADRC在反馈控制律中利用目标指令信号、位置观测信号以及速度观测信号计算控制量，其控制律结构简单，易出现调节缓慢的问题[16]。本文结合已知的模型参数信息，设计一种只将位置观测信号作为反馈输入，并引入加速度前馈的改进线性状态反馈控制律(improved linear state feedback control law，ILSFCL)：

(11)

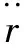
(12)

于是，通过在控制律中对未知总扰动的补偿，将被控对象改造成了积分串联形式，大大方便了控制器的设计。此时PMLSM伺服系统的闭环系统特征多项式为：

λ2(s)=s2+k2s+k1

(13)

根据极点配置原理，将闭环系统的极点配置在-wc处，即λ2(s)=(s+wc)2，于是，

(14)

式中，wc为ILSFCL的控制带宽。MLADRC的控制结构如图1所示。

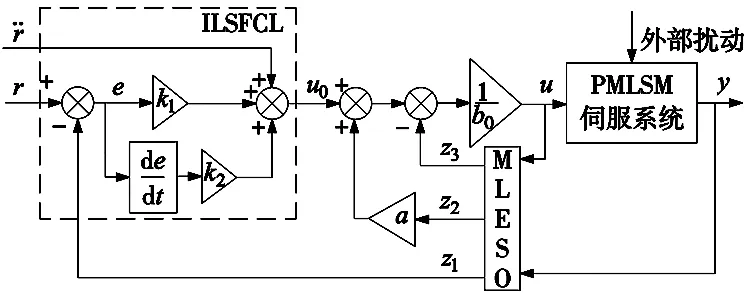
图1 MLADRC控制结构图

2.3 稳定性分析

定义跟踪误差：

εj=rj-xj,j=1,2

(15)

(16)

构建如下李雅普诺夫函数：

(17)

则至少存在一点ζ∈[0ε1]，使

(18)

同时：

(19)

3 仿真与实验分析

3.1 仿真分析

所采用的PMLSM参数如表1所示。通过系统辨识得到PMLSM伺服系统的模型信息参数为a=7.655，b=2.57。为验证MLADRC的可行性，利用Simulink设计MLADRC与PID和LADRC对比的位置响应仿真实验。

表1 电机参数

给定加速度为1g，速度为0.2 m/s和行程为10 mm的规划指令作为位置输入信号，并在2.5 s时加入幅值为-1 V的控制量常值扰动。LADRC与MLADRC选取相同的控制参数，并根据经验法对PID的控制参数进行整定，仿真曲线如图2所示。

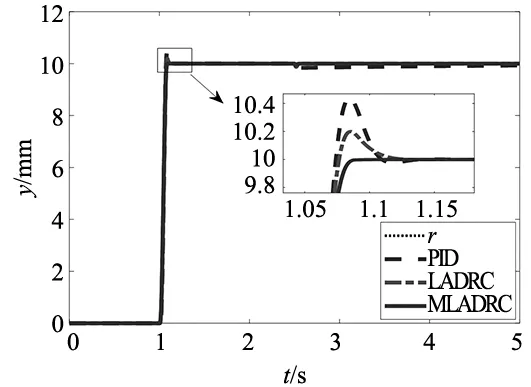
(a)位置响应曲线

由图2可知，PID控制到位时存在较大超调，对常值扰动的抑制能力弱。LADRC存在一定的超调，且稳定时间较长。而MLADRC几乎没有超调，稳定时间短，且对常值扰动的抑制更快。

3.2 实验验证

为验证MLADRC方法的实际控制性能，本文搭建了PMLSM伺服系统的实验装置，包括dSPACE控制器、Akribis驱动器、无刷无铁芯PMLSM、光栅尺、上位机等，控制系统示意图如图3所示。首先由光栅尺反馈信号给到驱动器进行电流环内环控制，然后由驱动器模拟出ABZ数字脉冲信号传输给dSPACE控制器进行位置信号解码，并在dSPACE中搭建位置闭环计算得到控制电压，输出给驱动器，最终驱动PMLSM运动。

图3 控制系统示意图

输入行程为10 mm、速度为0.2 m/s、加速度为1g的规划指令，如图4所示给出了不同控制方法下的动态响应情况。

图4 位置响应实验曲线

实验结果可见，PID的超调最大，为0.613 mm，稳定时间为64 ms。LADRC的超调较PID小，为0.151 mm，但稳定时间较PID长，为115 ms。而MLADRC的超调和稳定时间都最小，分别为0.005 mm和44 ms，其稳定时间较PID和LADRC分别减小了31.3%和61.7%。

为验证MLADRC对外部扰动的抑制能力，考虑两种不同扰动下的闭环响应。一种是在2.5 s时加入幅值为-1 V的常值扰动，另一种是在1 s～3 s区间加入幅值为0.25 V的正弦扰动，实验结果如图5所示，其最大扰动偏差和扰动误差的IAE指标列于表2。

(a)常值扰动实验图

表2 不同扰动作用下的性能指标

由图5和表2可见，对于常值扰动和正弦扰动，相比于PID和LADRC，MLADRC的最大扰动偏差和IAE均最小。其中，对于常值扰动的最大扰动偏差较PID减小了0.335 mm，较LADRC减小了0.174 mm；对于正弦扰动的最大扰动偏差较PID减小了0.006 mm，较LADRC减小了0.014 mm。这表明MLADRC具有良好的抗扰动能力，能够快速抑制不同形式下的外部扰动作用。

4 结论

针对摩擦力变化以及外部扰动等不确定性对PMLSM伺服系统位置控制精度的影响，本文提出了一种MLADRC算法。该方法设计了融合模型参数信息的模型线性扩张状态观测器，可有效降低对未知总扰动的观测负担，提高对系统各阶状态的观测精度。并通过引入加速度前馈的改进线性状态反馈控制律，提高了位置控制精度。实验结果证明：对于点位运动，所提方法可有效降低超调和稳定时间，其稳定时间相比于PID和LADRC分别减小了31.3%和61.7%；对于不同形式的外部扰动，所提方法具有快速的抑制能力。本文设计的MLADRC算法对提高PMLSM伺服系统的动态响应性能以及抗干扰能力具有较高的实用价值。