机械产品关键质量特性综合识别方法*

鞠萍华，许文林，谷豪东，冉 琰

(重庆大学机械传动国家重点实验室, 重庆 400044)

0 引言

机械产品质量特性众多，多个质量特性共同表征产品的质量[1]。关键质量特性识别是一个较为复杂和困难的问题，识别过程具有主观性、模糊性和随机性等不确定问题[2]。目前，国内外针对关键质量特性识别方法主要分为单一识别方法和组合识别两类。单一识别方法包括主观赋权和客观赋权，主观赋权大多是定性的方法，利用专家的经验主观判断给出质量特性的重要度，如专家组评判法、模糊层次分析法、模糊综合法等[3-4]；客观赋权方法通过收集或实验获取原始数据，根据各质量特性间的相关关系大小确定重要度，如信息熵、最小二乘法等[5-6]。单一识别方法往往仅从一个角度应用单一的理论方法获取权重值来提取关键质量特性，所获得的结果准确性具有一定的局限性。为了弥补单一识别方法的不足，组合识别方法大大提高了的关键质量特性识别的准确性，如QFD与FMECA组合方法[7]、模糊AHP与信息熵[2]组合方法等。

综上所述，关键质量特性识别方法主要存在两个方面的问题：一是质量特性识别方法多是笼统的对产品所有质量特性分析权重进行排序，没有考虑质量特性的层次性；二是质量特性属性通过专家打分经过模糊处理后仍不能避免主观性的影响，且缺少定量提取过程。可拓层次分析法(extension analytic hierarchy process,EAHP)在层次分析法的基础上能有效避免专家主观性而带来的误差且无需进行一致性检验[8]；信息熵充分挖掘数据潜在的信息并尽可能的减少人工因素的干扰，使结果更加客观有效[5]；模糊Borda法考虑了各方法得分差异以及排序中位次两方面的因素，在组合提取和评价方面有较好的效果[9]。基于此，本文在机械产品质量特性层次分析的基础上提出综合可拓层次分析法和信息熵法的模糊Borda法机械产品关键质量特性综合识别方法，提高关键质量特性识别的准确性。

1 机械产品质量特性层次分析

1.1 机械产品质量特性层次模型

机械产品质量特性众多，为解决机械产品质量特性层次混乱，对机械产品质量特性从宏观尺度、中观尺度、微观尺度进行分层[10]，建立如图1所示质量特性层次模型。

图1 机械产品质量特性层次模型

(1)质量目标层。质量目标层反映机械产品整体质量水平，是所有质量特性水平的综合，其度量指标为质量特性综合满意度。

(2)一级质量特性层。一级质量特性层是行业或领域所关注的质量特性，属于宏观尺度上的质量特性，其中某一质量特性可以作为质量目标评价产品的质量水平。例如性能、可信性、经济性、适应性、社会性。

(3)二级质量特性层。二级质量特性层是用户、企业及相关方所关注的质量特性，属于宏观尺度上的质量特性，是一级质量特性进一步分解。例如性能可分为精度、使用寿命、精度保持性、性能稳定性等；可信性又可分为可靠性、维修性和维修保障性等；适应性可分为工作平稳性、环境适应性、人机交互性、互换性等；经济性包括成本、技术先进性、经济效益等；社会性可分为可回收性、绿色性、安全性、环保性。二级关键质量特性层是机械产品质量控制的重点。

(4)指标层质量特性。指标层质量特性对应于中观尺度，是宏观质量特性进一步分解用于评估质量特性指标的集合，可用于评价二级质量特性，如通常用可靠度、平均故障间隔时间MTBF等指标来综合评价产品可靠性水平。

(5)微观质量特性层。在设计和制造过程中，往往需要把用户和相关方所关注的质量特性层层映射到产品的结构或零件之中，而这些结构或零件所具备的尺寸、公差、体积等质量特性称为微观质量特性。在机械产品中所对应是各组成件的质量特性。

1.2 机械产品质量特性分层集合

通过对不同类型的机械产品质量特性数据和专家意见收集、分析和整理，本文给出了机械产品质量特性分层集合如表1所示。

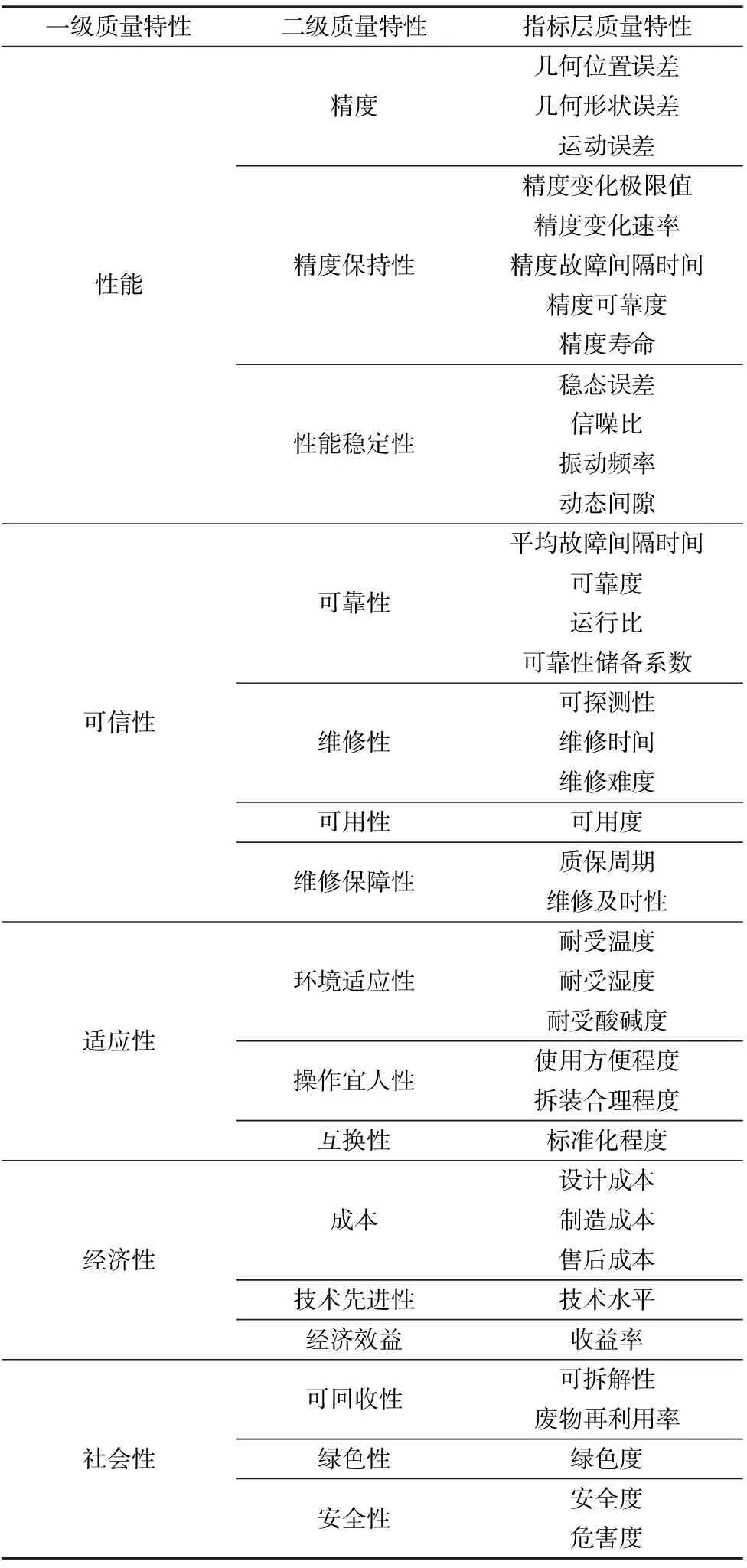
表1 机械产品质量特性分层集合

2 机械产品关键质量特性综合识别

结合EAHP、信息熵与模糊Borda综合方法的关键质量特性综合识别方法流程如图2所示。

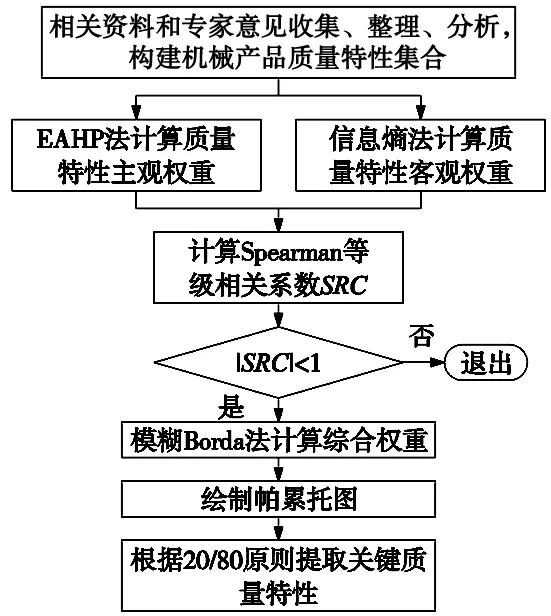
图2 机械产品关键质量特性识别方法流程

2.1 可拓层次分析法确定主观权重

可拓层次分析法分析步骤如下：

(1)构造可拓判断矩阵

可拓层次分析法的关键在于构造判断矩阵，可拓判断矩阵用C=(cij)n×n表示，如表2所示，

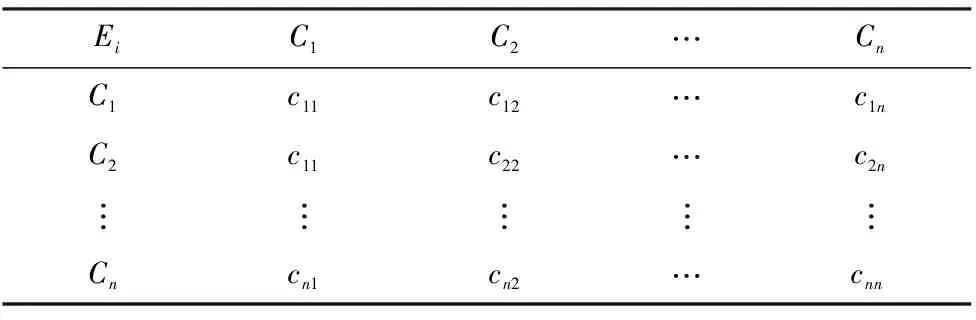
表2 可拓判断矩阵

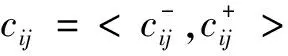
(2)求综合可拓判断矩阵、权重向量

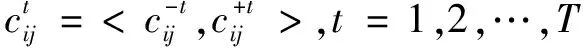
(1)

计算C-、C+的最大特征值对应的具有正分量的标准化特性向量x-，x+，根据公式(2)求p和q的值，判断是否满足一致性条件(0≤p≤1≤q)的权向量ρk=(ρk,ρk,…,ρk)=,k=1,2,…,n。

(2)

(3)层次单排序

(3)

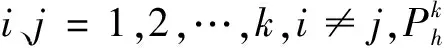
(4)层次总排序

(4)

式中，W2为单排序向量。

2.2 信息熵法确定客观权重

信息熵法分析步骤如下：

(1)构建决策矩阵

对于n个样本，每个样本有m个评价指标，则多指标的决策矩阵表示如下：

(5)

式中，i=1,2,...,m；j=1,2,...,n。

(2)规范化矩阵

对决策矩阵进行规范化处理，规范化矩阵如下：

(6)

(3)计算第j项指标熵值ej

计算第j个指标下，第i个方案的贡献度zij

(7)

计算第j项指标的熵ej

(8)

式中，k=1/lnnk=1/lnn，0≤ej≤1。当其中一指标与各方案的贡献度趋于一致时，ej→1，当完全相等时，此指标权重为0。

(4)计算指标权重值ϑj

(9)

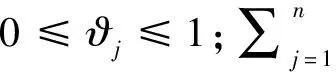
规范化处理可得到基于信息熵计算得到的权重向量

W2=(w1,w2,…,wn)

(10)

2.3 模糊Borda方法确定综合权重

斯皮尔曼等级相关系数(Spearman rank correlation,SRC)用于反映两组变量之间联系的密切程度，在组合方法中通常用SRC系数来衡量多种方法的相关程度[11]，设其中一种方法的等级排序为Ri，另外一种方法的等级排序为Si，SRC公式表示如下，用于表示两组排序结果的密切程度。

(11)

式中，i=1,2,…,n，-1≤SRC≤1。

综合EAHP、信息熵的模糊Borda综合排序步骤如下：

(1)极差变换公式计算隶属度μij

(12)

式中，xij为第i个质量特性第j种评价方法权重系数，μij为第i个质量特性第j种评价方法中属于优的隶属度。

(2)计算模糊频数qni

(13)

式中，当质量特性i排在第h位，δih=1，否则δh=0。

(3)计算模糊频率Nhj

(14)

(4)将排序转化为位次Qh

(15)

式中，Qh为质量特性i排在h位的得分。

(5)计算模糊Borda数FBi

FBi=∑hNhiQhi

(16)

2.4 关键质量特性识别

根据“关键的少数、次要的多数”质量管理理念，对综合排序结果绘制帕累托图。根据“20/80原则”，得到累积权重大于80%的所有质量特性，识别出机械产品的关键质量特性。

3 实例验证

元动作单元(meta-action unit,MAU)是仅考虑机械结构经过FMA分解得到的具有独立性结构单元，是典型的机械产品[12]。为此，本文选取某型号数控转台FMA分解树下的齿轮转动元动作单元作为分析对象[13]。

3.1 建立齿轮转动元动作单元质量特性分层集合

根据设计部门、工艺部门和用户使用数据收集、分析和整理得到如表3所示齿轮转动元动作单元质量特性分层集合。

表3 齿轮转动元动作单元质量特性分层集合

3.2 关键质量特性识别过程

(1)基于EAHP确定主观权重

根据EAHP分析流程，主观权重计算步骤如下。

步骤1：建立可拓判断矩阵

由项目组成员、企业技术人员、管理人员建立1个专家组，采用1～9标度法进行两两比较，根据公式(1)计算得到二级质量特性层B1～B6对目标层的可拓判断矩阵如表4所示。

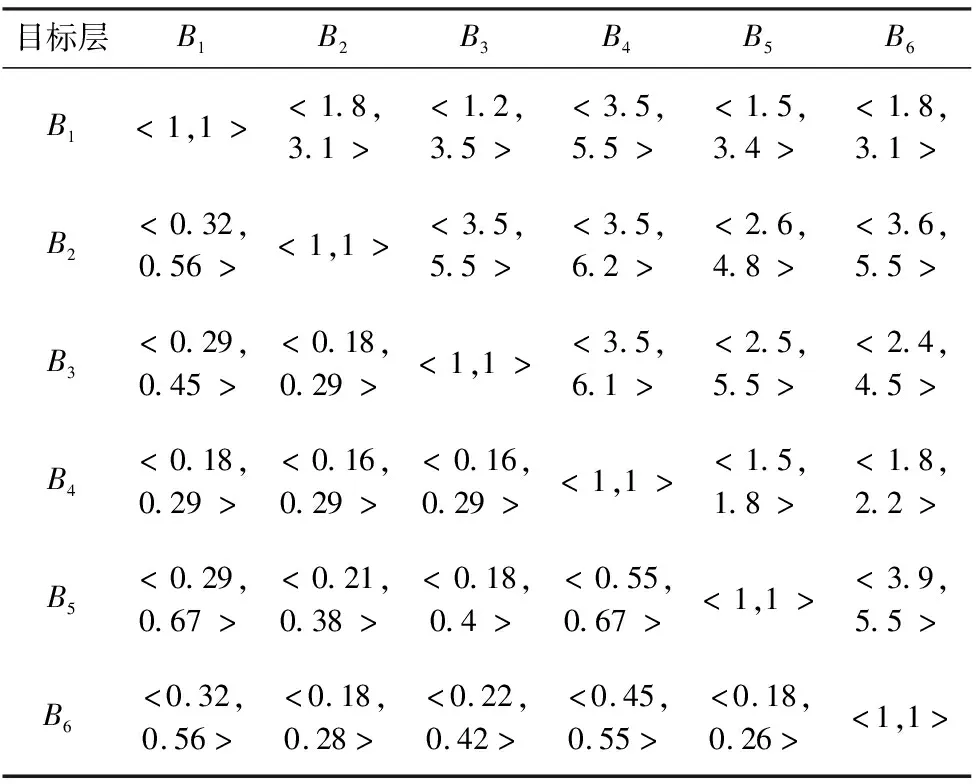
表4 二级质量特性层对目标层的可拓判断矩阵

步骤2：求权重向量

由表4可得：

计算得到：

x-=(0.62,0.661,0.251,0.162,0.124,0.118)T

x+=(0.643,0.618,0.37,0.137,0.193,0.106)T

根据公式(2)计算得p=0.87,q=1.03，满足一致性要求0

代入式(3)计算得到：

P1=(8.65,15.7,6.77,11.49,1.97,1)

归一化处理可得到二级质量特性权重向量，

W1=(0.19,0.344,0.149,0.252,0.043,0.022)

(2)基于信息熵确定客观权重

根据2.2节信息熵分析流程，客观权重计算过程如下:

如表3所示的质量特性分层集合，收集与数控转台齿轮转动元动作类似数据，对不能确定的质量特性指标按(好、较好、一般、差、很差)=(0.9,0.7,0.5,0.3,0.1)进行评分。得到如表5所示的质量特性指标数据表。

表5 齿轮转动元动作单元指标层质量特性数据

由式(5)～式(8)计算指标层各质量特性熵值向量为：

E=(0.997,0.991,0.990,0.995,0.997,0.990,

0.990,0.998,0.995,0.992,0.998,0.998,

0.988,0.955,0.944,0.998,0.998,0.995)

代入式(9)和规范化处理可得权重向量：

W2h=(0.026,0.090,0.101,0.049,0.031,0.097,0.094,

0.019,0.053,0.077,0.019,0.019,0.115,

0.045,0.060,0.019,0.019,0.019,0.047)

对指标层质量特性到对应的二级质量特性加权求和得到二级质量特性权重向量：

W2=(0.267,0.222,0.168,0.179,0.078,0.085)

(3)基于模糊Borda计算综合权重

对EAHP和信息熵两种方法计算的权重值，计算Spearman等级相关系数，

由SRC<1可见两种方法的排序结果关系密切。

根据式(12)～式(16)可得二级质量特性层所有质量特性的FB值。

FB=(2.514,3.56,0.477,1.764,0.026,0.046)

(4)绘制帕累托图

对综合分析所获得的权重绘制Pareto图如图3所示，根据“20/80原则”得到可靠性B2、精度B1、性能稳定性B4三个二级质量特性累计占比大于80%，因此可靠性、精度、性能稳定性为该数控转台齿轮转动元动作单元的关键质量特性。这一结果也符合用户和企业所关注的实际情况。

图3 数控转台齿轮转动元动作单元帕累托图

(5)对比分析

对本文所提方法所获得的权重结果进行对比分析如表6所示，EAHP方法所获得的权重没有考虑质量特性分析的客观性，信息熵法所获得的权重受数据影响大，本文所提方法充分结合了两种方法的优点，分析结果更加合理。

表6 各方法计算权重结果

4 结论

针对机械产品质量特性具有多样化和复杂性，关键质量特性识别主观性强、识别不准确问题。本文建立了结合可拓层次分析法(EAHP)和信息熵法的模糊Borda法综合识别方法，并通过实例验证了该方法的有效性和合理性。结果表明：①该综合识别方法能有效避免主观性的影响，并综合了客观权重，提高了识别结果的准确性。②该方法在没有大量数据的情况下，仍具有较好的识别效果，识别方法分析过程简单，具有一定的工程实际应用价值。