卧式加工中心空间精度预测及量化验证*

陈廷兵，李志强，敬正彪

(1.成都工业学院智能制造学院，成都 611730；2.成都工业职业技术学院装备制造学院，成都 610218)

0 引言

由机床各项几何误差元素耦合而成的空间精度是影响机床加工精度的关键因素，因此，精确构建机床完备空间精度模型以及准确溯源机床关键几何误差元素对提高机床加工精度具有重要意义。可为进一步探索空间精度补偿以及精度分配重要理论依据与工程技术支撑。

针对数控机床空间精度建模方面，主流模型搭建体系多以多体系统理论结合齐次坐标矩阵变换为理论基础。曲兴田等[1]利用均匀变换矩阵(HTMS)建立了九轴机床空间精度模型，借助梯度下降算法对某旋转磁台的位置坐标指令进行了实时修正补偿。YUEN等[2]针对三轴数控铣床提出了一种由反向传播神经网络确定的几何误差估计方法，并将其单独应用于几何误差补偿模型中。RAKSIRI等[3]同样以多体系统理论结合齐次坐标矩阵变换为理论基础，建立了机床通用空间精度模型。冯文龙等[4]以旋量理论与多体运动学理论为基础，从机床单个运动链到机床整体进行分析并建立了一种通用的误差模型，该模型可分离出影响可补偿与不可补偿位姿误差的几何误差源。在机床空间精度模型预测验证方面，提出了一种基于梯度下降算法的空间精度补偿方法。之后通过测量补偿前后机床进给轴的定位误差，验证了空间精度模型的正确性。黄华、GIVI等[5-6]通过引入误差相关性和误差补偿两个概念得到了一种优化的补偿方案，通过对比补偿前后工件加工精度，验证了所建空间精度模型。

综上所述，传统基于多体系统结合DH运动学构建机床空间精度模型已较为成熟，但主流建模方法因其需要建立多个局部坐标系存在奇异性的局限性，难以保证空间精度模型的完备性，同时已有研究大多沿用“补偿测量”或“补偿试切”的验证思想存在难以量化验证机床空间精度模型的局限性。因此，本文基于旋量理论建立了卧式加工中心空间精度预测模型且实现了模型的完备性，同时在借助“十二线法”分离几何误差的基础上输出了卧式加工中心空间精度预测模型，最终提出了一种新的模型量化验证方法，借助体对角线实验设计验证了该方法的正确性和有效性。

1 机器人运动学正解

已知任意刚体运动基本定义：刚体绕空间中某一个固定轴线进行旋转运动结合直线运动实现空间中某初始位置到结束位置的运动。基于旋量理论[5,7]以几何形式描述旋量运动过程如图1所示。其中，ω为旋转轴单位向量；q为截取空间轴线任意点；p取机器人末端位置(p0→pt)；t为时间段；d为移动距离。

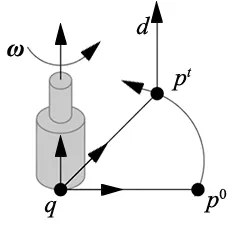
图1 旋量运动

基于基本旋量运动基础理论，推导某多自由度机器人运动学正解如图2所示，首先定义了某多自由度机器人两个重要坐标系，定义基座标系R在机器人底座中心位置，机器人末端执行器中心为末端坐标系E，假定在基座标系参考下的末端执行器位姿为E0，则γn为各关节单位旋量(微小变量)，φn为相对参考坐标系的各关节名义运动。因此某多自由度机器人运动学正解Eφ为：

图2 多自由度机器人

(1)

值得说明的是，基于旋量理论的机器人运动学正解在计算过程中全部以“矩阵左乘”为标准，而传统基于DH理论建模的推导过程全部以“矩阵右乘”为标准，因为基于旋量理论的旋量运动均以机器人基座标系为参考，而基于DH建模过程均以前一个关节坐标系为参考，因此矩阵相乘过程中存在差异，旋量理论建模的最大优势在于理论上仅设定一个基座标系为参考即可，规避了传统建模理论因多个局部坐标系建立存在的奇异性，规避了模型参数丢失的可能性。

2 卧式加工中心空间精度建模

2.1 几何误差分析

基于笛卡尔坐标系下的三轴卧式加工中心，主要以铣床为参考一般有X、Y、Z三个直线运动轴。以X轴为例描述几何元素，X轴进给时共计6项几何误差：δx(x)、δy(x)、δz(x)、εx(x)、εy(x)、εz(x)，同理Y轴、Z轴共计12项几何误差，共计18项与位置相关几何误差，与位置相关定义为几何误差随着机床进给存在变化[8]；与位置无关即为垂直度误差εxy、εyz、εzx，因此，三轴卧式加工中共计 21 项几何误差如表1所示；图3为21项几何误差原理图。

表1 21项几何误差

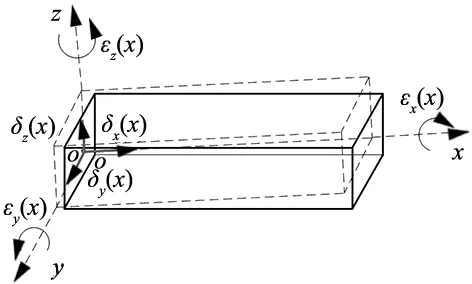
图3 几何误差原理图

2.2 运动链分析

为便于计算与理解机床空间精度基本原理，将机床运动链分为工件运动链与刀具运动链。工件运动链主要描述工件坐标系到床身参考坐标系，刀具运动链主要描述刀具坐标系到床身参考坐标系，一般地，理论初始位姿下工件坐标系与刀具坐标系原点重合，设机床基座标系(床身位置)为C_xyz，坐标原点为C0，一般认为机床开机启动回零后的位置为参考坐标系原点；工件坐标系设为W_xyz，一般将刀尖点设为刀具坐标系T_xyz，如图4所示。

图4 机床运动链简图

为实现机床空间精度建模的完备性，有必要确定刀具坐标系与工件坐标系相对于参考坐标系的初试位姿，三轴机床不存在姿态变化，因此得出刀具和工件坐标系在基坐标系下的位置坐标分别为：

(2)

(3)

式中，xT、yT、zT为刀尖点在机床坐标系下各轴的投影位置坐标；xW、yW、zW为工件切削点在机床坐标系下各轴的投影位置坐标。

理想状态下(几何误差未参与)，基于第1节旋量理论结合式(2)和式(3)，不难得出刀具运动链与工件运动链末端理想运动矩阵为：

(4)

(5)

式中，ECT为刀具相对基坐标系的运动矩阵；ECW为工件相对基坐标系的运动矩阵。

实际状态下(几何误差参与)，机床进给过程中存在几何误差，将几何误差以旋量形式带入式(4)和式(5)中，不难得出实际刀具链与工件链运动矩阵为：

(6)

(7)

式中，ECT为刀尖相对机床坐标系的实际运动矩阵；ECW为工件切削点相对机床坐标系的实际运动矩阵。

2.3 空间精度预测建模

机床空间精度的基本定义为：机床实际进给过程中因为几何误差的存在，导致了机床刀尖点偏离了工件切削点的过程视为机床空间精度。结合2.1节、2.2节中分析，推导出了该卧式加工中心空间精度模型ΔE为：

ΔE=ECW-ECT=[ΔxΔyΔz0]T=

(8)

式中，x、y、z为各轴设定进给行程；Δx、Δy、Δz为各轴空间精度分量。

综上所述，该卧式加工中心空间精度建模过程首先推导了基于旋量理论的机器人末端运动学正解过程，然后将旋量理论推广到机床领域，通过分析三轴卧式加工中心21项几何误差，机器人结合机床两条运动链建立了运动链理论与实际运动学矩阵，两条运动链运动矩阵建立过程即为机器人运动学正解推导过程，进而基于机床空间精度基本定义构建了该卧式加工中心空间精度模型，不难看出，空间精度模型包含了21项几何误差，保证了模型的完备性，规避了传统建模方法因奇异性导致的几何误差丢失的可能性，同时减少了局部坐标系的建立；此时，模型仅为函数参数模型，为实现机床空间精度预测模型，因此有必要开展几何误差辨识研究。

3 几何误差辨识

3.1 空间理想位置与实际位置模型

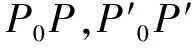
图5 理想与实际位置

(9)

因误差存在的原因，实际点P0′(x0，y0，z0)至P′(x，y，z)的距离为：

(10)

则理想距离与实际距离之差为：

ΔL=L′-L

(11)

ΔLi=[Δxi-Δx0,Δyi-Δy0,Δzi-Δz0,1]=

[ΔLxcosα,ΔLycosβ,ΔLzcosγ,1]T

(12)

式中，ΔLi为空间中任意一条有限线段的实际测量误差值。

3.2 定位误差元素辨识

通过测量机床轴线方向偏差，得到各轴定位误差δrri为：

δrri=ΔLi(ri),r=x,y,z

i=1,2,…,n

(13)

式中，ΔLi(ri)为各轴测量线上任意测量点。

3.3 俯仰与偏摆误差元素辨识

通过测量轴线方向以及空间中与此轴线平行的偏差从而辨识直线度误差元素εsti为：

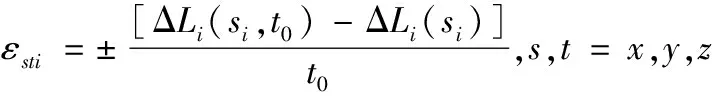
i=1,2,…,n

(14)

式中，ΔLi(si，t0)和ΔLi(si)均为空间中与某轴线平行测量线上的任意测量点，当s=y，t=x；s=z，t=y；s=x，t=z时，等式取正，其余取负。

3.4 直线度误差元素辨识

直线度误差元素辨识借助已辨识俯仰与偏摆误差元素计算得出：

i=1,2,…,n

(15)

式中，δuw为w轴u方向上的直线度误差元素，εvw为偏摆或俯仰误差元素，Pvw为εvw积分结果，并且εvw以n阶多项式形式输出为：

εvwi=a0+a1x+…+anxn

(16)

Nvwi为Pvwi一阶拟合曲线，不难得出：

Pvwi=c0+c1vi

(17)

基于最小二乘法求解常数项c0、c1即可。

3.5 分离滚角与垂直度误差元素

滚角误差元素为εrri，同样以n阶多项式形式给出：

(18)

式中，assi为常数项。

将已辨识误差元素以及未知的滚角和垂直度误差元素带入ΔLi中，通过测量三条面对角线(i+1)个点的偏差，带入ΔLi中解耦出三个相互独立的(i+1)阶方程组，求解方程组分离滚角误差元素εrri与垂直度误差元素Suv，(uv=x,y,z)。

此处值得说明的是，某些机床进给方向并不符合笛卡尔坐标系X、Y、Z方向，因此基于“十二线法”实验设计过程中，应该保证机床实际切削进给方向与笛卡尔坐标系保持一致，规避实际进给方向与G代码运动轨迹相反导致实验失败的可能性。

4 空间精度量化验证

4.1 空间精度预测

机床空间精度预测模型为后续空间精度补偿提供了一定的可能性，但少有研究学者提供其空间精度预测云图，本位为直观表示机床空间精度预测趋势，基于第3节中“十二线法”几何误差辨识理论，设定该卧式加工中心加工空间范围为600×600×600 mm，输出了机床加工空间精度预测云图如图6所示。

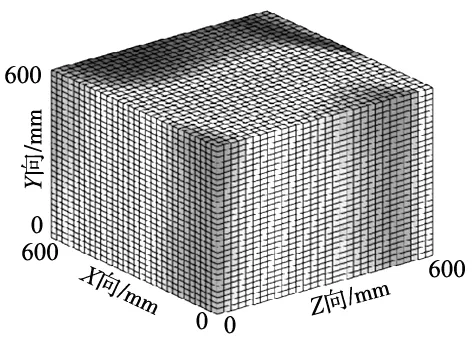
图6 加工空间空间精度预测云图

云图中接近红色区域代表该区域空间精度较差，靠近深蓝色区域代表该区域空间精度较好，加工空间精度预测云图直观描述了机床工作区域内部的精度变化，同时可以看出，该卧式加工中心正极限位置加工精度较优，反之则较差；该预测云图同样实现了机床工作空间内任意点空间精度预测，即提供任意位置获取该点空间精度预测结果，为后续空间精度补偿奠定了良好的理论与数据基础。

此处空间精度预测结果仅基于“十二线法”辨识结果给出，并未进行实验验证，因此有必要开展体对角线实验设计工作保证该预测结果的准确性。

4.2 实验验证

完备空间精度模型是实现空间精度补偿的基础，但前提条件必须证明模型准确、合理。因此，在基于ISO230-6:2002[6]的基础上提出一种新的空间精度预测模型验证策略，开展体对角线实验，验证空间精度模型的准确性。

如图7所示，借助雷尼绍激光干涉仪为测试仪器，搭建如PPN空间体对角线定位精度测试平台，开展4条空间体对角线定位精度测试实验，测量时，各对角线均布选取21个采样点，其中，D0为实验测量起始点，即工件坐标系原点C0。

图7 空间体对角线测量实验平台

现以对角线PPP举例说明，如图8所示。设iDi、iDi+1为PPP上理想(ideal)任意相邻两点，ΔiDi,i+1(虚线)为其空间矢量；因空间精度作用，测试PPP对角线定位误差时，实际(reality)两点间的空间矢量为ΔrDi,i+1(实线)；同样，所建立完备空间精度模型可预测(predictin)两点间的空间矢量为ΔpDi,i+1(点划线)。因此，以ΔiDi,i+1为理论参考基准，对比ΔrDi,i+1、ΔpDi,i+1与ΔiDi,i+1之间的偏差，根据实际需求，保证相对误差在合理范围内，即可验证所建空间精度模型的完备性。

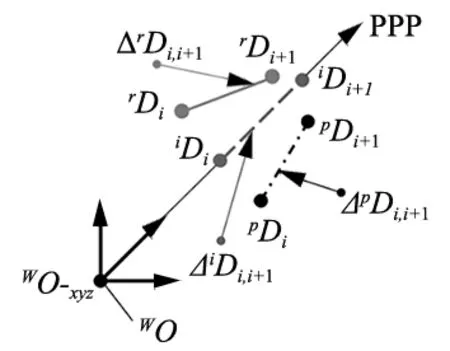
图8 验证策略

该验证策略具体实施步骤如下：

①计算理想矢量ΔiDi,i+1。理想状态下，未有空间精度参与，输入任意相邻采样点iDi、iDi+1名义坐标，即可得出ΔiDi,i+1；

②计算预测矢量ΔpDi,i+1。将空间精度作用下的两点rDi、rDi+1坐标带入空间精度模型式(8)中，即可预测ΔpDi,i+1；

③计算实际矢量ΔrDi,i+1。借助图7中体对角线定位误差测试实验，获取实测采样点rDi、rDi+1，计算实测矢量ΔrDi,i+1；

④计算偏差。为保证计算结果以微米数量级输出，ΔrDi,i+1、ΔpDi,i+1均减去公共部分理想矢量ΔiDi,i+1得出相对偏差，如图9所示。

图9 空间矢量对比

结果显示，由于所得数据为微米级别，预测数据与实验数据相差甚微，极限偏差仅为3.9 μm，PPP、NPP、PNP、PPN平均偏差分别为-0.21 μm、-1.06 μm、-1.68 μm、-0.05 μm，由此可以看出，实际上模型预测数据与实验实测数据符合程度较高，因此，验证了所建基于旋量理论的空间精度完备预测模型准确、合理，可为后续机床空间精度补偿奠定基础，具有实际工程意义。

5 结论

基于旋量理论推导多自由度机器人运动学正解，将其推广到机床领域后，通过分析机床21项几何误差和机床运动链分析，同时基于机床空间精度定义，实现了该卧式加工中心空间精度模型的搭建。

借助“十二线法”完成了几何误差辨识理论推导过程，为该卧式加工中心空间精度预测提供理论基础，同时输出了该机床空间精度预测云图。基于ISO230-6:2002体对角线空间精度评定标准，对比了对角线模型预测值与实验测量值。结果显示四条体对角线符合程度较高，验证了所建基于旋量理论的空间精度完备预测模型准确、合理，可为后续机床空间精度补偿奠定基础，具有实际工程意义。