改进的差分进化算法在约束优化问题中的应用*
2022-01-27袁庆霓孙睿彤衣君辉施辉城
白 欢,袁庆霓,王 鑫,孙睿彤,衣君辉,施辉城
(贵州大学现代制造技术教育部重点实验室,贵阳 550025)
0 引言
约束优化类问题在现实生活中无处不在,然而求解该类问题的算法却很少。与无约束类问题不同,约束类问题求解的关键是最优解必须满足所有的约束条件,约束条件的限制不仅使得可行区域变小、搜索空间变得复杂,而且约束条件也难以处理,大大地增加了求解的难度。因此,目前对约束类问题的研究,绝大多数研究者采用的是约束处理技术。李智勇等[1]详细地综述了约束优化问题的求解方法和常用的约束处理技术。
在进化算法中,差分进化(DE)算法具有结构简单、参数少、收敛性好和搜索能力强的特点[2-3],因此,很多研究者将DE算法与约束处理技术结合来求解约束优化问题。刘若辰等[4]提出一种改进的自适应约束差分进化算法,但是该算法对个体的评价侧重于个体是否违反约束条件,在后期搜寻最优解时精度不高,这是因为种群中保持适当的不可行个体数量有助于提高收敛性[1],同时也是找到全局最优解的关键。TOSCANO等[5]提出在变异过程中父代向量采用随机排序法,提高了种群多样性,但是收敛速度较慢。WANG等[6]将广义反向学习策略用于生产初始种群,有效地利用了反向解的信息,然而在后代的进化过程中没有使用该策略,未能有效利用其优势。吴文海等[7]对文献[6]的不足作了改进,但是对于进化过程中缩放因子的选取未能体现出对多样性和最优解的保护。受文献[4-7]的启发,本文提出一种改进的差分进化算法(GOBL-RDE)来求解约束优化问题。利用广义反向学习算法生成反向种群并在后期进化过程中约束种群的搜索空间,加快算法收敛速度;对于变异操作为固定值的缺点,根据可行率自适应采用两种变异策略,并设计了自适应交叉因子和缩放因子,有效地利用了“优秀”个体资源,提高了种群的多样性;在选择操作中,将常用的“贪婪”选择作了改变,通过将变异前的种群与变异后的种群混合,经排序后选择不同的Np个个体作为新种群。通过与其他几种约束进化算法进行比较,实验证明在处理约束类问题时,GOBL-RDE算法在最优解上收敛精度更高,收敛速度更快。
1 相关知识
1.1 约束优化问题
约束优化问题中,约束条件有等式、不等式及边界约束等形式,可按照以下方式做出定义:
minimize:f(x),x∈D
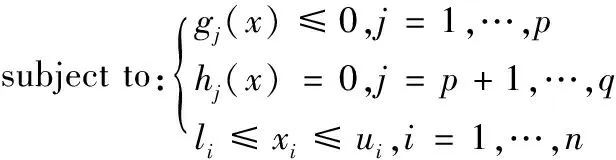
(1)
其中,x=(x1,x2,…,xn)∈D⊆Rn为n维决策空间;f:D→R为目标函数;gj(x)≤0表示不等式约束;hj(x)=0表示等式约束;p、q分别表示不等式和等式约束的个数;ui和li分别为xi的上、下界。处理等式约束时,通常将其转化为相应的不等式约束:
|hj(x)|-δ≤0,j∈{p+1,…,q}
(2)
式中,δ为正容忍因子,本文取值为0.000 1。
解x到第j个约束的距离定义为:
(3)
则解x到可行域的距离定义为约束违反程度G(x),可表示为:
(4)
1.2 广义反向学习算法
广义反向学习[8]概念定义如下:

(5)
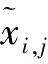
xi,j=rand(aj,bj)
(6)
广义反向学习算法能有效地利用反向解的资源,扩大搜索方向,提高搜索效率。在进化过程中约束了种群的搜索空间,加快了算法收敛速度和效率。
初始化阶段伪代码如下:

算法1 初始化阶段的广义反向学习(GOBL)策略(1)随机产生初始化种群P0;#种群数量为Np;(2)for i=1:Np(3) for j=1:n(4) P1i,j=k×(aj+bj)-P0i,j(5) ifP1i,j
在P0和新种群P1中择优选取Np个个体。
进化时伪代码如下:

算法2 进化阶段的广义反向学习(GOBL)策略(1)ifrand(0,1)
在Pt和新种群P1中择优选取Np个个体。
1.3 自适应权衡模型机制
在处理约束类问题时难免会出现不满足条件的个体,为了更好的处理约束条件对适应值的影响,自适应权衡模型(ATM)机制[9]是将种群划分为:不可行、半可行和可行状态,并分别计算其适应值。
在不可行状态下,个体均不满足约束条件,使用个体的违约值代替适应值。
ffitness(xi)=G(xi)
(7)
在半可行状态下,有一部分个体满足约束条件,使用适应值转换(AFT)策略[10]来执行转换。
AFT策略是根据个体是否满足约束条件分为集合Z1和Z2,其中Z1、Z2分别表示满足和不满足约束条件的个体序号。
Z1={i|G(xi)=0,i=1,…,N}
Z2={i|G(xi)>0,i=1,…,N}
(8)
个体xi的目标函数值f(xi)根据下式进行转换:
(9)
式中,φ为可行率,f(xbest)、f(xworst)分别为Z1中最好和最差的个体序号。
接着,将目标函数值f(xi)标准化
(10)
将违约值G(xi)标准化
(11)
则个体最终适应值为
ffinal(xi)=fnor(xi)+Gnor(xi),i∈(1,…,N)
(12)
在可行状态下,个体均满足约束条件。使用个体目标函数值代表其适应值。
ffitness(xi)=f(xi)
(13)
2 改进差分进化算法
2.1 改进的个体选择机制
利用GOBL策略获得原种群及反向新种群,此时需筛选出较优的Np个个体,而传统的DE算法在选择操作时是将种群中父代向量的每个个体与新种群中对应的个体逐个进行适应值比较,保存适应值较优的个体,在这种筛选机制下可能会出现两个适应值都较优秀的个体进行比较,但是也会出现两个适应值都较差的个体进行比较,那么此时必然会有一个适应值较差的个体被保留,这无疑会影响进化速度,而且容易陷入局部最优[11],因此本文设计一种改进的选择机制来加快进化速度。具体操作如下:首先将父代种群与新种群合并,然后计算其适应值并作排序处理,最后选择较优的Np个不同的个体。
个体选择机制伪代码如下:

算法3 个体选择机制(1)执行ATM机制计算个体适应值;(2)根据适应值对个体进行排序;(3)选取靠前的Np个个体。
2.2 差分变异
2.2.1 个体排序及概率计算
在差分变异过程中,为了利用种群中“优秀”个体的资源,对个体适应值由优到差进行排序[12],个体xi的排序值由下式表示:
Ri=N-i,i=1,2,…,N
(14)
式中,N表示种群中个体的数量(本文N=50),i为第i个个体在种群中的排序值。
个体排序后需要将个体被选择的概率计算出来。约束优化问题中,为了更好地体现个体间的支配关系,根据可行率分别选择模型计算,本文采用以下公式进行概率Pi计算[13]:
(15)
式中,i=1,2,…,N,λ=0.5或2。λ值的选取直接影响了参与变异的个体,从而影响最优解的搜索范围。
如图1所示,R1、R2为种群中排序后的两个个体,其两个个体在模型一(λ=2)下的选择概率分别为p1、p2,在模型二(λ=0.5)下的选择概率分别为p3、p4,由图1知,p2-p1>p4-p3,且两者差值较大,这表明模型一下个体间的支配关系比模型二更加显著。进化初期,满足约束条件的个体较少,该阶段的主要目的是使不可行个体满足约束条件,增加可行个体的数量,因此采用模型一能充分利用“优秀”个体资源加快搜索速度。当种群处于可行状态下时,若仍然用模型一,那么一些表现稍差的个体被选中的概率大大降低,同时被选中参与变异的个体的数量也会减少,容易陷入局部最优,降低种群多样性,故采用模型二效果更好。
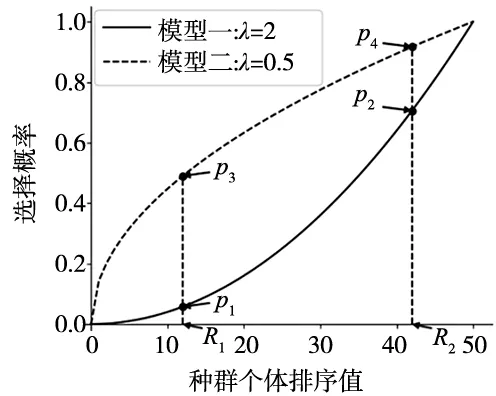
图1 不同模型下的概率计算
2.2.2 自适应变异策略
DE/rand/2策略在进化后期搜索中效率低,收敛速度慢,而DE/best/2策略收敛性好,但是难以维持种群的多样性[14]。为了同时具备以上两者优点,本文采用自适应变异策略,方法如下:
(16)
式中,xi,t、xr1,t、xr2,t、xr3,t、xr4,t为第t代中不同的个体;vi,t为变异后产生的试验向量;xgbest为进化过程中适应值最优个体;F为缩放因子,F∈(0,2);rand为随机数,rand∈(0,1);φ为可行率。进化初期,可行个体数量少,因此φ值较小,DE/best/2被选择的概率较大,即利用最“优秀”的个体资源引领其他参与变异的个体向该个体进行学习,加快了收敛速度。进化后期,可行个体数量多,因此φ值较大,DE/rand/2被选择的概率大,保证了种群的多样性。若变异生成的个体超出边界范围,则在其允许范围内再次随机初始化。
2.2.3 改进的自适应缩放因子及交叉因子设计
在DE算法中,参数缩放因子F和交叉因子Cr对算法的寻优能力有直接的影响,为了避免算法中参数固定,本文使用自适应缩放因子F和自适应交叉因子Cr。具体计算如下:
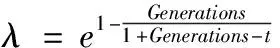
F=F0×2λ
Cr=0.5×(1+rand)
(17)
式中,Generations表示迭代次数的最大值;t表示当前迭代次数;F0为常数,F0∈(0,1);rand为随机数,rand∈(0,1)。通过测试发现,当常数F0取值较小时,算法的收敛速度较慢,最优解搜索能力较差;当常数F0取值较大时,尽管收敛速度得到了改善,但是最优解搜索能力仍然较差;通过实验发现当常数F0=0.5时算法的整体性能最佳。
在进化初期,大部分个体有较差的适应值,由式(17)知,F具有较大数值,扩大了搜索空间,减少了对个体信息的利用,保持了种群的多样性。随着迭代次数逐渐增加,F取值逐渐减小,直到后期收敛于常数F0,这有利于保持种群中的“优秀”个体资源,防止其遭受破坏并增大了寻到最优解的几率。交叉因子Cr采用随机函数生成,其平均值为0.75。具体算法如下:
变异伪代码如下:

算法4 变异伪代码(1)根据适应值对个体Ri进行排序;(2)按照种群所处状态选择相对应的概率计算模型;(3)计算种群中每个个体的被选择的概率Pi;(4)根据选择概率选择4个不同的个体;(5)按式(17)计算缩放因子F和交叉因子Cr;(6)按式(16)生成vi,t。
3 算法步骤
结合上述内容,本文GOBL-RDE算法步骤如下:
本文算法步骤如下:

算法5 本文算法(GOBL-RDE)步骤(1)设置相关参数;(2)执行算法1和算法2生成初始种群;(3)执行算法3选择个体;(4)执行算法4生成vi,j;(5)执行算法3选择个体;(6)执行算法2;(7)判断是否达到精度要求或最大迭代次数,若是,则结束;否则跳转到步骤(4)。
4 算法测试与分析
为测试算法性能,采用经典的约束测试函数[15]中的13个函数进行验证。分析GOBL算法的有效性,并与εRDE[16]、GOBL-ACDE[7]和ATMES[10]三种算法在最优值、平均值、最差值以及标准差等指标进行比较。
4.1 参数设置
广义反向学习算法中,k值能影响反向个体资源,Jr表示进化时执行广义反向学习算法的概率,在整个GOBL-RDE算法框架中k和Jr值的选取会影响算法的性能,为了使得算法简单,本文将其设为固定值,本文算法中k取0.2,Jr取0.8,最大迭代次数为2000,其余参数采用自适应设计。
4.2 若干改进策略对于算法性能影响分析
为了验证个体排序对算法收敛速度的影响,利用测试函数g01和g08分别执行GOBL-RDE和GOBL-DE(个体不作排序处理)算法验证个体排序的有效性,比较结果如图2所示,其中实线表示GOBL-DE算法,虚线表示GOBL-RDE算法。由图2知虚线收敛速度更快,因此可以认为利用优秀个体资源可加快算法收敛。

(a)g01收敛图 (b)g08收敛图
为了验证GOBL对算法收敛速度的影响,分别将测试函数g03、g06、g09利用GOBL-RDE与RDE(进化阶段不使用GOBL算法)算法进行比较,迭代次数为2000次,三个函数的收敛结果如图3所示,其中实线表示RDE算法,虚线表示GOBL-RDE算法。由图3可知,g03和g06两种算法最终结果收敛到同一值,但是虚线的速度更快,而g09两种算法收敛值接近,但是虚线的收敛速度和精度更高,因此可以认为GOBL算法加快了收敛速度。
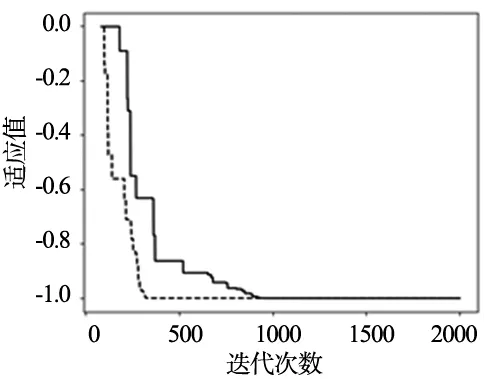
(a)g03收敛图
为了验证算法的收敛精度,将GOBL-RDE算法与GOBL-ACDE、εRDE和ATMES几种约束优化算法进行比较,算法比较结果如表1所示,表中加粗的表示较优的值。
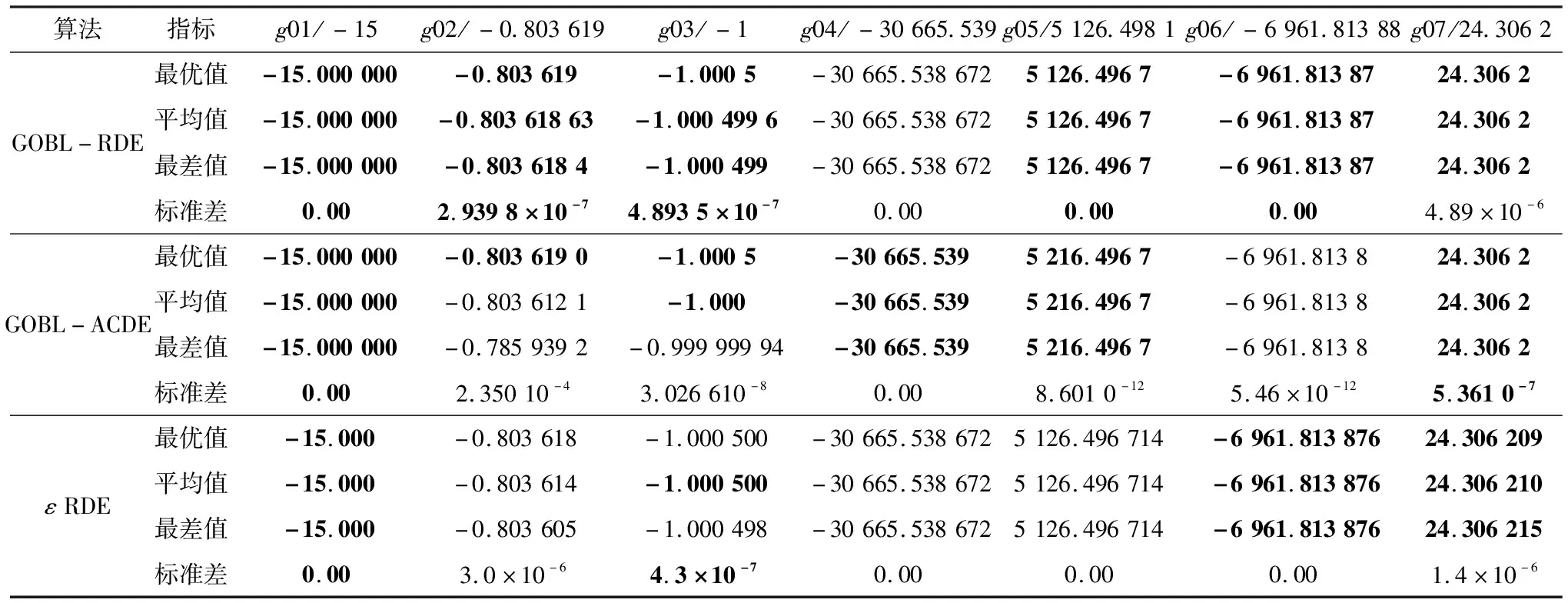
表1 GOBL-RDE与GOBL-ACDE、εRDE和ATMES算法比较
由表1可以看出,在函数g02、g03、g05、g08、g11测试中,GOBL-RDE算法的前三项指标均优于其它算法,而其中就有三个函数(g03、g05和g11)均包括等式约束,这说明GOBL-RDE算法在处理含有等式约束时效果比较好。对于像g02这种可行区域非常大的函数,进化时种群直接进入可行状态,因此可以忽略上述4种算法在约束处理机制上的差别,只需要考虑算法在最优值处寻优的搜索能力,从表1知,只有GOBL-RDE和GOBL-ACDE两种算法寻到最优值,其余算法均未寻到,但是在其他三项指标方面,GOBL-ACDE算法结果略差于GOBL-RDE算法,因此可以认为GOBL-RDE算法的寻优能力较好。在约束条件比较多(5个及以上)的情况下,这类函数对约束条件的处理是找到最优解的关键,本文中有函数g01、g04、g05、g07和g10,虽然GOBL-RDE在函数g04的三项指标稍差于GOBL-ACDE,但是在g05、g07、g10上,GOBL-RDE算法每个寻优指标均优于其余算法,因此可以认为GOBL-RDE算法在约束处理机制方面是较优的。与εRDE相比,GOBL-RDE只在g03和g06两项结果表现稍差,这说明GOBL-RDE比εRDE有更好的寻优精度。与GOBL-ACDE相比,虽然GOBL-RDE和GOBL-ACDE基本在13个测试函数均可达到全局最优,但是GOBL-ACDE在函数g02、g03、g06、g08、g11上各项指标表现稍差。与ATMES相比,GOBL-RDE除了在函数g04、g06上表现稍差,在其它函数上三种指标均优于ATMES算法。GOBL-RDE在13个测试函数中标准差较小,这说明稳定性表现较好,因此可以认为GOBL-RDE寻优性能更好。
5 结论
本文提出一种改进的差分进化算法用于求解约束优化问题,算法利用GOBL算法产生反向种群提高了搜索效率。改进了变异策略单一的缺点,并通过参数自适应方式选择变异策略,改进了缩放因子,有效地利用了“优秀”个体资源,降低了陷入局部最优的几率,保持了种群的多样性;在选择操作中,对传统的“贪婪”机制作了改进,并充分利用反向解资源,加快了收敛速度。通过与几种约束算法进行比较,结果证明在处理约束类问题时,本文提出的算法有较高的收敛精度,而且收敛速度较快。
