ITO连接过孔电阻定量计算与设计方法
2022-01-27高玉杰
周 焱,王 超,陈 鹏,朱 宁,江 鹏,高玉杰
(武汉京东方光电科技有限公司,湖北 武汉 430040)
1 引 言
薄膜晶体管液晶显示器(TFT-LCD)已成为目前平板显示的主流产品,相关设计和制造工艺已进入成熟阶段[1]。薄膜晶体管的配线材料均采用导电性极好的金属材料,如铝、铜。相对于铝,铜具有更低的电阻率、更快的刻蚀速度,目前被广泛使用在中大尺寸TFT-LCD面板中[2-6]。TFT-LCD面板中不同金属层之间的导通均需通过过孔连接,而连接过孔的材料使用较多的就是氧化铟锡(ITO)。ITO是一种金属氧化物,具有良好的导电性和高的光学透过率,作为透明电极被广泛应用在TFT-LCD中,成为不可或缺的一部分[7-8]。由于ITO的电阻率比金属材料大2~3个数量级,同时ITO与金属两种不同属性材料的接触界面同样存在着较大的接触电阻,故ITO连接过孔是电信号在传递过程中电阻相对较大的区域,流经电流过大时容易发生过孔烧毁的问题。因此在产品设计中,如何合理设计过孔电阻是提高产品品质的重要课题[9]。
白金超等人研究了铝配线情况下的过孔接触电阻的变化规律,指出了过孔面积、尺寸等因素与接触电阻大小的定性关系,为传统铝工艺下的过孔设计提供了依据[10]。业内还没有一种可定量计算和设计过孔的方法。而且,目前业内已广泛使用铜配线,辅助层结构与铝配线有所不同,刻蚀特点也有很大差异,铜工艺下的过孔接触电阻规律还需要进一步研究。
本文通过对过孔电阻的阻值进行分解,得到并验证了定量计算过孔电阻的方法,阐明了铜工艺下的过孔接触电阻变化规律,同时为复杂的过孔设计提供了一些参考,最后探索了过孔电阻与击穿电流的关系,为合理设计过孔提供了依据。
2 实 验
实验材料为大尺寸TFT半成品玻璃基板若干。玻璃基板上的成膜顺序依次为栅极金属层(Gate)、栅极绝缘层(GI)、源漏极金属层(Source/Drain,SD)、薄膜晶体管钝化层(PVX)、像素电极层。物理溅射形成钼铌/铜/钼钛(MoNb/Cu/MTD)15 nm/600 nm/20 nm的Gate层和钼铌/铜(MoNb/Cu)15 nm/500 nm的SD层金属,以及50 nm ITO的像素电极。等离子增强化学气相沉积氮化硅形成420 nm的GI层和400 nm的PVX层。通过一次干法刻蚀,在PVX层上形成过孔使ITO与SD层金属相连(浅孔),在GI层和PVX层上同时形成过孔使ITO与Gate层金属相连(深孔)。
本文采用Kesight B1500A半导体参数分析仪对样品上具有开尔文四线检测结构的过孔接触电阻进行测试,采用Keithley 2410 1 100 V高压源测量设备对普通过孔电阻和击穿电流进行测试,通过扫描电子显微镜(SEM)、能量色散X射线光谱仪(EDS)和聚焦离子束显微镜(FIB)对过孔内部形貌进行表征。数据的相关性分析采用JMP软件16版进行。文中描述的孔尺寸均为刻蚀后的孔底部尺寸(Final inspection critical dimension,FICD)。
2.1 过孔电阻的阻值分解
图1为TFT-LCD常见的ITO连接过孔的截面图。图中①为孔间的ITO平面电阻,②为孔间的ITO斜坡电阻,定义Rito为孔间连接的ITO总电阻,包括①和②两部分。③为ITO与金属的接触电阻,其中Rd为深孔接触电阻,Rs为浅孔接触电阻。很明显,电流要从Gate层流到SD层,必须经过①、②、③,因此单过孔电阻的阻值:

图1 ITO连接过孔截面示意图
Rvia=Rd+Rs+Rito.
(1)
图2为ITO连接过孔的平面俯视图。Rito等于平面电阻与斜坡电阻之和。假设ITO的方块电阻为R□,深浅孔间的ITO总长度为LR,深浅孔间的ITO宽度为W,则
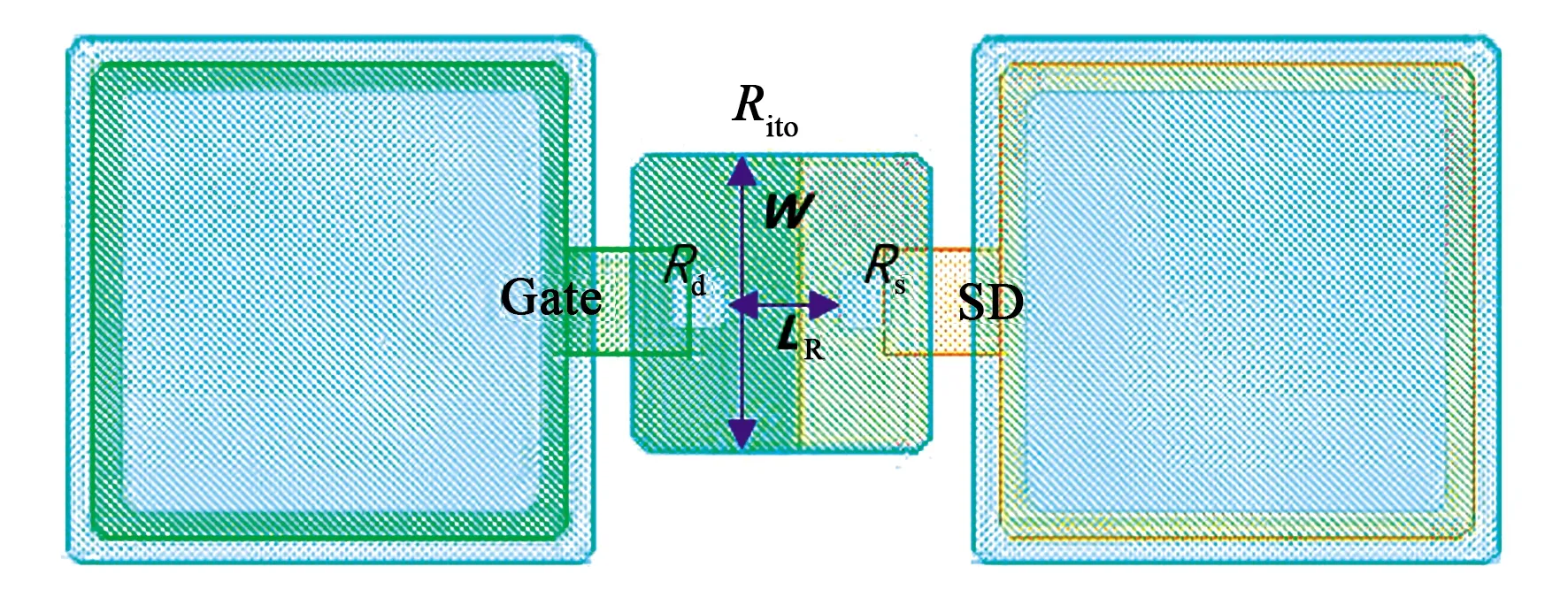
图2 ITO连接过孔平面俯视图
Rito=R□·LR/W.
(2)
假设孔边缘的坡度角为α,深浅孔之间的距离为LF,则深浅孔之间的ITO总长度:
(3)
其中:TGI和TPVX分别为GI层和PVX层的厚度。Rd和Rs为接触电阻,与过孔尺寸相关,没有可用的理论计算公式。我们采用开尔文四线检测法测量设计好的过孔拟合得到接触电阻与过孔尺寸的计算公式。图3为具有开尔文四线检测结构的过孔接触电阻图形。

图3 具有开尔文四线检测结构的过孔接触电阻图形。(a)深孔;(b)浅孔。
2.2 复杂结构过孔的阻值分解
在实际的面板设计中,常见到的是多行多列的复杂过孔结构设计。下面分别对3种常见的过孔结构进行阻值分解和说明。
2.2.1 单排孔设计
如图4所示,单排孔设计是深孔和浅孔各只有一列面对面排列的情况,深孔m个,浅孔n个,m和n可以相等也可以不相等。通常多个深孔都是相同设计,多个浅孔也是相同设计,相同设计的孔接触电阻可以认为无差异。
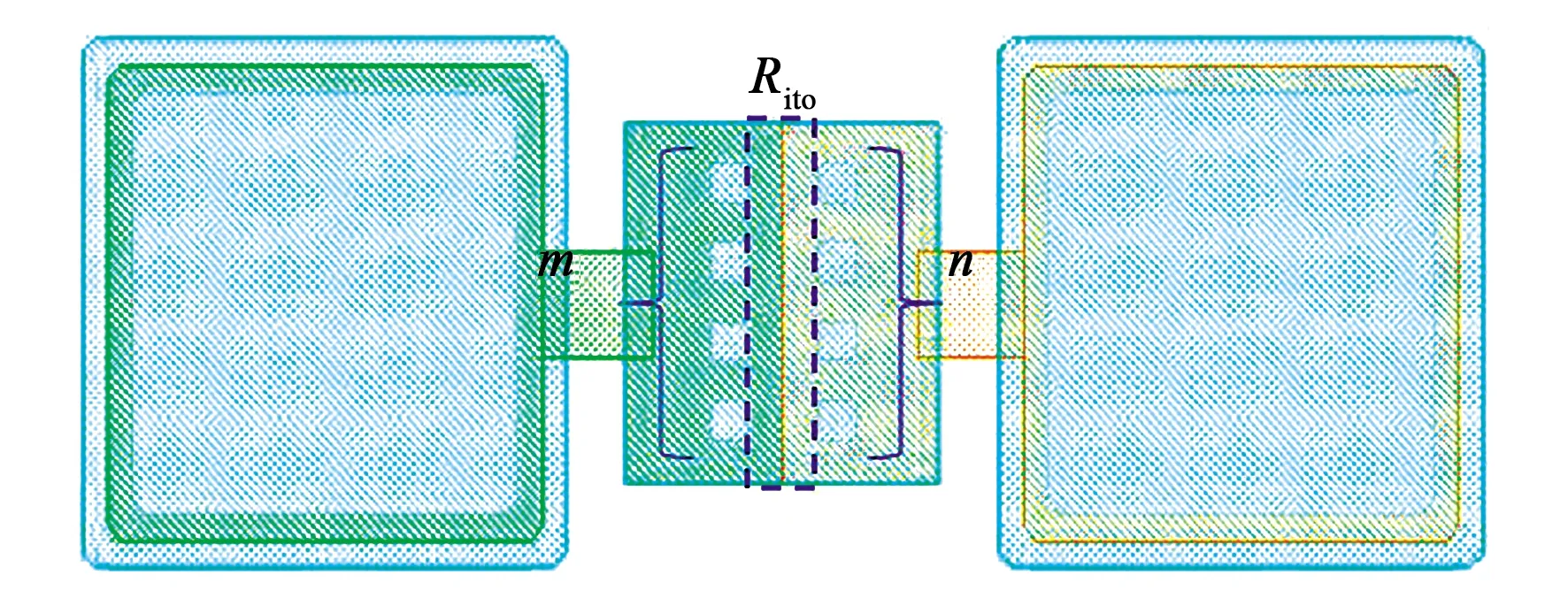
图4 单排孔结构的ITO连接过孔电阻图形
电流依次流经深孔、ITO和浅孔。深孔接触电阻、ITO连接电阻和浅孔接触电阻之间是串联关系,m个深孔之间则是并联关系,n个浅孔之间也是并联关系。单排孔结构的过孔电阻等效电路图如图5所示。

图5 单排孔结构的过孔电阻等效电路图
于是,我们很容易得到单排孔结构的过孔电阻为:
(4)
2.2.2 双排孔竖向设计


图6 双排孔竖向结构的ITO连接过孔电阻图形
电流依次流经深孔、ITO和浅孔,双排孔竖向结构的过孔电阻等效电路图如图7所示。
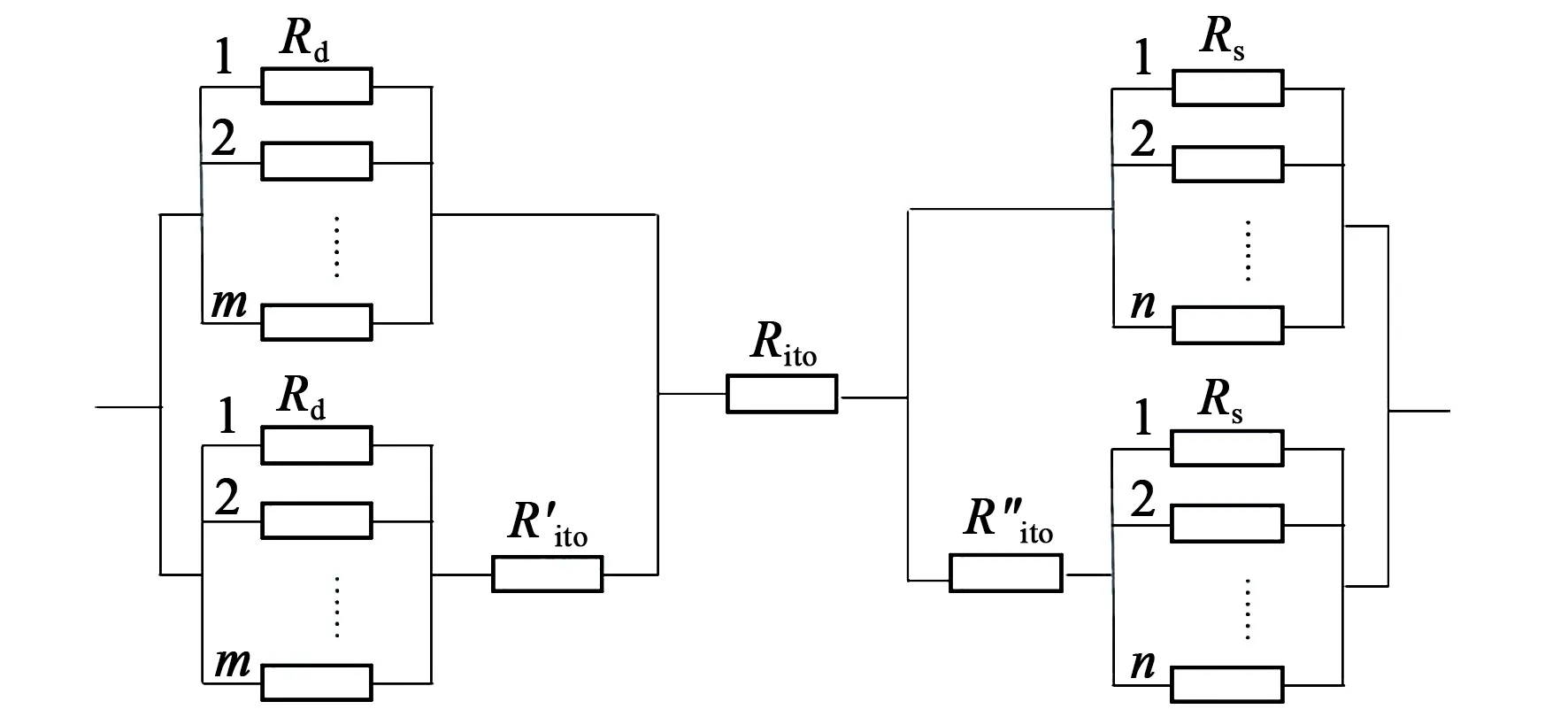
图7 双排孔竖向结构的过孔电阻等效电路图
依据电阻的串并联公式,双排孔竖向结构的过孔电阻为:
(5)
2.2.3 双排孔横向设计


图8 双排孔横向结构的ITO连接过孔电阻图形Fig.8 Pattern of the via hole resistance connected by ITO with double-row structure
同理,双排孔横向结构的过孔电阻等效电路图如图9所示。

图9 双排孔横向结构的过孔电阻等效电路图Fig.9 Equivalent circuit diagram of the via hole resistance with double-row structure
依据电阻的串并联公式,双排孔横向结构的过孔电阻为:
(6)

其他复杂类型过孔电阻的计算公式可以通过分析等效电路图同理得到。
3 结果与讨论
为了验证上述过孔电阻计算公式的准确性,我们需要计算出各种类型的过孔电阻阻值,然后与实测阻值进行相关性分析。Rd和Rs需要测量和拟合得到计算公式,ITO的方块电阻Rd以及过孔的尺寸信息可以通过直接测量得到。
3.1 深孔和浅孔的接触电阻计算
表1是用开尔文四线检测法测量一系列不同孔径的接触电阻阻值。由表中数据可知,随着孔面积的增加,深孔和浅孔的接触电阻均呈明显下降趋势。在孔面积相等的情况下,正方形孔与长方形孔接触电阻几乎一样,且浅孔的接触电阻远大于深孔接触电阻。玻璃中心位置ITO与金属的接触电阻均明显大于玻璃边缘位置,存在位置别差异。

表1 不同大小深孔和浅孔的接触电阻值
将孔面积的倒数与接触电阻值做线性拟合,深孔线性相关系数达到0.99以上,浅孔线性相关系数达到0.98以上,如图10所示。

图10 深孔(a)和浅孔(b)的接触电阻与孔面积的线性拟合曲线
由此,我们得到深孔和浅孔的接触电阻计算公式:
玻璃中心位置,Rd(Ω)= 670.97/S2+ 3.805,
(7)
玻璃中心位置,Rs(Ω)= 1831.1/S2-4.671,
(8)
玻璃边缘位置,Rd(Ω)= 536.77/S2+0.567 5,
(9)
玻璃边缘位置,Rs(Ω)= 1027.4/S2-3.541 3,
(10)
其中S为孔面积,单位μm2。
与此同时,我们对过孔进行了微观形貌表征和元素成分分析,如图11和图12所示。

图11 深孔和浅孔的扫描电子显微镜图(a)和聚焦离子束显微镜图(b)
从显微镜图片中可以看出,浅孔边缘非常光滑,而深孔边缘多一个小斜坡,这是由于深孔需要刻蚀PVX和GI两层绝缘层导致的。
栅极金属Cu上方还有MTD层,源漏极金属Cu上方没有其他膜层。结合图12的EDS结果可知,浅孔中心是ITO与Cu直接接触,深孔中心是ITO与MTD直接接触,深孔边缘是ITO与SiNx直接接触。因此ITO与金属Cu的接触电阻大小直接与孔的接触面积相关,与孔的形状无明显关系。这也证明了上述拟合公式的合理性。Cu工艺的这些结果与白金超等人研究的Al工艺过孔有着明显的区别。

图12 深孔和浅孔的EDS结果。(a)浅孔中心;(b)深孔中心;(c)深孔边缘;(d)测试点位。
由于Cu与ITO的电学接触性能不好,接触电阻较大,而MTD与ITO有较好的电学接触性能,接触电阻远小于Cu与ITO的接触电阻。故相同的孔面积下,深孔的接触电阻远小于浅孔接触电阻。
如果栅极金属不使用MTD,也采用与源漏极金属相同的膜层结构即MoNb/Cu,则可以推断在相同孔面积下,深孔和浅孔的接触电阻大小相当。
选择一片栅极和源漏极金属均为MoNb/Cu的样品进行接触电阻测试,测试结果如下:孔尺寸为11 μm×11 μm,玻璃中心位置,深孔接触电阻10.42 Ω,浅孔接触电阻10.39 Ω;玻璃边缘位置,深孔接触电阻4.18 Ω,浅孔接触电阻4.21 Ω。测试结果符合预期,证明了上述Cu工艺的微观分析结论的正确性。
3.2 ITO连接的过孔电阻计算
表2为26个ITO连接过孔的尺寸信息,统一进行编号。孔对数是指深孔和浅孔的个数,一个深孔和一个浅孔称为1对。表中均为单排孔结构,同一编号的过孔的深孔和浅孔数量相等,深孔和浅孔的孔尺寸相同。坡度角α=40°,GI和PVX的厚度分别为420 nm和400 nm,LF和W可直接量取,依据公式(3)可计算出表中的LR。
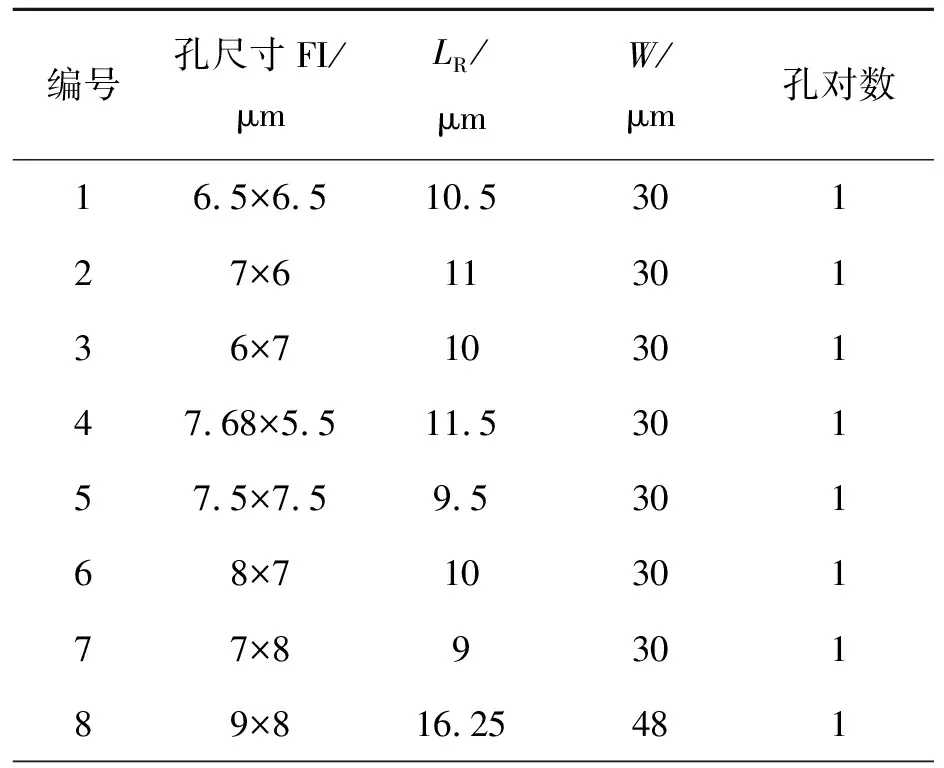
表2 ITO连接过孔的尺寸信息
依据表2中的孔尺寸可算出孔面积,通过公式(7)、(8)、(9)、(10)可计算出Rd和Rs。由于拟合的孔面积范围有限,Rs实际计算中有可能出现负值。R□可通过测量直接得到,玻璃中心和边缘位置分开测量,依据公式(2)和表2中的LR和W即可计算出Rito。最后,依据公式(4)即可模拟计算出过孔的电阻值,如表3和表4所示。
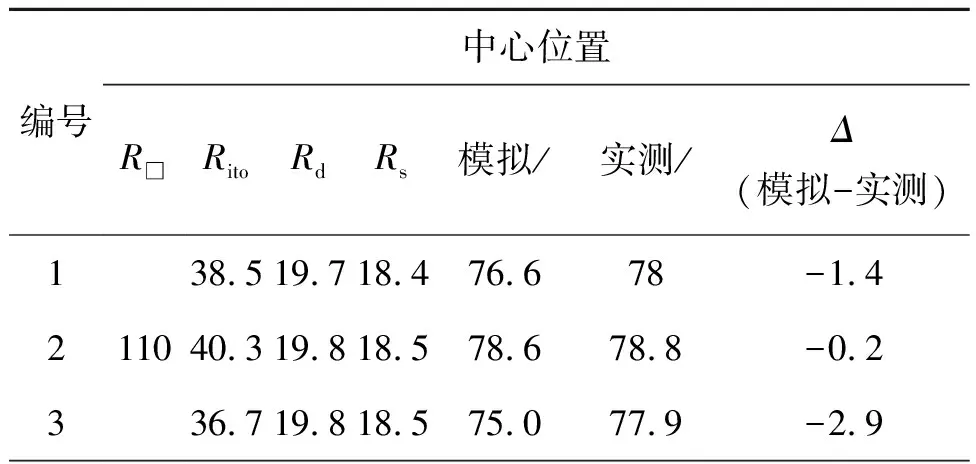
表3 玻璃中心位置ITO连接过孔电阻的模拟与实测结果

表4 玻璃边缘位置ITO连接过孔电阻的模拟与实测结果
从表3和表4中可以看出,模拟计算值和实测值匹配程度较好。对模拟值和实测值进行相关性分析,结果如图13。使用二元正态密度椭圆分析,模拟值与实测值均值偏小8 Ω,标准差相当,两者的线性相关系数达到0.96,证明了上述公式以及计算方法的可靠性。

图13 ITO连接过孔电阻模拟值与实测值的相关性分析
3.3 不同结构的过孔电阻
针对一些不同结构的过孔设计,这里选择若干组过孔电阻实测数据进行对比分析,给出一些设计建议。
3.3.1 孔两端正对与非正对设计
图14为两组单排孔正对与非正对设计的阻值对比。从图中可以看出,孔两端金属线正对与非正对设计对整体过孔电阻无影响,设计时可灵活采用。
3.3.2 ITO宽度问题
图15为两组ITO宽度不同的单排孔阻值对比。组内单孔尺寸和深浅孔间距均相同,只是ITO宽度即W不同。从图中可以看出,ITO宽的过孔(a)阻值明显比ITO窄的过孔(b)阻值小。这也说明ITO过孔电阻与ITO的宽度即W有关,与之前公式(2)一致。

图15 不同ITO宽度的过孔阻值对比。(a)ITO宽;(b)ITO窄;(c)中心位置阻值对比;(d)边缘位置阻值对比。
3.3.3 双排孔竖向设计
图16为3组竖向双排孔与单排孔的阻值对比。每组内包含4种过孔,组内单孔尺寸和深浅孔间距均相同,只是深浅孔的列数不同。从图中可以看出,竖向双排孔(a)与单排孔(b)没有明显的阻值差异。
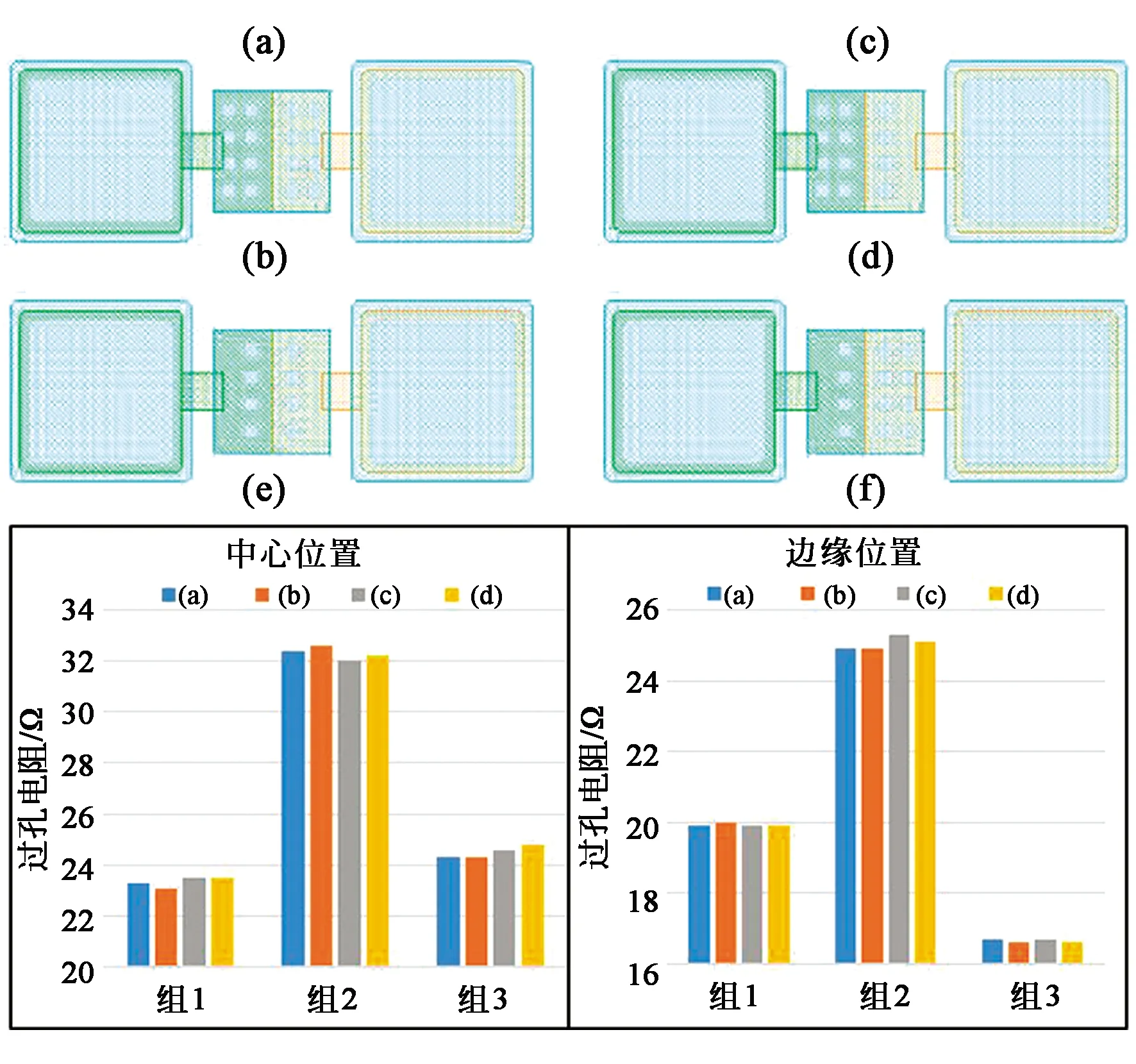
图16 竖向双排孔与单排孔的阻值对比。(a)双排深浅孔;(b)单排深浅孔;(c)双排深孔单排浅孔;(d)单排深孔双排浅孔;(e)中心位置阻值对比;(f)边缘位置阻值对比。

3.3.4 双排孔横向设计
图17为两组横向双排孔与单排孔的阻值对比。每组内包含4种过孔,组内单孔尺寸和深浅孔间距均相同,只是深浅孔的行数不同。横向双排孔(a)的阻值约等于单排孔(b)阻值的1/2。

图17 横向双排孔与单排孔的阻值对比。(a)双排深浅孔;(b)单排深浅孔;(c)双排深孔单排浅孔;(d)单排深孔双排浅孔;(e)中心位置阻值对比;(f)边缘位置阻值对比。
从公式(4)和(6)可以看出,横向双排孔的阻值等于单排孔阻值的1/2,与实测值基本一致。同时,(d)排列的过孔电阻与横向双排孔阻值相当。说明增加浅孔的行数对过孔电阻没有明显贡献。故在双排孔横向设计时建议采用两行深孔一行浅孔。
3.4 过孔电阻与击穿电流
我们还进一步探索了过孔击穿电流与过孔阻值之间的关系。我们测量了42组过孔电阻和它的击穿电流值,分别用幂函数和焦耳公式进行拟合,结果如图18所示。

图18 过孔电阻与击穿电流的关系。(a)幂指数拟合;(b)焦耳公式拟合。
过孔烧毁通常被认为是过孔电阻产生的焦耳热过大导致过孔结构发生破坏导致的,按照焦耳定律就是过孔电阻与击穿电流的倒数存在二次方的关系。从图18(a)幂函数拟合情况来看,拟合出的幂指数为-1.327,介于1和2之间,相关系数达到0.98。按照图18(b)焦耳定律拟合的函数,电流倒数的平方为非负数,则过孔电阻不低于17.68 Ω,这显然是不合理的,且相关系数不到0.96。因此幂函数关系更为显著,推测过孔电阻与击穿电流之间可能存在着一次方和二次方关系的综合影响。我们可通过这个幂函数公式推算出过孔的击穿电流大小。
4 结 论
本文首先研究了ITO接触电阻并拟合得到了深孔和浅孔的接触电阻计算公式,同时阐明了铜工艺下的过孔接触电阻的不同规律,MTD金属能够明显改善铜与ITO的接触电阻。然后对ITO连接过孔电阻进行详细的分解,推导了多种结构过孔电阻的计算方法,并利用实测数据验证了计算方法的可靠性,相关系数达到0.96。针对不同结构的过孔,通过实测数据对比分析,提出了一些过孔相关的设计建议:过孔两端金属正对与非正对设计对电阻大小没影响;ITO宽的过孔电阻较小;双排孔竖向设计时深孔或浅孔列数的增加对电阻基本没贡献;双排孔横向设计时浅孔行数的增加对电阻基本没贡献。最后,探索了过孔电阻阻值与击穿电流的幂函数关系,幂指数为-1.3,相关系数达到0.98。自此,我们建立起了一整套可定量计算过孔电阻及其击穿电流的方法,为合理设计过孔提供了依据。
