岩石爆破损伤中水不耦合系数变化效应研究

李 卓，雷兴海，李 恒，张智宇，徐 斌

(1.昆明理工大学 公共安全及应急管理学院，昆明 650093； 2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，昆明 650093； 3.贵州大学 矿业学院，贵阳 550025； 4.昆明理工大学 国土资源工程学院，昆明 650093； 5.攀钢集团攀枝花新白马矿业有限责任公司，四川 攀枝花 617209)

水不耦合装药是在炮孔内填充水介质，这对爆炸冲击波产生一定缓冲作用，可有效减小爆炸冲击波作用于孔壁的峰值压力从而提高爆破效率。目前，大量国内外学者对不耦合装药的作用机理、炮孔峰值压力及高效的不耦合系数范围等开展了一定理论计算、现场试验以及数值模拟的相关研究。

洪志先等[1]通过有限元软件LS-DYNA对单孔不耦合装药的数值模型在不同的起始应力状态下进行了模拟计算，通过对数值模拟结果分析得出，当不耦合系数大于2时，不耦合系数对各质点峰值压力和峰值速度的影响逐渐减小。潘强等[2]研究单孔不耦合装药的条件下，利用岩石损伤分布特征公式得出了在爆破应力波和准气态作用下的特征公式，结果表明衰减速率不随不耦合系数减小而减小。倪文婧[3]利用AUTODYN-2D比较了不耦合系数、不耦合介质和炸药类型对爆破效果的影响。研究结果表明在径向不耦合装药条件下的炮孔峰值压力明显低于径向耦合装药条件下的炮孔峰值压力。朱红兵等[4]推导和分析了在轴向不耦合装药条件下爆轰产物在爆破孔内的运动及其相互作用过程，阐明了轴向不耦合装药的作用机理。杜虎[5]以LS-DYNA为分析软件，研究了不耦合装药系数对粉碎圈的影响，得出不耦合装药系数与粉碎圈等效圆柱半径值及粉矿数量成负相关变化。宗琦等[6]以LS-DYNA为分析软件，研究了当不耦合系数为1.68时同心和偏心不耦合装药爆破模型的峰值出现时间和裂隙贯穿效果，研究表明同心不耦合装药和偏心不耦合装药的峰值应力出现时间的分布规律显著不同，前者装药结构相对于后者装药结构的裂隙贯穿效果更好。瑞典的LANGEFORS[7]发现爆破裂纹的数目并不会随着不耦合系数的增大而增大，当其等于1.67时，其裂纹总长及其平均总长均达到峰值。米中阳[8]分析了水孔爆破理论、水耦合介质理论和空气不耦合介质理论。结果表明，水介质下的能量传递效率明显高于空气，因此得出水耦合介质的爆破效果优于空气。考虑到爆破试验成本高昂、耗时长，采用数值分析软件LS-DYNA来模拟岩石爆破损伤仍是一种行之有效的方法。

大红山铜矿巷道掘进爆破时，需要对预保留岩体的破坏程度进行控制，从而达到合理预估和改善爆破效果的要求，当前研究表明水介质对不耦合装药爆破优于耦合装药爆破的效果，但对水介质不耦合爆破下其损伤规律研究较少，故本文基于LS-DYNA及JHC本构模型，基于损伤变量的角度对不同水介质不耦合装药系数K下岩石中单孔爆破进行模拟分析。分析不同K值对爆破应力波衰减的规律及比较不同K值的岩石爆破损伤的范围及损伤度；其次探究爆破体积及扩腔半径比随K值增大的变化规律以预期获得对实际工程有参考价值的结论。

1 不耦合装药时水介质中冲击波的产生和传播

采用CJ爆轰理论模型对爆轰产物参数进行计算，炸药、爆轰产物和水介质三者的分界面一直保持接触，在分界面处速度满足连续条件，基于爆轰产物等熵方程及声速公式，得出交界面速度为[9-12]：

(1)

式中：De为炸药爆速。

水介质中初始冲击波波后参数在炸药与水介质分界面满足压力、质点速度连续性条件，可以表示为：

Px=Pwx

(2)

ux=uwx

(3)

式中：Pwx和uwx分别为水介质中透射冲击波波后压力与质点速度。

强冲击波作用下水介质的状态方程为(Pw>2 500 MPa)

(4)

式中：Pw和ρw分别为水介质冲击波波后压力、密度；ρw0为水介质的初始密度；A、B为常数，通常取A=425 MPa，B=6.29。

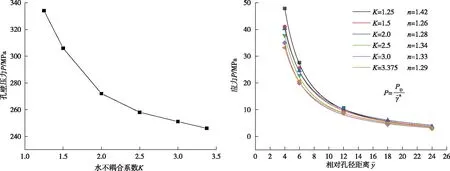
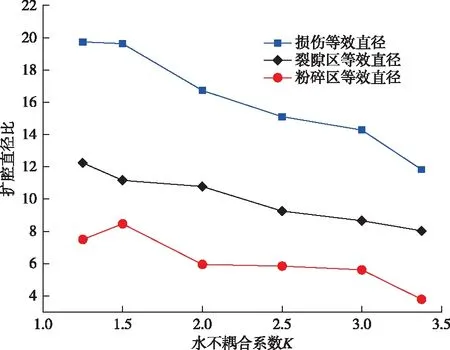
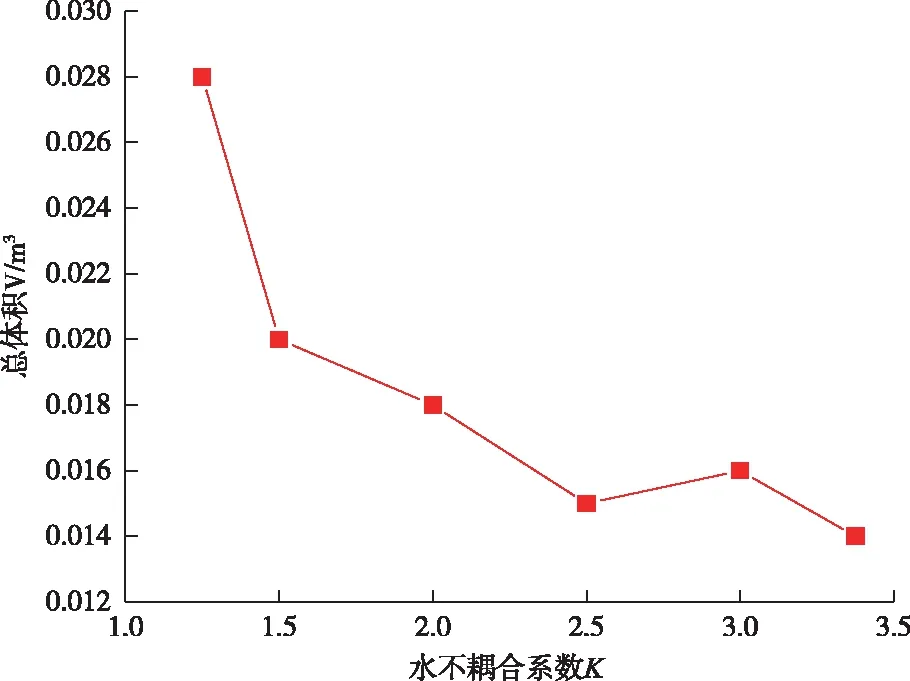
中等强度冲击波作用下水介质的状态方程为(100 MPa

(5)

式中：A和B为常数，通常取A=304.5 MPa，B=7.15。

根据水介质中冲击波的质量、动量守恒方程可得：

(6)

式中：Pw0为水介质初始压力，与冲击波波后压力相比很小，因此忽略不计；vw0和vwx分别为水介质的初始比容和水介质初始冲击波波后比容。

由式(5)和(6)可得水介质初始冲击波波后压力Pwx和质点速度uwx。

水介质中的初始冲击波传播一定距离后作用于孔壁，其衰减规律如下式所示：

(7)

(8)

根据孙磊等[13-15]的研究，考虑轴向装药系数ls对孔壁压力峰值的影响，得出水介质不耦合装药爆破孔壁压力峰值如式(9)所示：

(9)

2 爆破漏斗数值模拟试验

2.1 模型建立

为研究水介质不耦合装药K值变化对围岩爆破损伤的影响，利用LS-DYNA软件模拟空气不耦合装药与水不耦合装药对围岩爆破损伤影响[16]。考虑到大红山模型几何相似比为CL=1∶18，因此，将岩体简化为二维平面模型，具体的模型尺寸设置为1 m×1 m，炮孔直径分别为1、1.2、1.6、2.0、2.4、2.7 cm，对应的水介质不耦合装药时K值为1.25、1.5、2.0、2.5、3.0及3.375，药包直径为0.8 cm，模型边界设置为无反射边界。对平面模型进行网格划分，围岩、炸药、水介质均采用单元SOLID 164，且炸药及水介质采用欧拉网格建立相对应模型，岩石材料采用拉格朗日网格建立模型，模型划分为16 348个单元。

2.2 本构与材料参数

本文数值模拟采用LS-DYNA显示动力分析有限元软件，模型选取3种材料，炸药材料本构选择MAT_HIGH_ EXPLOSIVE_BURN，其状态方程是EOS_JWL；水介质材料本构选取具有代表性的MAT_NULL，其状态方程表述为EOS_GRUNEISEN，具体参数见表1；为了能清晰认识到岩石内部损伤，本文采用能够更好体现压缩及拉伸损伤的HJC岩石本构模型，其具体参数整理如表2。炸药及水材料在数值模拟中通常可视为流体，但炸药与空气之间具体是通过共节点方式来保证炸药能量传递，而岩石可视为固体，流固体之间则采用流固耦合方式，通过关键字CONSTRAINED_LAGRANGE_IN_SOLID来实现，最终保证爆炸能量在流固体之间相互传递。

表1 炸药参数

表2 HJC模型参数

3 模拟试验及分析

为更准确研究系列水不耦合系数装药下最优爆破损伤效果，对岩石内部应力波衰减过程、损伤范围及损伤度随爆心距变化等内容进行分析。

3.1 岩石损伤内部应力波演化规律

现提取不同K值下相同位置的孔壁压力及应力，并分析应力衰减过程。

据图1可以清晰看出孔壁压力随着K值变化的规律及爆炸应力波在不同K值下随爆心距的变化规律。由于从水层透射的应力波不断压缩岩石介质，造成应力峰值衰减，进一步分析如下。

因为不同厚度水介质的作用，会产生缓冲效果从而形成削峰作用，其影响表现为随着不耦合系数增加，炮孔峰值应力P呈降低的趋势。将其余K值与K=1.25时孔壁上峰值压力对比分析，可以发现，K=2时孔壁上峰值压力约下降了19%，K=3.0的炮孔壁的峰值压力下降了约29%，K=3.375的炮孔壁的峰值压力下降了约31%，这表明当K=2.0后，炮孔壁峰值压力不再显著降低，这与公式(8)相符合。

不同K值下的应力波衰减规律表明：随着K值越大，其衰减时间也相对地延长，研究结果还发现水介质不耦合装药K值为1.5时，衰减指数n为1.26，此时应力波与岩石破碎相匹配的应力持续时间最长。

图1 不同K值下孔壁压力及应力波衰减规律Fig.1 Attenuation law of hole wall pressure and stress wave under different K values

3.2 岩石损伤范围随着不耦合系数变化规律

为了清晰观察水介质不耦合装药不同K值下岩石内部损伤演化规律，提取整理不同K值下对应的损伤云图形成图2。

图2 不同装药不耦合系数下岩石内部损伤演化Fig.2 Internal damage evolution of rock under different charge decoupling coefficients

从图2可以看出，水介质不耦合装药时不同K值对岩体损伤的影响规律，在爆破应力波作用下，随着爆心距离增加，模型的损伤范围与程度降低；损伤的扩展形式呈放射状，具体分析如下：

根据炸药爆破后岩体的受力分布情况以及岩石的动态抗压强度[17]，可把损伤因子大于0.9的区域作为压碎区，损伤因子在0.19～0.9区域作为裂隙区，损伤因子为0～0.1的区域作为弹性区[18]。本文用损伤等效直径比(损伤范围等效直径/药卷直径)来分析损伤范围变化规律，研究结果表明，随着不耦合系数的增加，损伤等效直径比呈现减少趋势，在K值为1.25时损伤直径比值最大，其值为19.74，此后随着K值进一步增加，在应力峰值降低及衰减速度增加的综合影响下，损伤范围呈减少趋势，这也满足峰值压力及应力波的衰减规律。

图中不耦合系数K在1.25～3.375范围内，裂隙区损伤变化曲线呈左高右低形状，且呈下降趋势；K在1.25～2.3.375范围内，粉碎区范围先增加至峰值(K=1.5)后逐步减少呈整体下降趋势。其原因是，在K<1.5时孔壁应力波具有一定强度，且此时应力波衰减速度最慢，此后随着K值增加，孔壁峰值应力下降，且衰减速度明显提升。

4 现场试验结果

4.1 现场试验准备

由于模型试验能较好反映原型的特征，为进一步开展实际中水介质不耦合装药不同K值下岩石损伤变化，开展相关模型试验研究，模型尺寸为1 m×1 m，在云南省安宁化工厂制作并养护28 d，同时对混凝土试件的多项力学物理参数进行测量，本试验试件相关物理力学参数测量结果为：密度ρ=1.647 g/cm3；纵波速度C=2 315 m/s；弹性模量E=6 GPa；单轴抗压强度P=8.35 MPa；炸药采用黑索金，设计单孔装药q=3.5 g，爆破时由8号瞬发电雷管引爆，所用的黑索金参数具体为：密度ρ=1.69 g/cm3，爆速v=8 310 m/s，爆热Q=5.4 MJ/mol。

4.2 现场结果及分析

关于爆破漏斗扩腔体积值确定，本试验采用物理测量方法，可测量漏斗底部面积以及漏斗高度等值，进而通过数学方法估算出漏斗体积值，其测量过程如图3所示，所得数据整理成表3。最终通过以上数据开展不同K值的爆破损伤效果分析。

图3 不同水不耦合系数下损伤范围变化规律图Fig.3 Variation curves of damage range under different water uncoupling coefficients

表3 不同K值爆破漏斗试验结果

图4 爆腔体积测量过程Fig.4 The measurement process of cavity volume

4.3 爆破扩腔体积及爆腔扩腔直径比

将表3中现场爆破扩腔直径比及漏斗体积数据绘制成图5，进一步分析如下：

图5 爆破扩腔直径比及漏斗体积随K值变化趋势Fig.5 Variation trend of diameter ratio of blasting cavity expansion and funnel volume with K value

从图5可知，爆破漏斗扩腔直径比随水不耦合系数增加的变化规律基本上表现为：随着水不耦合系数增大，扩腔直径比值呈先增大后减小趋势，随着不耦合系数增加，爆破扩腔能力减小。在1.25

5 结论

通过理论分析、数值模拟分析及混凝土模型单孔爆破试验，选取不同的K值进行混凝土模型和数值模拟单孔爆破试验，分析水介质不耦合装药时K值变化对岩石破坏的影响规律，结果表明：

1)理论分析指出：当不耦合系数K<2和K>2时，水介质中冲击波的传播和衰减具有不同的规律。根据水介质中冲击波与孔壁的相互作用关系，得出与炸药类型、水介质和岩石种类相关的孔壁压力峰值计算公式。

2)数值模拟进一步分析得出，当K<2时，随着K值的增加，孔壁峰值压力显著降低；当K>2时，随着K值的增加，孔壁峰值压力降低速度小于前者；水不耦合系数为1.5左右时，爆炸应力波衰减速度最慢，其衰减系数n为1.26，爆破压应力能保持一定强度，且在岩体中传播时间相对长。

3)通过对LS-DYNA模拟单孔爆破试验结果分析，水介质不耦合装药系数为1.5时，粉碎区范围较大，而裂隙区范围相对小，即此装药系数下使得爆破损伤效果比较理想。

4)通过模型实验得出爆炸所产生的爆破漏斗体积值及爆破扩腔直径比随着水不耦合系数的增加呈现减少的趋势。

5)后续的研究中，在进行混凝土模型单孔爆破试验时，不耦合系数K的取值需进一步细化，浇筑混凝土模型的过程中，可以在混凝土内部预埋岩石应变片，借助超动态应变仪和声波监测仪，检测孔壁的峰值压力和混凝土内部的损伤分布，能更加准确地得出水介质不耦合装药时岩石孔壁峰值压力及内部的损伤规律。