二次函数最值题型的归类及突破
2022-01-27王军南
◎王军南
(甘肃省庆阳市镇原县城关初级中学,甘肃 庆阳 744500)
结合自身教学实践,对二次函数最值问题进行汇总与分析认为二次函数最值题型包括:定轴定区间最值问题、定区间动轴最值问题、定轴动区间最值问题、模型类最值问题、几何图形类最值问题、实际问题类最值问题.但无论哪种题型,都需要应用到二次函数的性质,必要情况下需要根据习题创设的情境进行分类讨论,因此,在学习的过程中应注重切实打牢基础,熟练掌握不同题型的解题思路,把握相关的解题细节,尤其保证考虑问题的全面性.
一、定轴定区间类最值问题
相对来说定轴定区间类的习题难度不大.解题时根据题目中给出的二次函数解析式,结合二次函数图像,确定对称轴与给定区间之间的关系,结合二次函数图像性质不难求解出对应的最值.当然部分习题可能不会直接给出二次函数的解析式,解题时需要根据题干中的已知条件先确定其解析式,而后结合二次函数的对称轴以及给出的自变量范围求出对应的最值.如下题:
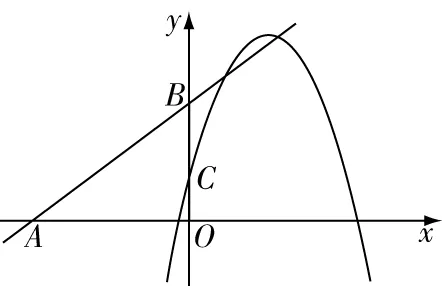
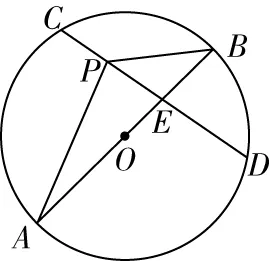
例已知二次函数y=x2+bx+c的图像经过坐标原点O和A(7,0),直线AB交y轴于点(0,-7),动点C(x,y)在直线AB上,且-1 A.有最小值9 B.有最大值9 C.有最小值8 D.有最大值8 解题思路该习题没有直接给出二次函数的解析式,但是给出其经过的两个点,此时可采用待定系数法求出其具体的解析式,而后画出相关的辅助图形,找出CD的长与自变量的函数关系.确定函数与对称轴的大小关系,便可求出对应的最值. ∵二次函数y=x2+bx+c的图像经过坐标原点O和A(7,0). ∴c=0,49+7b=0,解得b=-7 ∴二次函数为y=x2-7x 又∵直线AB交y轴于点(0,-7),设过AB的直线方程为y=kx+b,将AB两点坐标代入得到y=x-7,则C(x,x-7),D(x,x2-7x) ∴CD=x-7-(x2-7x)=-(x-4)2+9.可知其表达式为二次函数,其二次函数的对称轴为直线x=4,又∵-1 解题点评二次函数的定轴定区间最值问题是学生学习二次函数时最先接触的问题.解题时既需要确定二次函数的对称轴与区间之间的关系,又需要明确抛物线的开口方向,在此基础上找到取得最大值的点,将其代入到二次函数中进行计算即可. 解答定区间动轴问题,需要根据题目创设的情景进行分类讨论.讨论的思路为:对称轴在区间的左侧、对称轴在区间内部、对称轴在区间的右侧.当然要求解其最值还需要根据二次函数图像的开口方向,确定其最大值还是最小值.需要注意的是,当对称轴处在区间内部时,在其顶点处取得最大值和最小值.另外,在确定最后的结果时,需要整合各种满足题意的结果.如下题: 例当-2≤x≤1,二次函数y=-(x-m)2+m2+1有最大值4,则m的值为( ). 解题思路习题中的自变量范围为-2≤x≤1,二次函数图像的开口方向向下.明确这一点后便可按照对称轴从左到右的顺序进行分类讨论. ∵二次函数y=-(x-m)2+m2+1,则其对称轴为直线x=m,顶点为(m,m2+1). (3)当m>1时,二次函数图像对称轴在给定区间的右侧,则当x=1时取得最大值.代入可得4=-(1-m)2+m2+1,解得m=2. 解题点评定区间动轴类最值问题在初中数学中较为常见.该类问题主要考查学生对二次函数性质的认识与灵活应用程度.因为二次函数的对称轴是不确定的,所以可将对称轴按照从左到右的顺序,考虑每一种可能的情况.需要注意的是在计算的过程中应注重对相关参数进行合理的取舍. 定轴动区间最值问题和定区间动轴问题类似,均需要进行分类讨论.一般情况下分类讨论需要分三种情况.当然也有部分习题较为特殊,需要根据已知条件先确定自变量范围,找到其中的规律,便可减少分类讨论的情况.授课中为使学生具体问题具体分析,避免思维定式的干扰,应注重为学生多讲解相关的习题,使其掌握不同习题的特点以及对应的解题思路,避免在解题中走弯路,如下题: 例二次函数y=-(x-1)2+5,当m≤x≤n,且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( ). 解题思路解答该习题不要轻易动笔,应充分挖掘隐含条件,以降低解题的复杂度.由题目中m≤x≤n,且mn<0,便可判断出m、n和的大小关系,即,m<0,n>0.解题时只需要判断n和1的大小关系即可. (1)当m≤x≤n<1,由二次函数性质可知,x=m时取最小值,即,2m=-(m-1)2+5,整理解得m=2(舍去)或m=-2.当x=n时取得最大值,2n=-(n-1)2+5,整理解得n=2(舍去)或n=-2(舍去). 解题点评定轴动区间类最值问题区间是确定的,因此在讨论其最值时要认真审题,确定是求解最大值还是最小值,而后将区间按照一定的顺序移动,结合对称轴和区间的关系,抛物线的开口方向进行解答. 二次函数最值问题情境复杂多变,解题思路不尽相同.针对以二次函数为背景,求解两个线段之和最小值的习题,常采用模型法,例如将军饮马模型,通过点的对称,找到点的具体位置,运用几何知识能很快地求解出最值,因此在解题过程中为少走弯路,提高解题效率,应提高学生的模型应用意识,通过联系所学的模型,迅速地找到解题的切入点.如下题: 例如图1所示,已知直线y=kx+b(k,b为常数)分别和x轴,y轴交于点A(-4,0),B(0,3),抛物线y=-x2+4x+1与y轴交于点C,点E在抛物线的对称轴上移动,点F在直线AB上移动,则CE+EF的最小值为( ). 图1 A.2 B.4 C.2.5 D.3 解题思路习题要求解两个线段之和的最小值,先考虑到运用“将军饮马”模型,找到C点的对称点,因C点在抛物线的图像上,其对称点也在抛物线的图像上,且两点关于抛物线的对称轴对称.意识到这一点后,习题也就不难解答. 如图2,设点C关于抛物线对称轴的对称点为C′,由对称性可知CE=C′E.则CE+EF=C′E+EF,要想其值最小,则只需C′、E、F三点在一条直线上且其所在直线和直线AB垂直. 图2 解题点评解答二次函数模型类最值问题时应通过审题确定习题考查的是哪一种模型,模型中涉及哪些参数,题干中给出了哪些参数,还需要求解哪些参数等,而后运用所学求解出相关线段的长以及坐标,确定最值对应的参数. 解答几何图形内最值问题时常根据已知条件设置相关参数,构建对应的函数,借助函数的性质进行解答.其中构建二次函数求解图形类最值类问题时既需要灵活运用所学的几何知识,包括三角形全等、三角形相似、等腰三角形、圆的相关性质等,找到相关参数之间的内在联系.构建二次函数时为保证求解最值问题的正确性,应注重找到正确的自定义范围,结合二次函数性质计算出最终结果. 例如图3,已知圆O的半径为3,弦CD=4,A为圆O上不与点C、点D重合的一动点,连接AO并延长交CD于点E,交圆O于点B,P为CD上一点,当∠APB=120°时,AP·BP的最大值为( ). 图3 A.4 B.6 C.8 D.12 解题思路习题要求两个线段乘积的最大值,结合所学不难联想到三角形相似的性质总“两三角形相似,对应边成比例”,可将其转化为两条线段的乘积形式.同时考虑到求最值,需要构建对应的函数.认识到这些内容,便不难找到解题的思路. 如图4,延长BP交圆O于点F,连接AF、CF、BD,∵∠APB=120°,∴∠APF=60°,又∵AB为圆O的直径,∴∠AFB=90°,∴∠FAP=30°,∴AP=2PF,∴AP·BP=2PF·BP;由圆周 角定理可得∠FCP=∠PBD,又∵∠CPF=∠BPD,∴△CFP∽△BDP,∴CP/BP=FP/DP,PF·BP=CP·DP,设CP=x,∴DP=4-x(0 图4 解题点评求解几何图形类最值问题不仅需要灵活运用所学的几何知识求解出相关参数包括线段、角度、点的坐标等,而且需要结合已知条件合理设出相关参数,尤其当将问题转化为二次函数问题时应注重通过配方法确定其对称轴,结合自变量范围进行解答. 二次函数与人们的生产生活有着密切的联系,在解决实际问题中有着广泛的应用,尤其在求解实际问题中的最值问题时,使用二次函数可获得事半功倍的效果.运用二次函数实际问题的最值问题,常出现在初中数学各类测试中.解题中,应结合自身经验把握相关参数之间的内在逻辑关系,明确自变量与因变量,构建对应的二次函数,运用二次函数性质进行探讨. 解题思路该题以人们生活中的产品销售为背景进行设问.通过审题可知其涉及较多的参数,准确找到参数之间的关系是解题的关键,因此既需要认真审题,又需要应结合自身的生活以及解题经验,理清解题的思路. 解题点评运用二次函数求解的实际问题类的最值问题,关键如何构建正确的二次函数模型.解题时应把握以下两点:其一,认真审题,提炼出有用信息.其二,根据题干描述以及自身生活经验,通过合理的抽象确定参数间的函数关系,尤其针对不同自变量范围下对应不同的函数关系时应注重分类讨论. 二次函数最值问题情境灵活多变,是各类测试以及中考的热门考点.部分学生因分类讨论的意识不强或者未掌握分类讨论的技巧,在解题的过程中非常容易出错.教师在授课中需帮助学生掌握该类题型,在对二次函数基础知识深入讲解的基础上对最值问题分门别类,并讲解相关的解题思路,尤其在课堂上讲解经典例题时,要与学生一起剖析解题过程,使学生留下深刻的印象,布置专题训练习题,要求其在课下解答,从而达到及时巩固所学,积累丰富的经验,掌握相关的技巧的目的.二、定区间动轴类最值问题




三、定轴动区间类最值问题



四、模型类最值问题

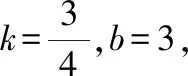
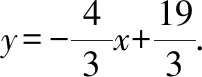
五、几何图形类最值问题
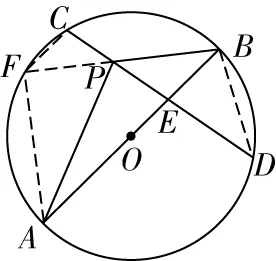
六、实际问题类最值问题
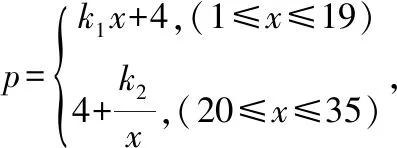
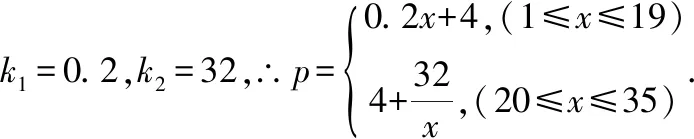
七、总 结
