二次函数教学实用方法——二次函数的复习攻略

◎张 跃

(四川省眉山市东坡区太和镇悦兴初级中学，四川 眉山 620039)

翻阅所有版本的教材，可以发现二次函数的内容都是从特殊二次函数到一般二次函数.利用逆向思维，复习时我们不妨从一般到特殊，打乱原有不变的教学模式，来个大反转.

二次函数的图象都是抛物线，视二次项系数a>0还是a<0分为开口向上和开口向下两种.

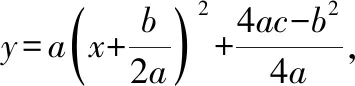
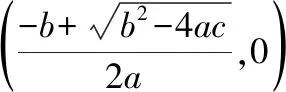
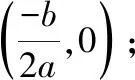
当判别式Δ=b2-4ac<0时，抛物线与x轴没有交点.

特殊情况：

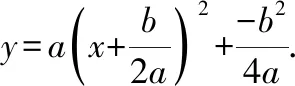
(2)当b=0时，二次函数为y=ax2+c，配方为y=a(x+0)2+c.图象顶点为(0,c)；对称轴为直线x=0;与y轴交点为(0，c).

(3)当b=0且c=0时，二次函数为y=ax2，配方为y=a(x+0)2+0.图象顶点为(0,0)；对称轴为直线x=0;与y轴交点为(0，0).

也就是说，所有的特殊情况都符合一般情况的公式，不必再分情况一一讲解，既节省了时间，也提高了学习效率，何乐而不为呢？

若b=0，则抛物线与y轴只有一个交点(0，c)，此时对称轴为直线x=0，则在y轴左侧和右侧找到一对对称点即可.

抛物线的雏形形成，进行延伸即得抛物线草图.

有了草图，在对称轴两侧根据图象走势便可得到图象的性质.

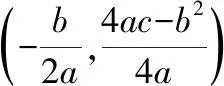
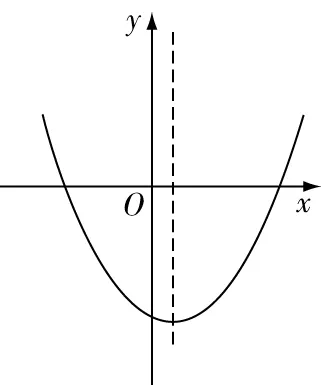
图1

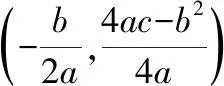
图2

这说明，所有的特殊情况都包含在一般情况中，掌握了一般情况，特殊情况勿需一一赘述，进而起到事半功倍的效果.

说到底，二次函数的图象归结为一条对称轴，三个点，这样，草图的绘制很快完成，有了草图，便可以根据草图得出开口向上或向下、函数的增减性等.当然，配方是基础，只有正确且快速地配方，才能迅速准确地作答.

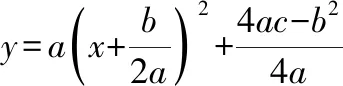
对于二次项系数a的作用，可概括为两点：一是a的正负决定抛物线的开口方向，二次项系数a>0，开口向上；二次项系数a<0，开口向下.二是a的绝对值决定抛物线的开口宽窄，a的绝对值越大，函数值y变化越快，坡越陡，开口越窄；a的绝对值越小，函数值y变化越慢，坡越缓，开口越宽.

c的作用是决定抛物线与y轴交点的纵坐标.当c=0时，抛物线与y轴交于原点；当c>0时，抛物线与y轴交于正半轴；当c<0时，抛物线与y轴交于负半轴.

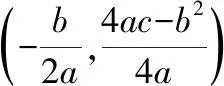
判别式Δ=b2-4ac的作用就是在函数值y=0时，判别一元二次方程ax2+bx+c=0的实数根的对应情况.

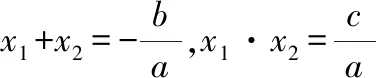
几种二次函数的图象特征归纳如下：

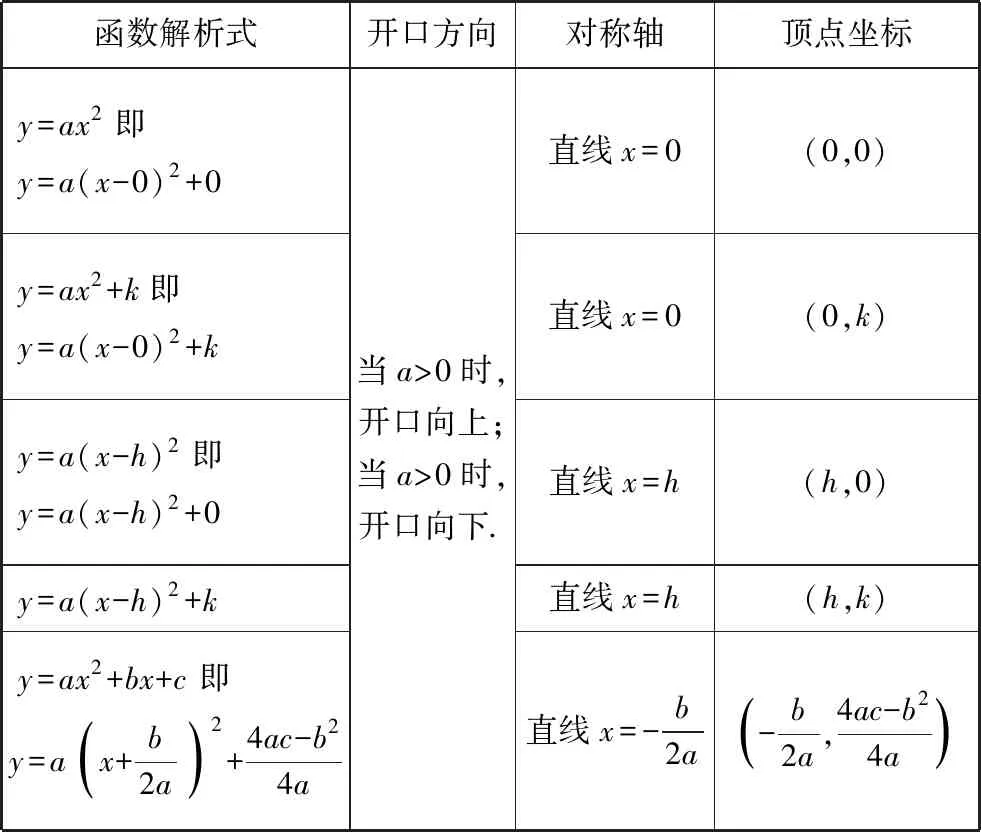
函数解析式开口方向对称轴顶点坐标y=ax2即y=a(x-0)2+0y=ax2+k即y=a(x-0)2+ky=a(x-h)2即y=a(x-h)2+0y=a(x-h)2+ky=ax2+bx+c 即y=a(x+b2a)2+4ac-b24a当a>0时,开口向上;当a>0时,开口向下.直线x=0(0,0)直线x=0(0,k)直线x=h(h,0)直线x=h(h,k)直线x=-b2a-b2a,4ac-b24a()

求抛物线y=ax2+bx+c(a≠0)的对称轴和顶点坐标通常有三种方法：配方法、公式法、代入法，这三种方法都有各自的优缺点，所以应根据实际灵活选择和运用.

例1如图3，二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，有下列结论：

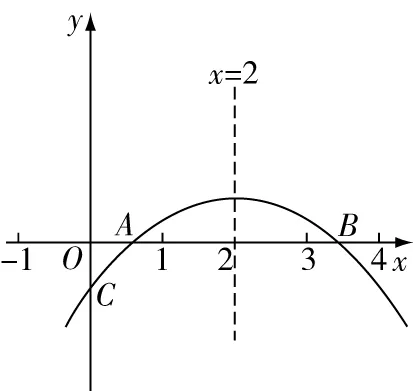
图3

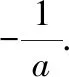
其中正确的结论有( ).

A.1个 B.2个 C.3个 D.4个

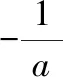
例2函数y=ax+b和y=ax2+bx+c(a≠0)在同一直角坐标系内的图象大致是( ).

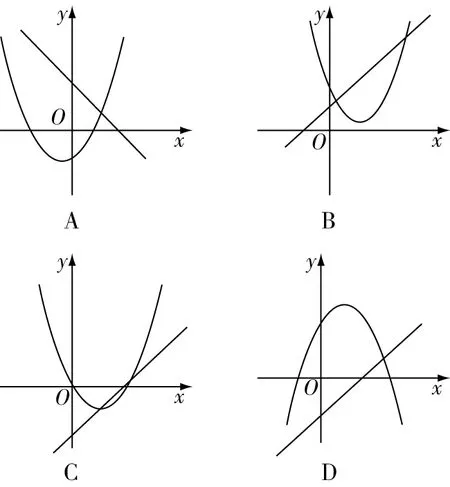
分析因为a≠0，所以分a>0，a<0两种情况来讨论两函数图象的分布情况.如果a>0，那么函数y=ax+b的图象必经过第一、三象限，函数y=ax2+bx+c的图象开口向上，所以D不正确.如果a>0，b>0，那么函数y=ax+b的图象与y轴的交点在y轴的正半轴上，函数y=ax2+bx+c的图象的对称轴在y轴的左侧，所以B不正确.如果a>0，b<0，那么函数y=ax+b的图象与y轴的交点在y轴的负半轴上，函数y=ax2+bx+c的图象的对称轴在y轴的右侧，所以C正确.如果a<0，那么函数y=ax+b的图象必经过第二、四象限，函数y=ax2+bx+c的图象开口向下，所以A不正确.因此答案为C.

结论在同一直角坐标系中研究两种函数图象的分布情况，待定系数a，b必须满足一致性，也就是说，讨论a，b的符号一致性是解决本题的关键.a，b的符号不但决定了一次函数图象的分布情况，还决定了抛物线的开口方向和对称轴的位置.

总之，二次函数要过关，配方扎基础，要知性质需画图，画图只需画草图，牢记三点画草图，有了草图性质全了知.反之，已知草图论，判断a,b,c的相关情况便容易得多.