中职数学项目引导和任务驱动教学法的实践探究

◎闫晓辉

(辽宁省凌源市职业教育中心，辽宁 凌源 122500)

前 言

现阶段，新课标对中职院校的数学教学提出的标准以及要求有了明显提升.然而，在中职院校的数学教学当中，亟待解决的一个问题是中职生普遍缺少学习兴趣，课堂教学效果不高，进而难以取得预期效果.此种情况之下，数学教师可以运用项目引导和任务驱动的方法，对实际教学期间的一些问题加以解决.因此，在中职院校数学教学当中，对项目引导以及任务驱动教学法的实践运用进行探究具有重要意义.在以往的中职数学教学中，项目引导和任务驱动教学法的应用仍存在一些需改进之处，如任务设计不够灵活多变，没有真正地满足学生的学习需求，课堂给予学生的学习时间不多，学生得不到良好的学习指导，从而影响学习质量.本文主要研究项目引导和任务驱动教学法在应用过程中的注意事项和具体方法.

一、关于项目引导和任务驱动教学法的概述

实际上，项目引导和任务驱动教学法指的就是把教师当作主导，把学生当作主体，把项目当作主线，在一个或者几个任务当中融入新知识，通过任务促使中职生对新知识进行学习以及探究，让其对新技能进行掌握.具体而言，教师按类把某门课程分为多个项目，项目中还包含一个或多个任务，促使中职生通过完成某个或者某些任务完成相应项目，进而完成相应的教学目的.此种方法非常容易实施，这是因为以下几点.第一，教师在实际教学当中对任务驱动法加以运用，在中职生初步认识理论知识以后，可以设计难度较大的项目，引导中职生对核心要素进行领会，进而让教学顺利进行.第二，在中职生并未对基础知识进行扎实掌握的情况之下运用项目引导法，完全让中职生进行独立设计以及实施并不合适.此时，教师先对任务驱动方法加以运用，让中职生对新知识以及新技能进行掌握，并储备一定知识，按照循序渐进原则，在之后的教学当中对项目引导法加以运用，使中职生可以快速适应，进而取得应有的教学效果.

二、中职数学教学中项目引导和任务驱动教学法的运用

在项目引导这个阶段，教师对项目问题加以设计，对项目成果进行展示，让中职生看到相应成果，借此激发中职生的实践兴趣.在中职生学习兴趣被激发以后，在教学实践以前，教师需对课程目标加以明确.例如，开展“三角函数”教学期间，主要把现实生活和电学当中三角函数的应用当作项目.

第一，情境引入.教学期间，数学教师可以用一个学时带领中职生到实训基地以及企业进行参观.参观过程当中，教师需启发中职生思考看到的一些现象当中包含什么数学知识，并为中职生准备相应的讨论题，让中职生进行自由讨论.在此之后，数学教师可展示事前准备的例子，顺势引出项目.

通过到实验室当中进行参观以及对沙摆实例进行展示，可以有效激发中职生的学习兴趣，一些学生可以进行自主讨论[1-2].此时，数学教师可以顺势提出问题：假设现在给大家一块半径是0.7米的圆木头，如图1所示，用这块木头做矩形桌面的书桌，请设计一种最佳方案，使书桌面积最大？在实验当中，学生看到在示波器连接家用电源后，屏幕上出现了波形图.此时，教师再次提问：“大家是否可以结合所学知识对这种现象进行诠释呢？”此时，中职生异口同声地说：“因为接通电源产生了电流.”一些中职生在思考：是否只要存在电流，屏幕上就会出现图形呢？此种电流究竟具有什么样的特征？和数学知识存在何种关联？借助此种方式，可以让中职生对所学知识产生深刻印象，有效调动其探究热情以及积极性，促使其学习效率不断提高.

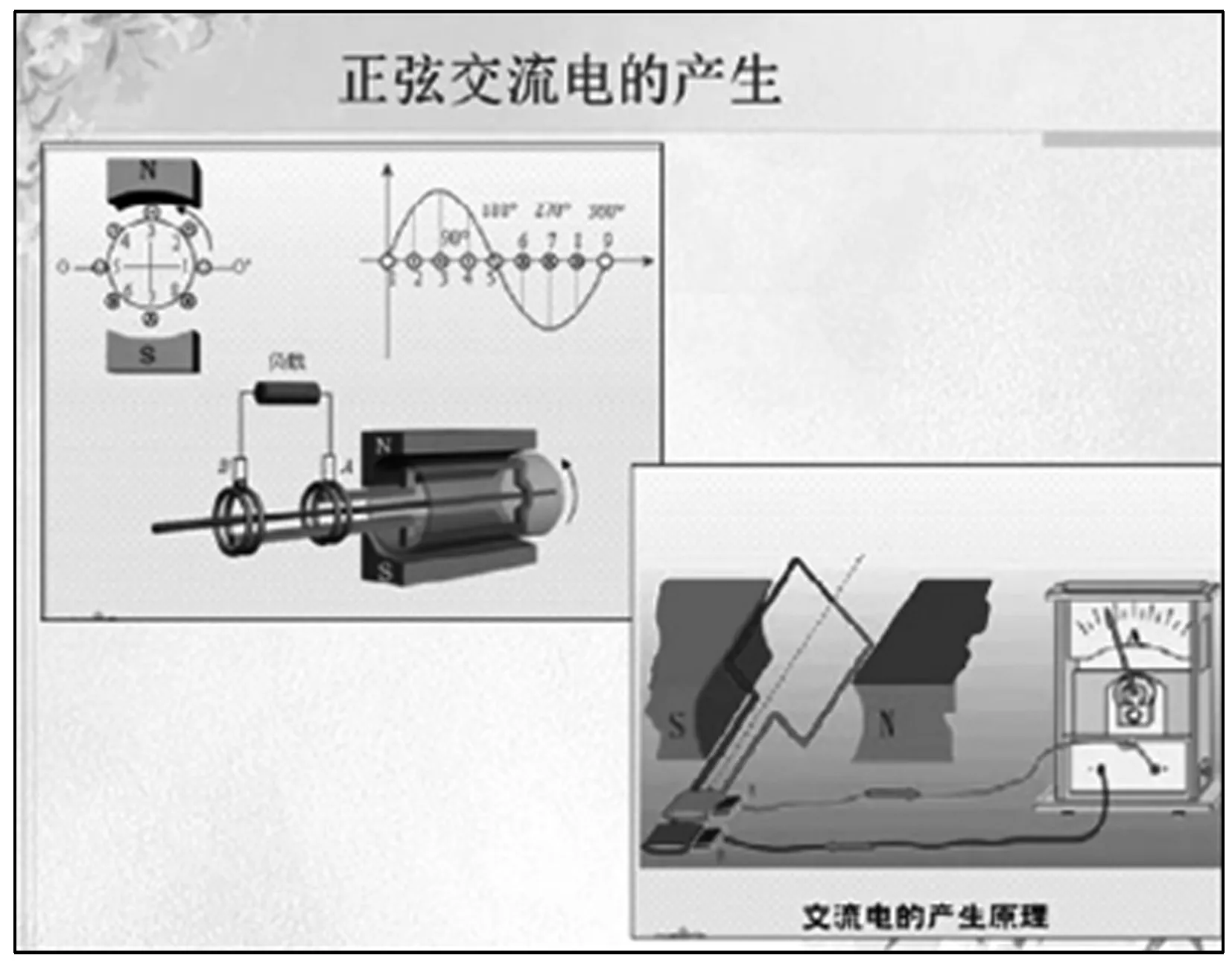
图1

第二，对中职生进行分组，让中职生通过小组形式展开探究.

第三，设计任务，对三角函数实施任务设计，同时对所有子任务对应的任务目标加以确定.

1.任意角和弧度制

在课堂教学中，教师可以通过PPT对任意角旋转过程进行演示，中职生通过对PPT动画进行观察，可以对任意角这个概念进行理解，并可以明确象限角的概念.在此之后，教师可以给中职生布置相应任务，如界限角定义与判断；弧度制定义；弧度和角度的转化公式具体推导.中职生可以先通过小组形式进行讨论，再选派代表进行发言以及总结.

2.任意角的三角函数定义

在教学期间，数学教师可以提出以下问题：回忆锐角的三角函数定义，并对其符号形式进行默写.各个小组可以进行自由讨论.之后，教师可以对任意角的正弦、余弦以及正切函数的定义进行讲解，并对计算器具体用法进行介绍，让一个小组负责计算30°与0°对应的三角函数的值；一个小组计算60°与45°对应的三角函数的值；一个小组计算180°与90°对应三角函数的值；一个小组计算360°与270°对应的三角函数的值；一个小组负责把前面几个小组所得计算结果加以总结并列表.

3.象限角的三角函数值的符号与诱导公式

数学教师可以进行举例，让中职生通过口头形式回答象限角的三角函数的值的符号，让各个小组对判断方法进行讨论，之后选派代表进行发言，对判断方法进行总结.

数学教师可以通过直角坐标系当中的角的表示和三角函数定义，对角-α，180°-α，360°-α，180°+α以及α-180°的余弦、正弦以及正切的诱导公式进行推导，并要求中职生借助计算器对求已知角的三角函数的值的方法进行复习.在此期间，数学教师可以开展分层教学，让基础差的中职生掌握通过计算器进行求值的方法，让基础好的中职生借助诱导公式进行求值.

4.正弦函数与正弦型函数的图象

对于正弦函数，数学教师可以借助PPT动画对一个周期之内的函数图象进行演示.中职生观看以后，可以分组对五点作图法进行讨论.在此之后，各小组可以选派代表进行发言，对讨论结果进行汇总，进而得到正弦函数的性质[3-4].

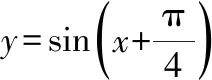
5.电学当中锐角的三角函数和正弦型函数的应用.

教师可以提出以下问题：写出锐角三角函数定义与相应符号；说一说物理以及电学当中锐角三角函数的应用实例.之后，教师可以对有关例题进行讲解.

在任务驱动的理论教学这个阶段当中，教师可进行以下步骤[5-6].

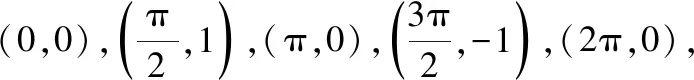
x0π2π3π22πy=sin x010-10

描点画图，进而得到以下图象(如图2)：

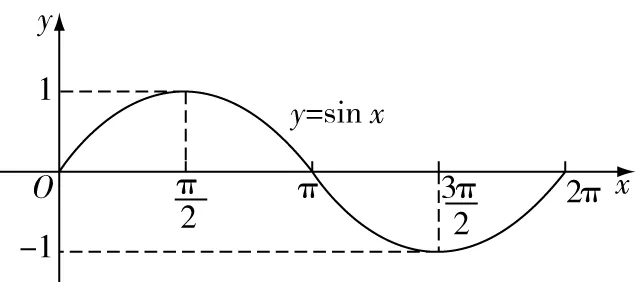
图2

作出一个周期之内的图象后，可以将图象向左右两边延展，这样能够得到整个定义域上标准的正弦函数的图象(如图3)：

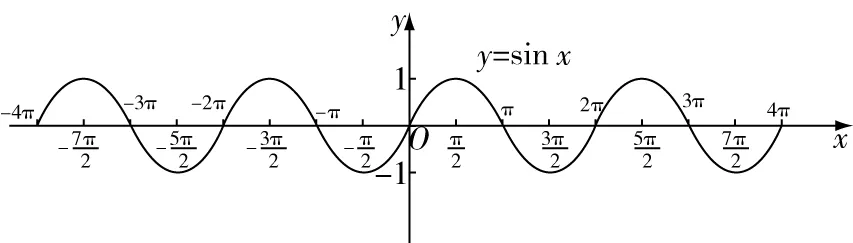
图3

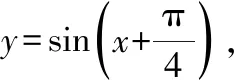
在项目引导这个实践教学的阶段，教师可以采用以下策略.

首先，问题提出与解决方案.

一块半径是0.7米的圆木头，用这块木头做矩形桌面的书桌，请设计一种最佳方案，使书桌面积最大？

通过任务驱动的理论教学，中职生已经对三角函数有关理论知识有了深入了解，但在项目实践当中运用所学知识并非易事，需要通过相应转换以及其他方法对问题进行简单化.如，提出一个类似问题：在一块半径是R的半圆形的钢板之上截取矩形钢板，钢板面积的最大值是多少？中职生可以对此问题进行分析以及讨论.

然后，引导中职生进行分组讨论.

进行问题引导以后，教师可以让中职生进行小组讨论，对问题加以解决.在此期间，教师可以适当参与其中.之所以对上述问题加以设计，是因为中职生并未得到有效锻炼，并未形成较强的知识应用意识，无法对复杂问题进行解决.

最后，在示波器连接家用电源后，屏幕上出现了波形图，引导中职生结合所学知识对这种现象进行诠释.

对问题进行解决以后，项目已经完成了一半.为了让中职生对专业课进行有效学习，教师可以让中职生对上述问题进行探究，这样一来，可以让中职生对专业课程当中数学知识的具体应用进行了解，为其专业课的学习奠定坚实基础.

三、中职数学教学中任务驱动法的有关分析

(一)内涵

任务应突显出针对性和明确性，让学生意识到自己要完成哪些学习任务，突破哪些学习重点，并围绕这些任务与重点来探讨知识，从而取得学习上的进步与成就.据此分析，任务驱动法是以任务来引领学生展开课程知识学习的过程[1].

(二)原则

其一，中职数学课程每章节内容各不相同，而且学生可以探究的内容与问题也很广泛，因此，教师设计的数学学习任务应该多元化，让学生有机会选择适合自己的任务来展开数学课程知识的探索，而不是被动地探究数学课程知识.

其二，教师在应用任务驱动法引导学生开展数学知识探索时，要注意教学时间的合理控制，即给予学生足够多的时间来探讨数学问题，使学生得到良好的课程教学体验.所以，教师要懂得坚持教学的时间合理性分配原则，以满足学生学习与探讨时间为前提，开展数学课程教学工作，使学生得到良好的教学指导[2].

其三，师生互动性是推动数学任务驱动课堂构建的一个重要环节.教师开展任务驱动教学时，要坚持师生互动性原则，鼓励学生多与教师交流，并且，教师也要懂得关爱学生，了解他们的学习难题，并给予他们适当的帮助，只有这样，学生才有动力去完成课程布置的研究任务.

四、中职数学教学中任务驱动法的具体应用

(一)坚持灵活多变的任务来驱动学生的学习

任务驱动教学法在中职数学课堂中应用的目的是提高学生的学习兴趣，因此 ，教师要设计合适的教学任务，进而更好地调动学生的学习积极性.中职数学课堂之中存在学生的学习差异现象，一些学生接受知识的能力比较强，而一些学生则显得比较弱，若教师不懂得因人而异的重要性，则学生将无法得到良好的课程教学.所以，教师对数学任务的设计要灵活多变，以学生想要探讨的数学课程知识、想要理解的数学内容为基础，设计符合学生学习需求的探究任务，让学生在其能力范围之内以及在他们的兴趣爱好之内，展开数学任务探究，从而充分激发学生的数学探究兴趣.另外，教师也要关注到一些学习比较困难的学生，尽可能设计一些简单的任务来驱动该层次学生的学习，让他们从任务探究之中获得成就，从而提升他们的学习信心与动力[3].

(二)以新旧知识任务探讨引发学生的学习兴趣

在教学过程中，教师可以通过提问以前的知识点引入新课，使学生对于新旧知识有更好的衔接.中职生学习能力较弱，因而教师在设计数学学习任务时，应该遵循与时俱进、新旧衔接的教学原则，让学生一步一步地去探究数学知识，而不是一开始就让学生感受到学习的压力.因此，教师需要以学生的数学认知能力为起点，引导他们先以基础的数学概念探讨为起始任务，再到复杂数学任务的探究，使学生探究数学任务的过程平稳，降低数学学习任务的难度.此时，教师需要做好新旧知识的衔接式教学工作，以基础概念到应用问题的探讨，从而鼓励学生多去探讨不一样的数学问题.

以中职数学教学之中的“函数的概念与表示方法”教学内容为例，为了让学生的学习具有一定的任务衔接性，且不让他们感受到学习的压力，教师可以从生活实例探究函数的表示法，引导学生去探讨一些简单的数学学习任务，从而鼓励学生多去探讨相关的数学知识问题.具体地，教师应该先从学生已学的一次函数、反比例函数等内容入手，要求学生回顾已学的函数知识，让他们独立完成已学数学知识复习的任务.然后，教师引入新的数学课程知识内容，即函数的单调性和奇偶性.对于一些函数的实际应用题，教师可以让学生结合函数概念去构建一个新的函数模型，从而鼓励学生探讨函数的概念与表示方法.另外，教师还可以布置一些实践操作环节的数学学习任务，包含计算环节，这有利于锻炼学生的数学运算与探究能力，并且考验学生的探究技能，因而会有很多学生产生学习的兴趣与好奇心，而学生的好奇心会促使他们不断地探究更为深入的数学知识，进而有效发挥出任务驱动式的作用.

结 论

综上可知，在中职院校数学教学当中，对任务驱动加项目引导教学法加以运用，可以充分发挥中职生的主体作用，有效提高中职生的能动性以及学习自信心，促使其形成专业优越感.在实际教学期间，数学教师要对任务驱动加项目引导教学法具有的内涵与应用精髓进行深入探究.只有这样，才能促使教学水平不断提高，进而推动中职院校数学教育持续发展.