基于贝叶斯算法的生产线故障检测方法

2022-01-27王占涛卢新佳张筵凯

桂林电子科技大学学报 2021年5期

王占涛，罗奕，卢新佳，张筵凯

(桂林电子科技大学机电工程学院，广西桂林 541004)

现代智能技术已经渗透到多个领域，形成不同的智能生产方法，设备的操作更加人性化，使现代工业的生产能力得到极大提高，为传统行业实现智能化生产、追上当前智能化工业发展的潮流提供了有利条件。传统的故障检测主要是通过生产现场的巡视人员根据现场的报警信息进行调控，故障发生后，现场巡视人员首先根据报警信息确定报警的生产线，检查各类生产设备及监测装置，确定报警原因及故障点，编写故障事故处理记录，为后续的故障处理提供决策依据[1-2]。这对现场巡视人员的依赖较大，大量工作依靠人工操作来完成，如离线分析、组分检测、手动控制等，生产效率低下，生产成本较高。由于人工操作的时效性不足，导致资源利用率不高，对生产水平的高低有较大影响。科技的快速发展逐渐衍生出的人工智能技术，极大改变了工业生产环境，且在一定范围内得到推广和应用。不同行业的关键技术被迁移、引用到相关或不同领域内，使得工业生产过程的关键技术——故障检测也得到了极大的发展[3]。文献[4]提出了一种以智能控制单元控制的执行机构，结合计量、监测单元，与经典PID控制相比较，该系统具有更小的超调量，响应速率更快等优点。文献[5]提出一种结合极限学习机与D-S证据理论的故障检测模型，通过粒子群优化算法改善学习机模型，形成新的算法，对发动机的故障数据进行学习训练，此方法能够识别发动机的故障类型，诊断效果优良。稀土萃取生产线是一种延伸距离长，故障状态的检测对象数量多、分布广的生产系统。基于智能算法的故障检测方法在复杂装备等故障检测中得到卓有成效的应用，但由于稀土生产自动化水平不高，生产效率较低，该方法在稀土萃取故障检测中的应用还不多见，需要根据稀土萃取工艺设备及流程自身的特点建立相应的智能故障检测方法。

由于AI技术的广泛应用和传感器技术的迅速发展，当工业生产系统失稳时，大量数据的涌现，反而给故障检测的精度和速度带来更大的挑战[6-8]。鉴于此，基于贝叶斯算法理论，提出了一种基于改进贝叶斯算法的故障检测方法。

1 故障检测方法

贝叶斯算法理论总体基于数理统计学，根据具体问题搭建合适的模型，通过对收集到的数据分析研究，确定在实际生产过程中可能出现的故障类型，以便对相应的故障问题做出正确的检测和后续处理。传统的贝叶斯故障检测算法在大数据时代下受到了极大的限制，对于更加复杂的机械系统误判率较高[9]。故障检测方案如图1所示。

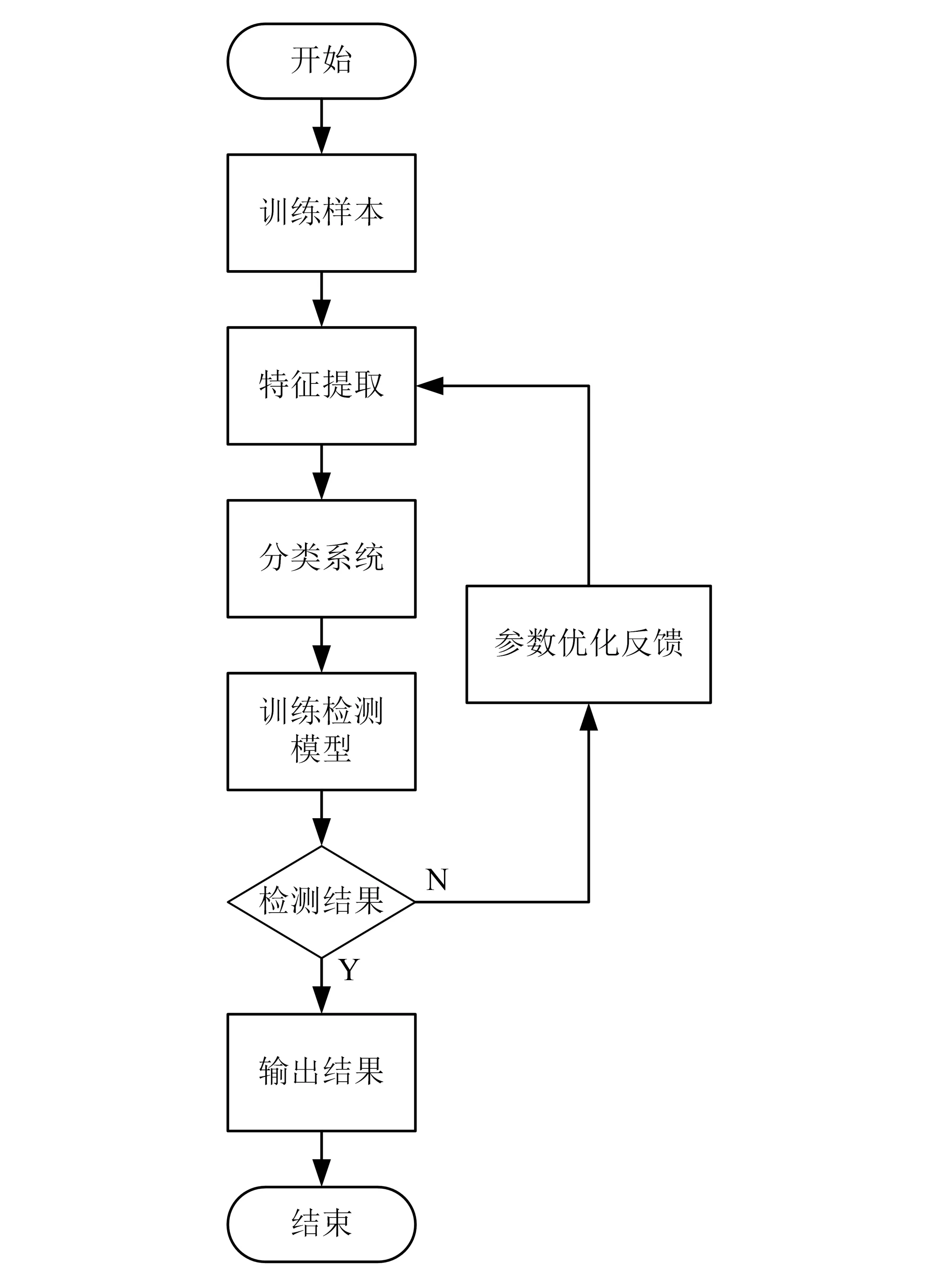
图1 故障检测方案

1.1 贝叶斯算法相关理论

贝叶斯公式[10]是在全概率的前提下得到的，

(1)

其中i=1,2,…,n。

贝叶斯公式最大的优点是可以将所有相关因素动态地联系起来，提高了故障系统判断的准确性。

定义1对某故障类型定义为TF={TF,i|i=1,2,… }。

定义2对某故障类型所对应的特征向量定义为X=(X1,X2,…,Xn)，其中X1,X2,…,Xn为相应的特征分量。

定义3对于出现的特征向量X，发生相应故障TF,i的概率为P(TF,i|X)，根据贝叶斯公式可知：

(2)

其中：P(X|TF,i)为故障TF,i类型发生时对应的特征向量为X的概率；P(TF,i)为故障类型TF,i发生时的概率；P(X)为故障发生时出现对应的特征向量X的概率。

假设特征分量之间相互独立，那么根据统计学中相互独立事件定义，可得

(3)

(4)

其中：Xj为X的第j个特征分量；P(Xj|TF,i)为表示故障类型TF,i时特征分量Xj发生的概率。

当某故障发生时，系统会显示对应的异常，检测设备会检测到不同的数据，表现不同的状态，相对应的特征向量会不相同。实际特征向量的选取主要根据故障类型来选择，并且特征向量的选取应尽可能地包含所有的故障类型，相互之间要满足相互独立的假设。

定义4θ(TF,i)=p(TF,i)/p(TF,i)为TF,i先验概率。先验概率可用下式计算：

(5)

其中D为训练数据集合。

定义5相对于特征分量和故障类型，其似然比定义为

(6)

定义6后验概率定义为

(7)

1.2 改进贝叶斯的故障检测算法模型

对于贝叶斯算法，最主要的问题就是分布函数的确定及先验概率的选取[11-13]。在实际生产过程中，将故障数据分布假设为正态分布，选取样本的频数作为先验概率。ng为用于建立判别函数的已知分类数据中来自第g总体样本数。具体的二次判别分类问题可描述为：存在数据X，其中有m个样本x1,x2,…,xm，每个样本p个属性，类别数为g，函数fg(xm)可以将待测样本x归类为g个类别之一，而它所依据的分类规则由较高的概率决定。数学模型定义为

(8)

其中，Ag、ug分别为类别g的协方差矩阵和均值向量，其样本数表示为ng，由于数据的计算十分复杂，可认为协方差相等，即

A1=A2=…=Ag=A。

(9)

在计算后验概率时，需要建立一个判别式y(g|x)。定义后验概率的计算式为

(10)

其中y(g|x)定义为

y(g|x)=ln(qgfg(x))-Δx，

(11)

Δx是与g无关的部分。由式(11)可知，存在h，使得y为最大，那么P(g|x)必然也最大，即若y(g|x)=maxy(g|x)，则把样本x归入第h类中，对于二分类问题，类别总数g为2。

正则化方法的提出是为了解决贝叶斯的二次判别方法的协方差矩阵的奇异性问题。通过交叉验证将参数λ、γ训练为使分类误差最小化的参数，其定义为

(12)

Si=ni∑i，

(13)

(14)

其中：ni为第i类故障样本的训练个数，n为故障数据的样本总数；k为故障类别总数。

对于分类问题，需将以下目标函数最小化：

w*=argmin∑L(yi,f(xi,w))+λΩ(w)。

(15)

已知多元正态分布总体的贝叶斯判别法，利用K-L散度理论，将其重新定义为

DKL(p1|p2)=E(logp1-logp2)=

(16)

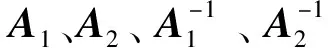
2 实验仿真与分析

2.1 实验仿真

目前，稀土加工生产行业仍然属于劳动密集型产业，生产效率不高，自动化水平较低，对人力依赖性较大[14-16]。萃取生产工序主要将各种不同稀土元素与有机溶剂充分溶解，萃取装置主要包括电动机、搅拌轴、皮带及搅拌罐体。根据在某稀土萃取生产车间故障监测设备得到的数据进行分析，故障主要集中于皮带和电动机这两部分。电力作为驱动装置，是保证系统平稳工作的根本因素，电压是否正常决定了稀土萃取生产设备是否能够正常运行。当供电电压达不到额定电压时，会导致电动机转速发生变化，从而影响皮带的传动效率及转速，进而导致搅拌设备发生故障，影响萃取效果[17-18]。而皮带作为电动机与加工设备之间桥梁，是稀土萃取生产设备能够顺利工作的决定因素。采用的三相异步电动机的额定功率为3 kW，额定电压为380 V，额定电流为6 A，额定转速为200 r/min。根据监测设备采集到的电压数据，结合电气原理，将电信号转换为转速信号。对转速及电压的数据进行信息融合，将融合数据随时间的变化建模为预测变量的函数，分析基于贝叶斯理论与加入K-L散度后的贝叶斯算法间的区别，得到的拟合曲线如图2所示。

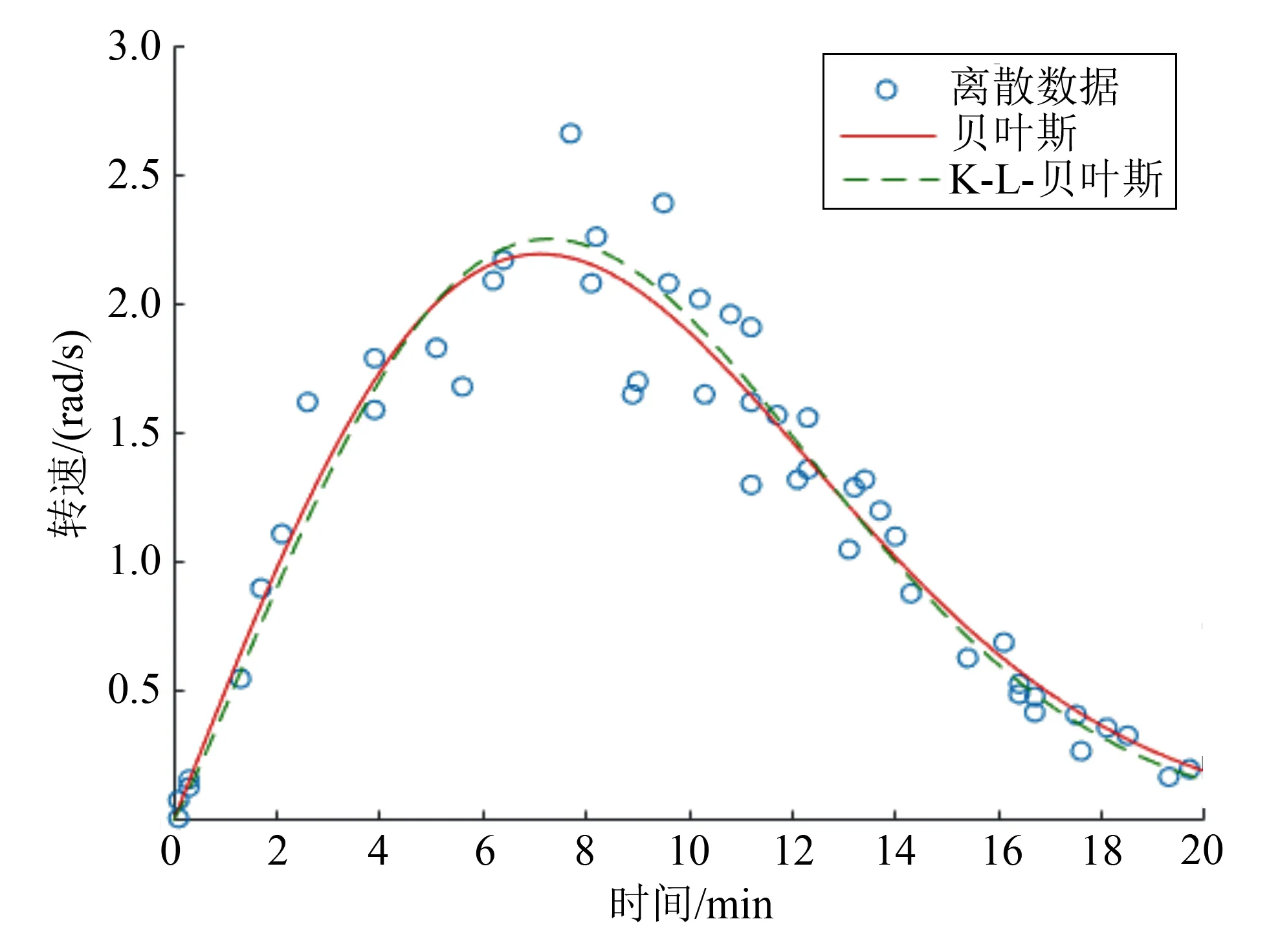
图2 拟合曲线

为了更直观地显示基于贝叶斯理论的故障分类，将从生产线生产运作系统采集到的故障数据进行可视化。数据可视化图如图3所示。

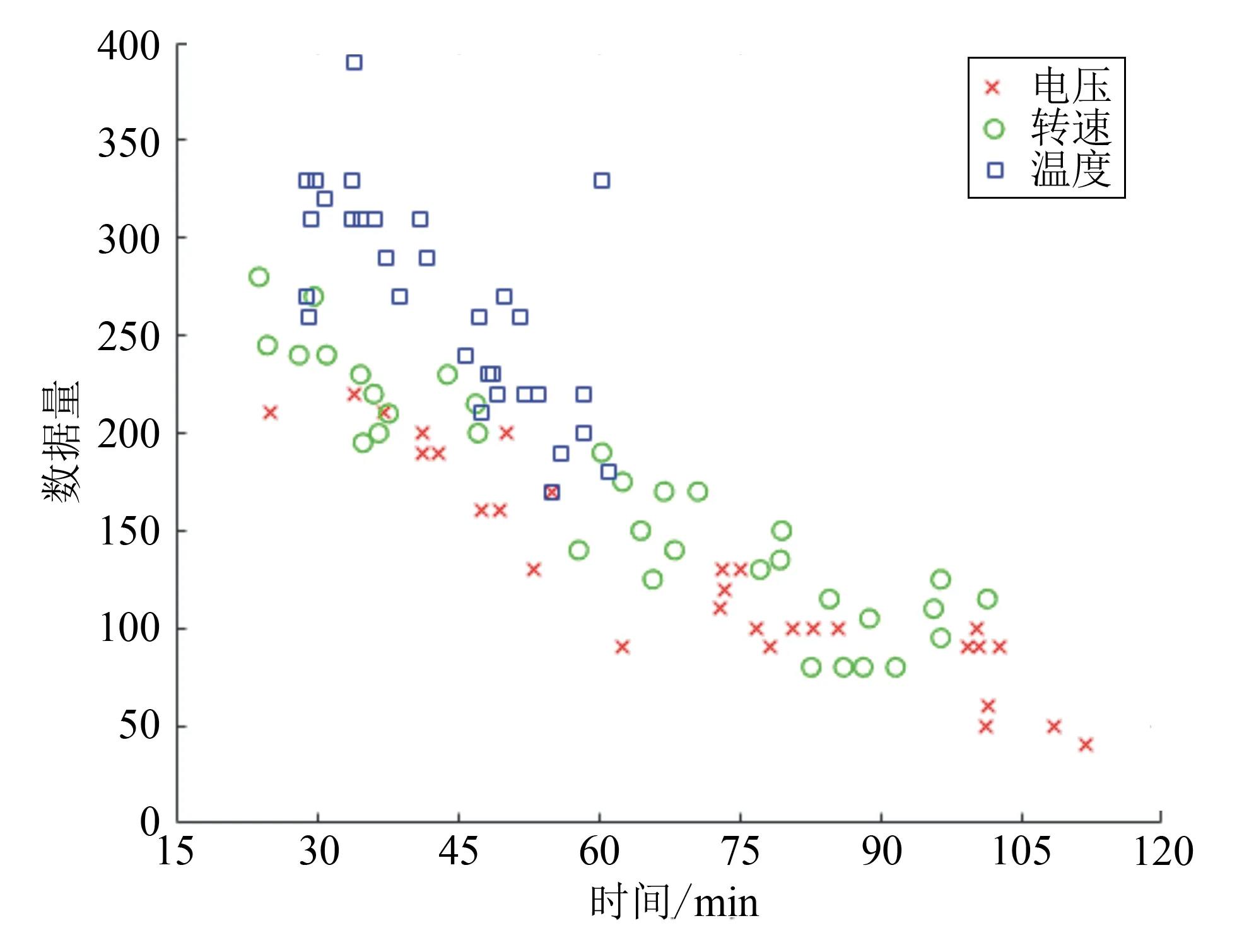
图3 数据可视化图

在进行仿真实验时，可能有一些表示各种故障数据的随机输入。由于相同的随机条件可对2个故障来源都产生影响，若忽略仿真数据的相关性，可能会导致错误的结论。为了尽可能地模拟稀土生产的情况，需要考虑两两输入之间的相关性对仿真结果的影响。因此，在进行算法仿真前，需要有条件地进行数据采集，本研究采取的策略是尝试不同的可能性，以确定模型的相关性。

图4表示故障数据与故障类型之间的线性关系强度(数据在散点图中沿着最小二乘直线排列的松紧度)。对于不同搅拌装置，选用不同长度的皮带相连接，生产过程中所选用的电压等级也不同。从图4(a)可看出，电动机与皮带数据分布相对分散，关联性不强，说明数据可能造成误判；从图4(b)可看出，数据集中程度较大，说明电动机与皮带数据关联性较好，在数学原理上，也体现了电动机和皮带相关数据一一对应的关系，能够形成数据空间，为下一步故障判别提供依据，这种相关性由基础二元正态分布的参数决定。将具有相关性的样本数据进一步进行二次判别。

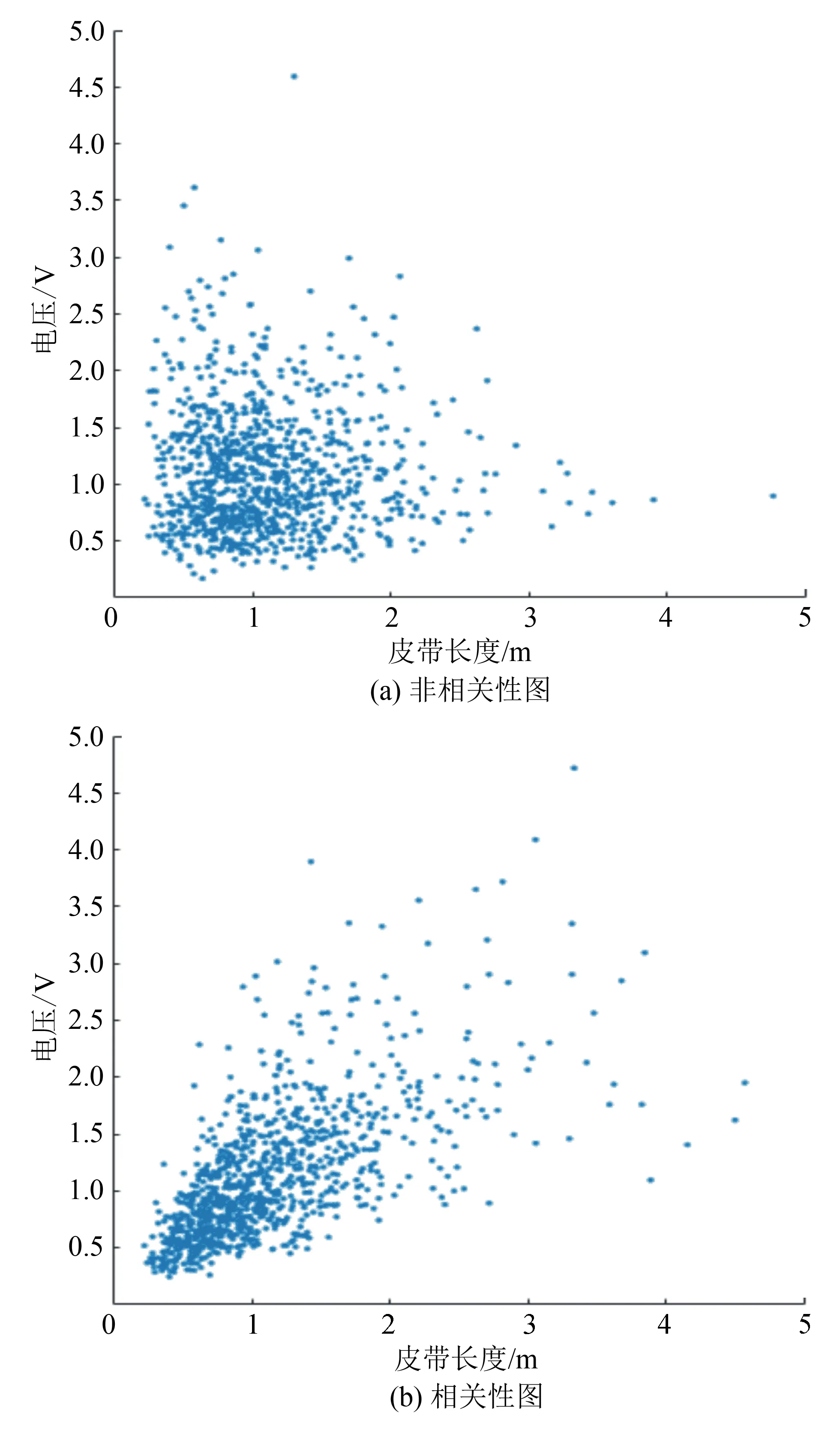
图4 故障因素非相关性、相关性图

皮带与电动机相关参数的变化决定了采样数据的变化，因此也从理论上证明了故障的产生是由皮带和电动机相关参数的变化造成的。为方便表示，在实验中，将故障分为皮带故障、电动机故障。

2.2 改进的贝叶斯判别法

在参数学习和约束条件之间进行迭代，逐渐将公平约束添加到优化中，利用top-k模式判别器进行约束。在每次迭代中，学习受公平性约束的最大似然参数，并使用更新的参数在下一次迭代中将k个模式添加到约束集合。重复该过程，直到搜索算法不再找到判别模式为止。

通过检查模式分类器在搜索期间访问的所有可能模式的歧视分数来表示误判概率，分数越小，歧视程度越低，误判率越低。表1为数据统计分数，使用了判别和发散两级启发式及0.01、0.05和0.1三个阈值。

表1 数据统计分数

通过对数据不断的处理，剔除相关性较小的数据，获得更加准确的贝叶斯判断模型。表2为该模型δ=0.1时剩余的识别模式数量，其中λ决定了数据修复步骤中公平性和准确性之间的权衡。从表2可看出，只要在客观上保持一定程度的准确性，该方法就能有效地进行故障检测。

表2 剩余数据统计判断

通过采集的故障数据，根据经验，首先定义错误类别，f1表示皮带出现故障的分数，f2表示电动机出现故障的分数，分数越相近，表明故障检测结果越准确。采集10组故障信号，利用改进的贝叶斯故障检测模型对其进行故障分类，结果如表3所示。

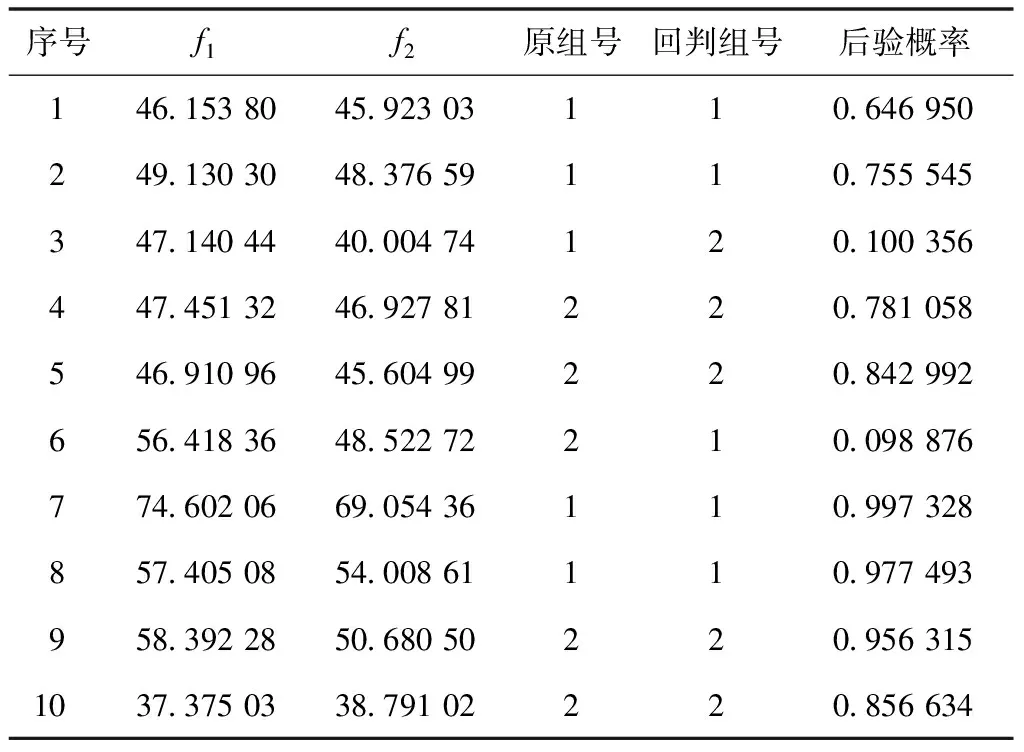
表3 贝叶斯二次判别检测结果

从表3可看出，除了第3组和第6组数据，其它组数据都能正确判定。第3组和第6组数据的后验概率分别为0.100 356、0.098 876，后验概率较小，所以造成误判。通过对相应的原始数据及故障分数进行分析，可能是属于原分组时的错分样品，即单纯使用数据将其分类成2种错误类别，很容易发生误判的情况，因此，要尽量避免使用单纯的数据。