基于互差中值加权的北斗周跳探测算法
2022-01-27曾武陵蔡成林沈文波
曾武陵,蔡成林,2,沈文波
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.湘潭大学 自动化与电子信息学院,湖南 湘潭 411105)
高精度北斗定位普遍采用载波相位值作为定位的原始数据。周跳是定位算法中关键的一部分,未及时处理会出现偏差为米级的较大误差,这引起了国内外相关学者的广泛关注。在单频探测法中,多项式拟合法、多普勒积分法等方法使用较多,但这些方法有其自身的不足之处[1]。双频探测法主要有MW(Melbourn-Wübbena)法、电离层残差法、差分法等。在三频动态相对定位中,一般采用几种方法联合进行定位,如联合MW和无几何方程进行周跳的探测,去除单一方法的局限性[2-6]。有学者利用粗差的模型对周跳进行探测,陈源军[7]提出了基于站际二次差模型的粗差方法探测周跳;李昕[8]提出一种根据单位权中误差估值进行整体检验判断是否存在粗差的方法;单弘煜等[9]提出一种利用历元间差分量进行粗差探测的新方法。在Baarda数据探测法中利用传统加权算法探测精度不高,针对传统加权算法中周跳探测方法的不足,提出了一种基于互差中值加权的北斗周跳探测算法。
1 历元差分模型
假设在某一历元时刻,基准站、流动站共同观测到有效卫星i,经过线性化后的载波相位单站单差观测方程为
λΦt,i=ρt+lt,iVx+mt,iVy+nt,iVz+
c(δt-δt,i)-It+Tt+λNt,i+εt,
(1)
其中:t为历元时刻;i为定位卫星;Φ为原始载波相位值;λ为对应频率的波长;ρ为基站的近似坐标与卫星星历计算的卫星位置之间的站星距;I、T分别为电离层、对流层延迟等空间相关误差;δi为定位卫星钟差;δ为基站接收机钟差;N为未固定的整周模糊度;εt为载波相位观测噪声、多路径效应等误差,该误差项相对于载波相位观测值是一个极小的量,可忽略不计;Vx、Vy、Vz分别为近似点与接收机的基线向量差;lu,t、mu,t、nu,t分别为t历元时刻的坐标分量,
(2)
(xu,t,yu,t,zu,t)、(xu,yu,zu)分别为该历元时刻基准站的卫星坐标和近似坐标。根据方程(1),t+1个历元测站坐标用第t个历元计算坐标为近似点坐标,
λΦt+1,i=ρt+1,i+lt+1,iVx+mt+1,iVy+nt+1,iVz+
c(δt+1-δt+1,i)-It+1,i+Tt+1,i+λNt+1,i+εt+1。
(3)
在历元间进行差分,即差分观测方程为式(3)减式(1),
Vt+1,t=lt+1,iVx+mt+1,iVy+nt+1,iVz+
CΔδt+1,t-Bt+1,t。
(4)
其中:
(5)
在高采样率的情况下,假定历元间的整周模糊度、空间性较强的电离层延迟、对流层延迟等误差相等[10]。误差方程(4)中,站星距可以直接计算,载波相位值可直接从接收机得到,卫星钟差可用拉格朗日插值法内插,只有位置参数和接收机钟差值是未知数,只要在同一历元有4颗以上的有效卫星,可用最小二乘法计算这些未知参数。当第t和t+1个历元间发生周跳,相当于式(4)的Φt+1-Φt出现了粗差,可以用间接平差法进行粗差的探测。
2 周跳探测模型
2.1 互差加权模型
在获取载波相位观测值中,由于接收环境的影响,周跳成为一种不可避免的观测误差。在本模型中,以差分残差值构造数组V=[v1v2vn],设Vmid为残差数组的中位值,将数组V中的每一个元素与Vmid作差,得到一个新的数组Vdif=[vdif,1vdif,2vdif,n]。在差分中,数组V中Vmid与同值作差产生一个零值,取零值Vdif,mid=0.01,这个数值是一个经验证后的较优权值[11]。根据数组Vdif,设粗差探测权矩阵为
(6)
2.2 粗差探测模型
在粗差探测中,Baarda数据探测法有着极其重要的地位。该方法根据构造的残差量对粗差进行探测,可辅助进行周跳的探测。GPS测量数据的统计量服从正态分布[12],根据统计特性,BDS测量数据也可根据卡方分布检验对周跳进行探测。将式(4)的误差方程表达为间接平差模式,
(7)
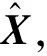
(8)
判断数据中是否含有粗差的假设条件为
(9)
若H1成立,说明参与解算的历元与下一历元的差分解中有粗差,非差载波相位观测值存在周跳。
2.3 粗差观测的定位
当历元数据含有粗差时,需要判断出现粗差的载波相位观测值,即卫星号。在粗差探测模型中,检验单个载波相位观测值是否存在粗差的统计量为标准残差,
(10)

(11)

3 算法验证与分析

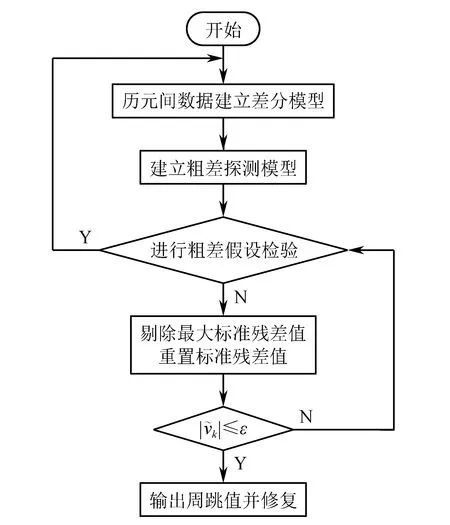
图1 算法流程图
用已提出的三频无几何相位法对一段原始数据进行周跳的探测与修复,确保所用数据无周跳。选取1997~1998历元的数据,传统方差加权和互差加权算法的搜索结果如表1、2所示。从表1、2可看出,数据有效时,这2种算法效果相当,当原始数据中未出现粗差时,标准残差都在阈值以内。
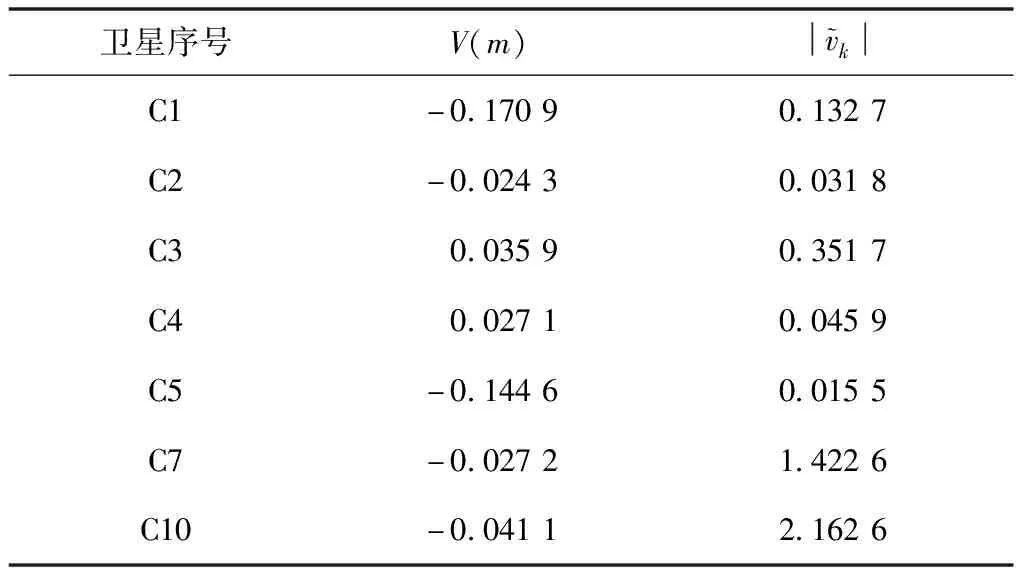
表1 传统加权算法搜索结果

表2 互差加权算法搜索结果
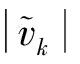
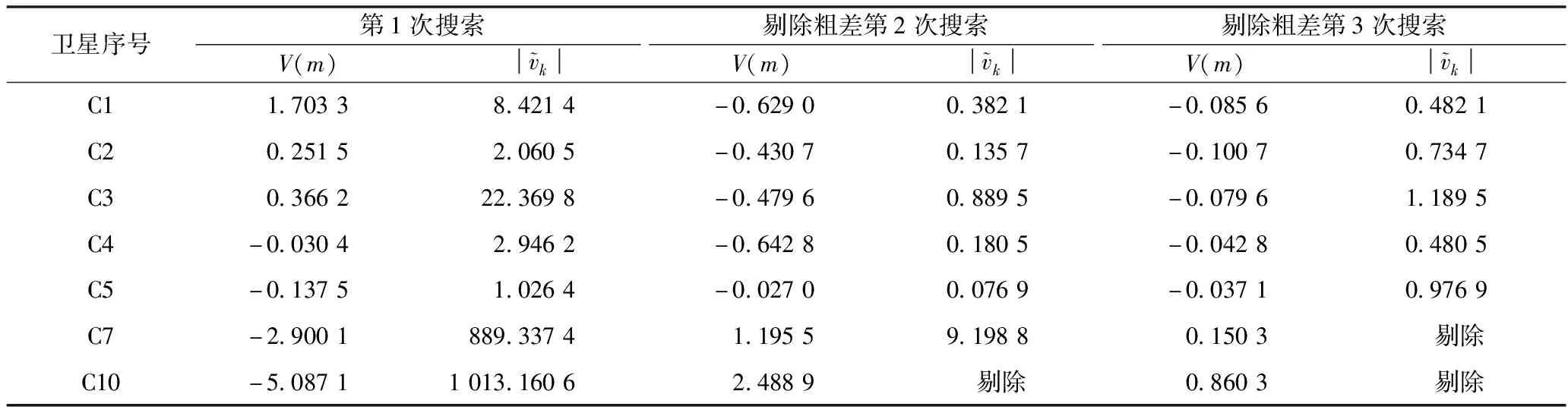
表3 模拟周跳方差加权算法搜索结果

表4 模拟周跳互差加权算法搜索结果
4 结束语
针对方差加权的Baarda探测法探测周跳的不足,基于互差加权算法的Baarda数据探测法,提出以历元间载波相位差分值作为残差构造量的互差中值加权的周跳探测算法,载波相位差分观测值极大地削弱了空间相关性较强的影响,能大大提高定位精度。当载波相位观测值是有效数据时,残差仅受接收机噪声的影响,故残差构造的统计量对周跳十分敏感,本算法适用于动、静态定位。实验结果表明,本算法可探测发生周跳的卫星,其探测精度为1周。与传统加权算法对比,互差加权算法精度有了明显的提升。本算法的不足之处是在实际应用中,当定位卫星小于4颗时,无法计算当前历元的未知坐标参数和接收机钟差,算法会失效。
