轴伸贯流泵压力脉动特性及其改善方法
2022-01-27刘志强张玉全戴庆云郑源吴东磊韦雯倩
刘志强,张玉全*,戴庆云,郑源,吴东磊,韦雯倩
(1.河海大学能源与电气学院,江苏 南京 210098; 2.江苏省秦淮河水利工程管理处,江苏 南京 210098)
贯流泵流道形式简单,水力损失小,效率高,在低扬程泵站中被广泛应用,对于城市供水、排涝防洪、农业灌溉等领域具有重要作用[1-2].泵的运行稳定性一直是研究重点,泵内流场压力脉动及流动旋涡等是影响水泵稳定运行的重要因素.
国内外学者对泵内流场压力脉动特性及其复杂流态演化做了大量研究.周强等[3]验证了模态节径模式分析方法预测泵内压力脉动分布的可行性,表明离心泵导叶流道进口处压力脉动主要受叶片通过频率及其倍频影响.张宁等[4]研究发现口环间隙对于泵内压力脉动能量的影响呈先减后增的非线性关系,合理的口环间隙能有效降低泵内压力脉动水平.郑源等[5]研究了轴流泵在失速工况下泵内低频压力脉动的产生机理,发现导叶体内漩涡的发展演化频率与低频脉动频率接近,表明低频脉动诱导源为导叶体内的漩涡.李伟等[6]对混流泵压力脉动进行测量,表明叶轮出口与导叶进口之间受动静干涉影响明显,压力脉动主频随流量减小向高频偏移,叶轮中部监测点压力脉动受流量影响最大,而远离叶轮监测点压力脉动受流量变化影响减小.冯卫民等[7]研究表明,小流量工况下后置导叶内涡旋为导叶出口低频脉动出现的原因,前置导叶正角度调节可改善小流量工况下泵内流态,大流量工况下前置导叶负角度调节则能降低低频脉动幅值并提高泵效率.
以往对泵的压力脉动特性研究主要集中在离心泵、混流泵及轴流泵等方面,而对于贯流泵的研究较少.同时水泵的优化设计对于节能降耗意义重大,使用导流板优化改善贯流泵的压力脉动特性及流道内流态有助于提高泵的效率和运行稳定性.文中基于CFD数值模拟并结合真机试验,以某泵站轴伸贯流泵为研究对象,采用在其出水流道内增设导流板的方案,探究导流板对轴伸贯流泵在不同工况下的压力脉动特性及流道内流态影响,从而为水泵优化设计及提高运行稳定性提供一定参考.
1 数值计算
1.1 计算模型及网格划分
图1为轴伸贯流泵计算模型,该模型过流部件包括进水流道、前导叶区、叶轮室、后导叶区及出水流道共5部分,其主要设计性能参数及几何参数分别为扬程Hd=2.5 m,流量Qd=10 m3/s,转速n=250 r/min,叶轮直径D=1.7 m,叶轮叶片数为4,前置导叶叶片数为5,后置导叶叶片数为7.
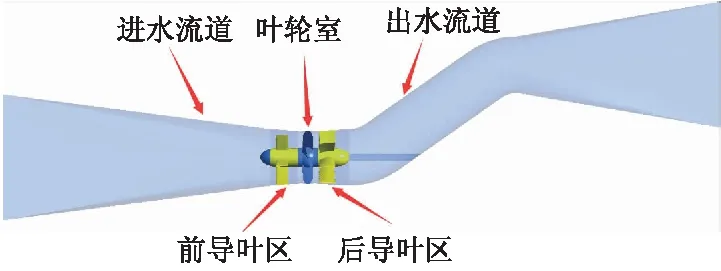
图1 计算模型
为改善轴伸贯流泵压力脉动特性及其出水流道的旋涡流态,采用在出水流道弯管段内放置导流板的方式进行优化设计.导流板由1个中空的圆筒以及与中空圆筒圆周面相切的3块平板组成.出水流道弯管段直径Dc=1 800 mm,导流板轴向长度L=1 200 mm,导流板放置位置如图2a所示,图2b为导流板轴向中心处的特征截面A-A尺寸,其中导流板圆筒外半径为300 mm,内半径为275 mm,平板厚度为20 mm.

图2 导流板
应用ICEM CFD软件采用自适应性较好的非结构化网格对计算模型进行划分.对近壁面区采用边界层网格,并在近壁面区加密网格,以更好地捕捉近壁面区的流动.进行网格无关性检验,共采用6种不同网格数方案,当原模型网格总数大于340万时,其扬程波动小于1%,故最终确定原计算模型网格总数为340万.优化模型的网格总数为475万,其中进水流道292 826,前导叶区1 043 679,叶轮室1 825 244,后导叶区754 250,出水流道834 816,网格质量均在0.3以上.
对原模型及优化模型在额定工况下分别进行定常数值计算,结果如表1所示.可以看出,导流板的增设使得流道过流断面面积减小,水头损失增大,从而泵的扬程及效率均有所降低.

表1 优化前后泵扬程和效率对比Tab.1 Comparison of head and efficiency before and after optimization
1.2 流场数值计算
应用Fluent软件进行数值模拟[8-9],其中湍流模型选取RNGk-ε模型,边界条件设为质量流量进口和自由出流出口,交界面为“Interface”,壁面为无滑移光滑壁面类型.叶轮转动周期为0.240 s,非定常计算时间步长设为0.005 s,即叶轮每转过7.5°的时间,计算时长为2.4 s,即10个转动周期.
为获得泵内部流场的压力脉动信息,在前导叶进口、叶轮进口、叶轮出口及后导叶出口等各截面设置监测点,如图3所示.各截面上监测点均沿半径均匀设置2组,前导叶进口处监测点为a1—a4,叶轮进口监测点为b1—b4,叶轮出口监测点为c1—c4,后导叶出口监测点为d1—d4.

图3 监测点设置
2 结果分析
2.1 真机试验验证
试验在江苏南京秦淮新河泵站进行,在5号机组前置导叶前端与叶轮前端部位开孔进行压力脉动测试,测试过程中保证压力传感器与管道垂直安放.压力传感器选用昆山御宾电子科技有限公司的HPT900高频动态压力传感器,其精度为0.5%.
真机测试在转速为250 r/min下进行,选取压力脉动测试的采样频率为1 000 Hz,则采样时间间隔为0.001 s.真机试验测量过程中,调试好仪器后,先测量30 s机组未运行状态,开启机组,直接记录从开机到停机全过程的压力脉动.
额定工况下非定常数值计算10个周期,取稳定运行的3.8~5.0 s真机试验数据与原模型额定工况下数值计算后5个周期监测点数据进行对比,结果如图4所示.

图4 数值计算与试验数据对比
由图4可以看出:前导叶前端处数值计算与试验的时域数据波形基本一致,幅值略有偏差,各监测点数据与试验数据相对误差在6%以内;受泵管壁开孔采样点限制,叶轮前端监测点数值计算与试验的时域数据波形稍有偏差,靠近轮缘处2点的幅值与试验数据有较大偏差,靠近轮毂处的监测点b1幅值与试验数据较吻合,相对误差为7%;在前导叶前端处试验数据与监测点数据压力脉动主频均为转频4.17 Hz,叶轮前端处二者的压力脉动频域信号主频、次频一致,主频为叶频16.67 Hz,次频为转频4.17 Hz,表明文中所采用的数值计算模型能够较为准确地预测轴伸贯流泵内部流场流动特性,这为进一步分析压力脉动及出水流道内流态提供了保证.
2.2 压力脉动特性对比分析
2.2.1 压力脉动时域特性
文中泵装置模型数值计算均为泵正向运行工况,所对应真机运行流量不小于0.6Qd的工况点皆位于其正向运行水力性能曲线驼峰右侧,高于失速点,故选取0.6Qd及1.0Qd工况进行研究.为描述各监测点的压力脉动特性,定义量纲一化压力系数Cp为
(1)
式中:pi为监测点在某一时刻的静压值;pave为1个转动周期内静压的平均值.
数值计算采取10个转动周期的压力脉动数据,限于篇幅,仅选取原模型及优化模型的监测点a1,b1,c1,d1处的数据进行分析.图5分别为0.6Qd工况及1.0Qd工况下各监测点处原模型与优化模型压力脉动变化时域图.

图5 不同流量工况下各监测点压力脉动时域图
由图5a可以看出:在0.6Qd工况下,在前导进口监测点a1处,原模型与优化模型压力脉动幅值变化均较大,原模型的压力脉动幅值变化小于优化模型;在叶轮进口监测点b1处,原模型与优化模型压力脉动变化周期性规律较好,在叶轮1个旋转周期内有4个明显的波峰和波谷,与叶轮叶片数相同;在叶轮出口监测点c1及后导叶出口监测点d1处,原模型压力脉动幅值变化剧烈,优化模型的压力脉动幅值变化远远小于原模型.
由图5b可以看出:在1.0Qd工况下,原模型与优化模型的监测点压力脉动周期性规律较强,在前导叶进口监测点a1处,原模型与优化模型监测点压力脉动呈周期性变化,原模型压力脉动信号波峰与波谷之间存在一定的随机脉动信号,波形出现二次波峰,优化模型压力脉动在1个叶轮旋转周期内存在5个明显的波峰与波谷,与前导叶叶片数相同,并且脉动变化幅值要远远小于原模型,说明在该工况下优化模型的前导叶片导流作用更明显;在叶轮进口监测点b1处,原模型与优化模型的压力脉动在1个叶轮旋转周期内存在4个明显的波峰与波谷,与叶轮叶片数相同,且优化模型的压力脉动变化幅值大大减小;在叶轮出口监测点c1处,原模型与优化模型的压力脉动周期性变化规律明显,脉动变化幅值相似,但在1个叶轮旋转周期内压力脉动变化剧烈,存在一定随机脉动信号,波形出现二次波峰,该处受动静干涉影响强烈;在后导叶出口监测点d1处,原模型压力脉动变化不规则,优化模型压力脉动呈一定周期性变化,但脉动幅值变化较原模型要大.
比较图5a和图5b,在额定流量工况下,原模型与优化模型的压力脉动时域特性均优于小流量工况,但不同流量工况下叶轮进口处压力脉动周期性均较明显.出水流道导流板在小流量工况下对叶轮后2个截面处压力脉动改善效果明显,额定流量工况下有效降低了叶轮前2个截面处的压力脉动幅值.
2.2.2 压力脉动频域特性
图6分别为0.6Qd工况及1.0Qd工况下各监测点处原模型与优化模型压力脉动变化频域图.

图6 不同流量工况下各监测点压力脉动频域图
由图6a可以看出:在0.6Qd工况下,原模型与优化模型在监测点a1,b1,c1及d1处的压力脉动信号低频区成分较复杂,在前导叶进口a1处,原模型与优化模型压力脉动在0~35 Hz之间存在不同程度次频,原模型压力脉动的主频为13.33 Hz,次频在转频4.17 Hz处最明显,优化模型压力脉动主频为3.33 Hz,次频成分较原模型复杂;在叶轮进口监测点b1处原模型与优化模型压力脉动主频均为叶频16.67 Hz,在0~35 Hz之间存在不同程度次频,但频率信号幅值较小;在叶轮出口监测点c1及后导叶出口监测点d1处,原模型压力脉动主频均为转频,在0~35 Hz之间存在复杂的次频成分,其中监测点c1处次频在叶频处最明显,但在监测点c1和d1处优化模型的压力脉动信号幅值均大幅下降,且主频与次频差别不大.
由图6b可以看出:在1.0Qd工况下,原模型前导进口监测点a1处主频为转频,并存在频率为叶频、前导叶通过频率的次频,叶轮进口监测点b1处主频为叶频,存在频率为转频、2倍叶频的次频;优化模型前导进口监测点a1和叶轮进口监测点b1处的压力脉动频率成分较原模型单一,次频影响不显著,监测点a1处主频由转频变为前导叶通过频率,监测点b1处主频依旧为叶频;叶轮出口监测点c1及后导叶出口监测点d1处优化模型压力脉动次频成分较原模型增多,其中监测点c1处主频由转频变为2倍叶频,但次频影响非常大,存在多处不同程度的次频,监测点d1处主频由转频变为5倍转频,并存在为转频频率的次频.
比较图6a和图6b,在小流量工况下,原模型与优化模型的压力脉动频域特性较额定工况要差,增设导流板后,小流量工况下叶轮后2个截面处的压力脉动低频成分得到改善,额定流量工况下导流板有效改善了前导进口及叶轮进口处的低频脉动成分.
2.3 出水流道涡带
为研究导流板对出水流道内流态的影响,基于QC准则[10]对小流量工况及额定流量工况下原模型与优化模型的出水流道内涡核分布进行对比,分析导流板对出水流道内的消涡效果.QC准则计算公式为
(2)
式中:Wij为涡量幅值;Sij为应变率幅值.
不同流量工况下原模型与优化模型出水流道内涡核对比如图7所示,对应时刻均为2.4 s,所设阈值均为QC=0.002.
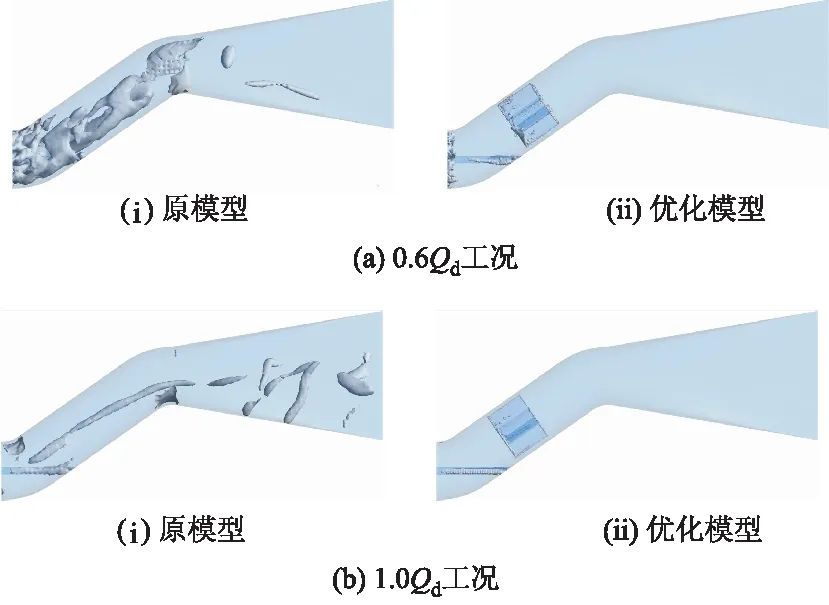
图7 不同流量工况下原模型与优化模型出水流道涡核对比Fig.7 Comparison of vortex core in outlet flow chan-nel between original model and optimized model under different flow rate conditions
由图7a可以看出:在0.6Qd工况下,原模型出水流道内涡带呈直径较大的破碎中空带状,大量存在于弯管段内,由出水流道进口环绕转轴向出水流道扩散段发展,而优化模型出水流道内仅在出水流道进口、流道内转轴及导流板叶片边缘处存在少量涡带,导流板消涡效果十分明显.
由图7b可以看出:在1.0Qd工况下,原模型出水流道内少量涡带环绕转轴,并在其附近发展出一条长涡带,长涡带在扩散段流道内呈螺旋状向出水流道出口发展,相较于0.6Qd工况下其内部涡带更加规则,直径尺寸更小.增设导流板后同样只在转轴及导流板边缘处存在少量涡带,相较于0.6Qd工况下消涡效果更佳.
3 结 论
1) 对轴伸贯流泵模型进行数值计算,所得压力脉动结果与真机试验结果吻合较好,表明文中所采用的数值计算方法能较准确预测轴伸贯流泵内部流场压力脉动特性.
2) 小流量工况下原模型与优化模型的压力脉动时域特性、频域特性较额定工况下差,但不同流量工况下叶轮进口处压力脉动特性均受到旋转叶轮显著影响.额定工况下,增设导流板能有效改善叶轮前泵内的压力脉动特性,降低脉动变化幅值及其低频成分.小流量工况下增设导流板能改善叶轮后泵内的压力脉动变化幅值及其低频成分.
3) 不同流量工况下导流板的消涡效果均十分显著.文中导流板的型式、尺寸及安置位置仅有一种,后续可针对这3个影响因素对轴伸贯流泵的压力脉动特性的影响进行进一步研究,以得出较优方案.
