边界约束条件对箱形梁畸变效应的影响
2022-01-26王妍张元海王晨光
王妍,张元海,王晨光
(兰州交通大学土木工程学院,甘肃兰州,730070)
箱梁截面在畸变时除了产生翘曲应力外,还会发生横向弯曲,进而产生相应的横向弯曲应力[1−3]。随箱形梁壁厚逐渐减小以及波形钢腹板箱梁等组合箱梁的应用,由截面畸变引起的翘曲正应力和横向弯曲应力在箱梁桥总应力中所占的比例逐渐增大[4−7]。
目前应用最为广泛的畸变效应解析方法为BEF Method[8−9],该法选取左腹板与底板夹角在畸变变形中的改变量为基本未知量,利用畸变控制微分方程与弹性地基梁挠曲微分方程之间的比拟关系求解畸变效应,但是这种方法计算过程复杂,且不能与箱梁约束扭转的解析理论相统一。针对此问题,张元海等[10−11]采用箱梁约束扭转的思路,选取畸变中心处的直角在畸变变形中的改变量为基本未知量,建立了畸变效应解析公式。此外,畸变效应解析法还有广义坐标法[12]、板元分析法[13]、纽玛克法[14]等,各种方法计算精度以及对畸变变形未知量的选取和定义有所不同。在此基础上,徐勋等[15−17]研究了剪切变形、截面几何特性、列车运行时速等对箱梁畸变效应的影响,得出畸变变形受剪切变形的影响很小、能综合反映畸变效应的几何特性参数λ、单线活载偏心作用下箱梁跨中截面的翘曲比例系数可达10%左右。目前,有关畸变效应分析的文献都以单一桥型为例揭示畸变效应,其中大多为简支梁[18−19],少数为悬臂梁[20],针对边界约束条件不同的箱梁综合分析畸变效应的文献较少。然而,实际工程中的箱梁很少采用单跨简支体系,悬臂梁也仅是施工过程中存在的一种结构状态,更为常见的是连续体系,包括连续梁与连续刚构。复杂连续体系可看作简单体系的组合,例如连续刚构桥的边跨可近似认为是一端固定另一端简支的受力状态,而中跨就可近似认为是两端固定的力学计算模型。因此,研究边界条件不同的箱形梁桥畸变效应,有助于工程设计人员在设计中更加方便、快捷地考虑畸变效应。
本文采用张元海等[10]所提畸变效应解析思路,推导竖向偏心均布荷载作用下不同边界组合情况下的箱梁畸变效应解析解。通过引入畸变效应边界影响系数,结合数值算例详细分析高宽比、悬臂板相对宽度变化时边界约束条件对箱梁畸变效应的影响。
1 畸变控制微分方程
单室梯形箱梁横截面畸变变形如图1所示,其中,O−xyz为形心坐标系,q为竖向偏心荷载,e为荷载偏心距。D为畸变中心,A和B分别为以D为角点所组成的直角与箱壁的交点,选取直角∠ADB在畸变变形中的改变量为畸变角γD,A′和B′分别为直角∠ADB变形后A和B两点所在位置,则γD=γD1+γD2,图中其他变量为箱形梁截面尺寸。

图1 箱梁畸变变形图Fig.1 Distortion deformation of box girder
用ω表示箱梁截面的畸变扇性坐标,则畸变翘曲正应力σD可通过所选取的基本未知量即畸变角γD表达为

式中:E为弹性模量;ωD为以畸变角γD为基本未知量计算的畸变扇性坐标[10]。
由式(1)可求得畸变翘曲应变能U1为

式中:IωD为箱形梁畸变翘曲惯性矩;l为梁跨径。
图2所示为沿箱梁跨径方向截取的单位长度梁段形成的横向框架变形图,根据转角位移方程可求得图2中所示点1和点2的横向弯矩为

图2 横向框架变形图Fig.2 Deformation of transverse frame

式中:IR1和IR2为箱形梁畸变框架特性参数。
因框架弯矩具有左、右反对称性,故由式(3)可求得框架畸变挠曲应变能U2为

式中:IR为箱形梁畸变框架特性参数。
将箱梁上作用的竖向偏心荷载分解成的竖向反对称荷载记为pD,则外荷载势能V可表达为

畸变总势能Π=U1+U2+V,则

对式(6)进行一阶变分,得
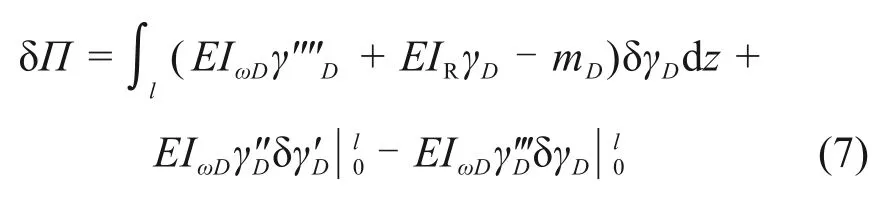
根据最小势能原理,令总势能的一阶变分为0,可得:

式(8)即为畸变控制微分方程,式(9)为边界条件。化简式(8),可得

式中:λ为箱梁畸变特性参数,可综合反映箱梁抵抗畸变变形的能力。
由边界条件式(9)可知,畸变矩MD及畸变双力矩BD的表达式为:

由式(1)和式(12)可得畸变翘曲正应力的一般表达式为

当箱形梁承受均布畸变矩荷载mD时,畸变控制微分方程式(10)的通解为

求解式(14)中4 个积分常数所用到的边界条件为:固定端,γD=γ′D=0;简支端(设置刚性横隔板),γD=γ″D=0;自由端,γ″D=γ‴D=0。
2 不同边界条件下箱形梁畸变效应
本文以SS箱梁、FS箱梁、FF箱梁分别表示简支箱梁、左端固定右端简支箱梁和两端固定箱梁。
图3所示为承受竖向偏心均布荷载q作用的SS箱梁,求解SS箱梁畸变角表达式(14)中的4个积分常数所需的边界条件为:γD(0)=0,γ″D(0)=0;γD(l)=0,γ″D(l)=0。

图3 SS箱梁承受均布荷载Fig.3 SS box girder subjected to uniform load
利用上述4 个边界条件可求得SS 箱梁承受竖向偏心均布荷载q作用时的4 个积分常数C1SS,C2SS,C3SS和C4SS分别为

图4所示为FS箱梁承受竖向偏心均布荷载q作用的示意,求解FS 箱梁畸变角表达式所需的边界条件为:γD(0)=0,γ′D(0)=0;γD(l)=0,γ″D(l)=0。从而可求得FS 箱梁的4 个积分常数C1FS,C2FS,C3FS和C4FS分别为


图4 FS箱梁承受均布荷载Fig.4 FS box girder subjected to uniform load
图5所示为FF箱梁承受竖向偏心均布荷载q作用的示意,其两端边界条件为:γD(0)=0,γ′D(0)=0;γD(l)=0,γ′D(l)=0。从而可求得4 个积分常数C1FF,C2FF,C3FF和C4FF分别为

图5 FF箱梁承受均布荷载Fig.5 FF box girder subjected to uniform load

将式(15)~(17)分别代入式(14),即可得SS箱梁和FS 箱梁、FF 箱梁的畸变角解析解。对式(14)求二、三阶导数后,代入式(11)与式(12)即可得3 种边界约束条件下箱形梁承受竖向偏心均布荷载作用时的畸变矩、畸变双力矩的解析解:

代入相对应的4 个积分常数,直接利用式(3)、式(13)、式(14)、式(18)和式(19)就可计算3 种边界约束条件下箱梁的畸变效应。本文推导的3种边界条件下箱形梁畸变效应解析式只适用于竖向偏心均布荷载作用的情况,对于竖向偏心集中荷载作用下的解析解需另行推导。
3 数值算例
箱形梁横截面尺寸如图6所示,图中所示k1,k2和k3为计算关键点,箱梁承受竖向偏心均布荷载q=20 kN/m,荷载偏心距e=2.35 m,材料弹性模量E=35 GPa,跨度l=40 m。可计算出竖向反对称荷载pD=10 kN/m,均布畸变矩荷载mD=23.5 kN·m/m。

图6 算例横截面尺寸Fig.6 Cross section dimension of sample
为验证本文所推导解析式的正确性,采用有限元软件ANSYS中的SHELL63壳单元建立模型进行数值模拟,将作用在箱梁上的竖向偏心均布荷载分解得到的畸变荷载施加在箱梁各板元对应的单元节点上就能得出畸变效应结果。因有限元软件ANSYS建模输出的结果只能提取应力和横向单宽弯矩,而畸变双力矩、畸变矩、畸变角这些广义内力及位移无法直接获得,故将ANSYS模型计算得到的箱梁跨中截面计算关键点的翘曲正应力及横向单宽弯矩结果与用本文解析式计算的结果分别列于表1和表2进行比较。以SS箱梁跨中截面畸变效应值为基准,引入畸变效应边界影响系数ζ,ζFS和ζFF分别为FS 箱梁或FF 箱梁跨中截面畸变效应值与SS箱梁对应值的比值。
从表1和表2可以看出:按ANSYS 模型计算得到的箱形梁跨中截面计算关键点的结果与用本文解析式计算的结果吻合良好。表1中FF 箱梁的跨中截面畸变翘曲正应力ANSYS值与解析解相对误差较大的原因主要是,在推导解析解的过程中采用了3个假定[7],而ANSYS模型能综合考虑剪切变形、弯扭耦合等因素,且FF 箱梁在两端节点上采用全约束使应力集中更为显著。
表3和表4所示为箱形梁跨中截面的畸变角与畸变双力矩结果。
对比表1和表3、表2和表4可发现:截面畸变角和横向单宽弯矩、畸变双力矩和翘曲正应力的边界影响系数ζFS对应相等,ζFF也对应相等。
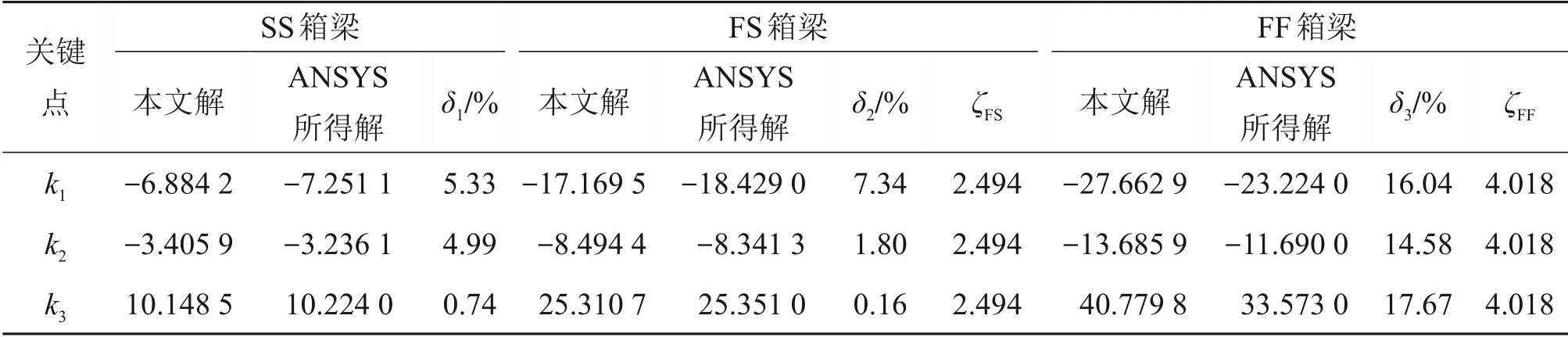
表1 跨中截面畸变翘曲正应力比较Table 1 Comparisons of midspan distortion warping normal stress kPa

表2 跨中截面横向单宽弯矩比较Table 2 Comparisons of midspan transverse unit-width bending moment kN·m/m

表3 跨中截面畸变双力矩比较Table 3 Comparison of midspan distortion bi-moment kN·m2

表4 跨中截面畸变角比较Table 4 Comparison of midspan distortion angle 10−5rad
为了分析边界约束条件对箱形梁畸变效应的影响,保持图6所示截面的尺寸、荷载及偏心距不变,按本文方法计算得出3种边界约束条件下箱形梁畸变效应的纵向分布如图7所示。因计算关键点k2和关键点k3之间存在应力比β[7,10],故选取关键点k1和关键点k3来表征畸变翘曲正应力变化规律。
由图7可以看出:FF 箱梁的畸变效应纵向分布曲线较为陡峭,SS 箱梁的畸变效应纵向分布曲线较为平缓,而FS 箱梁的畸变效应纵向分布曲线始终介于两者之间。由此可知,梁端约束越强,畸变效应纵向分布曲线越陡峭。截面畸变角和横向单宽弯矩、翘曲正应力和畸变双力矩分别具有相同的纵向分布规律,这也印证了表1~4中对应的边界影响系数对应相等的情况,故详细分析畸变角和翘曲正应力的变化规律就可获得横向单宽弯矩和畸变双力矩的变化规律。

图7 箱形梁畸变效应纵向分布Fig.7 Longitudinal distributions of box girder distortion effect
定义高宽比为梁高与箱室宽度之比,求得高宽比变化时箱形梁跨中截面的畸变角、翘曲正应力变化曲线如图8所示。
由图8可以看出:随高宽比增大,箱形梁跨中截面的畸变角先增大后减小,SS 箱梁跨中截面翘曲正应力单调增加,而FS箱梁和FF箱梁的则先增大后减小;当高宽比约为1.06 时,翘曲正应力的边界影响系数相等;当高宽比小于1.06 时,SS 箱梁跨中截面翘曲正应力最小,FF 箱梁跨中截面翘曲正应力最大;当高宽比大于1.06 时则相反,但FS 箱梁跨中截面翘曲正应力始终介于两者之间。高宽比越大,畸变效应的边界影响系数越小,即随高宽比增大,边界约束对畸变效应的影响会减小。
定义悬臂板相对宽度为悬臂板宽度与箱室宽度之比,求得悬臂板相对宽度变化时箱形梁跨中截面的畸变角、翘曲正应力变化曲线如图9所示。
由图9可以看出:随悬臂板相对宽度增大,畸变角的边界影响系数逐渐减小;当悬臂板相对宽度约为0.157时,畸变角的边界影响系数相等;当悬臂板相对宽度小于0.157时,SS箱梁跨中截面畸变角最小,FF 箱梁跨中截面畸变角最大;当悬臂板相对宽度大于0.157时则相反,但FS箱梁跨中截面畸变角始终介于两者之间;SS 箱梁跨中截面畸变角单调增加,而FF箱梁和FS箱梁的则先增大后减小。随悬臂板相对宽度增大,SS 箱梁跨中截面畸变翘曲正应力发生变号,且3种边界条件下箱形梁的跨中截面计算关键点k1和k3的翘曲正应力变化规律不再相同;翘曲正应力边界影响系数变化剧烈,ζFS能达到15,ζFF甚至大于25,即随悬臂板相对宽度变化,FS 箱梁跨中截面畸变翘曲正应力能达到SS 箱梁对应值的15 倍,而FF 箱梁跨中截面畸变翘曲正应力能达到SS 箱梁对应值的25 倍以上。这说明如果带悬臂板的箱形梁其悬臂板宽度取值不合理,边界条件会对跨中截面翘曲正应力产生巨大影响。

图9 悬臂板相对宽度对跨中截面畸变效应的影响Fig.9 Influence of relative width of cantilever slab on distortion effect of midspan
4 结论
1)导出了3种不同边界条件下箱形梁在偏心均布荷载作用下的畸变效应解析解,建立ANSYS模型验证了所推公式的正确性,引入畸变效应边界影响系数分析了不同边界约束条件对箱形梁畸变效应的影响。
2)梁端约束越强,畸变效应纵向分布曲线越陡峭,当截面几何参数变化时,边界约束条件对畸变角的影响较小。
3)高宽比越大,畸变效应边界影响系数越小;当高宽比大于1.06 时,翘曲正应力边界影响系数比较接近,即当高宽比大于1.06 时,边界约束对翘曲正应力的影响会减小。
4)悬臂板相对宽度对翘曲正应力边界影响系数的影响较大,当相对宽度小于0.25 时,翘曲正应力变化较大。
