基于里兹法的高速铁路桥梁横向变形与轨面变形解析模型研究
2022-01-26刘丽丽蒋丽忠刘祥周旺保聂磊鑫邵光强
刘丽丽,蒋丽忠,刘祥,周旺保,聂磊鑫,邵光强
(1.中南大学土木工程学院,湖南长沙,410075;2.中南大学高速铁路建造技术国家工程实验室,湖南长沙,410075;3.中南大学重载铁路工程结构教育部重点实验室,湖南长沙,410075)
铁路运输具有速度快、运量大、安全舒适、减排高效等特点,在促进地域经济发展、加快资源开发和物资输出、推动社会经济和文化发展等方面具有特殊的地位和作用。我国高速铁路正处在迅猛发展时期,2018年底,“四纵四横”的高速铁路网已全面建成,预计到2025年,我国将形成“八纵八横”的高速铁路网。随着我国高速铁路网络的不断扩大,处在地震活跃带、极端气候和特殊地质条件等恶劣环境中的高速铁路距离将越来越长,桥梁结构在高铁线路中占的比例将越来越大。高铁桥梁在长期运营过程中将不可避免地产生桥墩沉降、梁体错台、梁体徐变上拱、梁端转角、支座变形等多种变形模式。大量研究表明,这些变形将会通过桥梁−轨道层间相互作用机制映射至轨面,从而引起钢轨变形。这种轨面附加不平顺将会对高速行驶的列车产生激扰,速度越快,激扰越大。随着人们对速度和舒适度要求的提高,研究梁体变形与高速列车的动力特性之间的关系至关重要,而进行这些研究的前提是准确了解梁体变形与轨面几何形态的映射关系。
近年来,JIANG 等[1−11]对高速铁路基础沉降变形对轨面几何形态的影响进行了大量研究,但大多集中于基础沉降对高速列车运行性能的影响。肖威等[10−11]分析了基础不均匀沉降变形对轨道板动力特性的影响;唐进锋等[12]研究了基础沉降变形对高速列车−CRTS Ⅲ型轨道板动力特性的影响规律。随着桥梁结构在铁路系统中占比不断增大,越来越多的研究者[13−14]对桥梁结构变形与钢轨变形的关系展开了研究。FENG等[14]提出了CRTS II轨道板−连续梁桥系统中梁体竖向变形与钢轨变形的映射关系解析解;GOU 等[13]提出了CRTS I 轨道板−简支梁桥系统中桥墩沉降和梁体竖向错台变形与钢轨变形的通用映射解析模型,并对其解析模型进行了验证。在此基础上,XIONG 等[6,15−20]进一步研究了桥墩沉降和梁体竖向错台变形对列车行车性能的影响规律。HOU 等[19]针对某地面塌陷区上的高速铁路简支梁桥系统,分析了在桥墩不均匀沉降作用下高速列车的动力响应,发现在地表下沉情况下,速度是影响高速列车运行安全稳定的主要因素。徐庆元等[21−22]根据梁体变形对行车性能的影响以及人们对行车安全性舒适性指标的要求提出了相应变形限值;CHEN等[22]在综合考虑多种因素的基础上提出了桥墩沉降的限值。随着人们对桥梁变形认识的加深,勾红叶等[23−26]对桥梁横向变形情况下钢轨的几何形态变化规律以及车辆动力响应特性进行了研究。高速铁路桥梁在各种复杂环境因素影响下,除了发生梁体的竖向变形之外[27−30],还会发生横向变形甚至2 个方向共同变形等情况。目前,国内外学者对竖向变形的研究较横向变形多。本文将针对常见的高速铁路32 m 简支梁桥−路基−CRTS Ⅲ板式无砟轨道系统,结合桥梁−路基−轨道层间相互作用机制,基于势能驻值原理,推导梁体横向变形与轨面几何形态的通用映射解析表达式,并进一步定量研究梁体横向错台和横向转角变形幅值对轨面几何形态的影响规律。
1 梁体变形与轨面变形的映射关系
1.1 机理分析和基本假设
高速铁路32 m 简支梁桥−CRTS Ⅲ板式无砟轨道系统从上到下依次由钢轨、扣件、轨道板、自密实混凝土填充层、底座板、梁体(路基)、支座、桥墩等结构组成,如图1所示。根据CRTS Ⅲ型板式无砟轨道单元式的铺设方式以及特殊构造,当梁体产生横向错台或转角变形时,CRTS Ⅲ板式无砟轨道系统将会跟随梁体产生相应变形,该变形将会引起扣件产生内力,进而导致钢轨发生形变。

图1 8跨32 m高速铁路简支梁桥−CRTS Ⅲ板式无砟轨道系统构造Fig.1 Simply-supported bridge−CRTS ⅢSBT structure of 8-span 32 m high speed railway
图2所示为简支梁桥某跨梁体发生横向错台变形时的俯视图。根据高速铁路32 m 简支梁桥−CRTS Ⅲ板式无砟轨道系统的结构特点,进行如下基本假设:

图2 梁体横向错台变形俯视图Fig.2 Top view of beam transverse fault deformation
1)底座板与梁体之间的预埋钢筋及底座板与轨道板之间的自密实混凝土等层间构件具有较强的横向约束效应,梁体和轨道板系统横向变形协调。
2)桥梁横向抗弯刚度远大于钢轨的横向抗弯刚度,忽略钢轨对梁体变形的影响。
3)钢轨两端简化为简支边界,通过取足够的路基段计算长度消除路基段钢轨边界效应。
1.2 映射关系基本方程
高速铁路简支梁桥−CRTS Ⅲ板式无砟轨道系统从左到右依次为路基、简支梁桥和路基,以左边路基的左端为坐标原点,建立整体坐标系。假定每跨标准32 m 简支梁上各布置M块轨道板,每个轨道板上有N个扣件,则共有M×N个扣件。
设梁体结构变形函数为ω2(x),对应扣件位置的梁体结构变形函数为ω2(xi)。将对应扣件位置梁体的变形表示成位移矩阵Ω2,可根据变形类型和变形幅值直接给出,不发生变形的梁体变形量为0 mm,梁缝处的钢轨变形与钢轨的整体变形相协调。设钢轨的变形函数为ω1(x),取正弦函数为基函数,则钢轨的变形曲线可近似表示为

式中:Am(m=1,…,n) 为常系数;lg为钢轨总长度。
由假设3)可知,钢轨边界条件可表示为

则当高速铁路简支梁桥−CRTS Ⅲ板式无砟轨道系统梁体发生横向变形时,钢轨在扣件力作用下的总势能Π可表示为
取土深度2.0m范围内,新安北堤、障水埝、四门堤及淀南新堤筑堤土料的岩性以土壤为主,局部为砂壤土及粉质黏土。
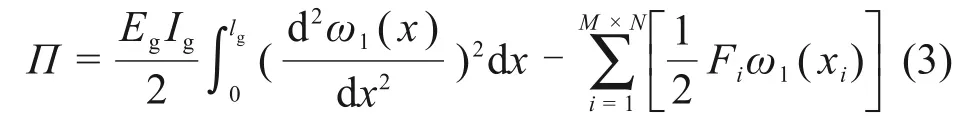
式中:Fi(i=1,2,…,M×N)为第i个扣件的扣件内力;Eg为钢轨弹性模量;Ig为钢轨的等效截面惯性矩。
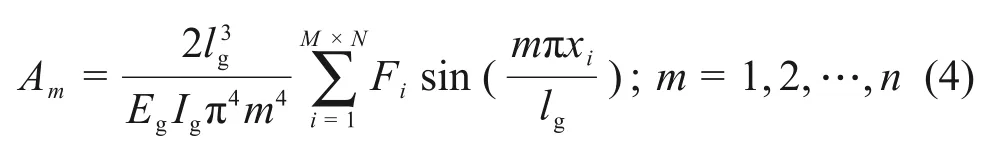
进而求得ω1(x),则扣件位置的钢轨位移向量可表示为

其中:F为扣件力向量;Ω1为扣件位置的钢轨位移向量;A为扣件力对钢轨位移的影响系数矩阵。
设ks为扣件横向等效刚度,则扣件内力向量可表示为

联立式(5)和(8)可得层间扣件内力向量为
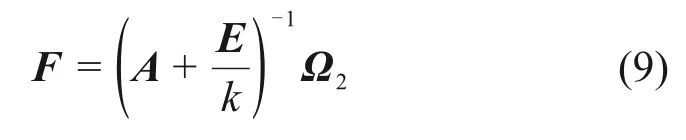
式中:E为与A同维数的单位矩阵。
则钢轨随简支梁梁体横向变形的映射关系为
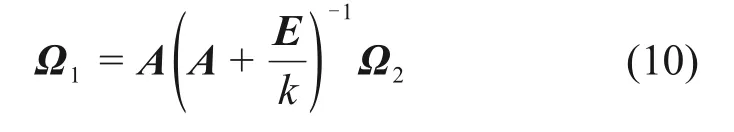
2 映射解析模型的验证
为验证映射解析模型的正确性,利用ANSYS有限元软件建立考虑路基的8 跨高速铁路32 m 简支梁桥−CRTS Ⅲ板式无砟轨道系统的有限元模型,利用该有限元模型计算系统在梁体横向错台、梁端横向转角下的钢轨变形,并与解析模型计算结果进行对比验证。
建模时,钢轨、轨道板、梁体及桥墩均采用beam3单元模拟,扣件、自密实混凝土填充层及支座均采用combine14弹簧单元模拟,墩底与路基段采用全约束,梁体横向错台以及梁端横向转角均采用位移约束实现。有限元模型中钢轨弹性模量取206.0 GPa;轨道板选用C60 混凝土,弹性模量取36.0 GPa;底座板选用C40混凝土,弹性模量取32.5 GPa;梁体选用C50 混凝土,弹性模量取34.5 GPa;扣件横向弹簧刚度取50 MN/m;自密实混凝土填充层横向弹簧刚度取为1.14×1012N/m,梁间距以及底座板间距均取20 mm。根据标准CRTS Ⅲ板式无砟轨道尺寸可知,轨道板间距为70 mm,各构件的材料性能如表1所示。

表1 桥梁和轨道系统各个构件的材料和性能Table 1 Materials and properties of each component of the bridge and track system
2.1 梁体横向错台变形与钢轨变形之间映射关系
梁体横向错台变形俯视图如图3所示。假设8跨高速铁路32 m 简支梁桥−CRTSⅢ板式无砟轨道系统在地震、板壳运动等自然灾害情况下[31−32],第2 号和第3 号相邻两桥墩发生同步水平移动,使第4 跨梁体发生3 mm 的横向错台变形,其余梁体保持正常。利用有限元模型和本文解析模型对该工况下的钢轨变形与扣件内力进行计算,计算结果分别如图4和图5所示。

图3 梁体横向错台变形俯视图Fig.3 Top view of beam transverse fault deformation
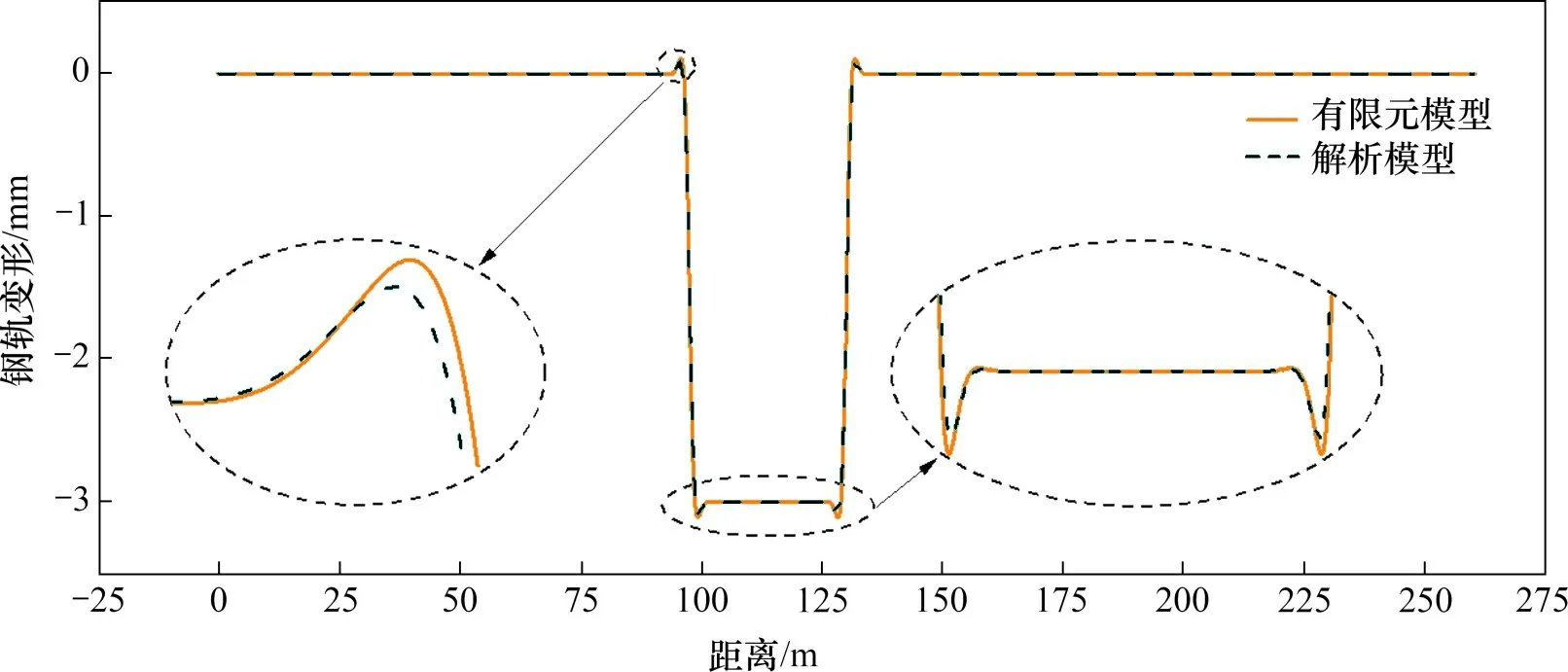
图4 第4跨梁体发生3 mm横向错台变形时的钢轨变形Fig.4 Rail deformation when the 4th span beam is deformed by 3 mm transverse fault deformation

图5 第4跨梁体发生3 mm横向错台变形时的扣件内力Fig.5 Fastener internal force when the 4th span beam is deformed by 3 mm transverse fault deformation
由图4和图5可知:在第三跨梁体发生横向错台变形工况下,解析模型和ANSYS有限元模型关于钢轨变形及层间扣件内力的计算结果吻合良好,验证了本文映射模型的正确性。由图4可知:钢轨在第3跨梁体横向错台工况下,映射变形曲线左右具有对称性;在梁体错台区域外,钢轨变形迅速减小直至为0 mm;在进出错台区域时,钢轨映射变形曲线呈现上翘及下凹现象,这将对高速列车的运行安全和乘坐舒适性产生不利影响;在梁体错台区域内,钢轨最大变形量略小于梁体最大变形量。
2.2 梁体横向转角变形与钢轨变形之间的映射关系
梁体横向对称转角变形俯视图如图6所示。假设第4跨和第5跨梁体梁端发生0.5×10−3rad横向对称转角变形,其余梁体均无变形。利用有限元模型和本文解析模型对该工况下的钢轨变形与扣件内力进行计算,计算结果分别如图7和图8所示。

图6 梁体横向对称转角变形俯视图Fig.6 Top view of beam transverse symmetrical rotation deformation
由图7和图8可知:在第3 跨和第4 跨梁体梁端发生横向对称转角变形工况下,基于解析模型和ANSYS有限元模型的钢轨变形曲线以及层间扣件内力曲线均吻合良好,进一步论证了本文解析方法的正确性;与有限元数值模型相比,解析表达式可以更直观地描述影响钢轨变形的影响因素,节省ANSYS建模和运算时间,同时可以清晰地表达各个因素与轨面几何形态之间的关系,物理意义更加明确[33−34]。

图7 第4和第5跨梁体发生0.5×10−3 rad横向对称转角变形时的钢轨变形Fig.7 Rail deformation when the 4th and 5th span beam are deformed by transverse symmetrical rotation deformation

图8 第4和第5跨梁体发生0.5×10−3 rad横向对称转角变形时的扣件内力Fig.8 Fastener internal force when the 4th and 5th span beam are deformed by transverse symmetrical rotation deformation
3 轨面变形的影响因素分析
3.1 梁体横向转角幅值对轨面变形的影响
由已验证的梁体变形与钢轨变形间映射解析表达式可知,影响桥梁−轨道映射关系的关键因素主要有梁体横向错台幅值、梁体横向转角幅值和扣件横向刚度等。为了研究梁体横向转角幅值对钢轨映射变形的影响规律,仍以考虑路基的8跨高速铁路32 m简支梁桥−CRTS Ⅲ板式无砟轨道系统为例,基于已验证的桥梁−轨道映射关系解析模型,分析第三跨梁体在发生不同梁体横向转角幅值时的轨面变形规律。在保持其他参数不变前提下,梁端横向转角的变化范围为0.5×10−3~3.0×10−3rad,增幅为0.5×10−3rad。不同梁端横向转角幅值下钢轨变形和层间扣件内力解析计算结果分别如图9和图10所示。钢轨向前变形幅值及向后变形幅值与梁体横向转角幅值之间的关系如图11所示。
从图9可以看出:在不同梁体横向转角变形幅值下,钢轨变形曲线均与梁体变形形状基本保持一致,表明在梁体横向转角变形工况下,钢轨变形具有良好的跟随性。对比图9和图10可以看出:钢轨变形量与层间扣件内力关系密切;层间扣件内力主要集中在梁缝中心线两侧,扣件内力随梁端横向转角幅值的增大而增大;扣件内力在第3跨左端和第四跨右端剧烈变化,两处扣件内力幅值接近相等且近似对称,在梁端转角处及第3跨右端梁缝处达到最大。从图11可以看出:随着梁端横向转角变形幅值增大,钢轨向前变形幅值及向后变形幅值近似呈线性增大,这说明在一定程度上可以通过控制梁端横向转角幅值来保证列车行驶的平顺度。

图9 不同梁体横向转角变形幅值下的钢轨变形Fig.9 Rail deformation under different transverse rotation deformation amplitudes of beam

图10 不同梁体横向转角变形幅值下的扣件内力Fig.10 Internal force of fastener under different transverse rotation deformation amplitudes of beam

图11 钢轨变形幅值与梁体横向转角变形幅值的关系Fig.11 Relationship between amplitude of rail deformation and transverse rotation deformation amplitudes of beam
3.2 梁体横向错台幅值对轨面变形的影响
为探明梁体横向错台幅值对钢轨映射变形的影响规律,仍以考虑路基的8 跨高速铁路32 m 简支梁桥−CRTS Ⅲ板式无砟轨道系统为例,分析第三跨梁体分别发生0.5,1.0,2.0,3.0,4.0 和5.0 mm 的梁体错台时钢轨变形及扣件内力的变化规律。不同横向错台幅值下钢轨变形和层间扣件内力计算结果分别如图12和图13所示,钢轨向前变形最值及向后变形最值与梁体横向转角幅值之间的关系如图14所示。
从图12可以看出:在不同梁体横向错台幅值下,钢轨变形曲线均与梁体变形形状基本保持一致,钢轨变形曲线具有对称性。从图13可知:在进出错台区域,扣件内力迅速增大,在发生错台梁体内,扣件内力迅速减小直至为0 kN。对比图12和图13可以看出:钢轨变形和层间扣件内力关系密切,即在钢轨发生急剧变形处,扣件内力亦急剧变化。从图14可以看出:随着梁体横向错台变形幅值增大,钢轨向前变形幅值和钢轨向后变形幅值近似呈线性增大,其中钢轨向前变形幅值变化范围极小,钢轨向后变形幅值与横向错台幅值相近,且略小于错台幅值。

图12 不同梁体横向错台变形幅值下钢轨变形Fig.12 Rail deformation under different transverse fault deformation amplitudes of beam

图13 不同错台幅值下的扣件内力Fig.13 Fastener internal force under different transverse fault amplitudes
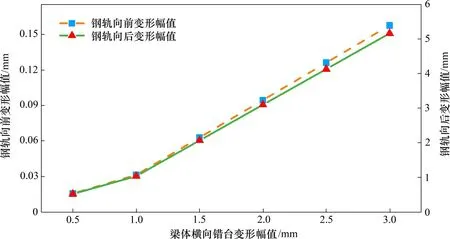
图14 钢轨变形幅值与梁体横向错台变形幅值的关系Fig.14 Relationship between amplitude of rail deformation and transverse fault deformation amplitudes of beam
3.3 扣件横向刚度对轨面变形的影响
为探明钢轨扣件刚度变化对钢轨映射变形的影响规律,仍以8 跨高速铁路32 m 简支梁桥−CRTS Ⅲ板式无砟轨道系统为例,分析第三跨梁体发生3 mm 横向错台、第五跨梁体发生2 mm 横向错台时,钢轨变形及扣件内力在不同扣件横向刚度(10,25,35,45 和55 kN/mm)时的变化规律。不同扣件横向刚度下钢轨变形和层间扣件内力计算结果分别如图15和图16所示。

图15 不同扣件横向刚度下钢轨变形Fig.15 Rail deformation under different fasterner transverse stiffness
从图15和图16可以看出:在不同扣件横向刚度下,钢轨变形曲线均与梁体变形形状基本保持一致,钢轨变形曲线具有对称性,且随着扣件横向刚度增大,钢轨变形幅值和扣件内力幅值增大不明显。从图15和图16中的局部放大图可以看出:随着扣件横向刚度增大,钢轨变形幅值、钢轨变形区域长度及扣件内力均小幅度增大。

图16 不同扣件横向刚度下的扣件内力Fig.16 Fastener internal force under different fastener transverse stiffness
4 结论
1)解析模型与ANSYS有限元模型在多种梁体变形工况下的钢轨变形对比结果论证了本文解析模型的正确性。
2)钢轨变形最值(最大值、最小值)与梁体横向转角变形幅值呈正相关关系。在进出横向转角区域,层间扣件内力发生突变,扣件内力幅值与梁体横向转角幅值呈正相关关系。
3)钢轨变形幅值与梁体横向错台幅值呈正相关关系。在进出错台区域,层间扣件内力发生突变,扣件内力最值(最大值、最小值)与梁体横向错台幅值呈正相关关系。在非梁缝区域内,层间扣件内力几乎为0 kN。
4)在不同梁体横向变形模式下,钢轨的变形形态不同。钢轨几何形态取决于梁体横向变形模式,扣件内力在梁体横向变形起始位置出现突变。
5)扣件横向刚度对钢轨变形幅值和扣件内力幅值影响不明显。随着扣件横向刚度增大,钢轨变形幅值、变形区域长度及扣件内力小幅度增大。
