自流式空气除尘系统管道中过饱和度分布特征
2022-01-26代安稳张军尹杰叶晓辉
代安稳,张军,尹杰,叶晓辉
(东南大学能源与环境学院,江苏南京,210096)
PM2.5是雾霾的重要成分,控制PM2.5仍是环境领域研究的热点[1−3]。由于PM2.5排放源多,排放过程和规模差异大,分布分散,且部分处于移动状态[4−6],因此,要从源头控制PM2.5的排放投入的资金大、见效时间长[7]。此外,控制大气中的PM2.5的多种技术得到了广泛应用中,主要包括过滤除尘技术[8−10]、静电除尘技术[11−12]、负离子净化技术[13−14]和湿式除尘技术[15]。但这些技术由于空气流动需依靠外力,运行成本高,只能应用于较小规模的室内空气的处理。而对需要对局部区域(如城市中心)空气进行处理时,目前大多采用处理效率低、耗能大的喷水雾方式。
HERING 等[16−19]提出了一种自流式空气除尘系统,其主要特点是:空气通过自然对流方式流经除尘系统,利用水汽相变技术使空气中的细颗粒物长大进而被脱除。在自流式空气除尘系统中,水汽过饱和环境是影响除尘效果的重要因素。本文以典型的高温热水与低温空气接触的方式构建过饱和场,通过FLUENT 软件研究所建系统中影响过饱和环境的主要因素,以期为该除尘技术的研发提供理论依据。
1 系统简介
图1所示为自流式空气除尘系统的示意图,由图1可见:自流式空气除尘系统主要包括3 个部分:循环水、除雾器和相变生长室。工作流程如下:

图1 自流式空气除尘系统的示意图Fig.1 Schematic diagram of gravity air dust removal system
1)来自太阳能加热器的热水在重力的作用下沿相变生长室壁面流下,由于热扩散及自然对流的作用,空气会自下而上流经相变生长室,与壁面的热水进行热质交换形成过饱和场。
2)空气中的细颗粒物在过饱和场中凝结长大,然后通过除雾器脱除,洁净的空气从生长管上方流出。
3)热水从相变生长室下端流出,经过过滤器及水泵的作用流回太阳能加热器进行加热,从而实现水的循环利用。
2 模型建立
2.1 物理模型
本文主要研究系统相变生长室中过饱和场的影响因素,暂不讨论自流式空气除尘系统的经济性及具体应用场景。由于管状结构易于生产且气流的流动对称性较好,为此自流式空气除尘系统的相变生长室采用竖直圆管,物理模型如图2所示。管道壁面均匀分布着高温热水,在高温热水与环境温差所形成的自然对流作用下,低温空气从底端进入管道,与壁面上的热水进行传热传质。由于蒸汽在空气中的传质系数大于空气的热扩散系数,过饱和场会在管道中形成。

图2 构建过饱和环境管道示意图Fig.2 Schematic diagram of constructing a supersaturated environment pipeline
2.2 数学模型
对于圆管传热传质模型,可使用柱坐标系进行分析,并采用如下假设[17]:
1)管道中进口气流的温度和蒸汽分压分布均匀;
2)管道中管壁工作液体温度均匀、恒定;
3)由于所研究的过饱和度较低,达不到均相凝结,忽略蒸汽相变释放的潜热对空气温度的影响;
4)忽略生长管中的轴向热扩散和其他二次流的影响。
由此可得到管道中水蒸气分压力偏微分方程
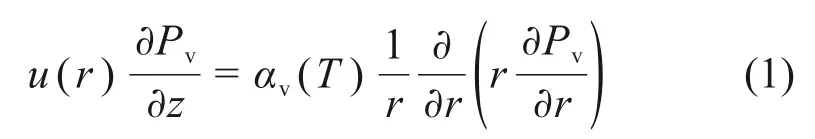
式中:u为空气流速;R为管道半径;r和z分别为径向距离和轴向距离;Pv为蒸汽分压力;αv为蒸汽质量扩散系数。
过饱和度S定义为蒸汽分压力Pv与蒸汽在气体绝对温度T下的饱和压力PT之比[20],即

2.3 Fluent二次开发模块
在Fluent默认求解连续性方程、动量方程和能量方程的基础上,使用UDS(user defined scalar)求解水蒸气分压力偏微分方程,并额外申请UDM用于存储计算中产生的中间变量,计算过饱和度。UDS是Fluent提供的一种用于求解用户自定义标量的模块,通过对比其标准输运方程,定义瞬态项、对流项、扩散项及源项来求解偏微分方程。
对于水蒸气分压力偏微分方程,不存在瞬态项及源项,只保留对流项和扩散项。与标准输运方程对比可得对流项为扩散项为
当流动情况为湍流时,总扩散系数为层流扩散系数加上湍流扩散系数,公式如下:

式中:Dl为层流扩散系数;ρ为流体密度;μt为湍流黏度;σ为湍流施密特数。
2.4 物性参数及边界条件
物性参数主要为空气密度、空气动力黏度、空气导热系数及水蒸气在空气中的传质系数,通过使用UDF改变流体物性。
由于空气流动动力来自于自然对流,对于空气密度的处理可采用BOUSSINESQ 假设[21]。BOUSSINESQ 认为除动量方程中的浮力项外,在其他所有求解的方程中都将密度视为常数。在温差ΔT<200 K 时,BOUSSINESQ 假设适用且能加快收敛[22]。
水蒸气在空气中的传质系数认为是温度和压力的函数[18]。空气动力黏度、导热系数等均按温度函数拟合。空气动力黏度μ和导热系数λ公式分别为[23]

式中:空气压力为0.1 MPa;T为空气温度;R′为相关系数。
本文研究所问题的瑞利数Ra在1011~1013之间,流动处于湍流状态(Ra<1010)[24],流动模型选用k-ε湍流模型。压力速度耦合采用SIMPLEC,压力、能量及UDS 迎风格式均采用二阶迎风,能量及UDS残差设定为10−9。
边界条件如下:进口采用压力进口边界,出口采用压力出口边界,壁面为wall 边界,本文求解柱坐标系下的偏微分方程,因此设定对称边界为axis;进口温度及壁面温度分别为Tin和Tw;进口及壁面的UDS 均设置为specified value,为当前温度下的饱和水蒸气分压力,出口UDS 设置specified flux为0。
2.5 模型的验证
本文需要对2个部分内容进行验证。1)流动状态为湍流且使用了UDS 功能,需要验证湍流情况下UDS代码的正确性;2)需要将UDS计算的过饱和场与其他文献进行对比,验证本方法计算过饱和场的正确性。
为了验证使用UDS 代码的正确性,本文使用Fluent自带求解器计算管道内的温度场,同时使用UDS计算温度场,对得到的结果进行对比。图3所示为湍流情况时,使用UDS 方法和使用Fluent 内嵌求解器计算出的管道中心处温度分布,由图3可见:湍流情况下,2 种方法计算的结果完全一致,说明本文使用UDS的求解方法正确。

图3 湍流时Fluent内嵌方法与UDS方法计算温度结果对比Fig.3 Comparison of temperature calculation results between Fluent embedded method and UDS method in turbulent flow
为验证使用UDS 方法计算的过饱和度的正确性,将模型尺寸及边界条件的选取与文献[17]保持一致,计算该工况下的过饱和度,两者结果对比如图4所示,过饱和度最大相对误差为3.67%,符合工程精度要求。

图4 Fluent UDS与文献[17]计算过饱和场结果对比Fig.4 Comparison of Fluent UDS and Ref.[17]calculation results of supersaturated field
3 过饱和度影响因素分析
在固定相变生长室长度为10 m 的条件下,研究生长室直径、热水引入位置、热水温度以及空气温湿度等对过饱和度的影响,其中,其他基本参数的基准值设定如下:管道直径d为0.15 m,进口空气温度为298 K,空气湿度为80%,壁面水温度为343 K,工作压力为0.1 MPa。
3.1 管道直径
考虑到管道尺寸标准及购买方便问题,在0.1~0.3 m 范围内选择不同直径的管道进行了计算。图5所示为不同管道直径下管道中心处过饱和度的分布特征。从图5(a)可见,随着管道直径d增大,过饱和度峰值基本相同,且出现位置逐渐接近管道出口;计算过饱和度方差发现,随着管径增大,管内过饱和度分布均匀性先减小后增加。这是因为热水及空气进口温度保持不变,热扩散系数及传质系数相同,随着管道直径增大,温度及水蒸气向管道中心扩散时间增大,过饱和度峰值的出现有一定延迟。过饱和度达到峰值前均匀性较差,达到峰值后均匀性较好。随着直径增大,过饱和度达到峰值的位置逐渐靠后,峰值前后的过饱和度均匀性均变好,但均匀性较差的部分比例增加,导致整体上均匀性下降。当管道直径增大到一定程度时,峰值前的过饱和度均匀性得到较大改善,导致过饱和度整体均匀性有所提高。
从图5(b)可见:随着管道直径增大,平均过饱和度先增加后降低。这是因为在管道直径较小时,过饱和度很快达到最大值,而后由于温度逐渐向管道中心扩散,饱和蒸汽压PT逐渐增大,过饱和度逐渐降低,此时管道的后半段过饱和度偏低。当管道直径逐渐增大,最大过饱和度向出口偏移,温度向管道中心扩散的时间增大,饱和蒸汽压PT增大幅度变小,管道后半段过饱和度下降趋势减缓,导致平均过饱和度升高。而当管道直径很大时,要经过很长的距离才能达到最大值,此时管道前段部分的过饱和度很低,因此平均过饱和度偏低。

图5 不同管道直径过饱和度的分布特征Fig.5 Distribution characteristics of supersaturation of different pipe diameters
3.2 空气温度
图6所示为热水温度Tw=343 K时,改变进口空气温度得到的过饱和度的分布特征。从图6(a)可见,过饱和度整体随着空气温度降低而增加,在较低空气温度时增加幅度更大,其峰值也在逐渐增大,但中心线处过饱和度的均匀性变差。这是因为热水温度不变时,液面上蒸汽分压力PV也保持不变,随着空气温度降低,管道内整体的温度水平T降低,对应的饱和蒸汽压PT下降,管道内整体过饱和度增加。由于饱和蒸汽压PT与温度呈指数关系,PT下降更加明显,所以,过饱和度的增加幅度在较低空气温度时更大。在过饱和度达到峰值后,壁面热水温度扩散到管道中心处,空气温度较低时,管道内高过饱和度迅速降低,造成均匀性变差,而空气温度较高时,中心线处过饱和度较低。因此,壁面热水温度的扩散对其影响并不大,其均匀性反而较好。

图6 不同空气温度下过饱和度的分布特征(Tw=343 K)Fig.6 Distribution characteristics of supersaturation at different air temperatures(Tw=343 K)
从图6(b)可见,随着进口空气温度降低,平均过饱和度增大,并在288 K时超过了水汽均相凝结的过饱和度界限值[25],因此,在冬季可适当降低热水温度来避免出现均相凝结。
3.3 热水温度
图7所示为空气进口温度Tin=298 K,改变管壁热水温度得到的过饱和度分布特征。由图7可见,随着热水温度增大,过饱和度整体趋势会往上移;平均过饱和度随壁面温度增加而增大。其变化原因与图6相同,在此不再赘述。同时从图6和7 可以看出,当温差过大即进口空气温度过低或热水温度过高时,管内中心线处的过饱和度可能会达到水汽均相凝结的过饱和度界限值,此时可能发生均相凝结,造成过饱和度偏小,但其分布特征即变化规律并未发生改变。
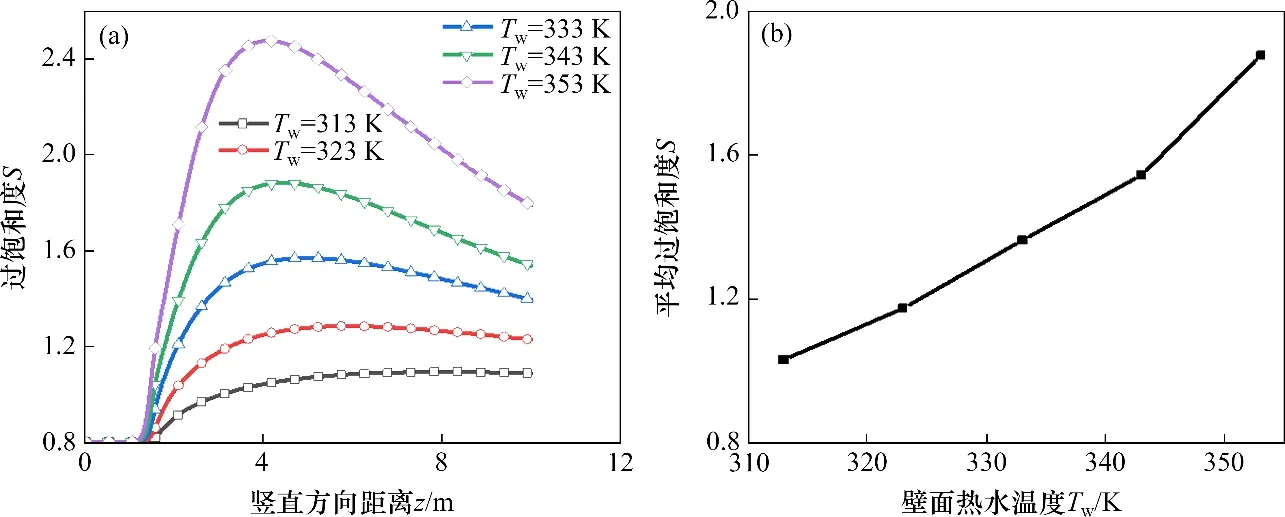
图7 不同热水温度下过饱和度的分布特征(Tin=298 K)Fig.7 Distribution characteristics of supersaturation at different hot water temperatures(Tin=298 K)
为了进一步研究改变空气温度和热水温度对过饱和度影响,将两者的平均过饱和度列于表1,对比发现,无论改变空气温度还是热水温度,相同温差时,平均温度水平较低的管道内平均过饱和度更大。如当ΔT=15 K 时,工况2(Tw=313 K,Tin=298 K)管道内的平均温度明显小于工况1(Tw=343 K,Tin=328 K)时的平均温度,因此,工况2 的平均过饱和度要大于工况1的平均过饱和度。这是因为温差相同时,蒸汽浓度差接近,但由于饱和蒸汽压PT与温度呈指数关系,当温度水平较低时,饱和蒸汽压PT的下降幅度更大,致使在较低的平均温度水平时平均过饱和度更大。

表1 温差相同时平均过饱和度结果对比Table 1 Comparison of mean supersaturation results with same temperature difference
3.4 进口空气湿度
图8所示为不同空气进口湿度下过饱和度的分布特征。从图8(a)可见,随着相对湿度增大,过饱和度的峰值逐渐增大,变化趋势整体上相同,且相对湿度的差异只在空气进口部分产生较大影响,对于管道中间及管道后半部分,这种影响会逐渐减小。进口空气相对湿度对中心线处过饱和度均匀性影响较小。这是因为管道内过饱和度的形成主要依靠水蒸气扩散,而不同相对湿度所引起的分压力的差距很小,因此不同的相对湿度下,过饱和度分布趋势相同。由于自然对流,空气进口部分仍处于层流,湍流扩散能力不强,越靠近出口,湍流越充分,湍流扩散系数越大,进口水蒸气分压力的影响越小。因此,在管道中间及管道后半段部分,不同相对湿度下的过饱和度差距越小。
由图8(b)可见:管道内平均过饱和度与进口空气相对湿度几乎呈线性关系。这是因为相同的进口空气温度下,进口空气的蒸汽分压力与相对湿度呈线性关系,而由于相对湿度只对管道进口部分的影响较大,对其他部分的影响较小,因此,平均的过饱和度与相对湿度呈近线性关系。
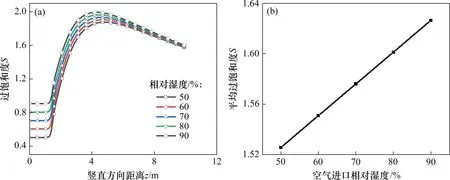
图8 不同进口空气湿度下过饱和度的分布特征Fig.8 Distribution characteristics of supersaturation under different inlet air humidity
3.5 热水加入位置
图9所示为热水加入位置对过饱和度的分布特征的影响,计算中认为未加入热水处的壁面温度为环境温度(Tin),壁面蒸汽分压力为0 Pa。从图9(a)可见:热水段的过饱和度分布曲线接近,而无热水段的过饱和度分布不同。当加入位置大于4 m即(z/L>0.4)时,过饱和度分布均与全覆盖(z/L=1.0)比较接近,且峰值相同。但当z/L<0.4,热水段长度较短时,无热水处过饱和度下降剧烈,且峰值有所降低。这是因为空气流动先经过热水段后经过无热水段,无热水段对热水段的过饱和度影响很小,因此热水段的过饱和度分布相近(如热水分段加入z/L=0.5,其前5 m 的过饱和度分布与全覆盖(z/L=1.0)前5 m的过饱和度分布相近)。
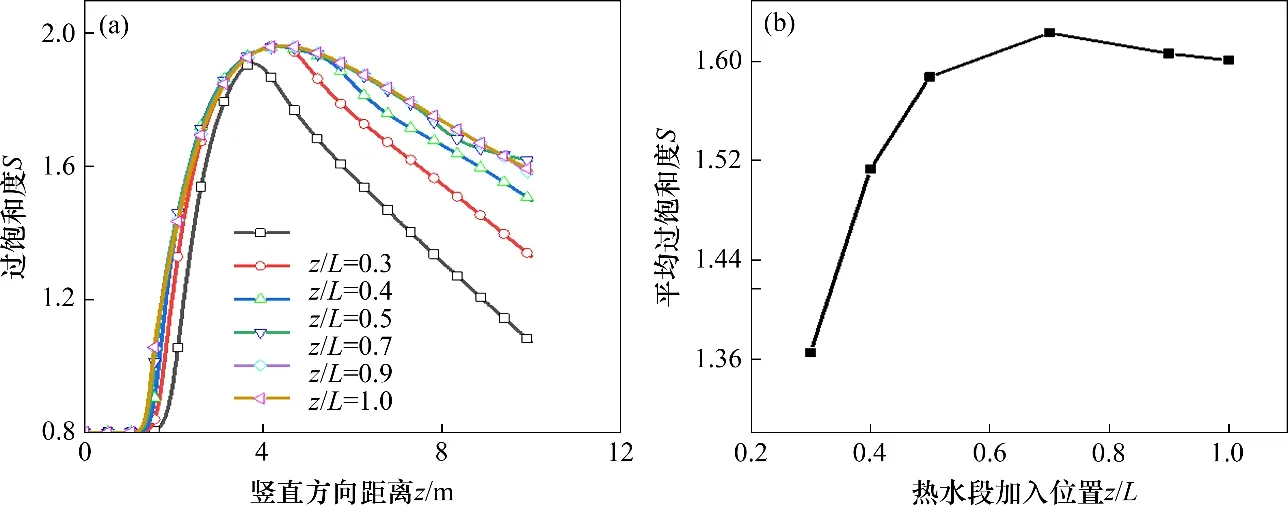
图9 不同热水加入位置过饱和度的分布特征Fig.9 Distribution characteristics of supersaturation at different hot water adding positions
当热水覆盖较短时(z/L<0.7),增大热水覆盖长度会提高过饱和度均匀性,但当热水覆盖较长时(z/L>0.7),增大热水覆盖长度反而会降低过饱和度的均匀性。这是因为z/L<0.7 时,过饱和度随着热水覆盖长度增加而增大,管道中心过饱和度曲线趋于平缓,过饱和度均匀性增强。但当z/L>0.7时,再增加热水覆盖长度反而会使出口处过饱和度降低,整体的过饱和度均匀性有所下降。
从图9(b)可见,随着热水加入位置提高,平均过饱和度先增大后减小。这是因为当热水段较短时尤其小于全覆盖峰值出现的位置(z=4 m)时,后半段的过饱和度急剧下降,因此平均过饱和度较低。当热水覆盖面更广时,后半段低蒸汽分压与低温度水平的共同作用,过饱和度下降并不明显,平均过饱和度增加。随着热水加入段位置z/L增大,后半段的温度及蒸汽分压力都变大,由于饱和蒸汽压PT与温度呈指数关系,因此温度对过饱和度的影响更显著,从而平均过饱和度降低。
4 响应面法分析
由于自流式空气除尘系统针对室外空气进行除尘,室外空气的温度和湿度无法人为控制,不能作为可控的工况参数进行优化,因此为研究方便,认为室外空气温湿度为恒定值,取近10 a 南京地区平均温度和湿度分别为291 K和70%,管道长度为10 m。在此基础之上,根据BBD 试验设计原理,在上述单因素数值模拟分析的基础上,进行响应面分析,确定各因素对过饱和度的影响程度。
4.1 因素与水平
以管道直径d、壁面热水温度Tw及热水加入位置z为自变量,以过饱和度S为因变量,进行三因素三水平响应面分析。表2所示为响应面试验设计的因素与水平值。
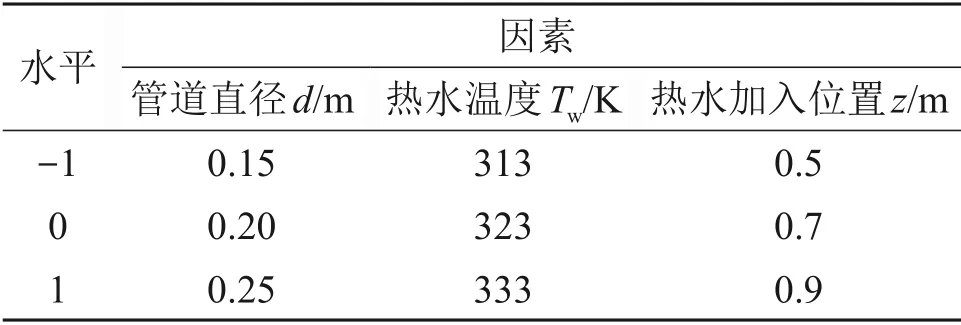
表2 响应面设计因素与水平Table 2 Response surface design factors and levels
4.2 响应面试验设计及结果
表3所示为Box-Behnken 试验设计与结果,有5 次重复试验,试验号分别为6,9,11,15 和16,对这5次试验网格调整后进行数值计算,以满足对失拟项显著程度的考察。
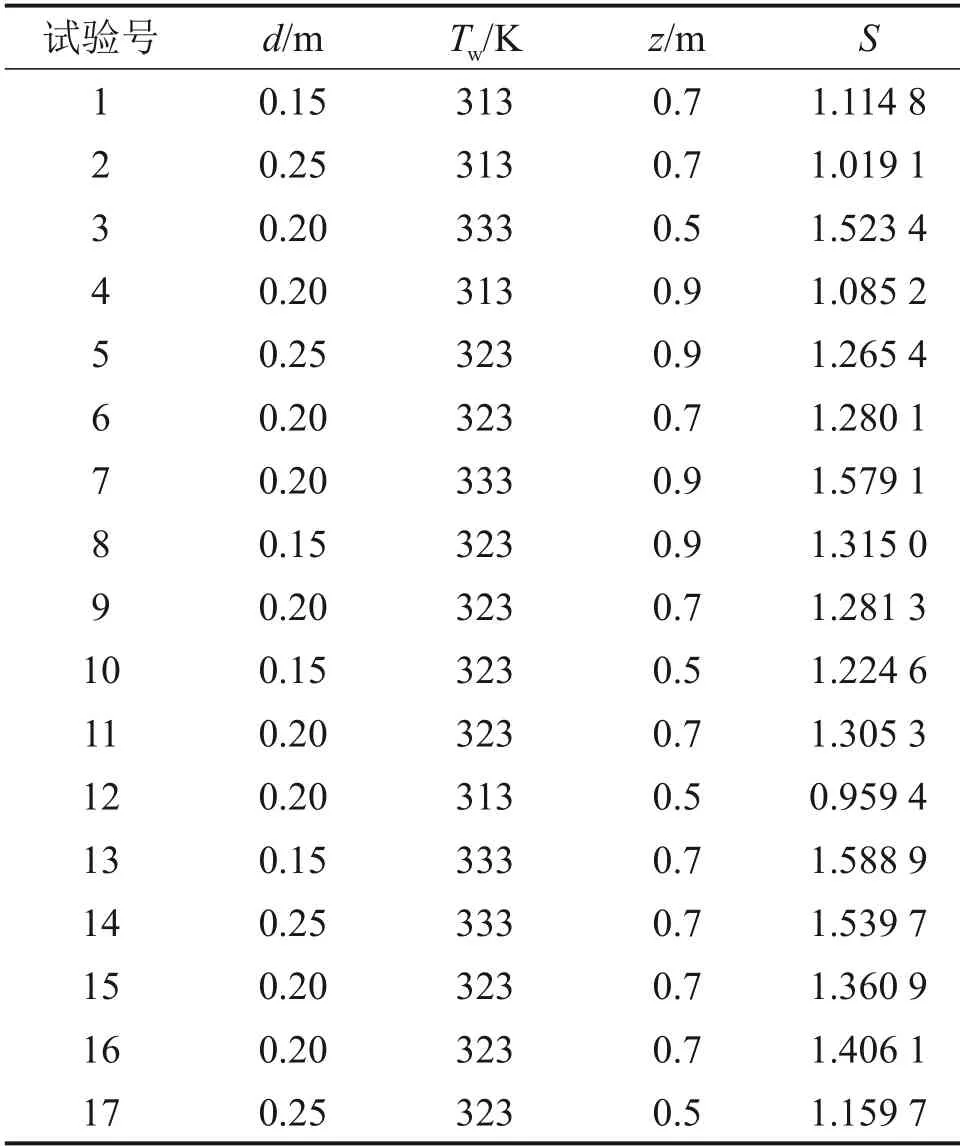
表3 Box-Behnken试验设计与结果Table 3 Box-Behnken test design and results
使用Design Export 12.0,以过饱和度为响应值进行了二次多元回归拟合,得到拟合回归方程为:

对拟合模型进行方差分析,得到表4。表4所示为过饱和度的显著性检验结果。相关系数的显著性可以用显著性检验结果可信程度的递减指标P来表示。模型的P<0.01表明该试验拟合的二次多项回归模型具有极高的显著性;失拟项P为0.977 1,多元相关系数为0.972 9,表明该模型的相关性好、拟合效果好且试验误差较小;校正决定系数为0.960 6,表明有96.06%响应值的变化可以通过该试验方法和结论建立的模型进行解释。Tw,z的P均小于0.01,表明热水温度及热水加入位置对响应值的影响极显著。d和z2的P小于0.05,说明各因素对响应值的影响较复杂,不是简单的线性关系。由F(Tw)>F(z)>F(d)可知,各因素对过饱和度的影响程度由强到弱依次为热水温度、热水加入位置和管道直径。同时F(Tw)远大于F(d)和F(z),说明热水温度对过饱和度的影响程度要远超过管道直径和热水加入位置的影响程度,管道直径和热水加入位置对过饱和度的影响程度相当。

表4 过饱和度Y回归模型方差分析Table 4 Variance analysis of supersaturation Y regression model
5 结论
1)当管道长度不变时,随着管道直径增加,管道内平均过饱和度呈现出先升高后降低的趋势;随着空气和热水温差增大,平均过饱和度会增大,但要想获得更大过饱和度,需要增大加热热水的能量,可能造成更大经济损失;相较于其他因素,进口空气相对湿度对管道平均过饱和度影响不大;相较于热水全覆盖,加入热水位置靠近管道出口有利于增加平均过饱和度。
2)空气与热水温差较低时,中心线处过饱和度均匀性较好,但过饱和度较低,因此不能简单通过降低温差来提高均匀性,可通过选择合适的管道直径及热水加入位置提高中心线处过饱和度均匀性。
3)对过饱和度的影响程度由强到弱依次为热水温度、热水加入位置和管道直径。因此,在选择工况参数时,应首先考虑热水温度对过饱和度的影响;对于相同温差的情况,可通过使用较低温度来获得较大过饱和度;管道直径及热水加入位置都存在最优值,针对不同工况选取合适的参数可使系统过饱和度最大。
