稀疏平衡变分自动编码器的文本特征提取 *

车 蕾

(北京信息科技大学 信息管理学院， 北京 100192)

随着各类语言模型层出不穷，人们开始将目光聚焦到模型最根本的表示层上。在机器学习中，特征学习(Feature Learning，FL)是将原始数据转换成机器学习能够处理的形式。原始数据通常为高维数据，高维数据既是维数福音，又是维数灾难，对机器学习算法提出挑战。特征学习的目的就是将高维的冗余的原始特征转换为低维的保留有效信息的特征[1]。特征学习包括特征选择和特征提取。区别于单纯选择子集的特征选择，特征提取是将原始表达投影到一个低维特征空间中以得到一个更加紧凑的表达[2]。本文研究工作是针对文本特征提取展开的。

目前研究存在如下问题：高维数据特征区分度较低、基于规则的特征学习的自学习和自适应能力差。深度学习则可以提高特征学习的自学习和自适应能力。本文将借助深度学习中变分自动编码器(Variational AutoEncoder，VAE)的潜变量研究文本特征提取的方法。潜变量产生即低维特征表示，但是训练过程中存在潜在损失过度剪枝(即KL(Kullback-Leibler)散度为零)的情况。在这种情况下，生成器倾向于完全忽略潜在表示并简化为标准语言模型[3]。解决此问题的最典型方法是使用KL项权重的模拟退火算法来权衡重构误差与KL散度的贡献[4]，但是此方法可能无法提高生成样本的质量，网络需要额外的容量来提高重构质量，代价是潜在空间利用率变低，很难被随机生成器利用。

为解决以上问题，本文提出一种稀疏平衡变分自动编码器(Sparse Balanced Variational AutoEncoder，SBVAE)的文本特征提取模型。本文简要说明变分自动编码器原理，分析降噪处理过程，详细阐述稀疏平衡性方法。本研究的实验选取代表性的真实数据集，从文本特征提取模型对比分析、稀疏性能分析、稀疏平衡处理对隐藏空间变分下界(Evidence Lower BOund，ELBO，也称为证据下界)的影响等几个方面深入开展，验证了SBVAE文本特征提取模型具有较好的性能。

1 相关工作

特征提取的常用传统算法有：概率模型、文档频率、信息增益等。传统方法特征识别度较低。基于概率模型的方法选择出来的词汇能够有效地代表类别，但可能会过滤掉代表性强但出现频率较低的词[5-6]；基于文档频率的方法有可能丢弃某些有特殊含义的低频词条，筛选时需要选择恰当的阈值[7]；基于信息增益的方法缺乏各特征词对特定文档的代表性考虑，实际应用效果很难达到理论效果[8-9]。

VAE模型是深度学习中的一种无监督表示学习和深度生成模型[10]。VAE具有与标准自动编码器(AutoEncoder，AE)完全不同的特性，它的隐含空间被设计为连续的分布以便进行随机采样和插值，这使得它成了有效的生成模型。VAE通过KL散度使潜变量分布靠近标准正态分布，从而能解耦潜变量特征，简化后续建立在该特征之上的模型，增强其泛化性能；另外，正态分布也使得编码空间更加规整。2013年，Kingma等提出VAE，它是深度生成模型，而不是基本的自动编码器[11]。

VAE模型在自然图像[12-13]和语音[14]生成方面取得了比较好的成果。目前，VAE模型在自然语言方面也取得一些进展。Wolf-Sonkin等基于VAE开展了上下文形态学拐点的研究[15]。Yang等基于VAE开展了文本建模的研究[16]。Li等基于VAE提出一种深度网络表示模型，无缝地集成文本信息和网络结构[17]。文献[16]和文献[18]基于VAE开展半监督分类的研究工作。Semeniuta等探讨了架构选择对学习文本生成的VAE的影响[3]。Louizos等基于VAE研究学习表示模型，该模型对于某些有害或数据变化的敏感因素是不变的，同时保留尽可能多的剩余信息[19]。目前VAE的研究主要是面向生成问题的，在文本特征提取方面的研究还比较少。VAE的主要优点是能够学习输入数据的平滑潜在状态表示，所以借助VAE的潜在空间研究文本特征提取问题是非常有价值的。但是，在足够高维度的潜在空间中，VAE存在过度剪枝的问题，倾向于忽略大量潜变量，即KL散度为零[20]。过度剪枝的做法可能会影响生成模型的质量。解决此问题的最典型方法是使用KL项权重的模拟退火算法来权衡重构误差与KL散度的贡献[4]。KL退火可以看成是从传统确定性自动编码器到完整VAE的逐渐过渡，但是这种方式很难被随机生成器利用。

2 模型

本文提出一种SBVAE文本特征提取模型。研究按如下步骤完成：

步骤1：采用词频-逆文档频率(Term Frequency-Inverse Document Frequency, TF-IDF)算法进行文本表示。

步骤2：针对数据量大、维度高的数据集，为提高数据的特征项明确度和分类精度，采用VAE进行文本特征提取。

步骤3：为提高鲁棒性，采取消除噪声干扰方法，在文本特征提取的输入层采用双向降噪处理机制。

步骤4：为缓解KL散度引发的过度剪枝的影响，并强制解码器更充分地利用潜变量，结合KL项权重的模拟退火算法提出一种稀疏平衡性处理方法。

步骤5：采用文本聚类算法验证文本特征提取的性能[21]。

2.1 变分自动编码器

自动编码器是利用人工神经网络的特点构造而成的网络[22]。自动编码网络，是由一组受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)按一定次序连接而构成的[22]。自动编码器的基本要求是保留原始数据的(尽可能多的)重要信息。当编码向量的分布尽可能接近高斯分布时，就导致了VAE的产生。VAE是一种将变分推理和深度学习相结合的潜变量生成模型，包括两部分：编码器和解码器[11]。相对于自动编码器，VAE做了两大改进：第一，输入x的由编码器提供的确定性内部表示z被后验分布qφ(z|x)替换。然后通过解码器将采样出来的z用于还原输入。为了简化采样过程，后验分布选择标准正态分布，其均值和方差由编码器预测。第二，为了确保可以从潜在空间的任何点进行采样并能产生有效、多样的输出，后验分布qφ(z|x)通过其与分布pλ(z)的KL散度进行正则化。通常，先验分布也选择标准正态分布，使得可以以封闭形式计算先验和后验之间的KL散度。VAE让所有的qφ(z|x)接近标准正态分布，不仅防止了噪声为零的情况，也保证了模型具有生成能力。VAE结构如图1所示。

图1 变分自动编码器Fig.1 Variational autoencoder

VAE是概率潜变量模型，通过条件分布将观察到的向量x与低维潜变量z相关联[23]。VAE模拟x的概率是：

(1)

其中：pθ(x|z)是给定z的x的条件分布，其由参数为θ的神经网络建模；pλ(z)是潜变量的先验，其由参数为λ的神经网络建模。这些神经网络称为解码器。

对数似然估计logpθ(x)的下界是来自Jensen不等式的ELBO[1]，如式(2)所示。

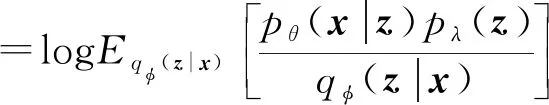
≡L(x;θ,φ)

(2)

ELBO也可以写成如下形式：

LVAE=L(x;θ,φ)

=Eqφ(z|x)[logpθ(x|z)]-DKL(qφ(z|x)‖pλ(z))

(3)

DKL(qφ(z|x)‖pλ(z))

(4)

其中，D为x的样本数量。损失函数包括两项：第一项是惩罚重构误差Eqφ(z|x)[logpθ(x|z)]，由于要从分布里采样，所以相对自动编码器多了个期望值运算符；第二项是相对熵DKL(qφ(z|x)‖pλ(z))，鼓励模型学习分布qφ(z|x)近似于真实的先验分布pλ(z)，即一般正态分布[24]。重构的过程是希望没有噪声的，而KL 散度则希望有高斯噪声，两者是对立的。KL损失函数鼓励所有编码围绕隐藏层中心分布，同时惩罚不同分类被聚类到分离区域的行为。利用纯粹KL散度损失得到的编码是以隐藏空间为中心随机分布的。但是解码器从这些无意义的表达中很难解码出有意义的信息。KL损失和重构损失结合起来就解决了这个问题。这使得在局域范围内的隐藏空间点维持了相同的类别，同时在全局范围内所有的点也被紧凑地压缩到了连续的隐含空间中。这一结果是通过重构损失的聚类行为和KL损失的紧密分布行为平衡得到的，从而形成了可供解码器解码的隐含空间分布。

2.2 降噪处理

为了提高VAE的鲁棒性和泛化性能，基于VAE从数据中学习到更有用的特征表示，本文对VAE进行双向降噪处理。在样本输入时加入了某种类型的噪声，使模型能够从受“污染”的部分输入中重构出“纯净”的输入，同时使模型能够从部分的“纯净”输入中反向重构出受“污染”的输入。即在降噪环节，首先随机选择一定比例的非0数据将其置为0，即随机的损坏处理，从而加入噪声；然后随机选择更小比例的0将其置为1，即随机的修复处理。这样可以使参数初始化尽量处于全局最优空间附近，避免进入局部最优参数空间。

2.3 稀疏平衡性处理

在足够高维的潜在空间中工作，网络学习表示的实际网络容量更加紧凑，许多潜变量独立于输入而被清零，并且完全被生成器忽略。当潜在空间的采样接近于1的时候，则认为它被激活，而采样接近于0的时候则认为它被抑制，使得神经元在大多数情况下都是被抑制的限制称为稀疏性限制。稀疏性限制可以让神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据的结构信息。VAE中的KL散度可以让高维潜在空间中的数据变得自然稀疏[25]，它充当了正则化的作用，具备稀疏性相关的典型优势：它强制模型专注于真正重要的特征，大大降低过度拟合的风险。特别是，它是正确调整模型容量的主要方法，逐步训练模型以获得稀疏性或者减少网络的维度以移除未使用的神经元的连接。

研究发现，在足够高维度的潜在空间中，VAE存在过度剪枝的问题，倾向于忽略大量潜变量，即KL散度为零。过度剪枝[20]的做法可能会影响生成模型的质量。解决此问题最典型的方法是使用KL项权重的模拟退火算法来权衡重构误差与KL散度的贡献，如式(5)[26]所示，其中α表示超参数。

LVAE=Eqφ(z| x)[-logpθ(x|z)]-αDKL(qφ(z|x)‖pλ(z))

(5)

KL退火可以看成是从传统确定性自动编码器到完整VAE的逐渐过渡，如式(5)所示，本研究也同时采取0到1的线性退火解决KL消失的问题。首先运行一个KL权重固定为0的模型，以找到它需要收敛的迭代次数；然后，将退火计划配置为在非正则化模型收敛后开始，持续时间不少于该数量的20%[3]。调低α可以控制不确定性，但是可能无法提高生成样本的质量，网络需要额外的容量来提高重构质量，代价是潜在空间利用率变低，很难被随机生成器利用。解决过度剪枝的另一个方法是修改模型架构，例如，文献[27]中提出了一种概率生成模型，该模型由许多称为缩影的稀疏变分自动编码器组成，这些缩影共享自动编码器的解码器架构。

本文采用一种平衡性方法缓解可能过度剪枝的影响。所提出的稀疏平衡是指为避免过度剪枝，在VAE的损失函数LVAE中加入一个辅助稀疏惩罚项，平衡潜在空间变量的稀疏化。稀疏平衡使潜在空间的采样均值尽量接近0.01～0.03之间的某个值，以便达到稀疏的目的。整个过程肯定会丢失信息，但训练能够使丢失信息尽量少。添加了辅助稀疏惩罚项后的VAE损失函数表达式如式(6)所示。

(6)

其中：α和β表示超参数；m表示隐藏神经元数目；后一项为KL距离，其表达式如式(7)所示。

(7)

(8)

其中：n表示输入向量数；zji表示隐藏神经元j对应第i个向量的激活度。为避免z为负值引起的LSBVAE无穷大，在输出之前需要对z值取sigmoid后再进行稀疏平衡处理。LSBVAE的目标函数对潜变量z施加了约束，以产生有效特征。

3 实验

实验分别从实验环境及数据、对比实验及参数设置、性能评价指标、实验结果与分析四个方面进行详细讨论。

3.1 实验环境及数据

为了验证模型的有效性，采用如下2种标准数据集(均可以通过开源网站获得)进行实验。

1)复旦数据(中文)[28]：复旦大学文本分类数据，此数据集由复旦大学计算机信息与技术系国际数据库中心自然语言处理小组提供。实验从中选取了3个话题，记录数为8 423条。实验数据集的分布情况如图2所示。

图2 复旦数据集数据分布Fig.2 Data distribution of Fudan dataset

2)路透社(英文)[29]：此新闻数据集是由路透公司采集的1987年的新闻稿组成的Reuters-21578文集作为实验数据集。实验从中选取了3个话题，记录数为6 740条。实验数据集的分布情况如图3所示。

图3 路透社数据集数据分布Fig.3 Data distribution of Reuters dataset

对采集到的中文文本进行如下预处理：首先采用结巴(jieba)分词工具对数据进行分词，并去除文本中的数字；接着过滤掉叹词、副词等相关性较弱的词语和标点符号；最后去除停用词。对采集到的英文文本进行如下预处理：去除数字和停用词；字母全部转为小写；用Porter算法进行词干化处理，将英文中单复数、时态等变形词转换成原型。所有字符编码采用无BOM的UTF-8格式。

3.2 对比实验及参数设置

本文选取了6个模型进行对比实验，以便验证本文提出的模型的性能。具体模型信息如下：①主成分分析(Principal Component Analysis，PCA)；②AE；③稀疏自动编码器(Sparse AutoEncoder，SAE)；④VAE；⑤降噪变分自动编码器(Denoising Variational AutoEncoder，DVAE)；⑥SBVAE。

本实验的训练参数是通过多次实验获得的最优参数。因为实验涉及的是多分类问题，所以交叉熵采用的是Categorical_Crossentropy。最大epoch为500，基础学习率为0.001。实验训练采用的是自收敛方式，当损失值变化连续n次都低于某个临界值(默认0.000 1)时，训练自动终止。编码器和解码器都采用完全连接网络。模型采用Keras的自适应优化器Adadelta，允许在每个步骤中为学习率计算不同的值，以使训练效果达到最优。

3.3 性能评价指标

实验通过采用K-means聚类算法验证特征提取的性能。性能评价指标包括：准确率、召回率、F1值、熵和纯度。准确率、召回率、F1值和纯度越高越好，熵值越低越好。

1)准确率：预测正确的结果占总样本的百分比。

2)召回率：在实际为某类的样本中被预测为该类样本的概率。

3)F1值：同时考虑准确率和召回率，让两者同时达到最高，取得平衡。计算公式如下：

(9)

(10)

(11)

5)纯度：使用上述熵中的pij定义，聚类i的纯度定义如式(12)所示，整个聚类划分的纯度如式(13)所示。

pi=max(pij)

(12)

(13)

3.4 实验结果与分析

通过比较实验和可视化实验，将已有的算法与本文提出的SBVAE算法进行对比，展示本算法的优势；通过实验，展示基于SBVAE的文本特征表示对聚类过程的贡献，以更好支持后续话题检测与追踪工作的研究。

3.4.1 实验结果对比分析

本节是基于SBVAE文本特征提取模型开展的聚类实验。表1是基于复旦数据集的实验结果比对，表2是基于路透社数据集的实验结果比对。从表1可以看出，SBVAE的F1值依次比PCA、AE、VAE的F1值提升了12.36%、1.12%、0.47%。从表2可以看出，SBVAE的F1值依次比PCA、AE、VAE的F1值提升了8.06%、5.07%、3.42%。实验结果显示，不论是复旦数据集，还是路透社数据集，本文提出的SBVAE文本特征提取方法都能得到纯度较高的聚类效果，证实了该方法具有一定的稳定性。

表1 复旦数据的实验结果对比

表2 路透社数据的实验结果对比

图4和图5基于复旦数据集分别展示了二维空间下原始标注数据的分布和SBVAE特征提取(F1值为0.962 1)后K-means聚类效果。可以发现，图5的聚类效果较好，纯度较高，说明本文提出的SBVAE特征提取模型具有较好的性能。

图4 原始标注的复旦数据Fig.4 Fudan dataset of original annotation

图5 SBVAE特征提取后K-means聚类效果图Fig.5 K-means Clustering effect after feature extraction based on SBVAE

3.4.2 稀疏性实验

图6 SAE中的训练轨迹(ρ=0.01)Fig.6 Training track of in SAE(ρ=0.01)

图7 SAE中的训练轨迹(ρ=0.05)Fig. 7 Training track of in SAE(ρ=0.05)

图8 SBVAE中的训练轨迹(ρ=0.01)Fig. 8 Training track of in SBVAE(ρ=0.01)

图9 SBVAE中的训练轨迹(ρ=0.05)Fig.9 Training track of in SBVAE (ρ=0.05)

图10～19显示的实验结果取的是VAE和SBVAE训练结束时的各文本隐藏空间对应的潜变量z、方差和均值。潜变量z、方差和均值都为向量，因此这里取的是向量各维度的均值构建的图例。相关公式如下：

(14)

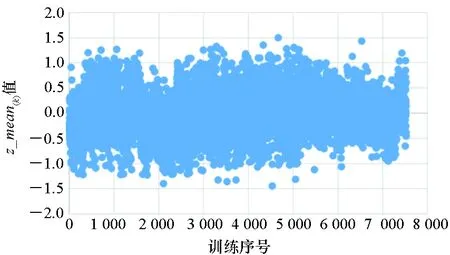
图10 VAE的潜变量z_mean(k)分布(散点图)Fig.10 Distribution of latent variables z_mean(k) in VAE (scatter plot)

从图10、图11、图15和图16大致可以看出，稀疏平衡之前的潜变量z在0附近的密集程度要略低于稀疏平衡之后的潜变量z在0附近的密集程度。本实验的潜变量z的个数为7 524，隐藏空间维度为50，总向量值个数为376 200。实验统计，稀疏平衡之前潜变量z的向量值在-1与1之间的个数为91 601个，稀疏平衡之后潜变量z的向量值在-1与1之间的个数为93 830个。由此说明，稀疏平衡后潜变量z的稀疏程度大于稀疏平衡之前的稀疏程度。其中，排列图是指按频数的降序绘制数据的分布，累积线位于次坐标轴上，标识占总数的百分比。排列图的箱宽度是通过使用Scott正态引用规则计算的。从图12、图13、图17和图18稀疏平衡处理前后VAE中的方差分布情况可以看出，稀疏平衡后的潜在空间的方差逼近1的值也相对增多。从图14和图19稀疏平衡处理前后VAE中的均值分布情况可以看出，稀疏平衡后的均值逼近0的值也相对增多。

图11 VAE的潜变量z_mean(k)分布(排列图)Fig.11 Distribution of latent variables z_mean(k) in VAE (pareto diagram)

图12 VAE的σ_mean(k)分布(散点图)Fig.12 Distribution of σ_mean(k) in VAE(scatter plot)

图13 VAE的σ_mean(k)分布(排列图)Fig.13 Distribution of σ_mean(k) in VAE (pareto diagram)

图14 VAE的μ_mean(k)分布(排列图)Fig.14 Distribution of μ_mean(k) in VAE (pareto diagram)

图15 SBVAE的潜变量z_mean(k)分布(散点图)Fig.15 Distribution of latent variables z_mean(k) in SBVAE(scatter plot)

图16 SBVAE的潜变量z_mean(k)分布(排列图)Fig.16 Distribution of latent variables z_mean(k) in SBVAE (pareto diagram)

图17 SBVAE的σ_mean(k)分布(散点图)Fig.17 Distribution of σ_mean(k) in SBVAE (scatter plot)

图18 SBVAE的σ_mean(k)分布(排列图)Fig.18 Distribution of σ_mean(k) in SBVAE (pareto diagram)

图19 SBVAE的μ_mean(k)分布(排列图)Fig.19 Distribution of μ_mean(k) in SBVAE (pareto diagram)

综上所述，稀疏平衡后的特征提取性能优于稀疏平衡之前的性能。

3.4.3 稀疏平衡处理对隐藏空间变分下界的影响

为了验证模型引入稀疏平衡处理对变分下界的影响，表3显示了基于复旦数据集在SBVAE中设置隐藏空间维度为不同值时变分下界的变化情况。其中，惩罚重构误差项、KL散度1和KL散度2分别对应式(6)中等号右边的三个项，KL散度2即辅助稀疏惩罚项。

表3 SBVAE的变分下界

表4显示了基于复旦数据集在VAE中设置隐藏空间维度为不同值时变分下界的变化情况。其中，惩罚重构误差项和KL散度分别对应式(5)中等号右边的两个项。变分下界是越低越好。和VAE的变分下界相比，引入稀疏平衡处理后的VAE对变分下界(-logpθ(x)≤)有显著的提升，其变分下界优于标准的VAE模型的变分下界。

表4 VAE的变分下界

4 结论

本文提出了SBVAE文本特征提取模型。为提升高维数据的区分度，基于VAE研究文本特征提取问题；为消除噪声干扰，在输入层采用双向降噪处理机制；为缓解过度剪枝的影响，结合KL项权重的模拟退火算法提出稀疏平衡性处理，强制解码器更充分地利用潜变量。实验从多个方面深入开展，验证了SBVAE模型在文本特征提取问题的解决上具有较好的性能，对文本特征提取问题的研究具有一定的推动作用。

未来的工作方向将尝试把模型扩展到半监督学习中，学习潜变量的深度结构性分层，并进一步研究其推理方案。