毫米波非均匀平面阵列无损检测三维成像算法 *
2022-01-26马昭阳邓桂林王宏强
马昭阳,邓桂林,曾 旸,邓 彬,杨 琪,王宏强
(国防科技大学 电子科学学院, 湖南 长沙 410073)
毫米波是指波长为1~10 mm、频率为30~300 GHz的电磁波。与频率较低的微波相比较,毫米波可以获得更高的分辨率和更强的穿透性;与X射线相比较,毫米波波段的光子能量低,不会损害探测目标。因此,三维毫米波全息成像技术在无损检测中极具优势[1-2]。
毫米波全息成像系统主要包括基于平面阵列的成像系统和基于柱面阵列的成像系统。其中基于平面阵列的成像系统发展较成熟,已经被成功应用于各种领域,例如安全检查、无损检测、穿墙成像等[2-3]。由于收发天线均匀分布在平面中的二维单发单收(Two Dimensional Single Input Single Output, 2D-SISO)系统造价昂贵、难以普及,将其中一维用扫描方式替代实现的一维单发单收一维扫描(One Dimensional Single Input Single Output One Dimensional Scanning, 1D-SISO-1D-scanning)系统得到了广泛的研究和应用[4-6]。
另外,研究者们开始探索通过设计非均匀阵列提高成像效率[7-9]。在这种情况下,回波信号的非均匀性使得传统的基于傅里叶变换的成像算法不再直接适用。因此,研究出一种适用于非均匀平面阵列的无损检测三维成像算法是非常必要的。后向投影(Back Projection, BP)算法是雷达成像的标准算法,可以适用于各种成像场景。但是BP算法极高的运算复杂度使其在阵元数目较多的情况下需要耗费巨大的计算资源,难以满足成像的时效性需求。距离徙动算法(Range Migration Algorithm, RMA)是一种能兼顾成像质量和速度的雷达成像算法,也是目前在实际场景中被应用最广泛的一种算法。然而RMA中处理非均匀数据的插值步骤往往会带来运算量过大或者精度不够的问题。非均匀快速傅里叶变换(NonUniform Fast Fourier Transform, NUFFT)可以在非均匀空间实现快速傅里叶变换,因此自被提出就展现出了其在雷达成像算法方面的巨大潜力[10-12]。
综上所述,本文针对毫米波非均匀平面阵列,结合RMA和NUFFT的思想,提出了一种适用于无损检测的三维成像算法。通过实验室搭建的毫米波非均匀1D-SISO-1D-scanning成像系统验证了所提算法的有效性。
1 成像模型和算法
毫米波非均匀平面阵列体制下的无损检测成像几何关系如图1所示。阵面上的天线阵元位置为rR=(xR,yR,zR),目标中的缺陷位置为r=(x,y,z)。定义空气部分为区域A,介电常数为εA;目标部分为区域B,介电常数为εB;目标中的缺陷部分为区域C,介电常数为εC。

图1 成像几何模型Fig.1 Imaging geometric model
缺陷区域的散射场可以近似写为:
(1)
其中:k=2πf/c为空间波数,f为发射信号的频率,c为光速;Et(r,rR,k)=jkη0G(r,rR,k)为入射场,η0为自由空间的波阻抗;o(r)=εC(r)-εB(r)为反射率函数;G(rR,r,k)为半空间格林函数。
根据格林函数的性质,可将式(1)改写为:
(2)
其中,半空间格林函数的表达式为:

jkz(zR-z)]F(kx,kz,k)dkxdkz
(3)
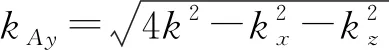
(4)
近场雷达成像主要受相位项的影响,因此将式(3)代入式(2),并忽略幅度项可得:
j(kAyyR-kByy)+jkz(zR-z)]dkxdkzdr
(5)
对式(5)进行关于xR和zR的傅里叶变换可得:
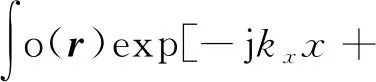
j(kAyyR-kByy)-jkzz]dr
(6)
对式(6)进行相位补偿可得:
exp(-jkByy-jkxx-jkzz)dr
(7)
则待求解的目标函数可以写为:

exp(jkByy+jkxx+jkzz)dkxdkBydkz
(8)
在实际成像过程中,首先考虑到平面阵列是非均匀分布的,故引入NUFFT实现非均匀数据的傅里叶变换:
Er(kx,kz,k)=NUFFTxR,zR[Er(rR,k)]exp(jkAyyR)
(9)
其中,NUFFTxR,zR[·]表示进行关于xR和zR的非均匀快速傅里叶变换。
另外考虑到kx和kz通常均匀分布,其逆傅里叶变换可以直接通过逆快速傅里叶变换(Inverse Fast Fourier Transform, IFFT)实现。 但kBy为非均匀频域数据,RMA处理时会进行插值操作,所提算法通过引入非均匀逆快速傅里叶变换(NonUniform Inverse Fast Fourier Transform, NUIFFT)取代插值和IFFT进行处理:

exp(jkxx+jkzz)dkxdkz]
(10)
其中,NUIFFTkBy[·]表示进行关于kBy的非均匀逆快速傅里叶变换。
因此所提算法的成像公式可总结为:
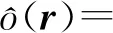
exp(jkAyyR)]]
(11)
其中,IFFTkx,kz[·]表示进行关于kx和kz的逆快速傅里叶变换。
2 成像结果分析
介质目标设置为相对介电常数约为2.008的聚四氟乙烯。设置的非均匀平面阵列排布方式如图2所示,在阵元数为101×101=10 201的均匀平面阵列中通过随机抽样的方式随机抽取掉2 624个阵元,形成共7 577个阵元的非均匀平面阵列。发射信号的中心频率为37.5 GHz,带宽为12 GHz。

图2 非均匀平面阵列构型Fig.2 Nonuniform planar array topology
2.1 仿真结果
首先通过仿真验证所提算法的有效性并进行成像性能的评估。目标设置为一个坐标为(0,0.05,0)m的理想真空点缺陷。分别利用BP算法和所提算法进行成像,得到的结果如图3所示。
由图3可以看到,两种算法均可以对介质中的点目标缺陷进行准确成像。为了定量分析两种算法的性能,以冲激响应宽度(Impulse Response Width, IRW)和峰值旁瓣比(Peak Side Lobe Ratio, PSLR)为精度评价指标、运行时间为速度评价指标进行对比,在相同计算机运行环境下得到的结果如表1所示。

(a) BP算法x-y平面投影(a) x-y plane projection utilizing BP algorithm
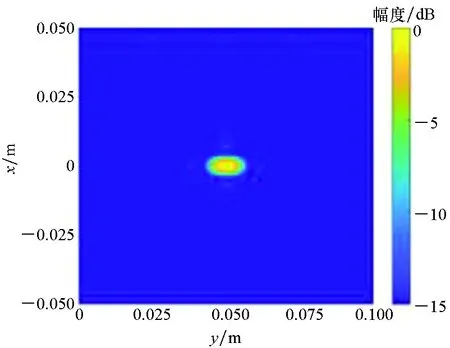
(b) 所提算法x-y平面投影(b) x-y plane projection utilizing the proposed algorithm

(c) BP算法x-z平面投影(c) x-z plane projection utilizing BP algorithm

(d) 所提算法x-z平面投影(d) x-z plane projection utilizing the proposed algorithm

(e) BP算法y-z平面投影(e) y-z plane projection utilizing BP algorithm

(f) 所提算法y-z平面投影(f) y-z plane projection utilizing the proposed algorithm图3 仿真成像结果Fig.3 Simulation imaging results
通过表1的对比可以看到,在三个坐标轴方向上BP算法的IRW都略微小于所提算法的IRW,两者相差不大,说明两种算法的分辨率几乎一致。而在三个坐标轴方向上所提算法的PSLR都小于BP算法的PSLR,说明所提算法的旁瓣抑制效果更好。总的来说,所提算法的成像精度能够与BP算法基本相当。在成像速度方面,所提算法远远快于BP算法。仿真结果有效证明了所提算法的成像效率优势。
2.2 实验结果
在实验室搭建的毫米波非均匀1D-SISO-1D-scanning成像系统中,金属“柠檬片”夹在前后厚度分别为2 cm和0.5 cm的聚四氟乙烯块状材料之间。目标通过泡沫块固定在毫米波非均匀阵列前方。
分别利用BP算法和所提算法进行成像,得到的结果如图4所示。在实验的三维成像结果中,介质目标中的金属“柠檬片”清晰可见,且可以看到聚四氟乙烯块状材料的轮廓。两种算法的成像质量基本相同,但是BP算法得到的成像结果中旁瓣更多,这也与前文对仿真结果的分析一致。
由表1中的运行时间可知,此时BP算法耗费的计算资源仍然是巨大的,而所提算法依旧能够在较短时间内完成成像。

表1 性能比较

(a) BP算法x-y平面投影(a) x-y plane projection utilizing BP algorithm

(b) 所提算法x-y平面投影(b) x-y plane projection utilizing the proposed algorithm

(c) BP算法x-z平面投影(c) x-z plane projection utilizing BP algorithm

(d) 所提算法x-z平面投影(d) x-z plane projection utilizing the proposed algorithm
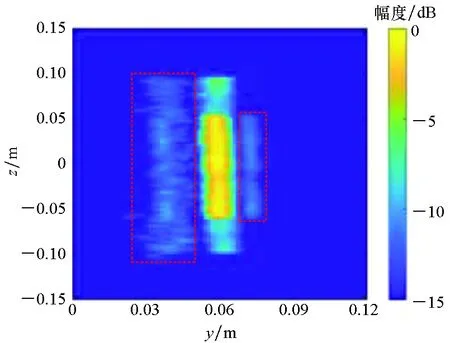
(e) BP算法y-z平面投影(e) y-z plane projection utilizing BP algorithm

(f) 所提算法y-z平面投影(f) y-z plane projection utilizing the proposed algorithm图4 实验成像结果Fig.4 Experimental imaging results
3 结论
本文提出了一种毫米波非均匀平面阵列无损检测三维成像算法,解决了传统基于傅里叶变换的成像算法不能适用于非均匀信号和算法中插值操作难以兼顾精度与速度的问题。仿真中,利用理想点缺陷目标定量分析了两种算法的成像性能。同时利用搭建的毫米波非均匀1D-SISO-1D-scanning成像系统进行了实验。结果表明,相较于BP算法,所提算法能够实现相当的成像精度,同时在成像速度方面具有明显优势。本文工作可为未来毫米波成像技术在无损检测领域的发展提供思路和支持。
